第二章 §2.4 2.4.1圆的标准方程 课件(共57张PPT)
文档属性
| 名称 | 第二章 §2.4 2.4.1圆的标准方程 课件(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 21:40:49 | ||
图片预览











文档简介
(共57张PPT)
2.4.1 圆的标准方程
第二章 §2.4 圆的方程
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的位置关系.
学习目标
《古朗月行》
唐 李白
小时不识月,呼作白玉盘。
又疑瑶台镜,飞在青云端。
月亮,是中国人心目中的宇宙精灵,古代的人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写,如果把天空看作一个平面,月亮当作一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示?
导语
随堂演练
课时对点练
一、圆的标准方程
二、点与圆的位置关系
三、待定系数法求圆的标准方程
内容索引
一、圆的标准方程
问题1 圆是怎样定义的?确定它的要素又是什么呢?各要素与圆有怎样的关系?
提示 平面内到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径.
确定圆的因素:圆心和半径,
圆心确定圆的位置,半径确定圆的大小.
问题2 已知圆心为A(a,b),半径为r,你能推导出圆的方程吗?
提示 设圆上任一点M(x,y),
则|MA|=r,由两点间的距离公式,
化简可得:(x-a)2+(y-b)2=r2.
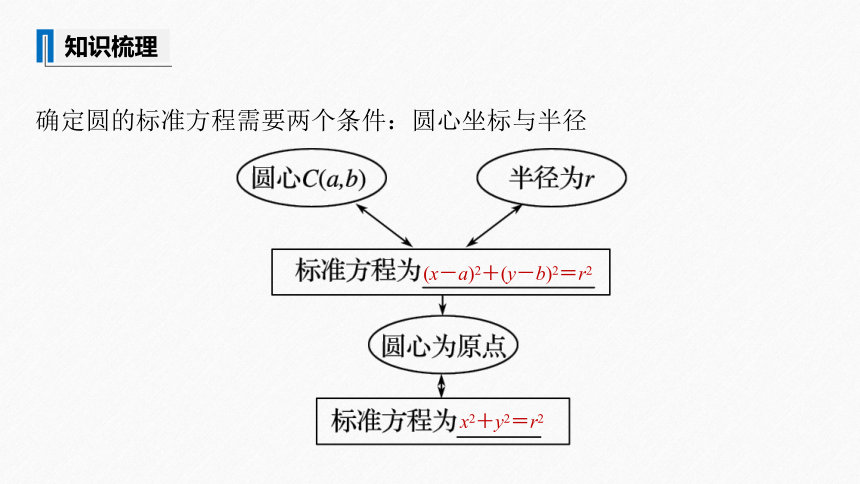
确定圆的标准方程需要两个条件:圆心坐标与半径
(x-a)2+(y-b)2=r2
知识梳理
x2+y2=r2
注意点:
(1)当圆心在原点即A(0,0),半径长r=1时,方程为x2+y2=1,称为单位圆.
(2)相同的圆,建立坐标系不同时,圆心坐标不同,导致圆的方程不同,但是半径是不变的.
(3)圆上的点都满足方程,满足方程的点都在圆上.
例1 (1)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为___________________.
解析 ∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
(x+5)2+(y+3)2=25
(2)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程是__________
___________.
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
(x-1)2+
(y-2)2=25
∴该圆的标准方程为(x-1)2+(y-2)2=25.
反思感悟 直接法求圆的标准方程的策略
确定圆的标准方程只需确定圆心坐标和半径,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.
跟踪训练1 求满足下列条件的圆的标准方程:
(1)圆心是(4,0),且过点(2,2);
解 r2=(2-4)2+(2-0)2=8,
∴圆的标准方程为(x-4)2+y2=8.
(2)圆心在y轴上,半径为5,且过点(3,-4).
解 设圆心为C(0,b),则(3-0)2+(-4-b)2=52,
∴b=0或b=-8,∴圆心为(0,0)或(0,-8),
又r=5,
∴圆的标准方程为x2+y2=25或x2+(y+8)2=25.
二、点与圆的位置关系
问题3 点M0(x0,y0)在圆x2+y2=r2内的条件是什么?在圆x2+y2=r2外的条件又是什么?
提示 点在圆内时,点到圆心的距离小于半径,点在圆外时,点到圆心的距离大于半径.
位置关系 利用距离判断 利用方程判断
点在圆外 d r (x0-a)2+(y0-b)2 r2
点在圆上 d r (x0-a)2+(y0-b)2 r2
点在圆内 d r (x0-a)2+(y0-b)2 r2
圆C:(x-a)2+(y-b)2=r2(r>0),其圆心为C(a,b),半径为r,点P(x0,y0),
>
>
知识梳理
=
=
<
<
例2 (1)已知a,b是方程x2-x- =0的两个不相等的实数根,则点P(a,b)与圆C:x2+y2=8的位置关系是
A.点P在圆C内 B.点P在圆C外
C.点P在圆C上 D.无法确定
√
∴点P在圆C内.
(2)已知点P(2,1)和圆C: +(y-1)2=1,若点P在圆C上,则实数a=
_________.若点P在圆C外,则实数a的取值范围为_______________.
-2或-6
a<-6或a>-2
解得a=-2或-6.
解得a<-6或a>-2.
反思感悟 判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:把点的坐标代入圆的标准方程,判断式子两边的大小,并作出判断.
[0,1)
三、待定系数法求圆的标准方程
例3 求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
解 方法一 (待定系数法)
设圆的标准方程为(x-a)2+(y-b)2=r2,
即圆的标准方程是(x-4)2+(y+3)2=25.
方法二 (几何法)
由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
∵弦的垂直平分线过圆心,
即圆心坐标为(4,-3),
即圆的标准方程是(x-4)2+(y+3)2=25.
反思感悟 待定系数法求圆的标准方程的一般步骤
跟踪训练3 过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是
A.(x-3)2+(y+1)2=4 B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4 D.(x+1)2+(y+1)2=4
√
所以线段AB的垂直平分线的方程为y=x.
所以圆心坐标为(1,1),半径为2,
所以所求圆的方程为(x-1)2+(y-1)2=4.
方法二 本题作为选择题,可采用排除法,根据圆心在直线x+y-2=0上,排除B,D;
根据点B(-1,1)在圆上,排除A.
1.知识清单:
(1)圆的标准方程.
(2)点和圆的位置关系.
2.方法归纳:直接法、几何法、待定系数法.
3.常见误区:几何法求圆的方程出现漏解情况.
课堂小结
随堂演练
1.以(2,-1)为圆心,4为半径的圆的方程为
A.(x+2)2+(y-1)2=4 B.(x+2)2+(y+1)2=4
C.(x-2)2+(y+1)2=16 D.(x+2)2+(y-1)2=16
√
1
2
3
4
解析 以(2,-1)为圆心,4为半径的圆的方程为(x-2)2+(y+1)2=16.
2.点P(1,3)与圆x2+y2=24的位置关系是
A.在圆外 B.在圆内
C.在圆上 D.不确定
√
1
2
3
4
3.圆心在y轴上,半径为1,且过点(1,2)的圆的标准方程是
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
√
1
2
3
4
解析 方法一 (直接法)
∴b=2,∴圆的标准方程是x2+(y-2)2=1.
方法二 (数形结合法)
作图(如图),根据点(1,2)到圆心的距离为1,易知圆心为(0,2),
故圆的标准方程是x2+(y-2)2=1.
4.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为
_______________.
1
2
3
4
解析 ∵P在圆外,
∴(5a+1-1)2+(12a)2>1,169a2>1,
课时对点练
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知点A(3,-2),B(-5,4),以线段AB为直径的圆的标准方程是
A.(x-1)2+(y+1)2=25
B.(x+1)2+(y-1)2=25
C.(x-1)2+(y+1)2=100
D.(x+1)2+(y-1)2=100
√
所以圆的标准方程是(x+1)2+(y-1)2=25.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 圆(x-1)2+y2=1的圆心坐标为(1,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知圆(x-a)2+(y-1)2=2a(0<a<1),则原点O在
A.圆内 B.圆外
C.圆上 D.圆上或圆外
√
解析 由圆的方程(x-a)2+(y-1)2=2a,知圆心为(a,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)已知圆M:(x-4)2+(y+3)2=25,则下列说法正确的是
A.圆M的圆心为(4,-3)
B.圆M的圆心为(-4,3)
C.圆M的半径为5
D.圆M被y轴截得的线段长为6
√
解析 由圆M:(x-4)2+(y+3)2=52,
故圆心为(4,-3),半径为5,则AC正确;
令x=0,得y=0或y=-6,线段长为6,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
6.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为
A.(x+2)2+(y-2)2=1 B.(x-2)2+(y+2)2=1
C.(x+2)2+(y+2)2=1 D.(x-2)2+(y-2)2=1
√
解析 在圆C2上任取一点(x,y),
则此点关于直线x-y-1=0的对称点(y+1,x-1)在圆C1:(x+1)2+(y-1)2=1上,
所以(y+1+1)2+(x-1-1)2=1,
即(x-2)2+(y+2)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.与圆C:(x-1)2+y2=36同圆心,且面积等于圆C面积的一半的圆的方程为________________.
(x-1)2+y2=18
解析 圆C的半径R=6,设所求圆的半径为r,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又圆心坐标为(1,0),则圆的方程为(x-1)2+y2=18.
8.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是________.
解析 圆(x-1)2+(y-1)2=1的圆心为C(1,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆N上,求半径a;
解 ∵点M(6,9)在圆N上,
∴(6-5)2+(9-6)2=a2,∴a2=10.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若点P(3,3)与Q(5,3)有一点在圆内,另一点在圆外,求a的取值范围.
解 由已知,得圆心N(5,6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴|PN|>|QN|,故点P在圆外,点Q在圆内,
10.已知点A(1,-2),B(-1,4),求
(1)过点A,B且周长最小的圆的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当AB为直径时,过A,B的圆的半径最小,从而周长最小.
则圆的方程为x2+(y-1)2=10.
(2)过点A,B且圆心在直线2x-y-4=0上的圆的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即x-3y+3=0,
由圆心在直线2x-y-4=0上,得两直线交点为圆心,即圆心坐标是C(3,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故所求圆的方程是(x-3)2+(y-2)2=20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 待定系数法
设圆的方程为(x-a)2+(y-b)2=r2.
故所求圆的方程为(x-3)2+(y-2)2=20.
11.(多选)以直线2x+y-4=0与两坐标轴的一个交点为圆心,过另一个交点的圆的方程可能为
A.x2+(y-4)2=20 B.(x-4)2+y2=20
C.x2+(y-2)2=20 D.(x-2)2+y2=20
√
解析 令x=0,则y=4;令y=0,则x=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
过B点的圆的方程为x2+(y-4)2=20.
以B为圆心,过A点的圆的方程为(x-2)2+y2=20.
√
12.已知直线(3+2λ)x+(3λ-2)y+5-λ=0恒过定点P,则与圆C:(x-2)2+(y+3)2=16有公共的圆心且过点P的圆的标准方程为
A.(x-2)2+(y+3)2=36
B.(x-2)2+(y+3)2=25
C.(x-2)2+(y+3)2=18
D.(x-2)2+(y+3)2=9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由(3+2λ)x+(3λ-2)y+5-λ=0,
得(2x+3y-1)λ+(3x-2y+5)=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵圆C:(x-2)2+(y+3)2=16的圆心坐标是(2,-3),
∴所求圆的标准方程为(x-2)2+(y+3)2=25,故选B.
13.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是________________.
(x-4)2+y2=1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设圆心A(3,-1)关于直线x+y-3=0对称的点B的坐标为(a,b),
故所求圆的标准方程为(x-4)2+y2=1.
14.已知点P(x,y)为圆x2+y2=1上的动点,则x2-4y的最小值为_____.
解析 ∵点P(x,y)为圆x2+y2=1上的动点,
∴x2-4y=1-y2-4y=-(y+2)2+5.
∵y∈[-1,1],
∴当y=1时,-(y+2)2+5有最小值-4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-4
15.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为
A.4 B.5 C.6 D.7
所以|OC|≥5-1=4,当且仅当C在线段OM上时取等号.
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简得(x-3)2+(y-4)2=1,
所以圆心C的轨迹是以M(3,4)为圆心,1为半径的圆,
16.设圆满足:①截y轴所得弦长为2;②被x轴分成两段弧,其弧长比为3∶1.在满足上述条件的圆中,求圆心到直线l:x-2y=0的距离最小时的圆的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设圆心为(a,b),半径长为r,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
消去r,得2b2-a2=1, ①
设a-2b=k,则a=2b+k,代入①式,
整理得2b2+4bk+k2+1=0.
判别式Δ=8(k2-1)≥0,解得|k|≥1,
当k=1时,a=b=-1,圆的方程为(x+1)2+(y+1)2=2;
当k=-1时,a=b=1,圆的方程为(x-1)2+(y-1)2=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.4.1 圆的标准方程
第二章 §2.4 圆的方程
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的位置关系.
学习目标
《古朗月行》
唐 李白
小时不识月,呼作白玉盘。
又疑瑶台镜,飞在青云端。
月亮,是中国人心目中的宇宙精灵,古代的人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写,如果把天空看作一个平面,月亮当作一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示?
导语
随堂演练
课时对点练
一、圆的标准方程
二、点与圆的位置关系
三、待定系数法求圆的标准方程
内容索引
一、圆的标准方程
问题1 圆是怎样定义的?确定它的要素又是什么呢?各要素与圆有怎样的关系?
提示 平面内到定点的距离等于定长的点的集合叫做圆,定点称为圆心,定长称为圆的半径.
确定圆的因素:圆心和半径,
圆心确定圆的位置,半径确定圆的大小.
问题2 已知圆心为A(a,b),半径为r,你能推导出圆的方程吗?
提示 设圆上任一点M(x,y),
则|MA|=r,由两点间的距离公式,
化简可得:(x-a)2+(y-b)2=r2.
确定圆的标准方程需要两个条件:圆心坐标与半径
(x-a)2+(y-b)2=r2
知识梳理
x2+y2=r2
注意点:
(1)当圆心在原点即A(0,0),半径长r=1时,方程为x2+y2=1,称为单位圆.
(2)相同的圆,建立坐标系不同时,圆心坐标不同,导致圆的方程不同,但是半径是不变的.
(3)圆上的点都满足方程,满足方程的点都在圆上.
例1 (1)与y轴相切,且圆心坐标为(-5,-3)的圆的标准方程为___________________.
解析 ∵圆心坐标为(-5,-3),又与y轴相切,
∴该圆的半径为5,
∴该圆的标准方程为(x+5)2+(y+3)2=25.
(x+5)2+(y+3)2=25
(2)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程是__________
___________.
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
(x-1)2+
(y-2)2=25
∴该圆的标准方程为(x-1)2+(y-2)2=25.
反思感悟 直接法求圆的标准方程的策略
确定圆的标准方程只需确定圆心坐标和半径,常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.
跟踪训练1 求满足下列条件的圆的标准方程:
(1)圆心是(4,0),且过点(2,2);
解 r2=(2-4)2+(2-0)2=8,
∴圆的标准方程为(x-4)2+y2=8.
(2)圆心在y轴上,半径为5,且过点(3,-4).
解 设圆心为C(0,b),则(3-0)2+(-4-b)2=52,
∴b=0或b=-8,∴圆心为(0,0)或(0,-8),
又r=5,
∴圆的标准方程为x2+y2=25或x2+(y+8)2=25.
二、点与圆的位置关系
问题3 点M0(x0,y0)在圆x2+y2=r2内的条件是什么?在圆x2+y2=r2外的条件又是什么?
提示 点在圆内时,点到圆心的距离小于半径,点在圆外时,点到圆心的距离大于半径.
位置关系 利用距离判断 利用方程判断
点在圆外 d r (x0-a)2+(y0-b)2 r2
点在圆上 d r (x0-a)2+(y0-b)2 r2
点在圆内 d r (x0-a)2+(y0-b)2 r2
圆C:(x-a)2+(y-b)2=r2(r>0),其圆心为C(a,b),半径为r,点P(x0,y0),
>
>
知识梳理
=
=
<
<
例2 (1)已知a,b是方程x2-x- =0的两个不相等的实数根,则点P(a,b)与圆C:x2+y2=8的位置关系是
A.点P在圆C内 B.点P在圆C外
C.点P在圆C上 D.无法确定
√
∴点P在圆C内.
(2)已知点P(2,1)和圆C: +(y-1)2=1,若点P在圆C上,则实数a=
_________.若点P在圆C外,则实数a的取值范围为_______________.
-2或-6
a<-6或a>-2
解得a=-2或-6.
解得a<-6或a>-2.
反思感悟 判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:把点的坐标代入圆的标准方程,判断式子两边的大小,并作出判断.
[0,1)
三、待定系数法求圆的标准方程
例3 求经过点P(1,1)和坐标原点,并且圆心在直线2x+3y+1=0上的圆的标准方程.
解 方法一 (待定系数法)
设圆的标准方程为(x-a)2+(y-b)2=r2,
即圆的标准方程是(x-4)2+(y+3)2=25.
方法二 (几何法)
由题意知OP是圆的弦,其垂直平分线为x+y-1=0.
∵弦的垂直平分线过圆心,
即圆心坐标为(4,-3),
即圆的标准方程是(x-4)2+(y+3)2=25.
反思感悟 待定系数法求圆的标准方程的一般步骤
跟踪训练3 过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的方程是
A.(x-3)2+(y+1)2=4 B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4 D.(x+1)2+(y+1)2=4
√
所以线段AB的垂直平分线的方程为y=x.
所以圆心坐标为(1,1),半径为2,
所以所求圆的方程为(x-1)2+(y-1)2=4.
方法二 本题作为选择题,可采用排除法,根据圆心在直线x+y-2=0上,排除B,D;
根据点B(-1,1)在圆上,排除A.
1.知识清单:
(1)圆的标准方程.
(2)点和圆的位置关系.
2.方法归纳:直接法、几何法、待定系数法.
3.常见误区:几何法求圆的方程出现漏解情况.
课堂小结
随堂演练
1.以(2,-1)为圆心,4为半径的圆的方程为
A.(x+2)2+(y-1)2=4 B.(x+2)2+(y+1)2=4
C.(x-2)2+(y+1)2=16 D.(x+2)2+(y-1)2=16
√
1
2
3
4
解析 以(2,-1)为圆心,4为半径的圆的方程为(x-2)2+(y+1)2=16.
2.点P(1,3)与圆x2+y2=24的位置关系是
A.在圆外 B.在圆内
C.在圆上 D.不确定
√
1
2
3
4
3.圆心在y轴上,半径为1,且过点(1,2)的圆的标准方程是
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
√
1
2
3
4
解析 方法一 (直接法)
∴b=2,∴圆的标准方程是x2+(y-2)2=1.
方法二 (数形结合法)
作图(如图),根据点(1,2)到圆心的距离为1,易知圆心为(0,2),
故圆的标准方程是x2+(y-2)2=1.
4.若点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为
_______________.
1
2
3
4
解析 ∵P在圆外,
∴(5a+1-1)2+(12a)2>1,169a2>1,
课时对点练
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知点A(3,-2),B(-5,4),以线段AB为直径的圆的标准方程是
A.(x-1)2+(y+1)2=25
B.(x+1)2+(y-1)2=25
C.(x-1)2+(y+1)2=100
D.(x+1)2+(y-1)2=100
√
所以圆的标准方程是(x+1)2+(y-1)2=25.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 圆(x-1)2+y2=1的圆心坐标为(1,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知圆(x-a)2+(y-1)2=2a(0<a<1),则原点O在
A.圆内 B.圆外
C.圆上 D.圆上或圆外
√
解析 由圆的方程(x-a)2+(y-1)2=2a,知圆心为(a,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.(多选)已知圆M:(x-4)2+(y+3)2=25,则下列说法正确的是
A.圆M的圆心为(4,-3)
B.圆M的圆心为(-4,3)
C.圆M的半径为5
D.圆M被y轴截得的线段长为6
√
解析 由圆M:(x-4)2+(y+3)2=52,
故圆心为(4,-3),半径为5,则AC正确;
令x=0,得y=0或y=-6,线段长为6,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
6.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为
A.(x+2)2+(y-2)2=1 B.(x-2)2+(y+2)2=1
C.(x+2)2+(y+2)2=1 D.(x-2)2+(y-2)2=1
√
解析 在圆C2上任取一点(x,y),
则此点关于直线x-y-1=0的对称点(y+1,x-1)在圆C1:(x+1)2+(y-1)2=1上,
所以(y+1+1)2+(x-1-1)2=1,
即(x-2)2+(y+2)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.与圆C:(x-1)2+y2=36同圆心,且面积等于圆C面积的一半的圆的方程为________________.
(x-1)2+y2=18
解析 圆C的半径R=6,设所求圆的半径为r,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又圆心坐标为(1,0),则圆的方程为(x-1)2+y2=18.
8.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是________.
解析 圆(x-1)2+(y-1)2=1的圆心为C(1,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知圆N的标准方程为(x-5)2+(y-6)2=a2(a>0).
(1)若点M(6,9)在圆N上,求半径a;
解 ∵点M(6,9)在圆N上,
∴(6-5)2+(9-6)2=a2,∴a2=10.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若点P(3,3)与Q(5,3)有一点在圆内,另一点在圆外,求a的取值范围.
解 由已知,得圆心N(5,6).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴|PN|>|QN|,故点P在圆外,点Q在圆内,
10.已知点A(1,-2),B(-1,4),求
(1)过点A,B且周长最小的圆的方程;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当AB为直径时,过A,B的圆的半径最小,从而周长最小.
则圆的方程为x2+(y-1)2=10.
(2)过点A,B且圆心在直线2x-y-4=0上的圆的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即x-3y+3=0,
由圆心在直线2x-y-4=0上,得两直线交点为圆心,即圆心坐标是C(3,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故所求圆的方程是(x-3)2+(y-2)2=20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 待定系数法
设圆的方程为(x-a)2+(y-b)2=r2.
故所求圆的方程为(x-3)2+(y-2)2=20.
11.(多选)以直线2x+y-4=0与两坐标轴的一个交点为圆心,过另一个交点的圆的方程可能为
A.x2+(y-4)2=20 B.(x-4)2+y2=20
C.x2+(y-2)2=20 D.(x-2)2+y2=20
√
解析 令x=0,则y=4;令y=0,则x=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
过B点的圆的方程为x2+(y-4)2=20.
以B为圆心,过A点的圆的方程为(x-2)2+y2=20.
√
12.已知直线(3+2λ)x+(3λ-2)y+5-λ=0恒过定点P,则与圆C:(x-2)2+(y+3)2=16有公共的圆心且过点P的圆的标准方程为
A.(x-2)2+(y+3)2=36
B.(x-2)2+(y+3)2=25
C.(x-2)2+(y+3)2=18
D.(x-2)2+(y+3)2=9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由(3+2λ)x+(3λ-2)y+5-λ=0,
得(2x+3y-1)λ+(3x-2y+5)=0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵圆C:(x-2)2+(y+3)2=16的圆心坐标是(2,-3),
∴所求圆的标准方程为(x-2)2+(y+3)2=25,故选B.
13.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是________________.
(x-4)2+y2=1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设圆心A(3,-1)关于直线x+y-3=0对称的点B的坐标为(a,b),
故所求圆的标准方程为(x-4)2+y2=1.
14.已知点P(x,y)为圆x2+y2=1上的动点,则x2-4y的最小值为_____.
解析 ∵点P(x,y)为圆x2+y2=1上的动点,
∴x2-4y=1-y2-4y=-(y+2)2+5.
∵y∈[-1,1],
∴当y=1时,-(y+2)2+5有最小值-4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-4
15.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为
A.4 B.5 C.6 D.7
所以|OC|≥5-1=4,当且仅当C在线段OM上时取等号.
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简得(x-3)2+(y-4)2=1,
所以圆心C的轨迹是以M(3,4)为圆心,1为半径的圆,
16.设圆满足:①截y轴所得弦长为2;②被x轴分成两段弧,其弧长比为3∶1.在满足上述条件的圆中,求圆心到直线l:x-2y=0的距离最小时的圆的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 设圆心为(a,b),半径长为r,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
消去r,得2b2-a2=1, ①
设a-2b=k,则a=2b+k,代入①式,
整理得2b2+4bk+k2+1=0.
判别式Δ=8(k2-1)≥0,解得|k|≥1,
当k=1时,a=b=-1,圆的方程为(x+1)2+(y+1)2=2;
当k=-1时,a=b=1,圆的方程为(x-1)2+(y-1)2=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
