第三章 §3.3 3.3.1抛物线及其标准方程 课件(共62张PPT)
文档属性
| 名称 | 第三章 §3.3 3.3.1抛物线及其标准方程 课件(共62张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 21:52:48 | ||
图片预览











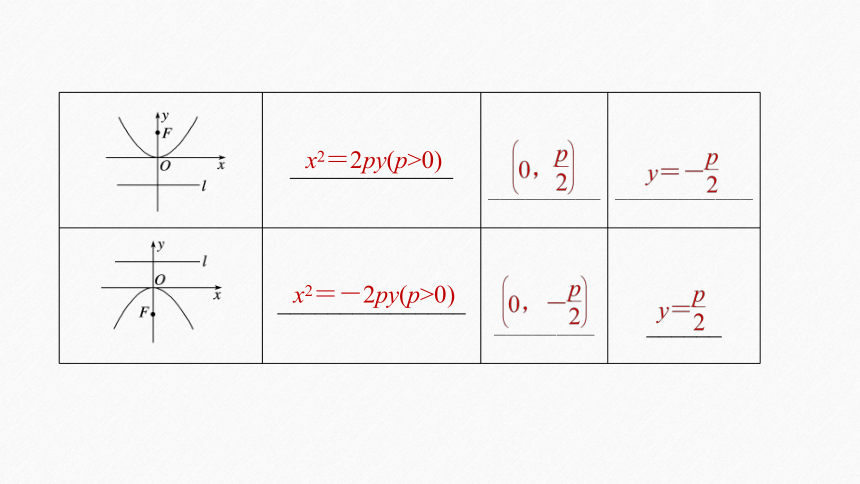
文档简介
(共62张PPT)
3.3.1 抛物线及其标准方程
第三章 §3.3 抛物线
1.掌握抛物线的定义及其焦点、准线的概念.
2.会求简单的抛物线方程.
学习目标
通过前面的学习可以发现,如果动点M到定点F的距离与M到定直线l(不过点F)的距离之比为k,当01时,点M的轨迹为双曲线.一个自然的问题是:当k=1时,即动点M到定点F的距离与它到定直线l的距离相等时,点M的轨迹会是什么形状?
导语
随堂演练
课时对点练
一、抛物线的定义
二、抛物线定义的应用
三、抛物线的实际应用问题
内容索引
一、抛物线的定义
问题1 利用信息技术作图,如图所示,F是定点,l是不经过点F的定直线,H是直线l上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,点M随之运动,你能发现点M满足的几何条件吗?它的轨迹是什么形状?
提示 点M随着点H运动的过程中,始终有|MF|=|MH|,即点M与定点F的距离等于它到定直线l的距离,点M的轨迹形状与二次函数的图象相似.
1.定义:平面内与一个定点F和一条定直线l(不经过点F)的 的点的轨迹叫做抛物线.
2.焦点:定点 .
3.准线:定直线 .
注意点:
(1)“一动三定”:一动点M;一定点F(即焦点);一定直线l(即准线);一定值1(即动点M到定点F的距离与到定直线l的距离之比为1).
(2)若点F在直线l上,点的轨迹是过点F且垂直于直线l的直线.
距离相等
F
知识梳理
l
问题2 比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,可能使所求抛物线的方程形式简单?
提示 我们取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合,建立平面直角坐标系Oxy.
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M||MF|=d}.
将上式两边平方并化简,得y2=2px(p>0).
图形 标准方程 焦点坐标 准线方程
_____________ _________
__________
_______________ ________
__________
y2=2px(p>0)
知识梳理
y2=-2px(p>0)
_____________ _________
___________
_______________ ________
______
x2=2py(p>0)
x2=-2py(p>0)
注意点:
(1)p的几何意义是焦点到准线的距离.
(2)标准方程的结构特征:顶点在坐标原点、焦点在坐标轴上.
(3)抛物线的开口方向:抛物线的开口方向取决于一次项变量(x或y)的取值范围.
例1 分别求符合下列条件的抛物线的标准方程.
(1)经过点(-3,-1);
解 因为点(-3,-1)在第三象限,
所以设所求抛物线的标准方程为y2=-2px(p>0)或x2=-2py(p>0).
若抛物线的标准方程为y2=-2px(p>0),
若抛物线的标准方程为x2=-2py(p>0),
(2)焦点为直线3x-4y-12=0与坐标轴的交点.
解 对于直线方程3x-4y-12=0,
令x=0,得y=-3;令y=0,得x=4,
所以抛物线的焦点为(0,-3)或(4,0).
此时抛物线的标准方程为x2=-12y;
此时抛物线的标准方程为y2=16x.
故所求抛物线的标准方程为x2=-12y或y2=16x.
反思感悟 用待定系数法求抛物线标准方程的步骤
注意:当抛物线的类型没有确定时,可设方程为y2=mx(m≠0)或x2=ny(n≠0),这样可以减少讨论情况的个数.
跟踪训练1 (1)若抛物线y2=2px(p>0)的焦点坐标为(1,0),则p=_____,准线方程为________.
2
x=-1
解析 因为抛物线的焦点坐标为(1,0),
(2)焦点在y轴上,焦点到准线的距离为5的抛物线的标准方程为________
____________.
解析 设方程为x2=2my(m≠0),
由焦点到准线的距离为5,
知|m|=5,m=±5,
所以满足条件的抛物线有两条,它们的标准方程分别为x2=10y和x2=
-10y.
x2=10y
和x2=-10y
二、抛物线定义的应用
例2 (1)已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=
则x0等于
A.1 B.2 C.4 D.8
√
∴x0=1.
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
解 由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.
延伸探究
1.若将本例(2)中的点(0,2)改为点A(3,2),求|PA|+|PF|的最小值.
解 将x=3代入y2=2x,
所以点A在抛物线内部.
则|PA|+|PF|=|PA|+d.
解 如图,作PQ垂直于准线l于点Q,
|PA1|+|PQ|=|PA1|+|PF|≥|A1F|min.
即所求最小值为1.
反思感悟 抛物线定义的应用
实现距离转化.根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距与点线距的相互转化,从而简化某些问题.
跟踪训练2 (1)已知抛物线y2=2px(p>0)的焦点F1,若点A(2,-4)在抛物线上,则点A到焦点的距离为_____.
解析 把点(2,-4)代入抛物线y2=2px,得16=4p,
即p=4,从而抛物线的焦点为(2,0).
故点A到焦点的距离为4.
4
(2)设点A的坐标为(1, ),点P在抛物线y2=8x上移动,P到直线x=-1的距离为d,则d+|PA|的最小值为
A.1 B.2 C.3 D.4
√
解析 由题意知抛物线y2=8x的焦点为F(2,0),点P到准线x=-2的距离为d+1,于是|PF|=d+1,
所以d+|PA|=|PF|-1+|PA|的最小值为|AF|-1=4-1=3.
三、抛物线的实际应用问题
例3 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
解 如图,以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,
建立平面直角坐标系.设抛物线方程为x2=-2py(p>0),
由题意可知,点B(4,-5)在抛物线上,
当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA′,
又知船面露出水面上的部分高为0.75 m,所以h=|yA|+0.75=2(m).
所以水面上涨到与抛物线形拱桥拱顶相距2 m时,小船开始不能通航.
反思感悟 涉及拱桥、隧道的问题,通常需建立适当的平面直角坐标系,利用抛物线的标准方程进行求解.
跟踪训练3 某桥的桥形可近似地看成抛物线,该桥的高度为h,跨径为a,则桥形对应的抛物线的焦点到准线的距离为
√
解析 如图所示,以桥顶为坐标原点,桥形的对称轴为y轴建立平面直角坐标系Oxy.设抛物线为x2=-2py(p>0),
1.知识清单:
(1)抛物线的定义.
(2)抛物线的标准方程的四种形式.
(3)抛物线定义的应用.
2.方法归纳:待定系数法、定义法、转化化归.
3.常见误区:混淆抛物线的焦点位置和方程形式.
课堂小结
随堂演练
由此可知准线方程为y=2.
√
1
2
3
4
2.已知抛物线y=2px2过点(1,4),则该抛物线的焦点坐标为
√
1
2
3
4
解析 由抛物线y=2px2过点(1,4),可得p=2,
∴右顶点的坐标为(4,0).
设抛物线的标准方程为y2=2px(p>0),
1
2
3
4
y2=16x
∴抛物线的标准方程为y2=16x.
4.若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,则点M的坐标为____________________.
(-9,6)或(-9,-6)
1
2
3
4
解析 由抛物线方程y2=-2px(p>0),
设点M到准线的距离为d,
得p=2,故抛物线方程为y2=-4x.
由点M(-9,y)在抛物线上,得y=±6,
故点M的坐标为(-9,6)或(-9,-6).
课时对点练
1.准线与x轴垂直,且经过点(1,- )的抛物线的标准方程是
A.y2=-2x B.y2=2x
C.x2=2y D.x2=-2y
√
解析 由题意可设抛物线的标准方程为y2=2px(p> 0),
则(- )2=2p,
解得p=1,因此抛物线的标准方程为y2=2x.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)经过点P(4,-2)的抛物线的标准方程可以为
A.y2=x B.x2=8y
C.x2=-8y D.y2=-8x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 若抛物线的焦点在x轴上,
设抛物线的方程为y2=2px(p>0),
又因为抛物线经过点P(4,-2),
所以(-2)2=2p×4,
解得p= ,
所以抛物线的方程为y2=x.
若抛物线的焦点在y轴上,设抛物线的方程为x2=-2py(p>0),
又因为抛物线经过点P(4,-2),
所以42=-2p×(-2),解得p=4,所以抛物线的方程为x2=-8y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.过点A(3,0)且与y轴相切的圆的圆心轨迹为
A.圆 B.椭圆
C.直线 D.抛物线
√
解析 由题意可知,
动圆的圆心到点A的距离与到y轴的距离相等,满足抛物线的定义,
故应选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知抛物线的顶点在原点,对称轴为x轴,焦点在双曲线 上,则抛物线的方程为
A.y2=8x B.y2=4x
C.y2=2x D.y2=±8x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即为(-2,0)或(2,0),
所以抛物线的方程为y2=8x或y2=-8x.
5.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是
√
解析 易知直线l2:x=-1恰为抛物线y2=4x的准线,
如图所示,动点P到l2:x=-1的距离可转化为PF的长度,
其中F(1,0)为抛物线y2=4x的焦点.由图可知,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.为响应国家“节能减排,开发清洁能源”的号召,小华制作了一个太阳灶,如图所示.集光板由抛物面(抛物线绕对称轴旋转得到)形的反光镜构成,已知镜口圆的直径为2 m,镜深0.25 m,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.0.5 m B.1 m C.1.5 m D.2 m
√
解析 若使吸收太阳光的效果最好,容器灶圈应在抛物面对应轴截面的抛物线的焦点处,
如图,画出抛物面的轴截面,并建立坐标系,
设抛物线方程为x2=2py(p>0),集光板端点A(1,0.25) ,
代入抛物线方程可得2×0.25p=1,p=2,
所以抛物线方程为x2=4y,故焦点坐标是F(0,1).
所以容器灶圈应距离集光板顶点1 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵抛物线y2=8x的准线方程为x=-2,
该双曲线的一个焦点在抛物线y2=8x的准线上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴a2+b2=4, ②
由①②,得a2=3,b2=1,
8.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上的一点,PA⊥l,A为垂足,如果直线AF的斜率为- 那么|PF|=___.
8
解析 如图,∠AFE=60°,
因为F(2,0),
所以E(-2,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故|PF|=|PA|=6+2=8.
9.根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴p=6,∴抛物线的方程为y2=-12x.
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解 设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又(-3)2=2pm,
∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
10.已知抛物线C:x2=2py(p>0)上两点A,B且AB⊥y轴,OA⊥OB,△AOB的面积为16,求抛物线C的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 不妨设点A在第一象限且A(m,n),
则B(-m,n),可得m2=2pn,
AB⊥y轴,且OA⊥OB,
即△AOB为等腰直角三角形,
则OA的斜率为1,即m=n,
解得m=n=4,p=2,所以抛物线C的方程为x2=4y.
√
解析 由题意知,A为抛物线的焦点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
则|PA|+|PB|=d+|PB|,d+|PB|的最小值为B到准线的距离,
当PB垂直于准线时取最小值.
√
解析 过点Q作QQ′⊥l于点Q′,如图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴|PQ|∶|PF|=3∶4,
又焦点F到准线l的距离为4,
∴|QF|=|QQ′|=3.
6
解析 设A(x1,y1),B(x2,y2),C(x3,y3),又F(1,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即x1+x2+x3=3,
14.对标准形式的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).
其中满足抛物线方程为y2=10x的是________.(要求填写适合条件的序号)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②④
解析 抛物线y2=10x的焦点在x轴上,②满足,①不满足;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若由原点向该直线作垂线,垂足为(2,1)时,
则k=-2,此时存在,
所以④满足.
15.已知P为抛物线x2=12y上一个动点,Q为圆(x-4)2+y2=1上一个动点,则点P到点Q的距离与点P到x轴距离之和的最小值是
A.4 B.3
C.2 D.1
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由抛物线的方程可知焦点F(0,3),则准线方程为y=-3,
如图,过点P作x轴的垂线,垂足为点A,延长PA交准线于点B,设圆(x-4)2+y2=1的圆心为点C.
根据抛物线的定义可得|PA|=|PB|-|AB|=|PF|-|AB|,
∴|PA|+|PQ|=|PF|+|PQ|-|AB|=|PF|+|PQ|-3,
∴当|PA|+|PQ|最小时,则|PF|+|PQ|最小,即F,P,Q(Q位于C,P之间)三点共线时,|PA|+|PQ|最小,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴(|PA|+|PQ|)min=(|PF|+|PQ|)min-3=4-3=1.
16.设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.
(1)若点P到直线x=-1的距离为d,A(-1,1),求|PA|+d的最小值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 依题意,抛物线的焦点为F(1,0),准线方程为x=-1.
由抛物线的定义,知|PF|=d,
于是问题转化为求|PA|+|PF|的最小值.
如图,连接AF,交抛物线于点P,
(2)若B(3,2),求|PB|+|PF|的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
过点B作BQ垂直于准线于点Q,交抛物线于点P1(如图).
由抛物线的定义,知|P1Q|=|P1F|,
则|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=3+1=4.
即|PB|+|PF|的最小值为4.
3.3.1 抛物线及其标准方程
第三章 §3.3 抛物线
1.掌握抛物线的定义及其焦点、准线的概念.
2.会求简单的抛物线方程.
学习目标
通过前面的学习可以发现,如果动点M到定点F的距离与M到定直线l(不过点F)的距离之比为k,当0
导语
随堂演练
课时对点练
一、抛物线的定义
二、抛物线定义的应用
三、抛物线的实际应用问题
内容索引
一、抛物线的定义
问题1 利用信息技术作图,如图所示,F是定点,l是不经过点F的定直线,H是直线l上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,点M随之运动,你能发现点M满足的几何条件吗?它的轨迹是什么形状?
提示 点M随着点H运动的过程中,始终有|MF|=|MH|,即点M与定点F的距离等于它到定直线l的距离,点M的轨迹形状与二次函数的图象相似.
1.定义:平面内与一个定点F和一条定直线l(不经过点F)的 的点的轨迹叫做抛物线.
2.焦点:定点 .
3.准线:定直线 .
注意点:
(1)“一动三定”:一动点M;一定点F(即焦点);一定直线l(即准线);一定值1(即动点M到定点F的距离与到定直线l的距离之比为1).
(2)若点F在直线l上,点的轨迹是过点F且垂直于直线l的直线.
距离相等
F
知识梳理
l
问题2 比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,可能使所求抛物线的方程形式简单?
提示 我们取经过点F且垂直于直线l的直线为x轴,垂足为K,并使原点与线段KF的中点重合,建立平面直角坐标系Oxy.
设M(x,y)是抛物线上任意一点,点M到准线l的距离为d.由抛物线的定义,抛物线是点的集合P={M||MF|=d}.
将上式两边平方并化简,得y2=2px(p>0).
图形 标准方程 焦点坐标 准线方程
_____________ _________
__________
_______________ ________
__________
y2=2px(p>0)
知识梳理
y2=-2px(p>0)
_____________ _________
___________
_______________ ________
______
x2=2py(p>0)
x2=-2py(p>0)
注意点:
(1)p的几何意义是焦点到准线的距离.
(2)标准方程的结构特征:顶点在坐标原点、焦点在坐标轴上.
(3)抛物线的开口方向:抛物线的开口方向取决于一次项变量(x或y)的取值范围.
例1 分别求符合下列条件的抛物线的标准方程.
(1)经过点(-3,-1);
解 因为点(-3,-1)在第三象限,
所以设所求抛物线的标准方程为y2=-2px(p>0)或x2=-2py(p>0).
若抛物线的标准方程为y2=-2px(p>0),
若抛物线的标准方程为x2=-2py(p>0),
(2)焦点为直线3x-4y-12=0与坐标轴的交点.
解 对于直线方程3x-4y-12=0,
令x=0,得y=-3;令y=0,得x=4,
所以抛物线的焦点为(0,-3)或(4,0).
此时抛物线的标准方程为x2=-12y;
此时抛物线的标准方程为y2=16x.
故所求抛物线的标准方程为x2=-12y或y2=16x.
反思感悟 用待定系数法求抛物线标准方程的步骤
注意:当抛物线的类型没有确定时,可设方程为y2=mx(m≠0)或x2=ny(n≠0),这样可以减少讨论情况的个数.
跟踪训练1 (1)若抛物线y2=2px(p>0)的焦点坐标为(1,0),则p=_____,准线方程为________.
2
x=-1
解析 因为抛物线的焦点坐标为(1,0),
(2)焦点在y轴上,焦点到准线的距离为5的抛物线的标准方程为________
____________.
解析 设方程为x2=2my(m≠0),
由焦点到准线的距离为5,
知|m|=5,m=±5,
所以满足条件的抛物线有两条,它们的标准方程分别为x2=10y和x2=
-10y.
x2=10y
和x2=-10y
二、抛物线定义的应用
例2 (1)已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=
则x0等于
A.1 B.2 C.4 D.8
√
∴x0=1.
(2)已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.
解 由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.
延伸探究
1.若将本例(2)中的点(0,2)改为点A(3,2),求|PA|+|PF|的最小值.
解 将x=3代入y2=2x,
所以点A在抛物线内部.
则|PA|+|PF|=|PA|+d.
解 如图,作PQ垂直于准线l于点Q,
|PA1|+|PQ|=|PA1|+|PF|≥|A1F|min.
即所求最小值为1.
反思感悟 抛物线定义的应用
实现距离转化.根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距与点线距的相互转化,从而简化某些问题.
跟踪训练2 (1)已知抛物线y2=2px(p>0)的焦点F1,若点A(2,-4)在抛物线上,则点A到焦点的距离为_____.
解析 把点(2,-4)代入抛物线y2=2px,得16=4p,
即p=4,从而抛物线的焦点为(2,0).
故点A到焦点的距离为4.
4
(2)设点A的坐标为(1, ),点P在抛物线y2=8x上移动,P到直线x=-1的距离为d,则d+|PA|的最小值为
A.1 B.2 C.3 D.4
√
解析 由题意知抛物线y2=8x的焦点为F(2,0),点P到准线x=-2的距离为d+1,于是|PF|=d+1,
所以d+|PA|=|PF|-1+|PA|的最小值为|AF|-1=4-1=3.
三、抛物线的实际应用问题
例3 河上有一抛物线形拱桥,当水面距拱桥顶5 m时,水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的部分高0.75 m,问:水面上涨到与抛物线拱桥拱顶相距多少米时,小船开始不能通航?
解 如图,以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,
建立平面直角坐标系.设抛物线方程为x2=-2py(p>0),
由题意可知,点B(4,-5)在抛物线上,
当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA′,
又知船面露出水面上的部分高为0.75 m,所以h=|yA|+0.75=2(m).
所以水面上涨到与抛物线形拱桥拱顶相距2 m时,小船开始不能通航.
反思感悟 涉及拱桥、隧道的问题,通常需建立适当的平面直角坐标系,利用抛物线的标准方程进行求解.
跟踪训练3 某桥的桥形可近似地看成抛物线,该桥的高度为h,跨径为a,则桥形对应的抛物线的焦点到准线的距离为
√
解析 如图所示,以桥顶为坐标原点,桥形的对称轴为y轴建立平面直角坐标系Oxy.设抛物线为x2=-2py(p>0),
1.知识清单:
(1)抛物线的定义.
(2)抛物线的标准方程的四种形式.
(3)抛物线定义的应用.
2.方法归纳:待定系数法、定义法、转化化归.
3.常见误区:混淆抛物线的焦点位置和方程形式.
课堂小结
随堂演练
由此可知准线方程为y=2.
√
1
2
3
4
2.已知抛物线y=2px2过点(1,4),则该抛物线的焦点坐标为
√
1
2
3
4
解析 由抛物线y=2px2过点(1,4),可得p=2,
∴右顶点的坐标为(4,0).
设抛物线的标准方程为y2=2px(p>0),
1
2
3
4
y2=16x
∴抛物线的标准方程为y2=16x.
4.若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,则点M的坐标为____________________.
(-9,6)或(-9,-6)
1
2
3
4
解析 由抛物线方程y2=-2px(p>0),
设点M到准线的距离为d,
得p=2,故抛物线方程为y2=-4x.
由点M(-9,y)在抛物线上,得y=±6,
故点M的坐标为(-9,6)或(-9,-6).
课时对点练
1.准线与x轴垂直,且经过点(1,- )的抛物线的标准方程是
A.y2=-2x B.y2=2x
C.x2=2y D.x2=-2y
√
解析 由题意可设抛物线的标准方程为y2=2px(p> 0),
则(- )2=2p,
解得p=1,因此抛物线的标准方程为y2=2x.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)经过点P(4,-2)的抛物线的标准方程可以为
A.y2=x B.x2=8y
C.x2=-8y D.y2=-8x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 若抛物线的焦点在x轴上,
设抛物线的方程为y2=2px(p>0),
又因为抛物线经过点P(4,-2),
所以(-2)2=2p×4,
解得p= ,
所以抛物线的方程为y2=x.
若抛物线的焦点在y轴上,设抛物线的方程为x2=-2py(p>0),
又因为抛物线经过点P(4,-2),
所以42=-2p×(-2),解得p=4,所以抛物线的方程为x2=-8y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.过点A(3,0)且与y轴相切的圆的圆心轨迹为
A.圆 B.椭圆
C.直线 D.抛物线
√
解析 由题意可知,
动圆的圆心到点A的距离与到y轴的距离相等,满足抛物线的定义,
故应选D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知抛物线的顶点在原点,对称轴为x轴,焦点在双曲线 上,则抛物线的方程为
A.y2=8x B.y2=4x
C.y2=2x D.y2=±8x
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即为(-2,0)或(2,0),
所以抛物线的方程为y2=8x或y2=-8x.
5.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是
√
解析 易知直线l2:x=-1恰为抛物线y2=4x的准线,
如图所示,动点P到l2:x=-1的距离可转化为PF的长度,
其中F(1,0)为抛物线y2=4x的焦点.由图可知,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.为响应国家“节能减排,开发清洁能源”的号召,小华制作了一个太阳灶,如图所示.集光板由抛物面(抛物线绕对称轴旋转得到)形的反光镜构成,已知镜口圆的直径为2 m,镜深0.25 m,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.0.5 m B.1 m C.1.5 m D.2 m
√
解析 若使吸收太阳光的效果最好,容器灶圈应在抛物面对应轴截面的抛物线的焦点处,
如图,画出抛物面的轴截面,并建立坐标系,
设抛物线方程为x2=2py(p>0),集光板端点A(1,0.25) ,
代入抛物线方程可得2×0.25p=1,p=2,
所以抛物线方程为x2=4y,故焦点坐标是F(0,1).
所以容器灶圈应距离集光板顶点1 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵抛物线y2=8x的准线方程为x=-2,
该双曲线的一个焦点在抛物线y2=8x的准线上,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴a2+b2=4, ②
由①②,得a2=3,b2=1,
8.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上的一点,PA⊥l,A为垂足,如果直线AF的斜率为- 那么|PF|=___.
8
解析 如图,∠AFE=60°,
因为F(2,0),
所以E(-2,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故|PF|=|PA|=6+2=8.
9.根据下列条件分别求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x2-9y2=144的左顶点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴p=6,∴抛物线的方程为y2=-12x.
(2)抛物线的焦点F在x轴上,直线y=-3与抛物线交于点A,|AF|=5.
解 设所求焦点在x轴上的抛物线的方程为y2=2px(p≠0),A(m,-3),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又(-3)2=2pm,
∴p=±1或p=±9,
故所求抛物线方程为y2=±2x或y2=±18x.
10.已知抛物线C:x2=2py(p>0)上两点A,B且AB⊥y轴,OA⊥OB,△AOB的面积为16,求抛物线C的方程.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 不妨设点A在第一象限且A(m,n),
则B(-m,n),可得m2=2pn,
AB⊥y轴,且OA⊥OB,
即△AOB为等腰直角三角形,
则OA的斜率为1,即m=n,
解得m=n=4,p=2,所以抛物线C的方程为x2=4y.
√
解析 由题意知,A为抛物线的焦点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
则|PA|+|PB|=d+|PB|,d+|PB|的最小值为B到准线的距离,
当PB垂直于准线时取最小值.
√
解析 过点Q作QQ′⊥l于点Q′,如图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴|PQ|∶|PF|=3∶4,
又焦点F到准线l的距离为4,
∴|QF|=|QQ′|=3.
6
解析 设A(x1,y1),B(x2,y2),C(x3,y3),又F(1,0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即x1+x2+x3=3,
14.对标准形式的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).
其中满足抛物线方程为y2=10x的是________.(要求填写适合条件的序号)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②④
解析 抛物线y2=10x的焦点在x轴上,②满足,①不满足;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若由原点向该直线作垂线,垂足为(2,1)时,
则k=-2,此时存在,
所以④满足.
15.已知P为抛物线x2=12y上一个动点,Q为圆(x-4)2+y2=1上一个动点,则点P到点Q的距离与点P到x轴距离之和的最小值是
A.4 B.3
C.2 D.1
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由抛物线的方程可知焦点F(0,3),则准线方程为y=-3,
如图,过点P作x轴的垂线,垂足为点A,延长PA交准线于点B,设圆(x-4)2+y2=1的圆心为点C.
根据抛物线的定义可得|PA|=|PB|-|AB|=|PF|-|AB|,
∴|PA|+|PQ|=|PF|+|PQ|-|AB|=|PF|+|PQ|-3,
∴当|PA|+|PQ|最小时,则|PF|+|PQ|最小,即F,P,Q(Q位于C,P之间)三点共线时,|PA|+|PQ|最小,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴(|PA|+|PQ|)min=(|PF|+|PQ|)min-3=4-3=1.
16.设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.
(1)若点P到直线x=-1的距离为d,A(-1,1),求|PA|+d的最小值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 依题意,抛物线的焦点为F(1,0),准线方程为x=-1.
由抛物线的定义,知|PF|=d,
于是问题转化为求|PA|+|PF|的最小值.
如图,连接AF,交抛物线于点P,
(2)若B(3,2),求|PB|+|PF|的最小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
过点B作BQ垂直于准线于点Q,交抛物线于点P1(如图).
由抛物线的定义,知|P1Q|=|P1F|,
则|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=3+1=4.
即|PB|+|PF|的最小值为4.
