第一章 §1.1 1.1.2空间向量的数量积运算 课件(共59张PPT)
文档属性
| 名称 | 第一章 §1.1 1.1.2空间向量的数量积运算 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 22:00:24 | ||
图片预览







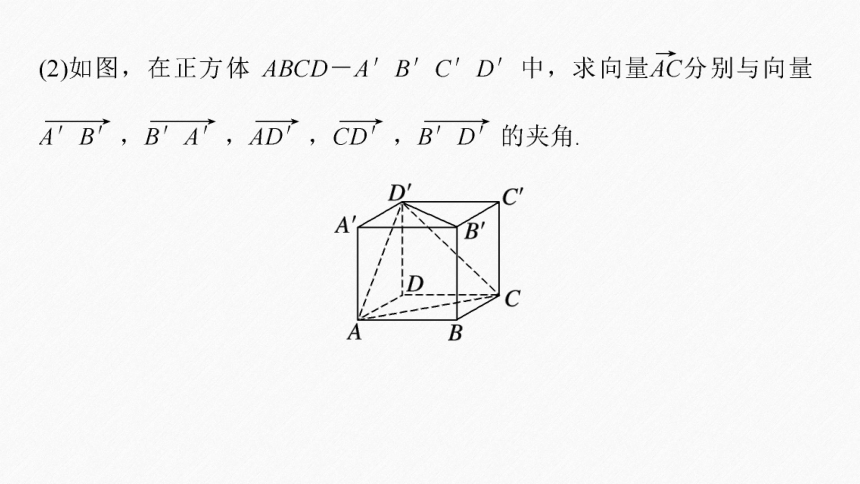
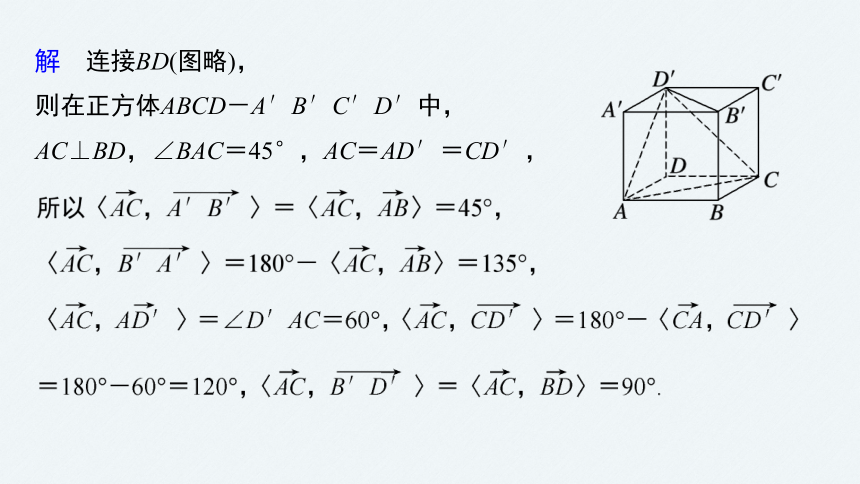



文档简介
(共59张PPT)
1.1.2 空间向量的数量积运算
第一章 §1.1 空间向量及其运算
1.了解空间向量的夹角.
2.掌握空间向量的数量积的定义、性质、运算律及计算方法.
3.了解空间向量投影的概念以及投影向量的意义.
4.掌握两个向量的数量积在判断垂直中的应用,掌握利用向量数量积求
空间两点间的距离.
学习目标
在平面向量中已经学过两个平面向量的数量积运算,由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
导语
随堂演练
课时对点练
一、空间向量的夹角
二、空间向量的数量积运算
三、利用空间向量数量积的性质求模长
内容索引
一、空间向量的夹角
定义 已知两个非零向量a,b,在空间任取一点O,作
则 叫做向量a,b的夹角,记作〈a,b〉
范围 ________________
向量垂直 如果〈a,b〉= ,那么向量a,b互相垂直,记作a b
知识梳理
∠AOB
⊥
0≤〈a,b〉≤π
例1 (1)对于空间任意两个非零向量a,b,“a∥b”是“〈a,b〉=0”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
√
解析 显然〈a,b〉=0 a∥b,
但a∥b包括向量a,b同向共线和反向共线两种情况,
即当a∥b时,〈a,b〉=0或π,因此a∥b 〈a,b〉=0.
故“a∥b”是“〈a,b〉=0”的必要不充分条件.
解 连接BD(图略),
则在正方体ABCD-A′B′C′D′中,
AC⊥BD,∠BAC=45°,AC=AD′=CD′,
反思感悟 (1)只有两个非零空间向量才有夹角,当两个非零空间向量共线同向时,夹角为0,共线反向时,夹角为π.
(2)对空间任意两个非零向量a,b有:①〈a,b〉=〈b,a〉;②〈-a,b〉=〈a,-b〉;③〈-a,-b〉=〈a,b〉.
A.30° B.60° C.150° D.120°
√
二、空间向量的数量积运算
1.(1)空间向量的数量积
已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b,即a·b= .零向量与任意向量的数量积为0,即0·a= .
(2)运算律
|a||b|·cos〈a,b〉
0
知识梳理
数乘向量与数量积的结合律 (λa)·b= ,λ∈R
交换律 a·b=____
分配律 a·(b+c)=________
λ(a·b)
b·a
a·b+a·c
2.向量的投影
(1)如图①,在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图②).
(2)如图③,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
注意点:
(1)向量a,b的数量积记为a·b,而不能表示为a×b或者ab.
(2)向量的数量积的结果为实数,而不是向量,它可以是正数、负数或零,其符号由夹角θ的范围决定.
①当θ为锐角时,a·b>0;但当a·b>0时,θ不一定为锐角,因为θ也可能为0.
②当θ为钝角时,a·b<0;但当a·b<0时,θ不一定为钝角,因为θ也可能为π.
(3)空间向量的数量积运算不满足消去律和结合律.
例2 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
反思感悟 由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.
跟踪训练2 已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为______.
解析 ∵a+b+c=0,
∴(a+b+c)2=0,
∴a2+b2+c2+2(a·b+b·c+c·a)=0,
-13
三、利用空间向量数量积的性质求模长
问题 类比平面向量数量积的性质,给出空间向量数量积的性质.
提示 (1)若a,b为非零向量,则a⊥b a·b=0;
(4)|a·b|≤|a||b|(当且仅当a,b共线时等号成立).
例3 如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
解 ∵CA⊥AB,BD⊥AB,
反思感悟 用数量积求两点间距离的步骤
(1)将两点间的连线用向量表示;
(2)用其他向量表示此向量;
(3)用公式a·a=|a|2,求|a|.
跟踪训练3 已知在平行六面体ABCD-A1B1C1D1中,AA1=AB=AD=1,且这三条棱彼此之间的夹角都是60°,则AC1的长为
√
则|a|=|b|=|c|=1,
且〈a,b〉=〈b,c〉=〈c,a〉=60°,
1.知识清单:
(1)空间向量的夹角、投影.
(2)空间向量数量积、性质及运算律.
2.方法归纳:化归转化.
3.常见误区:
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0时,由a·b=0可得a⊥b或b=0.
课堂小结
随堂演练
1.(多选)如图所示,在正方体ABCD-A1B1C1D1中,下列各组向量的夹角为45°的是
√
1
2
3
4
√
√
1
2
3
4
3.若a,b为空间夹角是60°的两个单位向量,则|a-b|=____.
1
2
3
4
1
解析 |a-b|2=(a-b)2
=a2+b2-2a·b=1.
∴|a-b|=1.
60° 1
1
2
3
4
解析 方法一 连接A1D(图略),
1
2
3
4
即△PA1D为等边三角形,从而∠PA1D=60°,
方法二 根据向量的线性运算可得
1
2
3
4
课时对点练
1.在正四面体A-BCD中,点E,F分别是AC,AD的中点, 的夹角为
A.30° B.60° C.120° D.150°
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a-b)·a等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b= 则两直线的夹角为
A.30° B.60° C.120° D.150°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则两个方向向量对应的直线的夹角为180°-120°=60°.
4.(多选)如图所示,已知空间四边形每条边和对角线长都为a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
5.平行六面体(底面为平行四边形的四棱柱)ABCD-A1B1C1D1的所有棱长都为1,且∠A1AD=∠A1AB=60°,∠DAB=45°,则BD1等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)在正方体ABCD-A1B1C1D1中,下列命题是真命题的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知|a|=13,|b|=19,|a+b|=24,则|a-b|=_____.
22
解析 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,
∴2a·b=46,|a-b|2=a2-2a·b+b2=530-46=484,
故|a-b|=22.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
60°
解析 由条件知(a+3b)·(7a-5b)=7|a|2-15|b|2+16a·b=0,
(a-4b)·(7a-2b)=7|a|2+8|b|2-30a·b=0,两式相减得46a·b=23|b|2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以〈a,b〉=60°.
9.已知在长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AB1的中心,F为A1D1的中点,试计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则|a|=|c|=2,|b|=4,a·b=b·c=c·a=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,在空间四面体OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.如图,在大小为45°的二面角A-EF-D中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.如图,已知在平行四边形ABCD中,AD=4,CD=3,∠D=60°,PA⊥平面ABCD,且PA=6,则PC=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7
解析 ∵OA,OB,OC两两垂直,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知正方体ABCD-A1B1C1D1的棱长为1,若动点P在线段BD1上运动,
的取值范围是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[0,1]
A.8 B.4 C.2 D.1
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵AB⊥平面BP2P8P6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D两点间的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 在平行四边形ABCD中,
∵∠ACD=90°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在空间四边形ABCD中,
∵AB与CD成60°角,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
此时B,D两点间的距离为2,
1.1.2 空间向量的数量积运算
第一章 §1.1 空间向量及其运算
1.了解空间向量的夹角.
2.掌握空间向量的数量积的定义、性质、运算律及计算方法.
3.了解空间向量投影的概念以及投影向量的意义.
4.掌握两个向量的数量积在判断垂直中的应用,掌握利用向量数量积求
空间两点间的距离.
学习目标
在平面向量中已经学过两个平面向量的数量积运算,由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
导语
随堂演练
课时对点练
一、空间向量的夹角
二、空间向量的数量积运算
三、利用空间向量数量积的性质求模长
内容索引
一、空间向量的夹角
定义 已知两个非零向量a,b,在空间任取一点O,作
则 叫做向量a,b的夹角,记作〈a,b〉
范围 ________________
向量垂直 如果〈a,b〉= ,那么向量a,b互相垂直,记作a b
知识梳理
∠AOB
⊥
0≤〈a,b〉≤π
例1 (1)对于空间任意两个非零向量a,b,“a∥b”是“〈a,b〉=0”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
√
解析 显然〈a,b〉=0 a∥b,
但a∥b包括向量a,b同向共线和反向共线两种情况,
即当a∥b时,〈a,b〉=0或π,因此a∥b 〈a,b〉=0.
故“a∥b”是“〈a,b〉=0”的必要不充分条件.
解 连接BD(图略),
则在正方体ABCD-A′B′C′D′中,
AC⊥BD,∠BAC=45°,AC=AD′=CD′,
反思感悟 (1)只有两个非零空间向量才有夹角,当两个非零空间向量共线同向时,夹角为0,共线反向时,夹角为π.
(2)对空间任意两个非零向量a,b有:①〈a,b〉=〈b,a〉;②〈-a,b〉=〈a,-b〉;③〈-a,-b〉=〈a,b〉.
A.30° B.60° C.150° D.120°
√
二、空间向量的数量积运算
1.(1)空间向量的数量积
已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b,即a·b= .零向量与任意向量的数量积为0,即0·a= .
(2)运算律
|a||b|·cos〈a,b〉
0
知识梳理
数乘向量与数量积的结合律 (λa)·b= ,λ∈R
交换律 a·b=____
分配律 a·(b+c)=________
λ(a·b)
b·a
a·b+a·c
2.向量的投影
(1)如图①,在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉 向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图②).
(2)如图③,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向量a所在直线与平面β所成的角.
注意点:
(1)向量a,b的数量积记为a·b,而不能表示为a×b或者ab.
(2)向量的数量积的结果为实数,而不是向量,它可以是正数、负数或零,其符号由夹角θ的范围决定.
①当θ为锐角时,a·b>0;但当a·b>0时,θ不一定为锐角,因为θ也可能为0.
②当θ为钝角时,a·b<0;但当a·b<0时,θ不一定为钝角,因为θ也可能为π.
(3)空间向量的数量积运算不满足消去律和结合律.
例2 如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
反思感悟 由向量数量积的定义知,要求a与b的数量积,需已知|a|,|b|和〈a,b〉,a与b的夹角与方向有关,一定要根据方向正确判定夹角的大小,才能使a·b计算准确.
跟踪训练2 已知空间向量a,b,c满足a+b+c=0,|a|=3,|b|=1,|c|=4,则a·b+b·c+c·a的值为______.
解析 ∵a+b+c=0,
∴(a+b+c)2=0,
∴a2+b2+c2+2(a·b+b·c+c·a)=0,
-13
三、利用空间向量数量积的性质求模长
问题 类比平面向量数量积的性质,给出空间向量数量积的性质.
提示 (1)若a,b为非零向量,则a⊥b a·b=0;
(4)|a·b|≤|a||b|(当且仅当a,b共线时等号成立).
例3 如图,已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这两个面内且垂直于AB的线段.又知AB=4,AC=6,BD=8,求CD的长.
解 ∵CA⊥AB,BD⊥AB,
反思感悟 用数量积求两点间距离的步骤
(1)将两点间的连线用向量表示;
(2)用其他向量表示此向量;
(3)用公式a·a=|a|2,求|a|.
跟踪训练3 已知在平行六面体ABCD-A1B1C1D1中,AA1=AB=AD=1,且这三条棱彼此之间的夹角都是60°,则AC1的长为
√
则|a|=|b|=|c|=1,
且〈a,b〉=〈b,c〉=〈c,a〉=60°,
1.知识清单:
(1)空间向量的夹角、投影.
(2)空间向量数量积、性质及运算律.
2.方法归纳:化归转化.
3.常见误区:
(1)数量积的符号由夹角的余弦值决定.
(2)当a≠0时,由a·b=0可得a⊥b或b=0.
课堂小结
随堂演练
1.(多选)如图所示,在正方体ABCD-A1B1C1D1中,下列各组向量的夹角为45°的是
√
1
2
3
4
√
√
1
2
3
4
3.若a,b为空间夹角是60°的两个单位向量,则|a-b|=____.
1
2
3
4
1
解析 |a-b|2=(a-b)2
=a2+b2-2a·b=1.
∴|a-b|=1.
60° 1
1
2
3
4
解析 方法一 连接A1D(图略),
1
2
3
4
即△PA1D为等边三角形,从而∠PA1D=60°,
方法二 根据向量的线性运算可得
1
2
3
4
课时对点练
1.在正四面体A-BCD中,点E,F分别是AC,AD的中点, 的夹角为
A.30° B.60° C.120° D.150°
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.已知向量a和b的夹角为120°,且|a|=2,|b|=5,则(2a-b)·a等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b= 则两直线的夹角为
A.30° B.60° C.120° D.150°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则两个方向向量对应的直线的夹角为180°-120°=60°.
4.(多选)如图所示,已知空间四边形每条边和对角线长都为a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
5.平行六面体(底面为平行四边形的四棱柱)ABCD-A1B1C1D1的所有棱长都为1,且∠A1AD=∠A1AB=60°,∠DAB=45°,则BD1等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)在正方体ABCD-A1B1C1D1中,下列命题是真命题的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知|a|=13,|b|=19,|a+b|=24,则|a-b|=_____.
22
解析 |a+b|2=a2+2a·b+b2=132+2a·b+192=242,
∴2a·b=46,|a-b|2=a2-2a·b+b2=530-46=484,
故|a-b|=22.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知a+3b与7a-5b垂直,且a-4b与7a-2b垂直,则〈a,b〉=_____.
60°
解析 由条件知(a+3b)·(7a-5b)=7|a|2-15|b|2+16a·b=0,
(a-4b)·(7a-2b)=7|a|2+8|b|2-30a·b=0,两式相减得46a·b=23|b|2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以〈a,b〉=60°.
9.已知在长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AB1的中心,F为A1D1的中点,试计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则|a|=|c|=2,|b|=4,a·b=b·c=c·a=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,在空间四面体OABC中,OA,OB,OC两两成60°角,且OA=OB=OC=2,E为OA的中点,F为BC的中点,试求E,F间的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.如图,在大小为45°的二面角A-EF-D中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.如图,已知在平行四边形ABCD中,AD=4,CD=3,∠D=60°,PA⊥平面ABCD,且PA=6,则PC=_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7
解析 ∵OA,OB,OC两两垂直,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知正方体ABCD-A1B1C1D1的棱长为1,若动点P在线段BD1上运动,
的取值范围是______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[0,1]
A.8 B.4 C.2 D.1
√
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵AB⊥平面BP2P8P6,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D两点间的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 在平行四边形ABCD中,
∵∠ACD=90°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
在空间四边形ABCD中,
∵AB与CD成60°角,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
此时B,D两点间的距离为2,
