第一章 §1.3 1.3.1空间直角坐标系 课件(共52张PPT)
文档属性
| 名称 | 第一章 §1.3 1.3.1空间直角坐标系 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 22:03:26 | ||
图片预览











文档简介
(共52张PPT)
1.3.1 空间直角坐标系
第一章 §1.3 空间向量及其运算的坐标表示
1.了解空间直角坐标系.
2.能在空间直角坐标系中写出所给定点、向量的坐标.
学习目标
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法….”
导语
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
随堂演练
课时对点练
一、空间直角坐标系
二、求空间点的坐标
三、空间点的对称问题
内容索引
四、空间向量的坐标
一、空间直角坐标系
1.空间直角坐标系:在空间选定一点O和一个单位正交基底{i,j,k},以O为原点,分别以i,j,k的方向为正方向,以它们的长为单位长度建立三条数轴: ,它们都叫做坐标轴,这时我们就建立了一个
.
2.相关概念: 叫做原点,i,j,k都叫做坐标向量,通过 的平面叫做坐标平面,分别称为 平面、 平面、 平面,它们把空间分成八个部分.
x轴、y轴、z轴
空间直角坐标系Oxyz
知识梳理
O
每两条坐标轴
Oxy
Oyz
Ozx
注意点:
(1)基向量:|i|=|j|=|k|=1,i·j=i·k=j·k=0.
(2)画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
(3)建立的坐标系均为右手直角坐标系.
二、求空间点的坐标
在空间直角坐标系Oxyz中,i,j,k为坐标向量,对空间任意一点A,对应一个向量 ,且点A的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使 = .在单位正交
xi+yj+zk
知识梳理
基底{i,j,k}下与向量 对应的有序实数组 ,叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的 ,y叫做点A的 ,z叫做点A的 .
(x,y,z)
横坐标
纵坐标
竖坐标
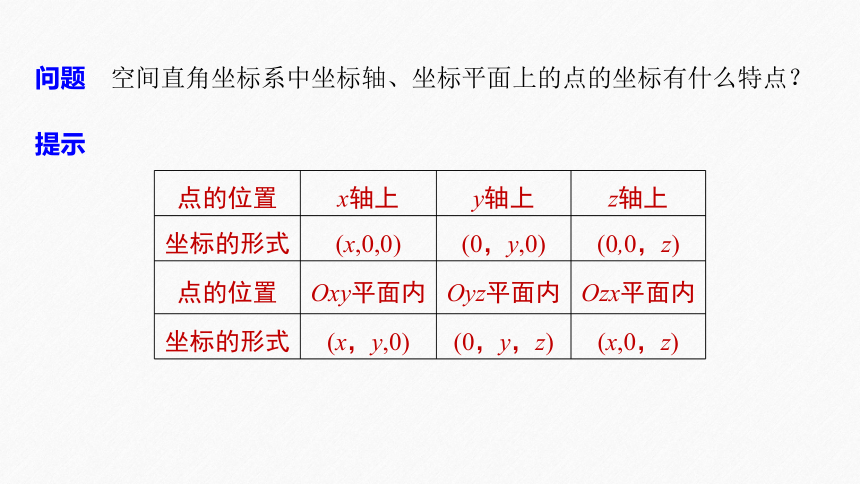
问题 空间直角坐标系中坐标轴、坐标平面上的点的坐标有什么特点?
提示
点的位置 x轴上 y轴上 z轴上
坐标的形式 (x,0,0) (0,y,0) (0,0,z)
点的位置 Oxy平面内 Oyz平面内 Ozx平面内
坐标的形式 (x,y,0) (0,y,z) (x,0,z)
例1 (1)画一个正方体ABCD-A1B1C1D1,若以A为坐标原点,以棱AB,AD,AA1所在的直线分别为x轴、y轴、z轴,取正方体的棱长为单位长度,建立空间直角坐标系,则
①顶点A,D1的坐标分别为________________;
②棱C1C中点的坐标为___________;
③正方形AA1B1B对角线的交点的坐标为___________.
(0,0,0),(0,1,1)
(2)已知正四棱锥P-ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.
解 ∵正四棱锥P-ABCD的底面边长为4,侧棱长为10,
以正四棱锥的底面中心为原点,平行于BC,AB所在的直线分别为x轴、y轴,垂直于平面ABCD的直线为z轴,
建立如图所示的空间直角坐标系,
则正四棱锥各顶点的坐标分别为A(2,-2,0),B(2,2,0),C(-2,2,0),D(-2,-2,0),
答案不唯一.
反思感悟 (1)建立空间直角坐标系的原则
①让尽可能多的点落在坐标轴上或坐标平面内.
②充分利用几何图形的对称性.
(2)求某点M的坐标的方法
作MM′垂直于平面Oxy,垂足为M′,求M′的横坐标x,纵坐标y,即点M的横坐标x,纵坐标y,再求M点在z轴上射影的竖坐标z,即为M点的竖坐标z,于是得到M点的坐标(x,y,z).
跟踪训练1 设正四棱锥S-P1P2P3P4的所有棱长均为2,建立适当的空间直角坐标系,求各个顶点的坐标.
解 如图所示,建立空间直角坐标系,其中O为底面正方形的中心,P1P2⊥Oy轴,P1P4⊥Ox轴,SO在Oz轴上.
∵P1P2=2,且P1,P2,P3,P4均在Oxy平面上,
∴P1(1,1,0),P2(-1,1,0).
在Oxy平面内,P3与P1关于原点O对称,P4与P2关于原点O对称,
∴P3(-1,-1,0),P4(1,-1,0).
(答案不唯一,也可选择其他的点建系)
三、空间点的对称问题
例2 在空间直角坐标系中,已知点P(-2,1,4).
(1)求点P关于x轴对称的点的坐标;
解 由于点P关于x轴对称后,它在x轴的分量不变,
在y轴、z轴的分量变为原来的相反数,
所以对称点坐标为P1(-2,-1,-4).
(2)求点P关于Oxy平面对称的点的坐标;
解 由点P关于Oxy平面对称后,它在x轴、y轴的分量不变,
在z轴的分量变为原来的相反数,
所以对称点坐标为P2(-2,1,-4).
(3)求点P关于点M(2,-1,-4)对称的点的坐标.
解 设对称点为P3(x,y,z),则点M为线段PP3的中点,
由中点坐标公式,可得x=2×2-(-2)=6,
y=2×(-1)-1=-3,z=2×(-4)-4=-12,
所以P3的坐标为(6,-3,-12).
反思感悟 空间点对称问题的解题策略
(1)空间点的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.
(2)对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论.
跟踪训练2 已知点P(2,3,-1)关于坐标平面Oxy的对称点为P1,点P1关于坐标平面Oyz的对称点为P2,点P2关于z轴的对称点为P3,则点P3的坐标为____________.
解析 点P(2,3,-1)关于坐标平面Oxy的对称点P1的坐标为(2,3,1),
点P1关于坐标平面Oyz的对称点P2的坐标为(-2,3,1),
点P2关于z轴的对称点P3的坐标是(2,-3,1).
(2,-3,1)
四、空间向量的坐标
向量的坐标:在空间直角坐标系Oxyz中,给定向量a,作 =a,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=xi+yj+zk.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,可简记作a= .
(x,y,z)
知识梳理
=0i+4j+4k
=(0,4,4),
=-4i+4j+4k=(-4,4,4).
反思感悟 向量坐标的求法
(1)点A的坐标和向量 的坐标形式完全相同;
(2)起点不是原点的向量的坐标可以通过向量的运算求得.
跟踪训练3 如图所示,以长方体ABCD-A1B1C1D的顶点D为坐标原点,过D的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为(4,3,2),则C1的坐标是
A.(0,3,2) B.(0,4,2)
C.(4,0,2) D.(2,3,4)
√
∴B1的坐标为(4,3,2),
∴BC=4,DC=3,CC1=2,
∴C1的坐标为(0,3,2).
1.知识清单:
(1)空间直角坐标系的概念.
(2)空间点的坐标.
(3)空间向量的坐标.
2.方法归纳:数形结合、类比联想.
3.常见误区:混淆空间点的坐标和向量坐标的概念,只有起点在原点的向量的坐标才和终点的坐标相同.
课堂小结
随堂演练
1.在空间直角坐标系中,点P(1,3,-5)关于平面Oxy对称的点的坐标是
A.(-1,3,-5) B.(1,3,5)
C.(1,-3,5) D.(-1,-3,5)
√
1
2
3
4
2.在空间直角坐标系中,点P(-1,-2,-3)到平面Oyz的距离是
A.1 B.2
C.3 D.
√
1
2
3
4
解析 点到平面Oyz的距离就是点的横坐标的绝对值.
3.点P(1,1,1)关于Oxy平面的对称点P1的坐标为___________,点P关于z轴的对称点P2的坐标为______________.
1
2
3
4
(1,1,-1)
(-1,-1,1)
解析 点P(1,1,1)关于Oxy平面的对称点P1的坐标为(1,1,-1),
点P关于z轴的对称点P2的坐标为(-1,-1,1).
4.在长方体ABCD-A1B1C1D1中,若D(0,0,0),A(4,0,0),B(4,2,0),A1(4,0,3),则向量 的坐标为_________.
(-4,2,3)
1
2
3
4
课时对点练
1.(多选)下列命题中正确的是
A.在空间直角坐标系中,在x轴上的点的坐标一定是(0,b,c)
B.在空间直角坐标系中,在Oyz平面上的点的坐标一定是(0,b,c)
C.在空间直角坐标系中,在z轴上的点的坐标可记作(0,0,c)
D.在空间直角坐标系中,在Ozx平面上的点的坐标是(a,0,c)
√
解析 空间直角坐标系中,在x轴上的点的坐标是(a,0,0).故A错误,B,C,D正确.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
2.在空间直角坐标系Oxyz中,点(1,-2,4)关于y轴对称的点为
A.(-1,-2,-4) B.(-1,-2,4)
C.(1,2,-4) D.(1,2,4)
√
解析 关于y 轴对称,则y值不变,x和z的值变为原来的相反数,
故所求的点的坐标为(-1,-2,-4).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.如图,在长方体OABC-O1A1B1C1中,OA=3,OC=5,OO1=4,点P是B1C1的中点,则点P的坐标为
√
解析 由题图知,点P在x轴、y轴、z轴上的射影分别为P1,P2,P3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.在空间直角坐标系中,点(1,2,3)与点(-1,2,3)
A.关于Oxy平面对称 B.关于Ozx平面对称
C.关于Oyz平面对称 D.关于x轴对称
√
解析 空间中的两个点(1,2,3)和(-1,2,3),y,z轴上的两个坐标相同,x轴上的坐标相反,
故此两点关于Oyz平面对称.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由于垂足在平面Oyz上,
所以纵坐标,竖坐标不变,横坐标为0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设{i,j,k}是空间向量的一个单位正交基底,a=2i-4j+5k,b=i+2j-3k,则向量a,b的坐标分别为______________________.
(2,-4,5),(1,2,-3)
解析 由空间向量坐标概念知a=(2,-4,5),b=(1,2,-3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.如图是一个正方体截下的一角P-ABC,其中PA=a,PB=b,PC=c.建立如图所示的空间直角坐标系,则
△ABC的重心G的坐标是__________.
解析 由题意知A(a,0,0),B(0,b,0),C(0,0,c).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.建立空间直角坐标系如图所示,正方体DABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐标.
解 正方体DABC-D′A′B′C′的棱长为a,且E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP,BP,CP,DP,M,N分别是AB,BC的中点,以O为原点,
为单位正交基底建立空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若E,F分别为PA,PB的中点,求点A,B,C,D,E,F的坐标.
解 由题意知,点B的坐标为(1,1,0).
由点A与点B关于x轴对称,得A(1,-1,0),
由点C与点B关于y轴对称,得C(-1,1,0),
由点D与点C关于x轴对称,得D(-1,-1,0).
又P(0,0,2),E为AP的中点,F为PB的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在空间直角坐标系中,点M(1,2,3)到z轴的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.(多选)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴,建立空间直角坐标系,则下列说法正确的是
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 根据题意知,点B1的坐标为(4,5,3),选项A正确;
B的坐标为(4,5,0),C1的坐标为(0,5,3),
故点C1关于点B对称的点为(8,5,-3),选项B错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以四边形ABC1D1为正方形,AC1与BD1垂直且平分,
即点A关于直线BD1对称的点为C1(0,5,3),选项C正确;
点C关于平面ABB1A1对称的点为(8,5,0),选项D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(2,1,-3) B.(-1,2,-3)
C.(1,-8,9) D.(-1,8,-9)
√
14.在三棱锥P-ABC中,∠ABC=90°,PB⊥平面ABC,AB=BC=PB=1,M,N分别是PC,AC的中点,建立如图
所示的坐标系Bxyz,则向量 的坐标为______________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知向量p在基底{a,b,c}下的坐标为(2,1,-1),则p在基底{2a,b,-c}下的坐标为________,在基底{a+b,a-b,c}下的坐
标为____________.
(1,1,1)
解析 由题意知p=2a+b-c,
则向量p在基底{2a,b,-c}下的坐标为(1,1,1).
设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则
p=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,
又∵p=2a+b-c,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图所示,正四面体ABCD的棱长为1,G是△BCD的中心,建立如图所示的空间直角坐标系,则 的坐标为
____________, 的坐标为_________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.3.1 空间直角坐标系
第一章 §1.3 空间向量及其运算的坐标表示
1.了解空间直角坐标系.
2.能在空间直角坐标系中写出所给定点、向量的坐标.
学习目标
我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法….”
导语
吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.
随堂演练
课时对点练
一、空间直角坐标系
二、求空间点的坐标
三、空间点的对称问题
内容索引
四、空间向量的坐标
一、空间直角坐标系
1.空间直角坐标系:在空间选定一点O和一个单位正交基底{i,j,k},以O为原点,分别以i,j,k的方向为正方向,以它们的长为单位长度建立三条数轴: ,它们都叫做坐标轴,这时我们就建立了一个
.
2.相关概念: 叫做原点,i,j,k都叫做坐标向量,通过 的平面叫做坐标平面,分别称为 平面、 平面、 平面,它们把空间分成八个部分.
x轴、y轴、z轴
空间直角坐标系Oxyz
知识梳理
O
每两条坐标轴
Oxy
Oyz
Ozx
注意点:
(1)基向量:|i|=|j|=|k|=1,i·j=i·k=j·k=0.
(2)画空间直角坐标系Oxyz时,一般使∠xOy=135°(或45°),∠yOz=90°.
(3)建立的坐标系均为右手直角坐标系.
二、求空间点的坐标
在空间直角坐标系Oxyz中,i,j,k为坐标向量,对空间任意一点A,对应一个向量 ,且点A的位置由向量 唯一确定,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使 = .在单位正交
xi+yj+zk
知识梳理
基底{i,j,k}下与向量 对应的有序实数组 ,叫做点A在空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的 ,y叫做点A的 ,z叫做点A的 .
(x,y,z)
横坐标
纵坐标
竖坐标
问题 空间直角坐标系中坐标轴、坐标平面上的点的坐标有什么特点?
提示
点的位置 x轴上 y轴上 z轴上
坐标的形式 (x,0,0) (0,y,0) (0,0,z)
点的位置 Oxy平面内 Oyz平面内 Ozx平面内
坐标的形式 (x,y,0) (0,y,z) (x,0,z)
例1 (1)画一个正方体ABCD-A1B1C1D1,若以A为坐标原点,以棱AB,AD,AA1所在的直线分别为x轴、y轴、z轴,取正方体的棱长为单位长度,建立空间直角坐标系,则
①顶点A,D1的坐标分别为________________;
②棱C1C中点的坐标为___________;
③正方形AA1B1B对角线的交点的坐标为___________.
(0,0,0),(0,1,1)
(2)已知正四棱锥P-ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.
解 ∵正四棱锥P-ABCD的底面边长为4,侧棱长为10,
以正四棱锥的底面中心为原点,平行于BC,AB所在的直线分别为x轴、y轴,垂直于平面ABCD的直线为z轴,
建立如图所示的空间直角坐标系,
则正四棱锥各顶点的坐标分别为A(2,-2,0),B(2,2,0),C(-2,2,0),D(-2,-2,0),
答案不唯一.
反思感悟 (1)建立空间直角坐标系的原则
①让尽可能多的点落在坐标轴上或坐标平面内.
②充分利用几何图形的对称性.
(2)求某点M的坐标的方法
作MM′垂直于平面Oxy,垂足为M′,求M′的横坐标x,纵坐标y,即点M的横坐标x,纵坐标y,再求M点在z轴上射影的竖坐标z,即为M点的竖坐标z,于是得到M点的坐标(x,y,z).
跟踪训练1 设正四棱锥S-P1P2P3P4的所有棱长均为2,建立适当的空间直角坐标系,求各个顶点的坐标.
解 如图所示,建立空间直角坐标系,其中O为底面正方形的中心,P1P2⊥Oy轴,P1P4⊥Ox轴,SO在Oz轴上.
∵P1P2=2,且P1,P2,P3,P4均在Oxy平面上,
∴P1(1,1,0),P2(-1,1,0).
在Oxy平面内,P3与P1关于原点O对称,P4与P2关于原点O对称,
∴P3(-1,-1,0),P4(1,-1,0).
(答案不唯一,也可选择其他的点建系)
三、空间点的对称问题
例2 在空间直角坐标系中,已知点P(-2,1,4).
(1)求点P关于x轴对称的点的坐标;
解 由于点P关于x轴对称后,它在x轴的分量不变,
在y轴、z轴的分量变为原来的相反数,
所以对称点坐标为P1(-2,-1,-4).
(2)求点P关于Oxy平面对称的点的坐标;
解 由点P关于Oxy平面对称后,它在x轴、y轴的分量不变,
在z轴的分量变为原来的相反数,
所以对称点坐标为P2(-2,1,-4).
(3)求点P关于点M(2,-1,-4)对称的点的坐标.
解 设对称点为P3(x,y,z),则点M为线段PP3的中点,
由中点坐标公式,可得x=2×2-(-2)=6,
y=2×(-1)-1=-3,z=2×(-4)-4=-12,
所以P3的坐标为(6,-3,-12).
反思感悟 空间点对称问题的解题策略
(1)空间点的对称问题可类比平面直角坐标系中点的对称问题,要掌握对称点的变化规律,才能准确求解.
(2)对称点的问题常常采用“关于谁对称,谁保持不变,其余坐标相反”这个结论.
跟踪训练2 已知点P(2,3,-1)关于坐标平面Oxy的对称点为P1,点P1关于坐标平面Oyz的对称点为P2,点P2关于z轴的对称点为P3,则点P3的坐标为____________.
解析 点P(2,3,-1)关于坐标平面Oxy的对称点P1的坐标为(2,3,1),
点P1关于坐标平面Oyz的对称点P2的坐标为(-2,3,1),
点P2关于z轴的对称点P3的坐标是(2,-3,1).
(2,-3,1)
四、空间向量的坐标
向量的坐标:在空间直角坐标系Oxyz中,给定向量a,作 =a,由空间向量基本定理,存在唯一的有序实数组(x,y,z),使a=xi+yj+zk.有序实数组(x,y,z)叫做a在空间直角坐标系Oxyz中的坐标,可简记作a= .
(x,y,z)
知识梳理
=0i+4j+4k
=(0,4,4),
=-4i+4j+4k=(-4,4,4).
反思感悟 向量坐标的求法
(1)点A的坐标和向量 的坐标形式完全相同;
(2)起点不是原点的向量的坐标可以通过向量的运算求得.
跟踪训练3 如图所示,以长方体ABCD-A1B1C1D的顶点D为坐标原点,过D的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 的坐标为(4,3,2),则C1的坐标是
A.(0,3,2) B.(0,4,2)
C.(4,0,2) D.(2,3,4)
√
∴B1的坐标为(4,3,2),
∴BC=4,DC=3,CC1=2,
∴C1的坐标为(0,3,2).
1.知识清单:
(1)空间直角坐标系的概念.
(2)空间点的坐标.
(3)空间向量的坐标.
2.方法归纳:数形结合、类比联想.
3.常见误区:混淆空间点的坐标和向量坐标的概念,只有起点在原点的向量的坐标才和终点的坐标相同.
课堂小结
随堂演练
1.在空间直角坐标系中,点P(1,3,-5)关于平面Oxy对称的点的坐标是
A.(-1,3,-5) B.(1,3,5)
C.(1,-3,5) D.(-1,-3,5)
√
1
2
3
4
2.在空间直角坐标系中,点P(-1,-2,-3)到平面Oyz的距离是
A.1 B.2
C.3 D.
√
1
2
3
4
解析 点到平面Oyz的距离就是点的横坐标的绝对值.
3.点P(1,1,1)关于Oxy平面的对称点P1的坐标为___________,点P关于z轴的对称点P2的坐标为______________.
1
2
3
4
(1,1,-1)
(-1,-1,1)
解析 点P(1,1,1)关于Oxy平面的对称点P1的坐标为(1,1,-1),
点P关于z轴的对称点P2的坐标为(-1,-1,1).
4.在长方体ABCD-A1B1C1D1中,若D(0,0,0),A(4,0,0),B(4,2,0),A1(4,0,3),则向量 的坐标为_________.
(-4,2,3)
1
2
3
4
课时对点练
1.(多选)下列命题中正确的是
A.在空间直角坐标系中,在x轴上的点的坐标一定是(0,b,c)
B.在空间直角坐标系中,在Oyz平面上的点的坐标一定是(0,b,c)
C.在空间直角坐标系中,在z轴上的点的坐标可记作(0,0,c)
D.在空间直角坐标系中,在Ozx平面上的点的坐标是(a,0,c)
√
解析 空间直角坐标系中,在x轴上的点的坐标是(a,0,0).故A错误,B,C,D正确.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
2.在空间直角坐标系Oxyz中,点(1,-2,4)关于y轴对称的点为
A.(-1,-2,-4) B.(-1,-2,4)
C.(1,2,-4) D.(1,2,4)
√
解析 关于y 轴对称,则y值不变,x和z的值变为原来的相反数,
故所求的点的坐标为(-1,-2,-4).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.如图,在长方体OABC-O1A1B1C1中,OA=3,OC=5,OO1=4,点P是B1C1的中点,则点P的坐标为
√
解析 由题图知,点P在x轴、y轴、z轴上的射影分别为P1,P2,P3,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.在空间直角坐标系中,点(1,2,3)与点(-1,2,3)
A.关于Oxy平面对称 B.关于Ozx平面对称
C.关于Oyz平面对称 D.关于x轴对称
√
解析 空间中的两个点(1,2,3)和(-1,2,3),y,z轴上的两个坐标相同,x轴上的坐标相反,
故此两点关于Oyz平面对称.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由于垂足在平面Oyz上,
所以纵坐标,竖坐标不变,横坐标为0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.设{i,j,k}是空间向量的一个单位正交基底,a=2i-4j+5k,b=i+2j-3k,则向量a,b的坐标分别为______________________.
(2,-4,5),(1,2,-3)
解析 由空间向量坐标概念知a=(2,-4,5),b=(1,2,-3).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.如图是一个正方体截下的一角P-ABC,其中PA=a,PB=b,PC=c.建立如图所示的空间直角坐标系,则
△ABC的重心G的坐标是__________.
解析 由题意知A(a,0,0),B(0,b,0),C(0,0,c).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.建立空间直角坐标系如图所示,正方体DABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐标.
解 正方体DABC-D′A′B′C′的棱长为a,且E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP,BP,CP,DP,M,N分别是AB,BC的中点,以O为原点,
为单位正交基底建立空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若E,F分别为PA,PB的中点,求点A,B,C,D,E,F的坐标.
解 由题意知,点B的坐标为(1,1,0).
由点A与点B关于x轴对称,得A(1,-1,0),
由点C与点B关于y轴对称,得C(-1,1,0),
由点D与点C关于x轴对称,得D(-1,-1,0).
又P(0,0,2),E为AP的中点,F为PB的中点,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在空间直角坐标系中,点M(1,2,3)到z轴的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.(多选)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=4,AA1=3,以直线DA,DC,DD1分别为x轴、y轴、z轴,建立空间直角坐标系,则下列说法正确的是
A.点B1的坐标为(4,5,3)
B.点C1关于点B对称的点为(5,8,-3)
C.点A关于直线BD1对称的点为(0,5,3)
D.点C关于平面ABB1A1对称的点为(8,5,0)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
解析 根据题意知,点B1的坐标为(4,5,3),选项A正确;
B的坐标为(4,5,0),C1的坐标为(0,5,3),
故点C1关于点B对称的点为(8,5,-3),选项B错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以四边形ABC1D1为正方形,AC1与BD1垂直且平分,
即点A关于直线BD1对称的点为C1(0,5,3),选项C正确;
点C关于平面ABB1A1对称的点为(8,5,0),选项D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.(2,1,-3) B.(-1,2,-3)
C.(1,-8,9) D.(-1,8,-9)
√
14.在三棱锥P-ABC中,∠ABC=90°,PB⊥平面ABC,AB=BC=PB=1,M,N分别是PC,AC的中点,建立如图
所示的坐标系Bxyz,则向量 的坐标为______________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知向量p在基底{a,b,c}下的坐标为(2,1,-1),则p在基底{2a,b,-c}下的坐标为________,在基底{a+b,a-b,c}下的坐
标为____________.
(1,1,1)
解析 由题意知p=2a+b-c,
则向量p在基底{2a,b,-c}下的坐标为(1,1,1).
设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则
p=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,
又∵p=2a+b-c,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图所示,正四面体ABCD的棱长为1,G是△BCD的中心,建立如图所示的空间直角坐标系,则 的坐标为
____________, 的坐标为_________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
