第一章 §1.3 1.3.2空间向量运算的坐标表示 课件(共52张PPT)
文档属性
| 名称 | 第一章 §1.3 1.3.2空间向量运算的坐标表示 课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 22:04:20 | ||
图片预览









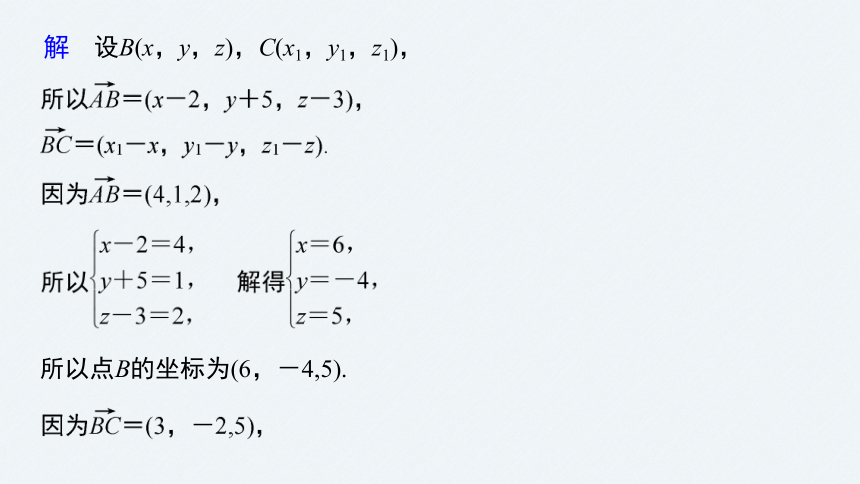

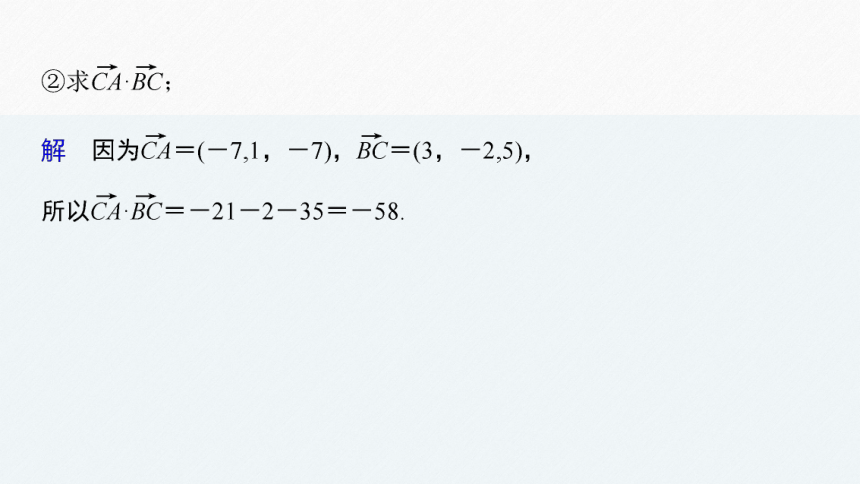
文档简介
(共80张PPT)
1.3.2 空间向量运算的坐标表示
第一章 §1.3 空间向量及其运算的坐标表示
1.掌握空间向量运算的坐标表示.
2.掌握空间两点间的距离公式.
3.会用向量的坐标解决一些简单的几何问题.
学习目标
前面我们通过引入空间直角坐标系,将空间向量的坐标与空间点的坐标一一对应起来.那么有了空间向量的坐标表示,类比平面向量的坐标运算,同学们是否可以探究出空间向量运算的坐标表示并给出证明?
导语
随堂演练
课时对点练
一、空间向量运算的坐标表示
二、空间向量平行、垂直的坐标表示及应用
三、夹角和距离的计算
内容索引
一、空间向量运算的坐标表示
向量运算 向量表示 坐标表示
加法 a+b ______________________
减法 a-b ________________________
数乘 λa ______________
数量积 a·b ________________
设向量a=(a1,a2,a3),b=(b1,b2,b3),λ∈R,那么
(a1+b1,a2+b2,a3+b3)
知识梳理
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
注意点:
(1)空间向量运算的坐标表示与平面向量的坐标表示完全一致.
(2)设A(x1,y1,z1),B(x2,y2,z2),则 =(x2-x1,y2-y1,z2-z1).即一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.
(3)运用公式可以简化运算:(a±b)2=a2±2a·b+b2;(a+b)·(a-b)=a2-b2.
(4)向量线性运算的结果仍是向量,用坐标表示;数量积的结果为数量.
例1 (1)已知a=(-1,2,1),b=(2,0,1),则(2a+3b)·(a-b)=_____.
解析 易得2a+3b=(4,4,5),a-b=(-3,2,0),
则(2a+3b)·(a-b)=4×(-3)+4×2+5×0=-4.
-4
①求顶点B,C的坐标;
解 设B(x,y,z),C(x1,y1,z1),
所以点B的坐标为(6,-4,5).
所以点C的坐标为(9,-6,10).
解 设P(x2,y2,z2),
反思感悟 空间向量坐标运算的规律及注意点
(1)由点的坐标求向量坐标:空间向量的坐标可由其两个端点的坐标确定.
(2)直接计算问题:首先将空间向量用坐标表示出来,然后代入公式计算.
(3)由条件求向量或点的坐标:把向量坐标形式设出来,通过解方程(组),求出其坐标.
4
∴a·b=1+0+3=4.
二、空间向量平行、垂直的坐标表示及应用
设a=(a1,a2,a3),b=(b1,b2,b3),则有
平行关系:当b≠0时,a∥b a=λb , ,________
(λ∈R);
垂直关系:a⊥b a·b=0 .
a1=λb1
a2=λb2
知识梳理
a3=λb3
a1b1+a2b2+a3b3=0
注意点:
(1)要证明a⊥b,就是证明a·b=0;要证明a∥b,就是证明a=λb(b≠0).
所以2a-b=(3,2,-2),
所以2a-b=-2c,
所以(2a-b)∥c.
②若ka+b与ka-2b互相垂直,求k.
所以ka+b=(k-1,k,2),ka-2b=(k+2,k,-4).
又因为(ka+b)⊥(ka-2b),
所以(ka+b)·(ka-2b)=0,
即(k-1,k,2)·(k+2,k,-4)=2k2+k-10=0.
解 如图所示,以点D为原点,
由题意,可设点P的坐标为(a,a,1),
所以3(a-1,a-1,0)=(-a,-a,0),
延伸探究
1.若本例中的PQ⊥AE改为B1Q⊥EQ,其他条件不变,结果如何?
设正方体棱长为1,点Q的坐标为(c,c,0),
因为B1Q⊥EQ,
所以点Q是线段BD的中点,
2.本例中若点G是A1D的中点,点H在平面Dxy上,且GH∥BD1,试判断点H的位置.
设正方体的棱长为1,
因为点G是A1D的中点,
因为点H在平面Dxy上,
设点H的坐标为(m,n,0),
且GH∥BD1,
所以点H为线段AB的中点.
反思感悟 (1)判断两向量是否平行或垂直可直接利用向量平行或垂直的充要条件;已知两向量平行或垂直求参数值,则利用平行、垂直的充要条件,将位置关系转化为坐标关系,列方程(组)求解.
(2)利用向量证明直线、平面平行或垂直,则要建立恰当的空间直角坐标系,求出相关向量的坐标,利用向量平行、垂直的充要条件证明.
跟踪训练2 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= CE=EF=1.
(1)求证:AF∥平面BDE;
证明 设AC与BD交于点G,连接EG.
所以四边形AGEF为平行四边形,
所以AF∥EG.
因为EG 平面BDE,AF 平面BDE,
所以AF∥平面BDE.
(2)求证:CF⊥平面BDE.
证明 因为正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系Cxyz.
即CF⊥BE,CF⊥DE.
又BE∩DE=E,且BE 平面BDE,DE 平面BDE,所以CF⊥平面BDE.
三、夹角和距离的计算
问题 你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
提示 如图,建立空间直角坐标系Oxyz,
设P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,
因此,空间中已知两点A(x1,y1,z1),B(x2,y2,z2),
注意点:
(1)空间两点间的距离公式类似于平面中的两点之间的距离公式,可以类比记忆.
知识梳理
例3 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是AA1,CB1的中点.
(1)求BM,BN的长.
解 以C为原点,以CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
(2)求△BMN的面积.
反思感悟 利用空间向量的坐标运算的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系.
(2)求坐标:①求出相关点的坐标;②写出向量的坐标.
(3)论证、计算:结合公式进行论证、计算.
(4)转化:转化为平行与垂直、夹角与距离问题.
跟踪训练3 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为D1D,BD的中点,G在棱CD上,且CG= H为C1G的中点.
(1)求证:EF⊥B1C;
证明 如图,建立空间直角坐标系Dxyz,D为坐标原点,
(2)求FH的长;
(3)求EF与C1G所成角的余弦值.
1.知识清单:
(1)向量的坐标的运算.
(2)向量的坐标表示的应用.
2.方法归纳:类比、转化.
3.常见误区:
(1)由两向量共线直接得到两向量对应坐标的比相等.
(2)求异面直线所成的角时易忽略范围;讨论向量夹角忽略向量共线的情况.
课堂小结
随堂演练
1.已知M(5,-1,2),A(4,2,-1),O为坐标原点, 则点B的坐标应为
A.(-1,3,-3) B.(9,1,1)
C.(1,-3,3) D.(-9,-1,-1)
√
1
2
3
4
2.已知向量a=(0,-1,1),b=(4,1,0),|λa+b|= 且λ>0,则λ等于
A.5 B.4 C.3 D.2
√
1
2
3
4
解析 λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
3.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是
√
1
2
3
4
解析 依题意得(ka+b)·(2a-b)=0,
所以2k|a|2-ka·b+2a·b-|b|2=0,
而|a|2=2,|b|2=5,a·b=-1,
1
2
3
4
课时对点练
1.已知a=(1,-2,1),a-b=(-1,2,-1),则b等于
A.(2,-4,2) B.(-2,4,-2)
C.(-2,0,-2) D.(2,1,-3)
√
解析 b=a-(-1,2,-1)=(1,-2,1)-(-1,2,-1)=(2,-4,2).
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设点C的坐标为(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
3.已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于
解析 ∵a-b+2c=(9,3,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以△ABC是直角三角形.
5.空间中点A(3,3,1)关于平面Oxy的对称点A′与B(-1,1,5)的长度为
√
解析 点A(3,3,1)关于平面Oxy的对称点A′的坐标为(3,3,-1),
所以A′与B(-1,1,5)的长度为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知向量a=(1,2,3),b=(-2,-4,-6),|c|= 若(a+b)·c=7,则a与c的夹角为
A.30° B.60° C.120° D.150°
√
解析 a+b=(-1,-2,-3)=-a,
故(a+b)·c=-a·c=7,
得a·c=-7,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以〈a,c〉=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以O为坐标原点,OA,OO1所在直线分别为y,z轴建立如图所示的空间直角坐标系Oxyz,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(-1,3,3)
解析 设点P(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
得(x+1,y-3,z-1)=2(-1-x,3-y,4-z),
即P(-1,3,3).
解 由空间两点间的距离公式得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= BC=1,PA=2,E为PD的中点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求AC与PB所成角的余弦值;
解 由题意,建立如图所示的空间直角坐标系,
设AC与PB的夹角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在侧面PAB内找一点N,使NE⊥平面PAC,求N点的坐标.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由于N点在侧面PAB内,
故可设N点坐标为(x,0,z),
11.已知点A(1-t,1-t,t),B(2,t,t),则A,B两点的距离的最小值为
√
解析 因为点A(1-t,1-t,t),B(2,t,t),
所以|AB|2=(1+t)2+(2t-1)2+(t-t)2=5t2-2t+2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.(多选)从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使|PQ|=18,则Q点的坐标为
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以λ=±2,
所以(x0-1,y0-2,z0-3)=±2(-4,-1,8),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a与b的夹角为钝角,
所以a·b<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若a与b的夹角为180°,
则存在λ<0,使a=λb(λ<0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知棱长为a的正四面体ABCD,如图,建立空间直角坐标系,O为A在底面上的射影,M,N分别为线段AB,AD的中点,则M的坐标是
___________________,CN与DM所成角的余弦值为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是______,若D1E⊥EC,则AE=____.
90°
1
解析 在长方体ABCD-A1B1C1D1中,以D为原点,建立如图所示的空间直角坐标系.
又AD=AA1=1,AB=2,点E在棱AB上移动.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0),
设E(1,m,0),0≤m≤2,
∴直线D1E与A1D所成角的大小是90°.
解得m=1,∴AE=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.在正三棱柱ABC-A1B1C1中,△ABC和△A1B1C1为正三角形,所有的棱长都是2,M是BC边的中点,则在棱CC1上是否存在点N,使得异面直线AB1和MN所成的角等于45°?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 以A点为原点,建立如图所示的空间直角坐标系Axyz.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又点N在棱CC1上,可设N(0,2,m)(0≤m≤2),
若异面直线AB1和MN所成的角等于45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以在棱CC1上不存在点N,使得异面直线AB1和MN所成的角等于45°.
1.3.2 空间向量运算的坐标表示
第一章 §1.3 空间向量及其运算的坐标表示
1.掌握空间向量运算的坐标表示.
2.掌握空间两点间的距离公式.
3.会用向量的坐标解决一些简单的几何问题.
学习目标
前面我们通过引入空间直角坐标系,将空间向量的坐标与空间点的坐标一一对应起来.那么有了空间向量的坐标表示,类比平面向量的坐标运算,同学们是否可以探究出空间向量运算的坐标表示并给出证明?
导语
随堂演练
课时对点练
一、空间向量运算的坐标表示
二、空间向量平行、垂直的坐标表示及应用
三、夹角和距离的计算
内容索引
一、空间向量运算的坐标表示
向量运算 向量表示 坐标表示
加法 a+b ______________________
减法 a-b ________________________
数乘 λa ______________
数量积 a·b ________________
设向量a=(a1,a2,a3),b=(b1,b2,b3),λ∈R,那么
(a1+b1,a2+b2,a3+b3)
知识梳理
(a1-b1,a2-b2,a3-b3)
(λa1,λa2,λa3)
a1b1+a2b2+a3b3
注意点:
(1)空间向量运算的坐标表示与平面向量的坐标表示完全一致.
(2)设A(x1,y1,z1),B(x2,y2,z2),则 =(x2-x1,y2-y1,z2-z1).即一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.
(3)运用公式可以简化运算:(a±b)2=a2±2a·b+b2;(a+b)·(a-b)=a2-b2.
(4)向量线性运算的结果仍是向量,用坐标表示;数量积的结果为数量.
例1 (1)已知a=(-1,2,1),b=(2,0,1),则(2a+3b)·(a-b)=_____.
解析 易得2a+3b=(4,4,5),a-b=(-3,2,0),
则(2a+3b)·(a-b)=4×(-3)+4×2+5×0=-4.
-4
①求顶点B,C的坐标;
解 设B(x,y,z),C(x1,y1,z1),
所以点B的坐标为(6,-4,5).
所以点C的坐标为(9,-6,10).
解 设P(x2,y2,z2),
反思感悟 空间向量坐标运算的规律及注意点
(1)由点的坐标求向量坐标:空间向量的坐标可由其两个端点的坐标确定.
(2)直接计算问题:首先将空间向量用坐标表示出来,然后代入公式计算.
(3)由条件求向量或点的坐标:把向量坐标形式设出来,通过解方程(组),求出其坐标.
4
∴a·b=1+0+3=4.
二、空间向量平行、垂直的坐标表示及应用
设a=(a1,a2,a3),b=(b1,b2,b3),则有
平行关系:当b≠0时,a∥b a=λb , ,________
(λ∈R);
垂直关系:a⊥b a·b=0 .
a1=λb1
a2=λb2
知识梳理
a3=λb3
a1b1+a2b2+a3b3=0
注意点:
(1)要证明a⊥b,就是证明a·b=0;要证明a∥b,就是证明a=λb(b≠0).
所以2a-b=(3,2,-2),
所以2a-b=-2c,
所以(2a-b)∥c.
②若ka+b与ka-2b互相垂直,求k.
所以ka+b=(k-1,k,2),ka-2b=(k+2,k,-4).
又因为(ka+b)⊥(ka-2b),
所以(ka+b)·(ka-2b)=0,
即(k-1,k,2)·(k+2,k,-4)=2k2+k-10=0.
解 如图所示,以点D为原点,
由题意,可设点P的坐标为(a,a,1),
所以3(a-1,a-1,0)=(-a,-a,0),
延伸探究
1.若本例中的PQ⊥AE改为B1Q⊥EQ,其他条件不变,结果如何?
设正方体棱长为1,点Q的坐标为(c,c,0),
因为B1Q⊥EQ,
所以点Q是线段BD的中点,
2.本例中若点G是A1D的中点,点H在平面Dxy上,且GH∥BD1,试判断点H的位置.
设正方体的棱长为1,
因为点G是A1D的中点,
因为点H在平面Dxy上,
设点H的坐标为(m,n,0),
且GH∥BD1,
所以点H为线段AB的中点.
反思感悟 (1)判断两向量是否平行或垂直可直接利用向量平行或垂直的充要条件;已知两向量平行或垂直求参数值,则利用平行、垂直的充要条件,将位置关系转化为坐标关系,列方程(组)求解.
(2)利用向量证明直线、平面平行或垂直,则要建立恰当的空间直角坐标系,求出相关向量的坐标,利用向量平行、垂直的充要条件证明.
跟踪训练2 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= CE=EF=1.
(1)求证:AF∥平面BDE;
证明 设AC与BD交于点G,连接EG.
所以四边形AGEF为平行四边形,
所以AF∥EG.
因为EG 平面BDE,AF 平面BDE,
所以AF∥平面BDE.
(2)求证:CF⊥平面BDE.
证明 因为正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系Cxyz.
即CF⊥BE,CF⊥DE.
又BE∩DE=E,且BE 平面BDE,DE 平面BDE,所以CF⊥平面BDE.
三、夹角和距离的计算
问题 你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
提示 如图,建立空间直角坐标系Oxyz,
设P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,
因此,空间中已知两点A(x1,y1,z1),B(x2,y2,z2),
注意点:
(1)空间两点间的距离公式类似于平面中的两点之间的距离公式,可以类比记忆.
知识梳理
例3 如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是AA1,CB1的中点.
(1)求BM,BN的长.
解 以C为原点,以CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
(2)求△BMN的面积.
反思感悟 利用空间向量的坐标运算的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系.
(2)求坐标:①求出相关点的坐标;②写出向量的坐标.
(3)论证、计算:结合公式进行论证、计算.
(4)转化:转化为平行与垂直、夹角与距离问题.
跟踪训练3 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为D1D,BD的中点,G在棱CD上,且CG= H为C1G的中点.
(1)求证:EF⊥B1C;
证明 如图,建立空间直角坐标系Dxyz,D为坐标原点,
(2)求FH的长;
(3)求EF与C1G所成角的余弦值.
1.知识清单:
(1)向量的坐标的运算.
(2)向量的坐标表示的应用.
2.方法归纳:类比、转化.
3.常见误区:
(1)由两向量共线直接得到两向量对应坐标的比相等.
(2)求异面直线所成的角时易忽略范围;讨论向量夹角忽略向量共线的情况.
课堂小结
随堂演练
1.已知M(5,-1,2),A(4,2,-1),O为坐标原点, 则点B的坐标应为
A.(-1,3,-3) B.(9,1,1)
C.(1,-3,3) D.(-9,-1,-1)
√
1
2
3
4
2.已知向量a=(0,-1,1),b=(4,1,0),|λa+b|= 且λ>0,则λ等于
A.5 B.4 C.3 D.2
√
1
2
3
4
解析 λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
3.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是
√
1
2
3
4
解析 依题意得(ka+b)·(2a-b)=0,
所以2k|a|2-ka·b+2a·b-|b|2=0,
而|a|2=2,|b|2=5,a·b=-1,
1
2
3
4
课时对点练
1.已知a=(1,-2,1),a-b=(-1,2,-1),则b等于
A.(2,-4,2) B.(-2,4,-2)
C.(-2,0,-2) D.(2,1,-3)
√
解析 b=a-(-1,2,-1)=(1,-2,1)-(-1,2,-1)=(2,-4,2).
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设点C的坐标为(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
3.已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于
解析 ∵a-b+2c=(9,3,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以△ABC是直角三角形.
5.空间中点A(3,3,1)关于平面Oxy的对称点A′与B(-1,1,5)的长度为
√
解析 点A(3,3,1)关于平面Oxy的对称点A′的坐标为(3,3,-1),
所以A′与B(-1,1,5)的长度为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知向量a=(1,2,3),b=(-2,-4,-6),|c|= 若(a+b)·c=7,则a与c的夹角为
A.30° B.60° C.120° D.150°
√
解析 a+b=(-1,-2,-3)=-a,
故(a+b)·c=-a·c=7,
得a·c=-7,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以〈a,c〉=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以O为坐标原点,OA,OO1所在直线分别为y,z轴建立如图所示的空间直角坐标系Oxyz,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(-1,3,3)
解析 设点P(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
得(x+1,y-3,z-1)=2(-1-x,3-y,4-z),
即P(-1,3,3).
解 由空间两点间的距离公式得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= BC=1,PA=2,E为PD的中点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求AC与PB所成角的余弦值;
解 由题意,建立如图所示的空间直角坐标系,
设AC与PB的夹角为θ,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)在侧面PAB内找一点N,使NE⊥平面PAC,求N点的坐标.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 由于N点在侧面PAB内,
故可设N点坐标为(x,0,z),
11.已知点A(1-t,1-t,t),B(2,t,t),则A,B两点的距离的最小值为
√
解析 因为点A(1-t,1-t,t),B(2,t,t),
所以|AB|2=(1+t)2+(2t-1)2+(t-t)2=5t2-2t+2,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
12.(多选)从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使|PQ|=18,则Q点的坐标为
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以λ=±2,
所以(x0-1,y0-2,z0-3)=±2(-4,-1,8),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a与b的夹角为钝角,
所以a·b<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若a与b的夹角为180°,
则存在λ<0,使a=λb(λ<0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知棱长为a的正四面体ABCD,如图,建立空间直角坐标系,O为A在底面上的射影,M,N分别为线段AB,AD的中点,则M的坐标是
___________________,CN与DM所成角的余弦值为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是______,若D1E⊥EC,则AE=____.
90°
1
解析 在长方体ABCD-A1B1C1D1中,以D为原点,建立如图所示的空间直角坐标系.
又AD=AA1=1,AB=2,点E在棱AB上移动.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0),
设E(1,m,0),0≤m≤2,
∴直线D1E与A1D所成角的大小是90°.
解得m=1,∴AE=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.在正三棱柱ABC-A1B1C1中,△ABC和△A1B1C1为正三角形,所有的棱长都是2,M是BC边的中点,则在棱CC1上是否存在点N,使得异面直线AB1和MN所成的角等于45°?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 以A点为原点,建立如图所示的空间直角坐标系Axyz.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
又点N在棱CC1上,可设N(0,2,m)(0≤m≤2),
若异面直线AB1和MN所成的角等于45°,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以在棱CC1上不存在点N,使得异面直线AB1和MN所成的角等于45°.
