第一章 §1.4 1.4.2 第1课时 距离问题 课件(共66张PPT)
文档属性
| 名称 | 第一章 §1.4 1.4.2 第1课时 距离问题 课件(共66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-01 00:00:00 | ||
图片预览






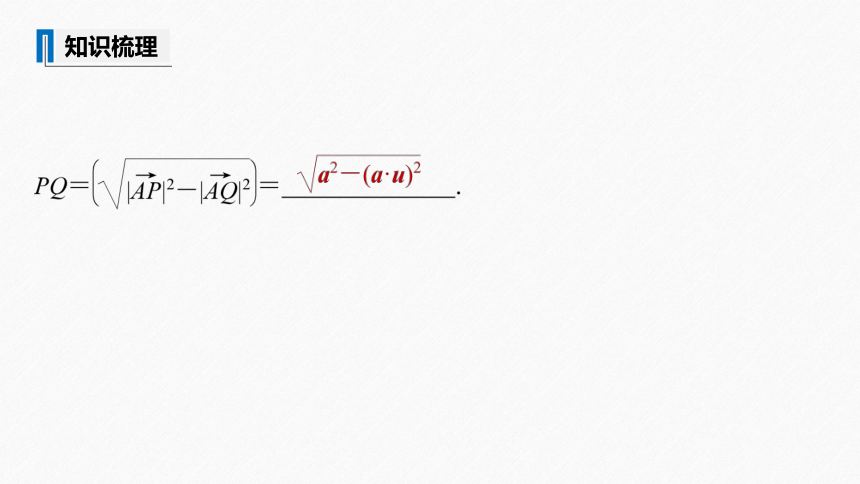

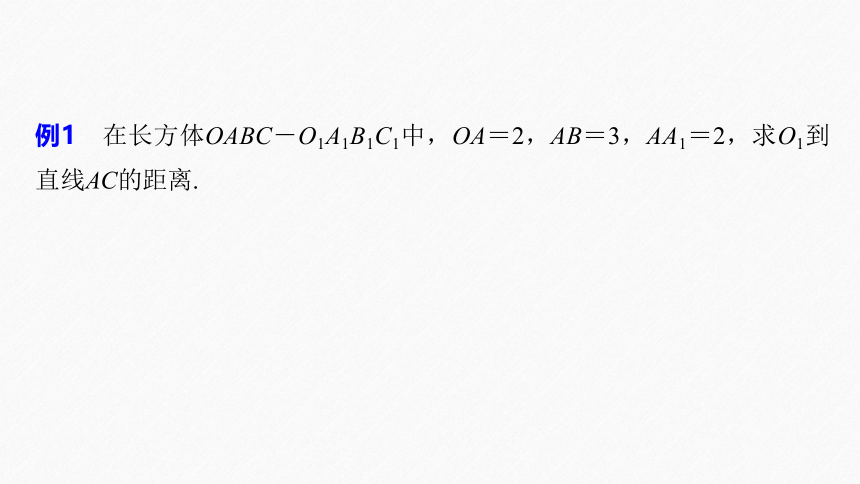


文档简介
(共66张PPT)
第1课时 距离问题
第一章 1.4.2 用空间向量研究距离、夹角问题
1.能用向量方法解决点到直线、点到平面、相互平行的直线、相互
平行的平面间的距离问题.
2.通过空间中距离问题的求解,体会向量方法在研究几何问题中的
作用.
学习目标
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库.如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
导语
随堂演练
课时对点练
一、点到直线的距离
二、点到平面的距离与直线到平面的距离
内容索引
一、点到直线的距离
问题1 如图,已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
知识梳理
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
提示 在其中一条直线上取定一点,则该点到另一条直线的距离即为两条平行直线之间的距离.
例1 在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,求O1到直线AC的距离.
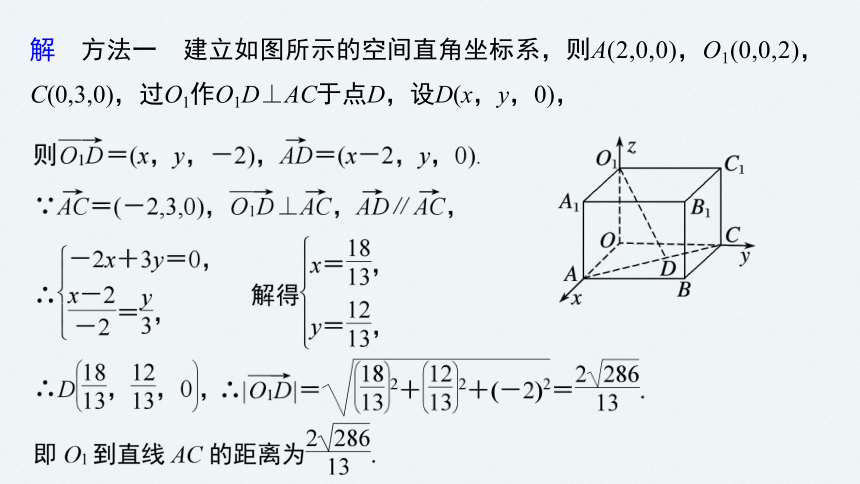
解 方法一 建立如图所示的空间直角坐标系,则A(2,0,0),O1(0,0,2),C(0,3,0),过O1作O1D⊥AC于点D,设D(x,y,0),
方法二 连接AO1,建立如图所示的空间直角坐标系,
则A(2,0,0),O1(0,0,2),C(0,3,0),
反思感悟 用向量法求点到直线的距离的一般步骤
(1)求直线的方向向量.
(2)计算所求点与直线上某一点所构成的向量在直线的方向向量上的投影向量的长度.
(3)利用勾股定理求解.另外,要注意平行直线间的距离与点到直线的距离之间的转化.
跟踪训练1 如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB=3,AD=4,PA=1,求点P到BD的距离.
解 如图,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,1),B(3,0,0),D(0,4,0),
二、点到平面的距离与直线到平面的距离
问题3 已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.如何求平面α外一点P到平面α的距离?
提示 过点P作平面α的垂线l,交平面α于点Q,
PQ= .
知识梳理
注意点:
(1)实质上,n是直线l的方向向量,点P到平面α的距离就是 在直线l上的投影向量 的长度.
(2)如果一条直线l与一个平面α平行,可在直线l上任取一点P,将线面距离转化为点P到平面α的距离求解.
(3)如果两个平面α,β互相平行,在其中一个平面α内任取一点P,可将两个平行平面的距离转化为点P到平面β的距离求解.
例2 如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.
(1)求点D到平面PEF的距离;
解 建立如图所示的空间直角坐标系,
则D(0,0,0),P(0,0,1),A(1,0,0),
设DH⊥平面PEF,垂足为H,则
(2)求直线AC到平面PEF的距离.
解 由题意得,AC∥EF,直线AC到平面PEF的距离即为点A到平面PEF的距离,
平面PEF的一个法向量为n=(2,2,3),
反思感悟 用向量法求点面距离的步骤
(1)建系:建立恰当的空间直角坐标系.
(2)求点坐标:写出(求出)相关点的坐标.
(3)求向量:求出相关向量的坐标( α内两不共线向量,平面α的法向量n).
跟踪训练2 如图所示,已知四棱柱ABCD-A1B1C1D1是底面边长为1的正四棱柱.若点C到平面AB1D1的距离为 求正四棱柱ABCD-A1B1C1D1
的高.
解 设正四棱柱的高为h(h>0),建立如图所示的空间直角坐标系,有A(0,0,h),B1(1,0,0),D1(0,1,0),C(1,1,h),
设平面AB1D1的法向量为n=(x,y,z),
取z=1,得n=(h,h,1),
解得h=2.
故正四棱柱ABCD-A1B1C1D1的高为2.
1.知识清单:
(1)点到直线的距离.
(2)点到平面的距离与直线到平面的距离.
2.方法归纳:数形结合、转化法.
3.常见误区:对距离公式理解不到位,在使用时生硬套用.对公式推导过程的理解是应用的基础.
课堂小结
随堂演练
解析 ∵A(0,0,2),B(1,0,2),C(0,2,0),
∴点A到直线BC的距离为
1.已知A(0,0,2),B(1,0,2),C(0,2,0),则点A到直线BC的距离为
√
1
2
3
4
2.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是
√
1
2
3
4
解析 分别以PA,PB,PC所在直线为x轴,y轴,z轴建立空间直角坐标系,
则A(1,0,0),B(0,1,0),C(0,0,1).
可以求得平面ABC的一个法向量为n=(1,1,1),
3.已知棱长为1的正方体ABCD-A1B1C1D1,则平面AB1C与平面A1C1D之间的距离为
√
1
2
3
4
1
2
3
4
解析 建立如图所示的空间直角坐标系,
则A1(1,0,0),C1(0,1,0),D(0,0,1),A(1,0,1),
设平面A1C1D的一个法向量为m=(x,y,1),
故m=(1,1,1),
显然平面AB1C∥平面A1C1D,
4.已知直线l经过点A(2,3,1),且向量n=(1,0,-1)所在直线与l垂直,则点
P(4,3,2)到l的距离为____.
1
2
3
4
课时对点练
1.在长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a,则点D1到直线AC的距离为
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 连接BD,AC交于点O(图略),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 如图建立空间直角坐标系,易得C(a,a,0),D1(0,a,2a),
2.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是
√
解析 ∵两平行平面α,β分别经过坐标原点O和点A(2,1,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知三棱锥O-ABC中,OA⊥OB,OB⊥OC,OC⊥OA,且OA=1,OB=2,OC=2,则点A到直线BC的距离为
√
解析 以O为坐标原点,建立如图所示的空间直角坐标系.
由题意可知A(1,0,0),B(0,2,0),C(0,0,2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如图,已知长方体ABCD-A1B1C1D1中,A1A=5,AB=12,则直线B1C1到平面A1BCD1的距离是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以D为坐标原点, 的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,
则C(0,12,0),D1(0,0,5).
设B(x,12,0),B1(x,12,5)(x>0).
设平面A1BCD1的法向量为n=(a,b,c),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为B1C1∥平面A1BCD1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则B1(2,2,0),C1(0,2,0),E(2,1,2),F(1,2,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面B1EF的法向量为n=(x,y,z),
令z=1,得n=(2,2,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.Rt△ABC的两条直角边BC=3,AC=4,PC⊥平面ABC,PC= 则点P到斜边AB的距离是________.
3
解析 以C为坐标原点,CA,CB,CP为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A(4,0,0),B(0,3,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑(bie nao),如图.已知在鳖臑P-ABC中,PA⊥平面ABC,PA=AB=BC=2,M为PC的中点,则点P到平面MAB的距离为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以B为坐标原点,BA,BC所在直线分别为x轴、y轴建立空间直角坐标系,
如图,则B(0,0,0),A(2,0,0),P(2,0,2),C(0,2,0),由M为PC的中点可得M(1,1,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设n=(x,y,z)为平面ABM的一个法向量,
9.在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;
解 建立如图所示的空间直角坐标系,
则A(0,0,0),A1(0,0,2),M(2,0,1),C1(0,2,2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求点N到平面MA1C1的距离.
解 设平面MA1C1的一个法向量为n=(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
取x=1,得z=2,故n=(1,0,2)为平面MA1C1的一个法向量,因为N(1,1,0),
10.在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AD=2AB=4,且PD与底面ABCD所成的角为45°.求点B到直线PD的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ∵PA⊥平面ABCD,
∴∠PDA即为PD与平面ABCD所成的角,
∴∠PDA=45°,
∴PA=AD=4,AB=2.
以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设E(x,y,z),
∴(x,y-4,z)=λ(0,-4,4),∴x=0,y=4-4λ,z=4λ,
∵BE⊥DP,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以点B到直线PD的距离为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.如图,ABCD-EFGH是棱长为1的正方体,若P在正方体内部且满足
则P到AB的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
解析 如图,分别以AB,AD,AE所在直线为x,y,z轴建立空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设点N为ME的中点,则点N到平面D1EF的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系(图略),
则M(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面D1EF的一个法向量为n=(x,y,z),
取x=1,得n=(1,0,2),
13.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的
中点,则直线MN到平面ACD1的距离为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面ACD1的一个法向量为n=(x,y,z),
令x=1,则y=z=1,∴n=(1,1,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故MN∥平面ACD1,
14.如图,在三棱柱ABC-A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,
则点B1到平面ABC1的距离为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 建立如图所示的空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面ABC1的一个法向量为n=(x,y,1),
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 取AC的中点D,建立如图所示的空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以点C到直线AB1的距离
16.如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,CA=2,侧棱AA1=2,D是CC1的中点,则在线段A1B上是否存在一点E(异于A1,B两点),使得点A1到平面AED的距离为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 假设存在点E满足题意.以点C为坐标原点,CA,CB,CC1所在的直线分别为x轴,y轴和z轴建立如图所示的空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则E(2λ,2(1-λ),2λ),
设n=(x,y,z)为平面AED的一个法向量,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
第1课时 距离问题
第一章 1.4.2 用空间向量研究距离、夹角问题
1.能用向量方法解决点到直线、点到平面、相互平行的直线、相互
平行的平面间的距离问题.
2.通过空间中距离问题的求解,体会向量方法在研究几何问题中的
作用.
学习目标
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库.如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
导语
随堂演练
课时对点练
一、点到直线的距离
二、点到平面的距离与直线到平面的距离
内容索引
一、点到直线的距离
问题1 如图,已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离?
知识梳理
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
提示 在其中一条直线上取定一点,则该点到另一条直线的距离即为两条平行直线之间的距离.
例1 在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,求O1到直线AC的距离.
解 方法一 建立如图所示的空间直角坐标系,则A(2,0,0),O1(0,0,2),C(0,3,0),过O1作O1D⊥AC于点D,设D(x,y,0),
方法二 连接AO1,建立如图所示的空间直角坐标系,
则A(2,0,0),O1(0,0,2),C(0,3,0),
反思感悟 用向量法求点到直线的距离的一般步骤
(1)求直线的方向向量.
(2)计算所求点与直线上某一点所构成的向量在直线的方向向量上的投影向量的长度.
(3)利用勾股定理求解.另外,要注意平行直线间的距离与点到直线的距离之间的转化.
跟踪训练1 如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB=3,AD=4,PA=1,求点P到BD的距离.
解 如图,分别以AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,1),B(3,0,0),D(0,4,0),
二、点到平面的距离与直线到平面的距离
问题3 已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点.如何求平面α外一点P到平面α的距离?
提示 过点P作平面α的垂线l,交平面α于点Q,
PQ= .
知识梳理
注意点:
(1)实质上,n是直线l的方向向量,点P到平面α的距离就是 在直线l上的投影向量 的长度.
(2)如果一条直线l与一个平面α平行,可在直线l上任取一点P,将线面距离转化为点P到平面α的距离求解.
(3)如果两个平面α,β互相平行,在其中一个平面α内任取一点P,可将两个平行平面的距离转化为点P到平面β的距离求解.
例2 如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.
(1)求点D到平面PEF的距离;
解 建立如图所示的空间直角坐标系,
则D(0,0,0),P(0,0,1),A(1,0,0),
设DH⊥平面PEF,垂足为H,则
(2)求直线AC到平面PEF的距离.
解 由题意得,AC∥EF,直线AC到平面PEF的距离即为点A到平面PEF的距离,
平面PEF的一个法向量为n=(2,2,3),
反思感悟 用向量法求点面距离的步骤
(1)建系:建立恰当的空间直角坐标系.
(2)求点坐标:写出(求出)相关点的坐标.
(3)求向量:求出相关向量的坐标( α内两不共线向量,平面α的法向量n).
跟踪训练2 如图所示,已知四棱柱ABCD-A1B1C1D1是底面边长为1的正四棱柱.若点C到平面AB1D1的距离为 求正四棱柱ABCD-A1B1C1D1
的高.
解 设正四棱柱的高为h(h>0),建立如图所示的空间直角坐标系,有A(0,0,h),B1(1,0,0),D1(0,1,0),C(1,1,h),
设平面AB1D1的法向量为n=(x,y,z),
取z=1,得n=(h,h,1),
解得h=2.
故正四棱柱ABCD-A1B1C1D1的高为2.
1.知识清单:
(1)点到直线的距离.
(2)点到平面的距离与直线到平面的距离.
2.方法归纳:数形结合、转化法.
3.常见误区:对距离公式理解不到位,在使用时生硬套用.对公式推导过程的理解是应用的基础.
课堂小结
随堂演练
解析 ∵A(0,0,2),B(1,0,2),C(0,2,0),
∴点A到直线BC的距离为
1.已知A(0,0,2),B(1,0,2),C(0,2,0),则点A到直线BC的距离为
√
1
2
3
4
2.若三棱锥P-ABC的三条侧棱两两垂直,且满足PA=PB=PC=1,则点P到平面ABC的距离是
√
1
2
3
4
解析 分别以PA,PB,PC所在直线为x轴,y轴,z轴建立空间直角坐标系,
则A(1,0,0),B(0,1,0),C(0,0,1).
可以求得平面ABC的一个法向量为n=(1,1,1),
3.已知棱长为1的正方体ABCD-A1B1C1D1,则平面AB1C与平面A1C1D之间的距离为
√
1
2
3
4
1
2
3
4
解析 建立如图所示的空间直角坐标系,
则A1(1,0,0),C1(0,1,0),D(0,0,1),A(1,0,1),
设平面A1C1D的一个法向量为m=(x,y,1),
故m=(1,1,1),
显然平面AB1C∥平面A1C1D,
4.已知直线l经过点A(2,3,1),且向量n=(1,0,-1)所在直线与l垂直,则点
P(4,3,2)到l的距离为____.
1
2
3
4
课时对点练
1.在长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a,则点D1到直线AC的距离为
√
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 方法一 连接BD,AC交于点O(图略),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
方法二 如图建立空间直角坐标系,易得C(a,a,0),D1(0,a,2a),
2.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是
√
解析 ∵两平行平面α,β分别经过坐标原点O和点A(2,1,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知三棱锥O-ABC中,OA⊥OB,OB⊥OC,OC⊥OA,且OA=1,OB=2,OC=2,则点A到直线BC的距离为
√
解析 以O为坐标原点,建立如图所示的空间直角坐标系.
由题意可知A(1,0,0),B(0,2,0),C(0,0,2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.如图,已知长方体ABCD-A1B1C1D1中,A1A=5,AB=12,则直线B1C1到平面A1BCD1的距离是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以D为坐标原点, 的方向分别为x,y,z轴的正方向建立如图所示的空间直角坐标系,
则C(0,12,0),D1(0,0,5).
设B(x,12,0),B1(x,12,5)(x>0).
设平面A1BCD1的法向量为n=(a,b,c),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为B1C1∥平面A1BCD1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离等于
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则B1(2,2,0),C1(0,2,0),E(2,1,2),F(1,2,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面B1EF的法向量为n=(x,y,z),
令z=1,得n=(2,2,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.Rt△ABC的两条直角边BC=3,AC=4,PC⊥平面ABC,PC= 则点P到斜边AB的距离是________.
3
解析 以C为坐标原点,CA,CB,CP为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A(4,0,0),B(0,3,0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑(bie nao),如图.已知在鳖臑P-ABC中,PA⊥平面ABC,PA=AB=BC=2,M为PC的中点,则点P到平面MAB的距离为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以B为坐标原点,BA,BC所在直线分别为x轴、y轴建立空间直角坐标系,
如图,则B(0,0,0),A(2,0,0),P(2,0,2),C(0,2,0),由M为PC的中点可得M(1,1,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设n=(x,y,z)为平面ABM的一个法向量,
9.在直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,M为BB1的中点,N为BC的中点.
(1)求点M到直线AC1的距离;
解 建立如图所示的空间直角坐标系,
则A(0,0,0),A1(0,0,2),M(2,0,1),C1(0,2,2),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求点N到平面MA1C1的距离.
解 设平面MA1C1的一个法向量为n=(x,y,z),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
取x=1,得z=2,故n=(1,0,2)为平面MA1C1的一个法向量,因为N(1,1,0),
10.在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AD=2AB=4,且PD与底面ABCD所成的角为45°.求点B到直线PD的距离.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 ∵PA⊥平面ABCD,
∴∠PDA即为PD与平面ABCD所成的角,
∴∠PDA=45°,
∴PA=AD=4,AB=2.
以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设E(x,y,z),
∴(x,y-4,z)=λ(0,-4,4),∴x=0,y=4-4λ,z=4λ,
∵BE⊥DP,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以点B到直线PD的距离为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.如图,ABCD-EFGH是棱长为1的正方体,若P在正方体内部且满足
则P到AB的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
解析 如图,分别以AB,AD,AE所在直线为x,y,z轴建立空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设点N为ME的中点,则点N到平面D1EF的距离为
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系(图略),
则M(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面D1EF的一个法向量为n=(x,y,z),
取x=1,得n=(1,0,2),
13.棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的
中点,则直线MN到平面ACD1的距离为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面ACD1的一个法向量为n=(x,y,z),
令x=1,则y=z=1,∴n=(1,1,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故MN∥平面ACD1,
14.如图,在三棱柱ABC-A1B1C1中,所有棱长均为1,且AA1⊥底面ABC,
则点B1到平面ABC1的距离为________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 建立如图所示的空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设平面ABC1的一个法向量为n=(x,y,1),
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 取AC的中点D,建立如图所示的空间直角坐标系,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以点C到直线AB1的距离
16.如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,CA=2,侧棱AA1=2,D是CC1的中点,则在线段A1B上是否存在一点E(异于A1,B两点),使得点A1到平面AED的距离为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 假设存在点E满足题意.以点C为坐标原点,CA,CB,CC1所在的直线分别为x轴,y轴和z轴建立如图所示的空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则E(2λ,2(1-λ),2λ),
设n=(x,y,z)为平面AED的一个法向量,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
