第五章 5.1.1 变化率问题 课件(共63张PPT)
文档属性
| 名称 | 第五章 5.1.1 变化率问题 课件(共63张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 07:28:00 | ||
图片预览











文档简介
(共63张PPT)
5.1.1 变化率问题
第五章 §5.1 导数的概念及其意义
1.通过实例分析,经历由平均速度过渡到瞬时速度的过程.
2.理解割线的斜率与切线的斜率之间的关系.
3.体会极限思想.
学习目标
同学们,大家知道,在高速路上经常看到“区间测速”这样的提醒,这其实是在提醒司机安全驾驶,其实它测速的方式是在固定的路程上,看你用了多少时间,从而达到测速的目的;大家也经常能听到家长们讨论车辆油耗的问题,你的车几个油?这里所说的几个油实际上是汽车百公里的油耗,不过有些车上可以查看汽车的瞬时油耗,今天我们就来研究生活中的变化率问题.
导语
随堂演练
课时对点练
一、平均速度
二、瞬时速度
三、抛物线的切线的斜率
内容索引
一、平均速度
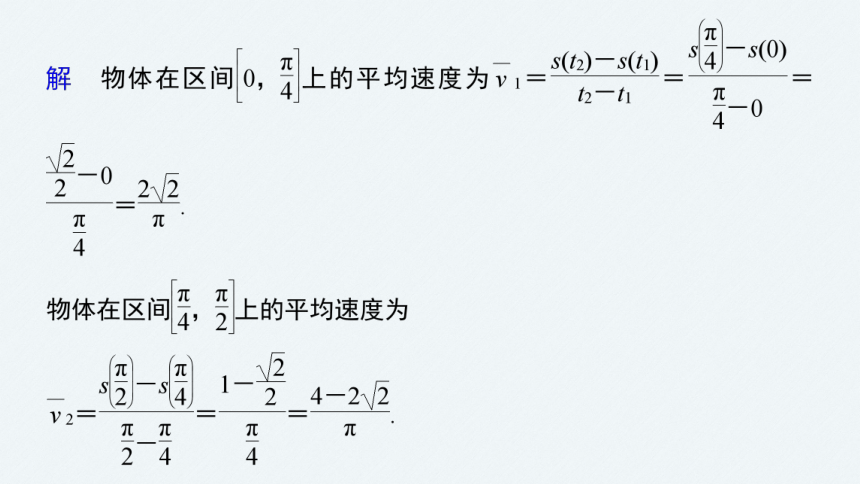
问题1 在高台跳水中,运动员相对于水面的高度h与起跳后的时间存在函数关系h(t)=-4.9t2+6.5t+10,根据上述探究,你能求该运动员在0≤t≤0.5,1≤t≤2,0≤t≤ 内的平均速度吗?
虽然运动员在0≤t≤ 这段时间里的平均速度是0 m/s,
但实际情况是,该运动员仍在运动,可以说明平均速度不能精确描述运动员的运动状态.
(2)比较(1)中两个平均速度的大小,说明其几何意义.
反思感悟 求物体运动的平均速度的主要步骤
(1)先计算位移的改变量s(t2)-s(t1),
(2)再计算时间的改变量t2-t1,
√
二、瞬时速度
问题2 我们也发现了高速路上区间测速的弊端,因为如果某人发现超速了,他只需踩下刹车,让车辆低速行驶一段时间即可,你认为,我们应该如何改进高速路上的区间测速问题?
我们把函数值的增量f(t2)-f(t1)记为Δy,即Δy=f(t2)-f(t1),自变量的增量t2-t1记为Δt,即Δt=t2-t1,
这里的Δt可以看成是t1的一个增量,可用t1+Δt来表示t2,
我们发现如果时间的增量Δt无限小,
此时在极短的时间内的平均速度就可近似等于在时间t=t1的瞬时速度,
这就需要用到我们数学中的“极限”思想,意思就是让Δt无限趋近于0.
知识梳理
1.瞬时速度:物体在 的速度称为瞬时速度.
2.瞬时速度的计算:设物体运动的时间与位移的函数关系式为y=h(t),
则物体在t0时刻的瞬时速度为 .
3.瞬时速度与平均速度的关系:从物理角度看,当时间间隔|Δt|无限趋近于0时,平均速度 就无限趋近于t=t0时的瞬时速度.
注意点:Δt可正,可负,但不能为0.
某一时刻
例2 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
即物体在t=1 s时的瞬时速度为3 m/s.
延伸探究
1.若本例中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度,
=1+Δt,
即物体的初速度为1 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
2.若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
反思感悟 求运动物体瞬时速度的三个步骤
(1)求位移改变量Δs=s(t0+Δt)-s(t0).
跟踪训练2 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2 s时的瞬时速度即为函数在t=2处的瞬时变化率.
∵质点M在t=2附近的平均变化率为
即a=2.
三、抛物线的切线的斜率
问题3 前面我们从物理的角度研究了瞬时速度的问题,它反映到我们几何上是什么意思?
知识梳理
1.切线:设P0是曲线上一定点,P是曲线上的动点,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线在点P0处的切线.
2.切线的斜率:设P0(x0,y0)是曲线y=f(x)上一点,则曲线y=f(x)在点
P0(x0,y0)处的切线的斜率为k0= .
3.切线的斜率与割线的斜率的关系:从几何图形上看,当横坐标间隔|Δx|无限变小时,点P无限趋近于点P0,于是割线PP0无限趋近于点P0处的切线P0T,这时,割线PP0的斜率k无限趋近于点P0处的切线P0T的斜率k0.
注意点:极限的几何意义:曲线y=f(x)在x=x0处的切线斜率.
例3 求抛物线f(x)=x2-2x+3在点(1,2)处的切线方程.
所以切线的方程为y-2=0×(x-1),即y=2.
延伸探究 本例函数不变,求与2x-y+4=0平行的该曲线的切线方程.
=2x0-2+Δx,
故有2x0-2=2,解得x0=2,
所以切点为(2,3),所求切线方程为2x-y-1=0.
反思感悟 (1)求抛物线在某点处的切线方程的步骤
(2)求曲线过某点的切线方程需注意,该点不一定是切点,需另设切点坐标.
跟踪训练3 求抛物线f(x)=x2-x在点(2,2)处的切线方程.
解 f(2+Δx)-f(2)=(2+Δx)2-(2+Δx)-2
=3Δx+(Δx)2,
则切线方程为y-2=3(x-2),即3x-y-4=0.
1.知识清单:
(1)平均速度.
(2)瞬时速度.
(3)曲线在某点处的切线方程.
2.方法归纳:极限法、定义法.
3.常见误区:对割线的斜率与切线的斜率之间的关系理解不到位.
课堂小结
随堂演练
1
2
3
4
1.某质点的运动方程为s(t)=1-t2,则该物体在[1,2]内的平均速度为
A.2 B.3 C.-2 D.-3
√
1
2
3
4
2.一个物体做直线运动,位移s与时间t之间的函数关系式为s(t)=t2+2t+3,则该物体在t=2时的瞬时速度为
A.4 B.5 C.6 D.7
√
1
2
3
4
3.一物体做直线运动,其运动方程为s(t)=-t2+2t,则t=0时,其速度为
A.-2 B.-1 C.0 D.2
所以当t=0时,其速度为2.
√
1
2
3
4
4.抛物线y=x2+4在点(1,5)处的切线的斜率为_____.
2
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.已知抛物线y=3x-x2在x0=2处的增量为Δx=0.1,则 的值为
A.-0.11 B.-1.1 C.3.89 D.0.29
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵Δy=f(2+0.1)-f(2)=(3×2.1-2.12)-(3×2-22)=-0.11,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知函数f(x)=2x2-4的图象上两点A,B,且xA=1,xB=1.1,则函数f(x)从A点到B点的平均变化率为
A.4 B.4x C.4.2 D.4.02
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由瞬时速度与平均速度的关系可知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5.已知曲线y=2x2上一点A(2,8),则在点A处的切线斜率为
A.4 B.16 C.8 D.2
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知某物体的运动方程为s(t)=7t2+8(0≤t≤5),则
A.该物体在1≤t≤3时的平均速度是28
B.该物体在t=4时的瞬时速度是56
C.该物体位移的最大值为43
D.该物体在t=5时的瞬时速度是70
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 该物体在1≤t≤3时的平均速度是
物体的最大位移是7×52+8=183,C错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一做直线运动的物体,其位移s与时间t的关系是s=3t-t2,则物体的初速度是_____.
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.若抛物线f(x)=4x2在点(x0,f(x0))处切线的斜率为8,则x0=_____.
1
解得x0=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某物体按照s(t)=3t2+2t+4(s的单位:m)的规律做直线运动,求自运动开始到4 s时物体运动的平均速度和4 s时的瞬时速度.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 自运动开始到t s时,物体运动的平均速度
由于Δs=3(t+Δt)2+2(t+Δt)+4-(3t2+2t+4)
=(2+6t)Δt+3(Δt)2.
所以4 s时物体的瞬时速度为26 m/s.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.曲线f(x)=x2上哪一点处的切线满足下列条件?
(1)平行于直线y=4x-5;
解 设P(x0,y0)是满足条件的点,曲线f(x)=x2在点P(x0,y0)处切线的斜率为
∵切线与直线y=4x-5平行,∴2x0=4,x0=2,
y0=4,即P(2,4)是满足条件的点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)垂直于直线2x-6y+5=0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)倾斜角为135°.
解 因为切线的倾斜角为135°,
所以其斜率为-1,即2x0=-1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设直线O′A,AB,BC的斜率分别为kO′A,kAB,kBC,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
√
解析 由题意可知
解得a=1,又(0,b)在切线上,∴b=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.A,B两机关开展节能活动,活动开始后两机关的用电量W1(t),W2(t)与时间t(天)的关系如图所示,则一定有
A.两机关节能效果一样好
B.A机关比B机关节能效果好
C.A机关的用电量在[0,t0]上的平均变化率比B机关的用电量在[0,t0]上
的平均变化率大
D.A机关与B机关自节能以来用电量总是一样大
√
解析 由题图可知,A,B两机关用电量在[0,t0]上的平均变化率都小于0,由平均变化率的几何意义知,A机关用电量在[0,t0]上的平均变化率小于B机关的平均变化率,从而A机关比B机关节能效果好.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.函数f(x)=x2-x在区间[-2,t]上的平均变化率是2,则t=_____.
5
解析 因为函数f(x)=x2-x在区间[-2,t]上的平均变化率是2,
即t2-t-6=2t+4,
从而t2-3t-10=0,
解得t=5或t=-2(舍去).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.将半径为R的球加热,若半径从R=1到R=m时球的体积膨胀率为 ,则m的值为_____.
2
所以m2+m+1=7,所以m=2或m=-3(舍).
16.若一物体运动方程如下:(位移单位:m,时间单位:s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
求:(1)物体在t∈[3,5]内的平均速度;
解 ∵物体在t∈[3,5]上的时间变化量为Δt=5-3=2,
物体在t∈[3,5]上的位移变化量为
Δs=3×52+2-(3×32+2)=3×(52-32)=48,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴物体在t∈[3,5]上的平均速度为24 m/s.
(2)物体的初速度v0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 求物体的初速度v0,即求物体在t=0时的瞬时速度.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)物体在t=1时的瞬时速度.
∴物体在t=1时的瞬时速度为
5.1.1 变化率问题
第五章 §5.1 导数的概念及其意义
1.通过实例分析,经历由平均速度过渡到瞬时速度的过程.
2.理解割线的斜率与切线的斜率之间的关系.
3.体会极限思想.
学习目标
同学们,大家知道,在高速路上经常看到“区间测速”这样的提醒,这其实是在提醒司机安全驾驶,其实它测速的方式是在固定的路程上,看你用了多少时间,从而达到测速的目的;大家也经常能听到家长们讨论车辆油耗的问题,你的车几个油?这里所说的几个油实际上是汽车百公里的油耗,不过有些车上可以查看汽车的瞬时油耗,今天我们就来研究生活中的变化率问题.
导语
随堂演练
课时对点练
一、平均速度
二、瞬时速度
三、抛物线的切线的斜率
内容索引
一、平均速度
问题1 在高台跳水中,运动员相对于水面的高度h与起跳后的时间存在函数关系h(t)=-4.9t2+6.5t+10,根据上述探究,你能求该运动员在0≤t≤0.5,1≤t≤2,0≤t≤ 内的平均速度吗?
虽然运动员在0≤t≤ 这段时间里的平均速度是0 m/s,
但实际情况是,该运动员仍在运动,可以说明平均速度不能精确描述运动员的运动状态.
(2)比较(1)中两个平均速度的大小,说明其几何意义.
反思感悟 求物体运动的平均速度的主要步骤
(1)先计算位移的改变量s(t2)-s(t1),
(2)再计算时间的改变量t2-t1,
√
二、瞬时速度
问题2 我们也发现了高速路上区间测速的弊端,因为如果某人发现超速了,他只需踩下刹车,让车辆低速行驶一段时间即可,你认为,我们应该如何改进高速路上的区间测速问题?
我们把函数值的增量f(t2)-f(t1)记为Δy,即Δy=f(t2)-f(t1),自变量的增量t2-t1记为Δt,即Δt=t2-t1,
这里的Δt可以看成是t1的一个增量,可用t1+Δt来表示t2,
我们发现如果时间的增量Δt无限小,
此时在极短的时间内的平均速度就可近似等于在时间t=t1的瞬时速度,
这就需要用到我们数学中的“极限”思想,意思就是让Δt无限趋近于0.
知识梳理
1.瞬时速度:物体在 的速度称为瞬时速度.
2.瞬时速度的计算:设物体运动的时间与位移的函数关系式为y=h(t),
则物体在t0时刻的瞬时速度为 .
3.瞬时速度与平均速度的关系:从物理角度看,当时间间隔|Δt|无限趋近于0时,平均速度 就无限趋近于t=t0时的瞬时速度.
注意点:Δt可正,可负,但不能为0.
某一时刻
例2 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
即物体在t=1 s时的瞬时速度为3 m/s.
延伸探究
1.若本例中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度,
=1+Δt,
即物体的初速度为1 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
2.若本例中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
反思感悟 求运动物体瞬时速度的三个步骤
(1)求位移改变量Δs=s(t0+Δt)-s(t0).
跟踪训练2 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2 s时的瞬时速度即为函数在t=2处的瞬时变化率.
∵质点M在t=2附近的平均变化率为
即a=2.
三、抛物线的切线的斜率
问题3 前面我们从物理的角度研究了瞬时速度的问题,它反映到我们几何上是什么意思?
知识梳理
1.切线:设P0是曲线上一定点,P是曲线上的动点,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线在点P0处的切线.
2.切线的斜率:设P0(x0,y0)是曲线y=f(x)上一点,则曲线y=f(x)在点
P0(x0,y0)处的切线的斜率为k0= .
3.切线的斜率与割线的斜率的关系:从几何图形上看,当横坐标间隔|Δx|无限变小时,点P无限趋近于点P0,于是割线PP0无限趋近于点P0处的切线P0T,这时,割线PP0的斜率k无限趋近于点P0处的切线P0T的斜率k0.
注意点:极限的几何意义:曲线y=f(x)在x=x0处的切线斜率.
例3 求抛物线f(x)=x2-2x+3在点(1,2)处的切线方程.
所以切线的方程为y-2=0×(x-1),即y=2.
延伸探究 本例函数不变,求与2x-y+4=0平行的该曲线的切线方程.
=2x0-2+Δx,
故有2x0-2=2,解得x0=2,
所以切点为(2,3),所求切线方程为2x-y-1=0.
反思感悟 (1)求抛物线在某点处的切线方程的步骤
(2)求曲线过某点的切线方程需注意,该点不一定是切点,需另设切点坐标.
跟踪训练3 求抛物线f(x)=x2-x在点(2,2)处的切线方程.
解 f(2+Δx)-f(2)=(2+Δx)2-(2+Δx)-2
=3Δx+(Δx)2,
则切线方程为y-2=3(x-2),即3x-y-4=0.
1.知识清单:
(1)平均速度.
(2)瞬时速度.
(3)曲线在某点处的切线方程.
2.方法归纳:极限法、定义法.
3.常见误区:对割线的斜率与切线的斜率之间的关系理解不到位.
课堂小结
随堂演练
1
2
3
4
1.某质点的运动方程为s(t)=1-t2,则该物体在[1,2]内的平均速度为
A.2 B.3 C.-2 D.-3
√
1
2
3
4
2.一个物体做直线运动,位移s与时间t之间的函数关系式为s(t)=t2+2t+3,则该物体在t=2时的瞬时速度为
A.4 B.5 C.6 D.7
√
1
2
3
4
3.一物体做直线运动,其运动方程为s(t)=-t2+2t,则t=0时,其速度为
A.-2 B.-1 C.0 D.2
所以当t=0时,其速度为2.
√
1
2
3
4
4.抛物线y=x2+4在点(1,5)处的切线的斜率为_____.
2
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
2.已知抛物线y=3x-x2在x0=2处的增量为Δx=0.1,则 的值为
A.-0.11 B.-1.1 C.3.89 D.0.29
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵Δy=f(2+0.1)-f(2)=(3×2.1-2.12)-(3×2-22)=-0.11,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知函数f(x)=2x2-4的图象上两点A,B,且xA=1,xB=1.1,则函数f(x)从A点到B点的平均变化率为
A.4 B.4x C.4.2 D.4.02
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 由瞬时速度与平均速度的关系可知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
5.已知曲线y=2x2上一点A(2,8),则在点A处的切线斜率为
A.4 B.16 C.8 D.2
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知某物体的运动方程为s(t)=7t2+8(0≤t≤5),则
A.该物体在1≤t≤3时的平均速度是28
B.该物体在t=4时的瞬时速度是56
C.该物体位移的最大值为43
D.该物体在t=5时的瞬时速度是70
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 该物体在1≤t≤3时的平均速度是
物体的最大位移是7×52+8=183,C错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.一做直线运动的物体,其位移s与时间t的关系是s=3t-t2,则物体的初速度是_____.
3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.若抛物线f(x)=4x2在点(x0,f(x0))处切线的斜率为8,则x0=_____.
1
解得x0=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.某物体按照s(t)=3t2+2t+4(s的单位:m)的规律做直线运动,求自运动开始到4 s时物体运动的平均速度和4 s时的瞬时速度.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 自运动开始到t s时,物体运动的平均速度
由于Δs=3(t+Δt)2+2(t+Δt)+4-(3t2+2t+4)
=(2+6t)Δt+3(Δt)2.
所以4 s时物体的瞬时速度为26 m/s.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.曲线f(x)=x2上哪一点处的切线满足下列条件?
(1)平行于直线y=4x-5;
解 设P(x0,y0)是满足条件的点,曲线f(x)=x2在点P(x0,y0)处切线的斜率为
∵切线与直线y=4x-5平行,∴2x0=4,x0=2,
y0=4,即P(2,4)是满足条件的点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)垂直于直线2x-6y+5=0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)倾斜角为135°.
解 因为切线的倾斜角为135°,
所以其斜率为-1,即2x0=-1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设直线O′A,AB,BC的斜率分别为kO′A,kAB,kBC,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则
A.a=1,b=1 B.a=-1,b=1
C.a=1,b=-1 D.a=-1,b=-1
√
解析 由题意可知
解得a=1,又(0,b)在切线上,∴b=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.A,B两机关开展节能活动,活动开始后两机关的用电量W1(t),W2(t)与时间t(天)的关系如图所示,则一定有
A.两机关节能效果一样好
B.A机关比B机关节能效果好
C.A机关的用电量在[0,t0]上的平均变化率比B机关的用电量在[0,t0]上
的平均变化率大
D.A机关与B机关自节能以来用电量总是一样大
√
解析 由题图可知,A,B两机关用电量在[0,t0]上的平均变化率都小于0,由平均变化率的几何意义知,A机关用电量在[0,t0]上的平均变化率小于B机关的平均变化率,从而A机关比B机关节能效果好.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.函数f(x)=x2-x在区间[-2,t]上的平均变化率是2,则t=_____.
5
解析 因为函数f(x)=x2-x在区间[-2,t]上的平均变化率是2,
即t2-t-6=2t+4,
从而t2-3t-10=0,
解得t=5或t=-2(舍去).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.将半径为R的球加热,若半径从R=1到R=m时球的体积膨胀率为 ,则m的值为_____.
2
所以m2+m+1=7,所以m=2或m=-3(舍).
16.若一物体运动方程如下:(位移单位:m,时间单位:s)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
求:(1)物体在t∈[3,5]内的平均速度;
解 ∵物体在t∈[3,5]上的时间变化量为Δt=5-3=2,
物体在t∈[3,5]上的位移变化量为
Δs=3×52+2-(3×32+2)=3×(52-32)=48,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴物体在t∈[3,5]上的平均速度为24 m/s.
(2)物体的初速度v0;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 求物体的初速度v0,即求物体在t=0时的瞬时速度.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)物体在t=1时的瞬时速度.
∴物体在t=1时的瞬时速度为
