第五章 5.3.1函数的单调性 课件(共70张PPT)
文档属性
| 名称 | 第五章 5.3.1函数的单调性 课件(共70张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 07:31:22 | ||
图片预览











文档简介
(共70张PPT)
5.3.1 函数的单调性
第五章 §5.3 导数在研究函数中的应用
1.结合实例,借助几何直观了解函数的单调性与导数的关系.
2.能利用导数研究函数的单调性.
3.对于多项式函数,能求不超过三次的多项式函数的单调区间.
学习目标
同学们,对于函数的单调性,大家并不陌生,早在学习必修第一册的时候,我们就利用定义法和图象法求了函数的单调区间,比如大家所熟悉的一次函数、二次函数等.当然,求单调区间的前提是要先确定函数的定义域,但是对于更复杂一些的函数,比如三次函数、与指数或对数有关的函数等,虽然定义法是解决问题的根本方法,但定义法比较烦琐,又不能画出函数图象,为了解决这个问题,就需要用到我们今天的知识:函数的单调性与导数的关系.
导语
随堂演练
课时对点练
一、函数的单调性与导数的关系
二、利用导数求函数的单调区间
三、由导数的信息画函数的大致图象
内容索引
一、函数的单调性与导数的关系
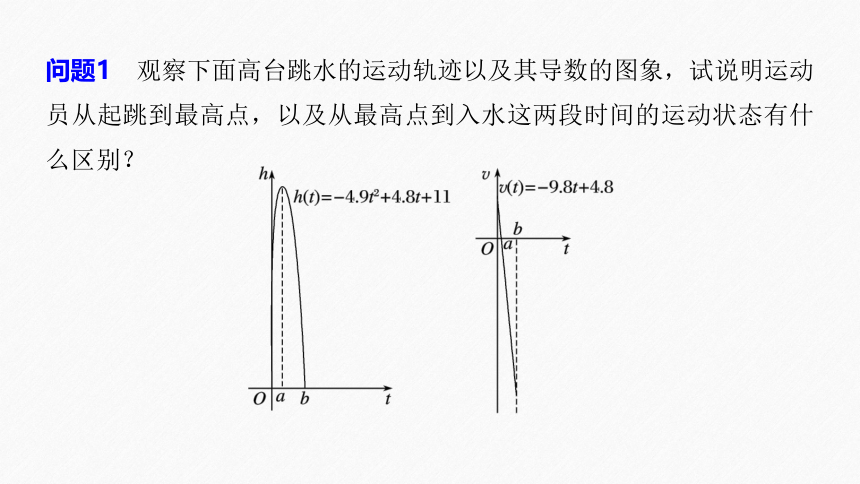
问题1 观察下面高台跳水的运动轨迹以及其导数的图象,试说明运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
提示 通过观察图象,可以发现
(1)运动员从起点到最高点,离水面的高度h随时间t的增加而增加,即h(t)单调递增,相应地,v(t)=h′(t)>0;
(2)从最高点到入水,离水面的高度h随时间t的增加而减小,即h(t)单调递减,相应地,v(t)=h′(t)<0.
问题2 观察下面几个图象,探究函数的单调性和导数的正负的关系.
提示 (1)函数y=x的定义域为R,并且在定义域上是增函数,其导数y′=1>0;
(2)函数y=x2的定义域为R,在(-∞,0)上单调递减,在(0,+∞)上单调递增.而y′=2x,当x<0时,其导数y′<0;当x>0时,其导数y′>0;当x=0时,其导数y′=0.
(3)函数y=x3的定义域为R,在定义域上为增函数.而y′=3x2,当x≠0时,其导数3x2>0;当x=0时,其导数3x2=0;
从以上四个函数的单调性及其导数符号的关系上说明,在区间(a,b)内,如果f′(x)>0,那么函数y=f(x)在这个区间上单调递增;如果f′(x)<0,那么函数y=f(x)在这个区间上单调递减.
知识梳理
函数的单调性与其导数的正负之间的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 单调递___
f′(x)<0 单调递___
增
减
注意点:(1)当f′(x)=0时,f(x)是常函数;(2)原函数的图象只看增(减)的变化,导函数的图象只看正(负)变化.
例1 利用导数判断下列函数的单调性:
所以f′(x)=x2-2x+2=(x-1)2+1>0,
(3)f(x)=x-ex(x>0).
解 因为f(x)=x-ex,x∈(0,+∞),
所以f′(x)=1-ex<0,
所以f(x)=x-ex在(0,+∞)上单调递减.
反思感悟 利用导数判断函数单调性的步骤:确定函数的定义域;求导数f′(x);确定f′(x)在定义域内的符号,在此过程中,需要对导函数进行通分、因式分解等变形;得出结论.
解 因为f(x)=x2-2x+aln x,x∈(0,+∞),
所以f(x)=x2-2x+aln x在x∈(0,+∞)上单调递增.
二、利用导数求函数的单调区间
例2 求下列函数的单调区间.
(1)f(x)=3x2-2ln x;
解 易知函数的定义域为(0,+∞).
用x1分割定义域,得下表:
(2)f(x)=2x3+3x2-36x+1.
解 f′(x)=6x2+6x-36.
由f′(x)>0得6x2+6x-36>0,解得x<-3或x>2;
由f′(x)<0得6x2+6x-36<0,解得 -3故f(x)的单调递增区间是(-∞,-3),(2,+∞);
单调递减区间是(-3,2).
反思感悟 利用导数判断函数的单调性的一般步骤
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.
或(1)确定函数y=f(x)的定义域.
(2)求导数y=f′(x).
(3)解不等式f′(x)>0,函数在解集与定义域的交集上单调递增.
(4)解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.
跟踪训练2 求下列函数的单调区间.
(1)f(x)=x2·e-x;
解 易知函数的定义域为(-∞,+∞).
f′(x)=(x2)′e-x+x2(e-x)′=2xe-x-x2e-x=e-x·(2x-x2),
令f′(x)=0,得x=0或x=2,
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 f(0) 单调递增 f(2) 单调递减
∴f(x)的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2).
解 易知函数的定义域为(-∞,0)∪(0,+∞).
∴函数f(x)的单调递减区间为(-1,0)和(0,1),
单调递增区间为(-∞,-1)和(1,+∞).
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,0) (0,1) 1 (1,+∞)
f′(x) + 0 - - 0 +
f(x) 单调 递增 f(-1) 单调 递减 单调 递减 f(1) 单调
递增
三、由导数的信息画函数的大致图象
例3 已知导函数f′(x)的下列信息:当x<0或x>7时,f′(x)>0;当0解 当x<0或x>7时,f′(x)>0,可知函数f(x)在区间(-∞,0)和(7,+∞)上都是单调递增的;
当0当x=0或x=7时,f′(x)=0,
这两个点比较特殊,我们称它们为“临界点”.
故如图,
反思感悟 由导函数图象画原函数图象的依据:根据f′(x)>0,则f(x)单调递增,f′(x)<0,则f(x)单调递减;
由原函数图象画导函数图象的依据:若f(x)单调递增,则f′(x)的图象一定在x轴的上方;若f(x)单调递减,则f′(x)的图象一定在x轴的下方;若f(x)是常函数,则f′(x)=0.
跟踪训练3 (1)已知f(x)的导函数f′(x)的图象如图所示,那么f(x)的图象最有可能是图中的
√
解析 由题意可知,当x<0和x>2时,导函数f′(x)<0,函数f(x)单调递减;
当x∈(0,2)时,导函数f′(x)>0,
函数f(x)单调递增,故函数f(x)的图象如图D.
(2)若函数y=f′(x)图象如图所示,则y=f(x)图象可能是
√
解析 由y=f′(x)图象可得:在(-∞,b)上f′(x)≥0,在(b,+∞)上f′(x)<0,
根据原函数图象与导函数图象的关系可得:y=f(x)在(-∞,b)上单调递增,在(b,+∞)上单调递减,可排除A,D,
且在x=0处,f′(x)=0,即在x=0处,y=f(x)的切线的斜率为0,可排除B,故选C.
1.知识清单:
(1)函数的单调性与其导数的关系.
(2)利用导数判断函数的单调性.
(3)利用导数求函数的单调区间.
(4)由导数的信息画函数的大致图象.
2.方法归纳:方程思想、分类讨论.
3.常见误区:忽略定义域的限制.
课堂小结
随堂演练
1
2
3
4
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
1
2
3
4
解析 ∵f(x)在(-∞,1),(4,+∞)上单调递减,
在(1,4)上单调递增,
∴当x<1或x>4时,f′(x)<0;
当1<x<4时,f′(x)>0.
1
2
3
4
2.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是
A.(-∞,2) B.(0,3)
C.(3,4) D.(2,+∞)
√
解析 ∵f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,∴x>2.
∴f(x)的单调递增区间为(2,+∞),CD符合.
√
1
2
3
4
√
解析 f′(x)=ln x+1(x>0),令f′(x)>0,
1
2
3
4
4.函数f(x)=x+2cos x,x∈(0,π)的单调递减区间是________.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(2,+∞)
C.(-∞,-1)∪(1,+∞)
D.(-2,-1)∪(1,2)
√
解析 因为f(x)在(-∞,-1),(1,+∞)上单调递增,
所以在区间(-∞,-1)和(1,+∞)上f′(x)>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)如图是函数y=f(x)的导函数f′(x)的图象,则下列判断正确的是
A.在区间(-2,1)上,f(x)单调递增
B.在(1,2)上,f(x)单调递增
C.在(4,5)上,f(x)单调递增
D.在(-3,-2)上,f(x)单调递增
√
√
解析 由题图知当x∈(1,2),x∈(4,5)时,f′(x)>0,
所以在(1,2),(4,5)上,f(x)单调递增,
当x∈(-3,-2)时,f′(x)<0,
所以在(-3,-2)上,f(x)单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x3-3x2+1的单调递减区间为
A.(2,+∞) B.(-∞,2)
C.(-∞,0) D.(0,2)
解析 f′(x)=3x2-6x=3x(x-2),
令f′(x)<0,得0所以f(x)的单调递减区间为(0,2).
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则该函数的图象可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由y=f′(x)的图象知,y=f(x)为增函数,且在区间(-1,0)上增长速度越来越快,而在区间(0,1)上增长速度越来越慢,故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题中图象可知,f(x)的大致图象如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.函数f(x)=(x2+x+1)ex的单调递减区间为____________.
(-2,-1)
解析 f′(x)=(2x+1)ex+(x2+x+1)ex=ex(x2+3x+2)=ex(x+1)(x+2),
令f′(x)<0,解得-2所以函数f(x)的单调递减区间为(-2,-1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.函数f(x)的图象如图所示,f′(x)为函数f(x)的导函数,则不等式
<0的解集为_________________.
(-3,-1)∪(0,1)
解析 由题图知,当x∈(-∞,-3)∪(-1,1)时,
f′(x)<0;
当x∈(-3,-1)∪(1,+∞)时,f′(x)>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.判断函数f(x)=2x(ex-1)-x2的单调性.
解 函数f(x)的定义域为R,f′(x)=2(ex-1+xex-x)=2(ex-1)(x+1).
当x∈(-∞,-1)时,f′(x)>0;
当x∈(-1,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
故f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)= 的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
(1)求函数y=f(x)的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 因为f(x)的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
由①②得a=2,b=3.
(因为b+1≠0,所以b=-1舍去)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.函数f(x)=xcos x的导函数f′(x)在区间[-π,π]上的图象大致是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)=xcos x,
所以f′(x)=cos x-xsin x.
因为f′(-x)=f′(x),
所以f′(x)为偶函数,
所以函数图象关于y轴对称.
由f′(0)=1可排除C,D.
而f′(1)=cos 1-sin 1<0,排除B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知定义域为R的函数f(x)的导函数的图象如图,则关于以下函数值的大小关系,一定正确的是
A.f(a)>f(b)>f(0) B.f(0)<f(c)<f(d)
C.f(b)<f(0)<f(c) D.f(c)<f(d)<f(e)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由f(x)的导函数图象可知,f(x)在(a,b),(c,e)上单调递增,在(b,c)上单调递减,所以f(a)f(b)>f(0)>f(c),B,C错误;
f(c)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.若定义在R上的函数y=f(x)满足f′(x)>f(x),则当a>0时,f(a)与eaf(0)的大小关系为
A.f(a)eaf(0)
C.f(a)=eaf(0) D.不能确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即f(a)>eaf(0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知函数f(x)是R上的偶函数,且在(0,+∞)上有f′(x)>0,若f(-1)=0,则关于x的不等式xf(x)<0的解集是__________________.
(-∞,-1)∪(0,1)
解析 因为在(0,+∞)上f′(x)>0,
所以f(x)在(0,+∞)上单调递增,
又f(x)为偶函数,
所以f(-1)=f(1)=0,
且f(x)在(-∞,0)上单调递减,
f(x)的草图如图所示,
所以xf(x)<0的解集为(-∞,-1)∪(0,1).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(多选)若函数exf(x)(e=2.718 28…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是
A.f(x)=2-x B.f(x)=x2+2
C.f(x)=3-x D.f(x)=cos x
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设g(x)=ex·f(x),
对于B,g(x)=(x2+2)ex,g′(x)=(x2+2x+2)ex=[(x+1)2+1]ex>0,
所以g(x)在定义域R上是增函数,故B正确;
对于D,g(x)=ex·cos x,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵曲线y=f(x)在点(1,f(1))处的切线与x轴平行,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可知h(x)在(0,+∞)上为减函数,
由h(1)=0知,当0h(1)=0,故f′(x)>0;
当x>1时,h(x)综上,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).
5.3.1 函数的单调性
第五章 §5.3 导数在研究函数中的应用
1.结合实例,借助几何直观了解函数的单调性与导数的关系.
2.能利用导数研究函数的单调性.
3.对于多项式函数,能求不超过三次的多项式函数的单调区间.
学习目标
同学们,对于函数的单调性,大家并不陌生,早在学习必修第一册的时候,我们就利用定义法和图象法求了函数的单调区间,比如大家所熟悉的一次函数、二次函数等.当然,求单调区间的前提是要先确定函数的定义域,但是对于更复杂一些的函数,比如三次函数、与指数或对数有关的函数等,虽然定义法是解决问题的根本方法,但定义法比较烦琐,又不能画出函数图象,为了解决这个问题,就需要用到我们今天的知识:函数的单调性与导数的关系.
导语
随堂演练
课时对点练
一、函数的单调性与导数的关系
二、利用导数求函数的单调区间
三、由导数的信息画函数的大致图象
内容索引
一、函数的单调性与导数的关系
问题1 观察下面高台跳水的运动轨迹以及其导数的图象,试说明运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
提示 通过观察图象,可以发现
(1)运动员从起点到最高点,离水面的高度h随时间t的增加而增加,即h(t)单调递增,相应地,v(t)=h′(t)>0;
(2)从最高点到入水,离水面的高度h随时间t的增加而减小,即h(t)单调递减,相应地,v(t)=h′(t)<0.
问题2 观察下面几个图象,探究函数的单调性和导数的正负的关系.
提示 (1)函数y=x的定义域为R,并且在定义域上是增函数,其导数y′=1>0;
(2)函数y=x2的定义域为R,在(-∞,0)上单调递减,在(0,+∞)上单调递增.而y′=2x,当x<0时,其导数y′<0;当x>0时,其导数y′>0;当x=0时,其导数y′=0.
(3)函数y=x3的定义域为R,在定义域上为增函数.而y′=3x2,当x≠0时,其导数3x2>0;当x=0时,其导数3x2=0;
从以上四个函数的单调性及其导数符号的关系上说明,在区间(a,b)内,如果f′(x)>0,那么函数y=f(x)在这个区间上单调递增;如果f′(x)<0,那么函数y=f(x)在这个区间上单调递减.
知识梳理
函数的单调性与其导数的正负之间的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负 f(x)的单调性
f′(x)>0 单调递___
f′(x)<0 单调递___
增
减
注意点:(1)当f′(x)=0时,f(x)是常函数;(2)原函数的图象只看增(减)的变化,导函数的图象只看正(负)变化.
例1 利用导数判断下列函数的单调性:
所以f′(x)=x2-2x+2=(x-1)2+1>0,
(3)f(x)=x-ex(x>0).
解 因为f(x)=x-ex,x∈(0,+∞),
所以f′(x)=1-ex<0,
所以f(x)=x-ex在(0,+∞)上单调递减.
反思感悟 利用导数判断函数单调性的步骤:确定函数的定义域;求导数f′(x);确定f′(x)在定义域内的符号,在此过程中,需要对导函数进行通分、因式分解等变形;得出结论.
解 因为f(x)=x2-2x+aln x,x∈(0,+∞),
所以f(x)=x2-2x+aln x在x∈(0,+∞)上单调递增.
二、利用导数求函数的单调区间
例2 求下列函数的单调区间.
(1)f(x)=3x2-2ln x;
解 易知函数的定义域为(0,+∞).
用x1分割定义域,得下表:
(2)f(x)=2x3+3x2-36x+1.
解 f′(x)=6x2+6x-36.
由f′(x)>0得6x2+6x-36>0,解得x<-3或x>2;
由f′(x)<0得6x2+6x-36<0,解得 -3
单调递减区间是(-3,2).
反思感悟 利用导数判断函数的单调性的一般步骤
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.
或(1)确定函数y=f(x)的定义域.
(2)求导数y=f′(x).
(3)解不等式f′(x)>0,函数在解集与定义域的交集上单调递增.
(4)解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.
跟踪训练2 求下列函数的单调区间.
(1)f(x)=x2·e-x;
解 易知函数的定义域为(-∞,+∞).
f′(x)=(x2)′e-x+x2(e-x)′=2xe-x-x2e-x=e-x·(2x-x2),
令f′(x)=0,得x=0或x=2,
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 f(0) 单调递增 f(2) 单调递减
∴f(x)的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2).
解 易知函数的定义域为(-∞,0)∪(0,+∞).
∴函数f(x)的单调递减区间为(-1,0)和(0,1),
单调递增区间为(-∞,-1)和(1,+∞).
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-1) -1 (-1,0) (0,1) 1 (1,+∞)
f′(x) + 0 - - 0 +
f(x) 单调 递增 f(-1) 单调 递减 单调 递减 f(1) 单调
递增
三、由导数的信息画函数的大致图象
例3 已知导函数f′(x)的下列信息:当x<0或x>7时,f′(x)>0;当0
当0
这两个点比较特殊,我们称它们为“临界点”.
故如图,
反思感悟 由导函数图象画原函数图象的依据:根据f′(x)>0,则f(x)单调递增,f′(x)<0,则f(x)单调递减;
由原函数图象画导函数图象的依据:若f(x)单调递增,则f′(x)的图象一定在x轴的上方;若f(x)单调递减,则f′(x)的图象一定在x轴的下方;若f(x)是常函数,则f′(x)=0.
跟踪训练3 (1)已知f(x)的导函数f′(x)的图象如图所示,那么f(x)的图象最有可能是图中的
√
解析 由题意可知,当x<0和x>2时,导函数f′(x)<0,函数f(x)单调递减;
当x∈(0,2)时,导函数f′(x)>0,
函数f(x)单调递增,故函数f(x)的图象如图D.
(2)若函数y=f′(x)图象如图所示,则y=f(x)图象可能是
√
解析 由y=f′(x)图象可得:在(-∞,b)上f′(x)≥0,在(b,+∞)上f′(x)<0,
根据原函数图象与导函数图象的关系可得:y=f(x)在(-∞,b)上单调递增,在(b,+∞)上单调递减,可排除A,D,
且在x=0处,f′(x)=0,即在x=0处,y=f(x)的切线的斜率为0,可排除B,故选C.
1.知识清单:
(1)函数的单调性与其导数的关系.
(2)利用导数判断函数的单调性.
(3)利用导数求函数的单调区间.
(4)由导数的信息画函数的大致图象.
2.方法归纳:方程思想、分类讨论.
3.常见误区:忽略定义域的限制.
课堂小结
随堂演练
1
2
3
4
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为
√
1
2
3
4
解析 ∵f(x)在(-∞,1),(4,+∞)上单调递减,
在(1,4)上单调递增,
∴当x<1或x>4时,f′(x)<0;
当1<x<4时,f′(x)>0.
1
2
3
4
2.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是
A.(-∞,2) B.(0,3)
C.(3,4) D.(2,+∞)
√
解析 ∵f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,∴x>2.
∴f(x)的单调递增区间为(2,+∞),CD符合.
√
1
2
3
4
√
解析 f′(x)=ln x+1(x>0),令f′(x)>0,
1
2
3
4
4.函数f(x)=x+2cos x,x∈(0,π)的单调递减区间是________.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f′(x)>0的解集为
A.(-2,0)∪(2,+∞)
B.(-∞,-2)∪(2,+∞)
C.(-∞,-1)∪(1,+∞)
D.(-2,-1)∪(1,2)
√
解析 因为f(x)在(-∞,-1),(1,+∞)上单调递增,
所以在区间(-∞,-1)和(1,+∞)上f′(x)>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.(多选)如图是函数y=f(x)的导函数f′(x)的图象,则下列判断正确的是
A.在区间(-2,1)上,f(x)单调递增
B.在(1,2)上,f(x)单调递增
C.在(4,5)上,f(x)单调递增
D.在(-3,-2)上,f(x)单调递增
√
√
解析 由题图知当x∈(1,2),x∈(4,5)时,f′(x)>0,
所以在(1,2),(4,5)上,f(x)单调递增,
当x∈(-3,-2)时,f′(x)<0,
所以在(-3,-2)上,f(x)单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x3-3x2+1的单调递减区间为
A.(2,+∞) B.(-∞,2)
C.(-∞,0) D.(0,2)
解析 f′(x)=3x2-6x=3x(x-2),
令f′(x)<0,得0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则该函数的图象可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由y=f′(x)的图象知,y=f(x)为增函数,且在区间(-1,0)上增长速度越来越快,而在区间(0,1)上增长速度越来越慢,故选B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题中图象可知,f(x)的大致图象如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.函数f(x)=(x2+x+1)ex的单调递减区间为____________.
(-2,-1)
解析 f′(x)=(2x+1)ex+(x2+x+1)ex=ex(x2+3x+2)=ex(x+1)(x+2),
令f′(x)<0,解得-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.函数f(x)的图象如图所示,f′(x)为函数f(x)的导函数,则不等式
<0的解集为_________________.
(-3,-1)∪(0,1)
解析 由题图知,当x∈(-∞,-3)∪(-1,1)时,
f′(x)<0;
当x∈(-3,-1)∪(1,+∞)时,f′(x)>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.判断函数f(x)=2x(ex-1)-x2的单调性.
解 函数f(x)的定义域为R,f′(x)=2(ex-1+xex-x)=2(ex-1)(x+1).
当x∈(-∞,-1)时,f′(x)>0;
当x∈(-1,0)时,f′(x)<0;
当x∈(0,+∞)时,f′(x)>0.
故f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)= 的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
(1)求函数y=f(x)的解析式;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 因为f(x)的图象在点M(-1,f(-1))处的切线方程为x+2y+5=0.
由①②得a=2,b=3.
(因为b+1≠0,所以b=-1舍去)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.函数f(x)=xcos x的导函数f′(x)在区间[-π,π]上的图象大致是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)=xcos x,
所以f′(x)=cos x-xsin x.
因为f′(-x)=f′(x),
所以f′(x)为偶函数,
所以函数图象关于y轴对称.
由f′(0)=1可排除C,D.
而f′(1)=cos 1-sin 1<0,排除B.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知定义域为R的函数f(x)的导函数的图象如图,则关于以下函数值的大小关系,一定正确的是
A.f(a)>f(b)>f(0) B.f(0)<f(c)<f(d)
C.f(b)<f(0)<f(c) D.f(c)<f(d)<f(e)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由f(x)的导函数图象可知,f(x)在(a,b),(c,e)上单调递增,在(b,c)上单调递减,所以f(a)
f(c)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.若定义在R上的函数y=f(x)满足f′(x)>f(x),则当a>0时,f(a)与eaf(0)的大小关系为
A.f(a)
C.f(a)=eaf(0) D.不能确定
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即f(a)>eaf(0).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知函数f(x)是R上的偶函数,且在(0,+∞)上有f′(x)>0,若f(-1)=0,则关于x的不等式xf(x)<0的解集是__________________.
(-∞,-1)∪(0,1)
解析 因为在(0,+∞)上f′(x)>0,
所以f(x)在(0,+∞)上单调递增,
又f(x)为偶函数,
所以f(-1)=f(1)=0,
且f(x)在(-∞,0)上单调递减,
f(x)的草图如图所示,
所以xf(x)<0的解集为(-∞,-1)∪(0,1).
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.(多选)若函数exf(x)(e=2.718 28…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是
A.f(x)=2-x B.f(x)=x2+2
C.f(x)=3-x D.f(x)=cos x
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设g(x)=ex·f(x),
对于B,g(x)=(x2+2)ex,g′(x)=(x2+2x+2)ex=[(x+1)2+1]ex>0,
所以g(x)在定义域R上是增函数,故B正确;
对于D,g(x)=ex·cos x,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵曲线y=f(x)在点(1,f(1))处的切线与x轴平行,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
可知h(x)在(0,+∞)上为减函数,
由h(1)=0知,当0
当x>1时,h(x)
