第五章 5.3.2 第1课时 函数的极值 课件(共77张PPT)
文档属性
| 名称 | 第五章 5.3.2 第1课时 函数的极值 课件(共77张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 07:31:55 | ||
图片预览








文档简介
(共77张PPT)
第1课时 函数的极值
第五章 5.3.2 函数的极值与最大(小)值
1.了解函数极值的概念,会从几何方面直观理解函数的极值与导
数的关系.
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
学习目标
同学们,前面我们通过对函数的求导,摸清了函数的单调性,从而也发现了函数图象的变化趋势,正所谓“横看成岭侧成峰,远近高低各不同”,大家可以展开想象一下,在群山之中,各个山峰的顶端虽然不一定是群山之中的最高处,但却是其附近的最高点,同样,各个谷底虽然不一定是山谷的最低处,但却是其附近的最低点.这就是我们今天要研究的函数的极值.
导语
随堂演练
课时对点练
一、函数极值概念的理解
二、求函数的极值
三、由极值求参数的值或范围
内容索引
一、函数极值概念的理解
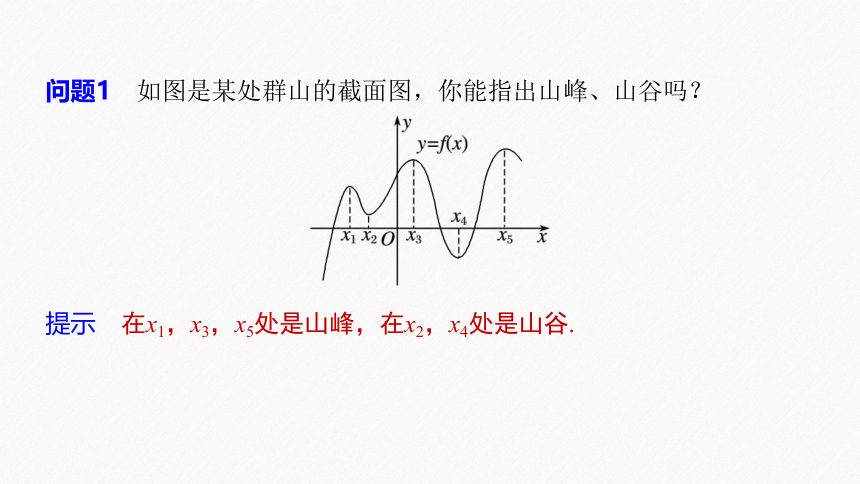
问题1 如图是某处群山的截面图,你能指出山峰、山谷吗?
提示 在x1,x3,x5处是山峰,在x2,x4处是山谷.
问题2 你能描述一下在各个山峰、山谷附近的特点吗?
提示 以山峰x=x1处为例来研究,在x=x1处,它附近的函数值都比它小,且在x=x1处的左侧函数是单调递增的,且有f′(x)>0,在x=x1处的右侧函数是单调递减的,且有f′(x)<0,函数图象是连续不断的,f′(x)的变化也是连续不断的,并且有f′(x1)=0.
知识梳理
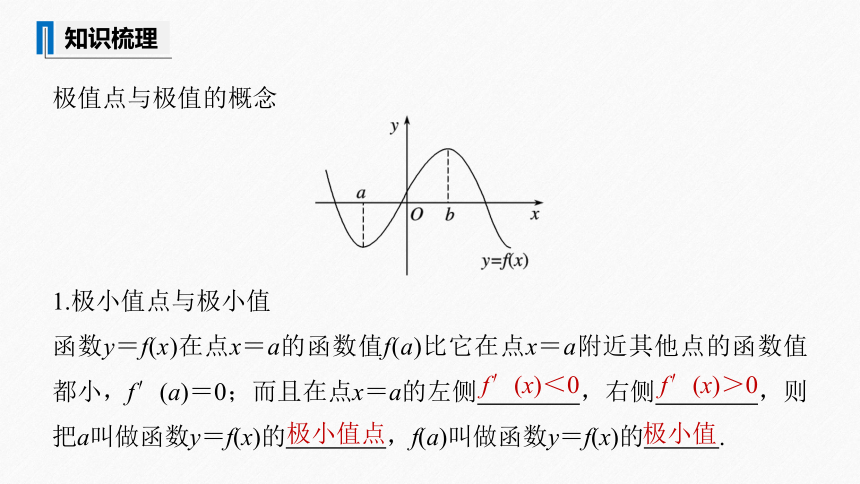
极值点与极值的概念
1.极小值点与极小值
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a的左侧 ,右侧 ,则把a叫做函数y=f(x)的 ,f(a)叫做函数y=f(x)的 .
f′(x)<0
f′(x)>0
极小值点
极小值
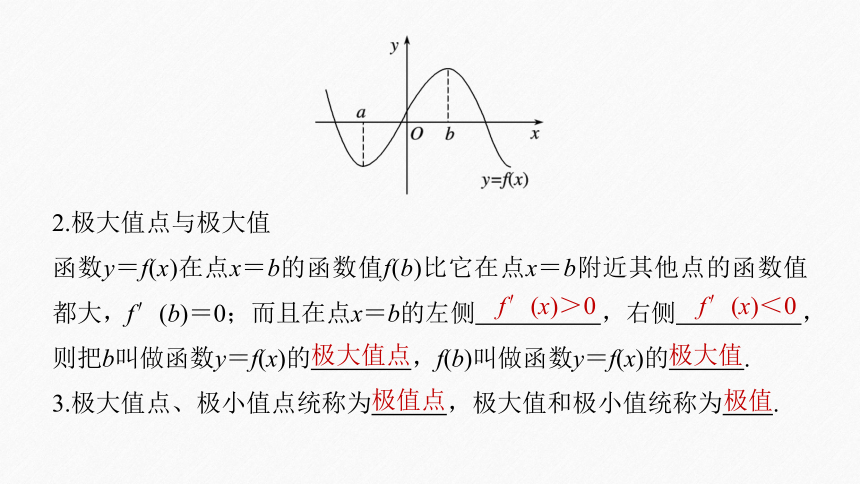
2.极大值点与极大值
函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b的左侧 ,右侧 ,则把b叫做函数y=f(x)的 ,f(b)叫做函数y=f(x)的 .
3.极大值点、极小值点统称为 ,极大值和极小值统称为 .
f′(x)>0
f′(x)<0
极大值点
极大值
极值点
极值
注意点:(1)极值点不是点;(2)极值是函数的局部性质;(3)函数的极值不唯一;(4)极大值与极小值两者的大小不确定;(5)极值点出现在区间的内部,端点不能是极值点;(6)若f′(x0)=0,则x0不一定是极值点,即f′(x0)=0是f(x)在x=x0处取到极值的必要不充分条件,函数y=f′(x)的变号零点,才是函数的极值点.
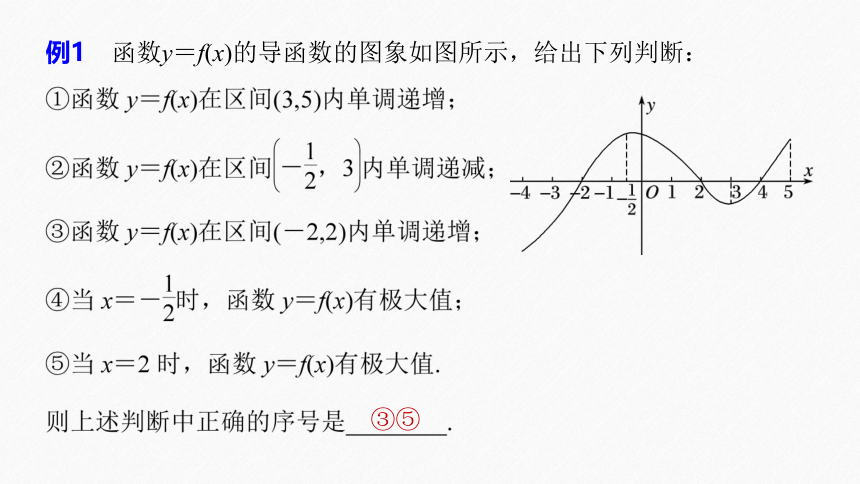
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
③⑤
解析 对于①,当x∈(3,4)时,f′(x)<0,f(x)单调递减,
当x∈(4,5)时,f′(x)>0,f(x)单调递增,所以①错误;
当x∈(2,3)时,f′(x)<0,f(x)单调递减,所以②错误;
对于③,当x∈(-2,2)时,f′(x)>0,f(x)单调递增,所以③正确;
对于④,当x∈(-2,2)时,f′(x)>0,f(x)单调递增,
对于⑤,由②知当x=2时,函数y=f(x)取得极大值,所以⑤正确.
反思感悟 解答此类问题要先搞清楚所给的图象是原函数还是导函数的,对于导函数的图象,重点考查在哪个区间上为正,哪个区间上为负,在哪个点处与x轴相交,在该点附近的导数值是如何变化的,若是由正值变为负值,则在该点处取得极大值;若是由负值变为正值,则在该点处取得极小值.
跟踪训练1 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)在区间(a,b)内的极小值点的个数为
A.1 B.2 C.3 D.4
√
解析 由图象,设f′(x)与x轴负半轴的两个交点的横坐标分别为c,d,
其中c所以此时函数f(x)在(-∞,c),(d,b)上单调递增,
在(c,d)上,f′(x)<0,此时f(x)在(c,d)上单调递减,
所以x=c时,函数取得极大值,x=d时,函数取得极小值.
则函数y=f(x)的极小值点的个数为1.
二、求函数的极值
例2 求下列函数的极值:
(1)f(x)=x3-3x2-9x+5;
解 函数f(x)的定义域为R.
f′(x)=3x2-6x-9,
令f′(x)=0,
即3x2-6x-9=0,
解得x1=-1,x2=3.
当x变化时,f(x),f′(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
∴当x=-1时,函数y=f(x)有极大值,
且f(-1)=10;
当x=3时,函数y=f(x)有极小值,且f(3)=-22.
(2)f(x)=x-aln x(a∈R).
解 f(x)=x-aln x的定义域为(0,+∞),
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,
解得x=a.
又当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
反思感悟 函数极值和极值点的求解步骤
(1)确定函数的定义域.
(2)求方程f′(x)=0的根.
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格.
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
跟踪训练2 求下列函数的极值:
(1)f(x)=x3-x;
解 函数f(x)的定义域为R.
当x变化时,f(x)和f′(x)变化情况如下表:
(2)f(x)=x2e-x.
解 函数f(x)的定义域为R,
f′(x)=2xe-x+x2·e-x·(-x)′=2xe-x-x2·e-x=x(2-x)e-x.
令f′(x)=0,得x(2-x)·e-x=0,解得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 0 单调递增 4e-2 单调递减
因此当x=0时,f(x)取得极小值,且极小值为f(0)=0;
当x=2时,f(x)取得极大值,
三、由极值求参数的值或范围
例3 (1)若函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则a=_____,b=_____.
4
-11
解析 f′(x)=3x2+2ax+b,
但由于当a=-3,b=3时,
f′(x)=3x2-6x+3=3(x-1)2≥0,
故f(x)在R上单调递增,不可能在x=1处取得极值,
不符合题意,应舍去.
而当a=4,b=-11时,经检验知符合题意,
故a,b的值分别为4,-11.
解 f′(x)=x2-(m+3)x+m+6.
因为函数f(x)在(1,+∞)内有两个极值点,
所以f′(x)=x2-(m+3)x+m+6在(1,+∞)内与x轴有两个不同的交点,如图所示.
解得m>3.
故实数m的取值范围是(3,+∞).
反思感悟 已知函数的极值求参数的方法
(1)对于已知可导函数的极值求参数的问题,解题的切入点是极值存在的条件:极值点处的导数值为0,极值点两侧的导数值异号.
注意:求出参数后,一定要验证是否满足题目的条件.
(2)对于函数无极值的问题,往往转化为其导函数的值非负或非正在某区间内恒成立的问题,即转化为f′(x)≥0或f′(x)≤0在某区间内恒成立的问题,此时需注意不等式中的等号是否成立.
跟踪训练3 若函数f(x)= x3-4x+4的图象与直线y=a恰有三个不同
的交点,则实数a的取值范围是__________.
∴f′(x)=x2-4=(x+2)(x-2).
令f′(x)=0,得x=2或x=-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
且f(x)在(-∞,-2)上单调递增,在(-2,2)上单调递减,在(2,+∞)上单调递增.
根据函数单调性、极值的情况,它的图象大致如图所示,
1.知识清单:
(1)函数极值的定义.
(2)函数极值的判定及求法.
(3)函数极值的应用.
2.方法归纳:方程思想、分类讨论.
3.常见误区:导数值等于零不是此点为极值点的充要条件.
课堂小结
随堂演练
1
2
3
4
1.函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论错误的是
A.在(1,2)上函数f(x)单调递增
B.在(3,4)上函数f(x)单调递减
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
√
1
2
3
4
解析 根据导函数图象知,x∈(1,2)时,f′(x)>0;
x∈(2,4)时,f′(x)<0,x∈(4,5)时,f′(x)>0.
∴f(x)在(1,2),(4,5)上单调递增,在(2,4)上单调递减,
x=2是f(x)在[1,5]上的极大值点,x=4是极小值点.
1
2
3
4
2.(多选)已知函数f(x)=2x3+ax2+36x-24在x=2处有极值,则该函数的一个单调递增区间是
A.(-∞,2) B.(3,+∞)
C.(2,+∞) D.(-∞,3)
√
解析 ∵f′(x)=6x2+2ax+36,且在x=2处有极值,
∴f′(2)=0,即24+4a+36=0,解得a=-15,
∴f′(x)=6x2-30x+36=6(x-2)(x-3),
由f′(x)>0得x<2或x>3.
√
1
2
3
4
3.设函数f(x)=xex,则
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=-1为f(x)的极大值点
D.x=-1为f(x)的极小值点
√
解析 令f′(x)=ex+x·ex=(1+x)ex=0,得x=-1.
当x<-1时,f′(x)<0;
当x>-1时,f′(x)>0.
故x=-1为f(x)的极小值点.
1
2
3
4
4.已知曲线f(x)=x3+ax2+bx+1在点(1,f(1))处的切线斜率为3,且x=
是y=f(x)的极值点,则a=_____,b=_______.
2
-4
解析 f′(x)=3x2+2ax+b,
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.下列函数中存在极值的是
A.y= B.y=x-ex
C.y=2 D.y=x3
解析 对于y=x-ex,y′=1-ex,
令y′=0,得x=0.
在区间(-∞,0)上,y′>0;
在区间(0,+∞)上,y′<0.
故当x=0时,函数y=x-ex取得极大值.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.设函数f(x)在R上可导,其导函数为f′(x),且函数y=f′(x)的图象如图所示,则下列结论中一定成立的是
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题图可知,当x<-2时,f′(x)>0;
当-2当1当x>2时,f′(x)>0.
由此可以得到函数f(x)在x=-2处取得极大值,
在x=2处取得极小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=ln x-x在区间(0,e)上的极大值为
A.-e B.-1
C.1-e D.0
令f′(x)=0,得x=1.
当x∈(0,1)时,f′(x)>0,
当x∈(1,e)时,f′(x)<0,
故f(x)在x=1处取得极大值f(1)=ln 1-1=0-1=-1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知a是函数f(x)=x3-12x的极小值点,则a等于
A.-4 B.-2 C.4 D.2
√
解析 ∵f(x)=x3-12x,
∴f′(x)=3x2-12,
令f′(x)=0,则x1=-2,x2=2.
当x∈(-∞,-2),(2,+∞)时,f′(x)>0,则f(x)单调递增;
当x∈(-2,2)时,f′(x)<0,则f(x)单调递减,
∴f(x)的极小值点为a=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数f(x)=x3+ax2+bx+a2+a在x=1处有极值为7,则a等于
A.-3或3 B.3或-9 C.3 D.-3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=3x2+2ax+b,
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-3当x>1时,f′(x)>0,x=1是极小值点;
当a=-3,b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,x=1不是极值点.
∴a=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的值可以是
A.-4 B.-3 C.6 D.8
√
√
解析 由题意知f′(x)=3x2+2ax+(a+6)=0有两个不相等的根,
所以Δ=4a2-12(a+6)>0,
解得a>6或a<-3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.函数f(x)= 的极小值为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f′(x)<0,得x<-2或x>1;
令f′(x)>0,得-2所以f(x)在(-∞,-2),(1,+∞)上单调递减,
在(-2,1)上单调递增,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点,则常数a=
_____.
经检验,符合题意.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设函数f(x)=aln x+ +1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
由题意知,曲线在x=1处的切线斜率为0,即f′(1)=0,
解得a=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的极值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当x∈(0,1)时,f′(x)<0,
故f(x)在(0,1)上单调递减;
当x∈(1,+∞)时,f′(x)>0,故f(x)在(1,+∞)上单调递增.
故f(x)在x=1处取得极小值,极小值为f(1)=3,无极大值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.设a为实数,函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=3x2-2x-1.
当x变化时,f′(x),f(x)的变化情况如下表:
极小值是f(1)=a-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当a在什么范围内取值时,曲线y=f(x)与x轴仅有一个交点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 函数f(x)=x3-x2-x+a
=(x-1)2(x+1)+a-1,
由此可知,x取足够大的正数时,有f(x)>0,
x取足够小的负数时,有f(x)<0,
∴曲线y=f(x)与x轴至少有一个交点.
f(x)极小值=f(1)=a-1.
∵曲线y=f(x)与x轴仅有一个交点,
∴f(x)极大值<0或f(x)极小值>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=-2处取得极小值,则函数y=xf′(x)的图象可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)在x=-2处取得极小值,
所以当x<-2时,
f(x)单调递减,
即f′(x)<0;
当x>-2时,f(x)单调递增,即f′(x)>0.
所以当x<-2时,y=xf′(x)>0;
当x=-2时,y=xf′(x)=0;
当-2<x<0时,y=xf′(x)<0;
当x=0时,y=xf′(x)=0;
当x>0时,y=xf′(x)>0.
结合选项中的图象知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若函数f(x)=ex-ax-b在R上有小于0的极值点,则实数a的取值范围是
A.(-1,0) B.(0,1)
C.(-∞,-1) D.(1,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意知f′(x)=ex-a.
当a≤0时,f′(x)>0恒成立,则f(x)在R上单调递增,不符合题意;
当a>0时,令f′(x)=0,解得x=ln a,
∴当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
可知x=ln a为f(x)的极值点,∴ln a<0,∴a∈(0,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f′(x)=2x2-5ax+3a2,
由题意可得f′(3)=2×9-15a+3a2=0,
整理得a2-5a+6=0,解得a=2或a=3.
当a=2时,f′(x)=2x2-10x+12=2(x-2)(x-3),
令f′(x)>0,得x<2或x>3;
令f′(x)<0,得2此时,函数y=f(x)在x=3处取得极小值,不符合题意;
当a=3时,f′(x)=2x2-15x+27=(x-3)(2x-9).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
此时,函数y=f(x)在x=3处取得极大值,符合题意.
综上所述,a=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为______.
[1,5)
解析 ∵f′(x)=3x2+2x-a,
函数f(x)在区间(-1,1)上恰有一个极值点,
即f′(x)=0在(-1,1)内恰有一个根.
∴1≤a<5.
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知函数f(x)=ax3+bx2+cx的图象如图所示,且f(x)在x=x0与x=2处取得极值,则f(1)+f(-1)的值一定
A.等于0 B.大于0
C.小于0 D.小于或等于0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=3ax2+2bx+c.
令f′(x)=0,则x0和2是该方程的根.
由题图知,f′(x)<0的解集为(x0,2),
∴3a>0,则b>0,
∵f(1)+f(-1)=2b,
∴f(1)+f(-1)>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
分以下两种情况讨论:
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2a) -2a (-2a,a-2) a-2 (a-2,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以f(x)在(-∞,-2a),(a-2,+∞)上单调递增,
在(-2a,a-2)上单调递减,函数f(x)在x=-2a处取得极大值f(-2a),
且f(-2a)=3ae-2a,
函数f(x)在x=a-2处取得极小值f(a-2),且f(a-2)=(4-3a)·ea-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,a-2) a-2 (a-2,-2a) -2a (-2a,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以f(x)在(-∞,a-2),(-2a,+∞)上单调递增,在(a-2,-2a)上单调递减,
函数f(x)在x=a-2处取得极大值f(a-2),
且f(a-2)=(4-3a)ea-2,
函数f(x)在x=-2a处取得极小值f(-2a),
且f(-2a)=3ae-2a.
第1课时 函数的极值
第五章 5.3.2 函数的极值与最大(小)值
1.了解函数极值的概念,会从几何方面直观理解函数的极值与导
数的关系.
2.掌握函数极值的判定及求法.
3.掌握函数在某一点取得极值的条件.
学习目标
同学们,前面我们通过对函数的求导,摸清了函数的单调性,从而也发现了函数图象的变化趋势,正所谓“横看成岭侧成峰,远近高低各不同”,大家可以展开想象一下,在群山之中,各个山峰的顶端虽然不一定是群山之中的最高处,但却是其附近的最高点,同样,各个谷底虽然不一定是山谷的最低处,但却是其附近的最低点.这就是我们今天要研究的函数的极值.
导语
随堂演练
课时对点练
一、函数极值概念的理解
二、求函数的极值
三、由极值求参数的值或范围
内容索引
一、函数极值概念的理解
问题1 如图是某处群山的截面图,你能指出山峰、山谷吗?
提示 在x1,x3,x5处是山峰,在x2,x4处是山谷.
问题2 你能描述一下在各个山峰、山谷附近的特点吗?
提示 以山峰x=x1处为例来研究,在x=x1处,它附近的函数值都比它小,且在x=x1处的左侧函数是单调递增的,且有f′(x)>0,在x=x1处的右侧函数是单调递减的,且有f′(x)<0,函数图象是连续不断的,f′(x)的变化也是连续不断的,并且有f′(x1)=0.
知识梳理
极值点与极值的概念
1.极小值点与极小值
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a的左侧 ,右侧 ,则把a叫做函数y=f(x)的 ,f(a)叫做函数y=f(x)的 .
f′(x)<0
f′(x)>0
极小值点
极小值
2.极大值点与极大值
函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b的左侧 ,右侧 ,则把b叫做函数y=f(x)的 ,f(b)叫做函数y=f(x)的 .
3.极大值点、极小值点统称为 ,极大值和极小值统称为 .
f′(x)>0
f′(x)<0
极大值点
极大值
极值点
极值
注意点:(1)极值点不是点;(2)极值是函数的局部性质;(3)函数的极值不唯一;(4)极大值与极小值两者的大小不确定;(5)极值点出现在区间的内部,端点不能是极值点;(6)若f′(x0)=0,则x0不一定是极值点,即f′(x0)=0是f(x)在x=x0处取到极值的必要不充分条件,函数y=f′(x)的变号零点,才是函数的极值点.
例1 函数y=f(x)的导函数的图象如图所示,给出下列判断:
③⑤
解析 对于①,当x∈(3,4)时,f′(x)<0,f(x)单调递减,
当x∈(4,5)时,f′(x)>0,f(x)单调递增,所以①错误;
当x∈(2,3)时,f′(x)<0,f(x)单调递减,所以②错误;
对于③,当x∈(-2,2)时,f′(x)>0,f(x)单调递增,所以③正确;
对于④,当x∈(-2,2)时,f′(x)>0,f(x)单调递增,
对于⑤,由②知当x=2时,函数y=f(x)取得极大值,所以⑤正确.
反思感悟 解答此类问题要先搞清楚所给的图象是原函数还是导函数的,对于导函数的图象,重点考查在哪个区间上为正,哪个区间上为负,在哪个点处与x轴相交,在该点附近的导数值是如何变化的,若是由正值变为负值,则在该点处取得极大值;若是由负值变为正值,则在该点处取得极小值.
跟踪训练1 已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)在区间(a,b)内的极小值点的个数为
A.1 B.2 C.3 D.4
√
解析 由图象,设f′(x)与x轴负半轴的两个交点的横坐标分别为c,d,
其中c
在(c,d)上,f′(x)<0,此时f(x)在(c,d)上单调递减,
所以x=c时,函数取得极大值,x=d时,函数取得极小值.
则函数y=f(x)的极小值点的个数为1.
二、求函数的极值
例2 求下列函数的极值:
(1)f(x)=x3-3x2-9x+5;
解 函数f(x)的定义域为R.
f′(x)=3x2-6x-9,
令f′(x)=0,
即3x2-6x-9=0,
解得x1=-1,x2=3.
当x变化时,f(x),f′(x)的变化情况如下表:
x (-∞,-1) -1 (-1,3) 3 (3,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
∴当x=-1时,函数y=f(x)有极大值,
且f(-1)=10;
当x=3时,函数y=f(x)有极小值,且f(3)=-22.
(2)f(x)=x-aln x(a∈R).
解 f(x)=x-aln x的定义域为(0,+∞),
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,
解得x=a.
又当x∈(0,a)时,f′(x)<0,
当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
反思感悟 函数极值和极值点的求解步骤
(1)确定函数的定义域.
(2)求方程f′(x)=0的根.
(3)用方程f′(x)=0的根顺次将函数的定义域分成若干个小开区间,并列成表格.
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况.
跟踪训练2 求下列函数的极值:
(1)f(x)=x3-x;
解 函数f(x)的定义域为R.
当x变化时,f(x)和f′(x)变化情况如下表:
(2)f(x)=x2e-x.
解 函数f(x)的定义域为R,
f′(x)=2xe-x+x2·e-x·(-x)′=2xe-x-x2·e-x=x(2-x)e-x.
令f′(x)=0,得x(2-x)·e-x=0,解得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,0) 0 (0,2) 2 (2,+∞)
f′(x) - 0 + 0 -
f(x) 单调递减 0 单调递增 4e-2 单调递减
因此当x=0时,f(x)取得极小值,且极小值为f(0)=0;
当x=2时,f(x)取得极大值,
三、由极值求参数的值或范围
例3 (1)若函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则a=_____,b=_____.
4
-11
解析 f′(x)=3x2+2ax+b,
但由于当a=-3,b=3时,
f′(x)=3x2-6x+3=3(x-1)2≥0,
故f(x)在R上单调递增,不可能在x=1处取得极值,
不符合题意,应舍去.
而当a=4,b=-11时,经检验知符合题意,
故a,b的值分别为4,-11.
解 f′(x)=x2-(m+3)x+m+6.
因为函数f(x)在(1,+∞)内有两个极值点,
所以f′(x)=x2-(m+3)x+m+6在(1,+∞)内与x轴有两个不同的交点,如图所示.
解得m>3.
故实数m的取值范围是(3,+∞).
反思感悟 已知函数的极值求参数的方法
(1)对于已知可导函数的极值求参数的问题,解题的切入点是极值存在的条件:极值点处的导数值为0,极值点两侧的导数值异号.
注意:求出参数后,一定要验证是否满足题目的条件.
(2)对于函数无极值的问题,往往转化为其导函数的值非负或非正在某区间内恒成立的问题,即转化为f′(x)≥0或f′(x)≤0在某区间内恒成立的问题,此时需注意不等式中的等号是否成立.
跟踪训练3 若函数f(x)= x3-4x+4的图象与直线y=a恰有三个不同
的交点,则实数a的取值范围是__________.
∴f′(x)=x2-4=(x+2)(x-2).
令f′(x)=0,得x=2或x=-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
且f(x)在(-∞,-2)上单调递增,在(-2,2)上单调递减,在(2,+∞)上单调递增.
根据函数单调性、极值的情况,它的图象大致如图所示,
1.知识清单:
(1)函数极值的定义.
(2)函数极值的判定及求法.
(3)函数极值的应用.
2.方法归纳:方程思想、分类讨论.
3.常见误区:导数值等于零不是此点为极值点的充要条件.
课堂小结
随堂演练
1
2
3
4
1.函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论错误的是
A.在(1,2)上函数f(x)单调递增
B.在(3,4)上函数f(x)单调递减
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
√
1
2
3
4
解析 根据导函数图象知,x∈(1,2)时,f′(x)>0;
x∈(2,4)时,f′(x)<0,x∈(4,5)时,f′(x)>0.
∴f(x)在(1,2),(4,5)上单调递增,在(2,4)上单调递减,
x=2是f(x)在[1,5]上的极大值点,x=4是极小值点.
1
2
3
4
2.(多选)已知函数f(x)=2x3+ax2+36x-24在x=2处有极值,则该函数的一个单调递增区间是
A.(-∞,2) B.(3,+∞)
C.(2,+∞) D.(-∞,3)
√
解析 ∵f′(x)=6x2+2ax+36,且在x=2处有极值,
∴f′(2)=0,即24+4a+36=0,解得a=-15,
∴f′(x)=6x2-30x+36=6(x-2)(x-3),
由f′(x)>0得x<2或x>3.
√
1
2
3
4
3.设函数f(x)=xex,则
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=-1为f(x)的极大值点
D.x=-1为f(x)的极小值点
√
解析 令f′(x)=ex+x·ex=(1+x)ex=0,得x=-1.
当x<-1时,f′(x)<0;
当x>-1时,f′(x)>0.
故x=-1为f(x)的极小值点.
1
2
3
4
4.已知曲线f(x)=x3+ax2+bx+1在点(1,f(1))处的切线斜率为3,且x=
是y=f(x)的极值点,则a=_____,b=_______.
2
-4
解析 f′(x)=3x2+2ax+b,
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.下列函数中存在极值的是
A.y= B.y=x-ex
C.y=2 D.y=x3
解析 对于y=x-ex,y′=1-ex,
令y′=0,得x=0.
在区间(-∞,0)上,y′>0;
在区间(0,+∞)上,y′<0.
故当x=0时,函数y=x-ex取得极大值.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.设函数f(x)在R上可导,其导函数为f′(x),且函数y=f′(x)的图象如图所示,则下列结论中一定成立的是
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题图可知,当x<-2时,f′(x)>0;
当-2
由此可以得到函数f(x)在x=-2处取得极大值,
在x=2处取得极小值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=ln x-x在区间(0,e)上的极大值为
A.-e B.-1
C.1-e D.0
令f′(x)=0,得x=1.
当x∈(0,1)时,f′(x)>0,
当x∈(1,e)时,f′(x)<0,
故f(x)在x=1处取得极大值f(1)=ln 1-1=0-1=-1.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知a是函数f(x)=x3-12x的极小值点,则a等于
A.-4 B.-2 C.4 D.2
√
解析 ∵f(x)=x3-12x,
∴f′(x)=3x2-12,
令f′(x)=0,则x1=-2,x2=2.
当x∈(-∞,-2),(2,+∞)时,f′(x)>0,则f(x)单调递增;
当x∈(-2,2)时,f′(x)<0,则f(x)单调递减,
∴f(x)的极小值点为a=2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数f(x)=x3+ax2+bx+a2+a在x=1处有极值为7,则a等于
A.-3或3 B.3或-9 C.3 D.-3
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=3x2+2ax+b,
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-3
当a=-3,b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,x=1不是极值点.
∴a=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的值可以是
A.-4 B.-3 C.6 D.8
√
√
解析 由题意知f′(x)=3x2+2ax+(a+6)=0有两个不相等的根,
所以Δ=4a2-12(a+6)>0,
解得a>6或a<-3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.函数f(x)= 的极小值为_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f′(x)<0,得x<-2或x>1;
令f′(x)>0,得-2
在(-2,1)上单调递增,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点,则常数a=
_____.
经检验,符合题意.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.设函数f(x)=aln x+ +1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
由题意知,曲线在x=1处的切线斜率为0,即f′(1)=0,
解得a=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求函数f(x)的极值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当x∈(0,1)时,f′(x)<0,
故f(x)在(0,1)上单调递减;
当x∈(1,+∞)时,f′(x)>0,故f(x)在(1,+∞)上单调递增.
故f(x)在x=1处取得极小值,极小值为f(1)=3,无极大值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.设a为实数,函数f(x)=x3-x2-x+a.
(1)求f(x)的极值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=3x2-2x-1.
当x变化时,f′(x),f(x)的变化情况如下表:
极小值是f(1)=a-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当a在什么范围内取值时,曲线y=f(x)与x轴仅有一个交点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 函数f(x)=x3-x2-x+a
=(x-1)2(x+1)+a-1,
由此可知,x取足够大的正数时,有f(x)>0,
x取足够小的负数时,有f(x)<0,
∴曲线y=f(x)与x轴至少有一个交点.
f(x)极小值=f(1)=a-1.
∵曲线y=f(x)与x轴仅有一个交点,
∴f(x)极大值<0或f(x)极小值>0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=-2处取得极小值,则函数y=xf′(x)的图象可能是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f(x)在x=-2处取得极小值,
所以当x<-2时,
f(x)单调递减,
即f′(x)<0;
当x>-2时,f(x)单调递增,即f′(x)>0.
所以当x<-2时,y=xf′(x)>0;
当x=-2时,y=xf′(x)=0;
当-2<x<0时,y=xf′(x)<0;
当x=0时,y=xf′(x)=0;
当x>0时,y=xf′(x)>0.
结合选项中的图象知选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若函数f(x)=ex-ax-b在R上有小于0的极值点,则实数a的取值范围是
A.(-1,0) B.(0,1)
C.(-∞,-1) D.(1,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意知f′(x)=ex-a.
当a≤0时,f′(x)>0恒成立,则f(x)在R上单调递增,不符合题意;
当a>0时,令f′(x)=0,解得x=ln a,
∴当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
可知x=ln a为f(x)的极值点,∴ln a<0,∴a∈(0,1).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f′(x)=2x2-5ax+3a2,
由题意可得f′(3)=2×9-15a+3a2=0,
整理得a2-5a+6=0,解得a=2或a=3.
当a=2时,f′(x)=2x2-10x+12=2(x-2)(x-3),
令f′(x)>0,得x<2或x>3;
令f′(x)<0,得2
当a=3时,f′(x)=2x2-15x+27=(x-3)(2x-9).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
此时,函数y=f(x)在x=3处取得极大值,符合题意.
综上所述,a=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为______.
[1,5)
解析 ∵f′(x)=3x2+2x-a,
函数f(x)在区间(-1,1)上恰有一个极值点,
即f′(x)=0在(-1,1)内恰有一个根.
∴1≤a<5.
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知函数f(x)=ax3+bx2+cx的图象如图所示,且f(x)在x=x0与x=2处取得极值,则f(1)+f(-1)的值一定
A.等于0 B.大于0
C.小于0 D.小于或等于0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=3ax2+2bx+c.
令f′(x)=0,则x0和2是该方程的根.
由题图知,f′(x)<0的解集为(x0,2),
∴3a>0,则b>0,
∵f(1)+f(-1)=2b,
∴f(1)+f(-1)>0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
分以下两种情况讨论:
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,-2a) -2a (-2a,a-2) a-2 (a-2,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以f(x)在(-∞,-2a),(a-2,+∞)上单调递增,
在(-2a,a-2)上单调递减,函数f(x)在x=-2a处取得极大值f(-2a),
且f(-2a)=3ae-2a,
函数f(x)在x=a-2处取得极小值f(a-2),且f(a-2)=(4-3a)·ea-2.
当x变化时,f′(x),f(x)的变化情况如下表:
x (-∞,a-2) a-2 (a-2,-2a) -2a (-2a,+∞)
f′(x) + 0 - 0 +
f(x) ? 极大值 ? 极小值 ?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以f(x)在(-∞,a-2),(-2a,+∞)上单调递增,在(a-2,-2a)上单调递减,
函数f(x)在x=a-2处取得极大值f(a-2),
且f(a-2)=(4-3a)ea-2,
函数f(x)在x=-2a处取得极小值f(-2a),
且f(-2a)=3ae-2a.
