第五章 5.3.2 第2课时 函数的最大(小)值 课件(共68张PPT)
文档属性
| 名称 | 第五章 5.3.2 第2课时 函数的最大(小)值 课件(共68张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 07:32:22 | ||
图片预览










文档简介
(共68张PPT)
第2课时 函数的最大(小)值
第五章 5.3.2 函数的极值与最大(小)值
1.理解函数最值的概念,了解其与函数极值的区别与联系.
2.会求某闭区间上函数的最值.
学习目标
同学们,上节课我们在群山之间穿梭,感受了每一个山峰与山谷的优美之处,而今天我们誓要寻找最高的山峰和最低的峡谷,我们既要有俯视一切的雄心和气概,拿出“会当凌绝顶,一览众山小”的气势,也要有仰望一切的谦虚和胸怀,更要有“可上九天揽月,可下五洋捉鳖”的勇气,这其实就是我们今天要探究的函数的最值.
导语
随堂演练
课时对点练
一、极值与最值的关系
二、求函数的最值
三、利用最值证明不等式
内容索引
一、极值与最值的关系
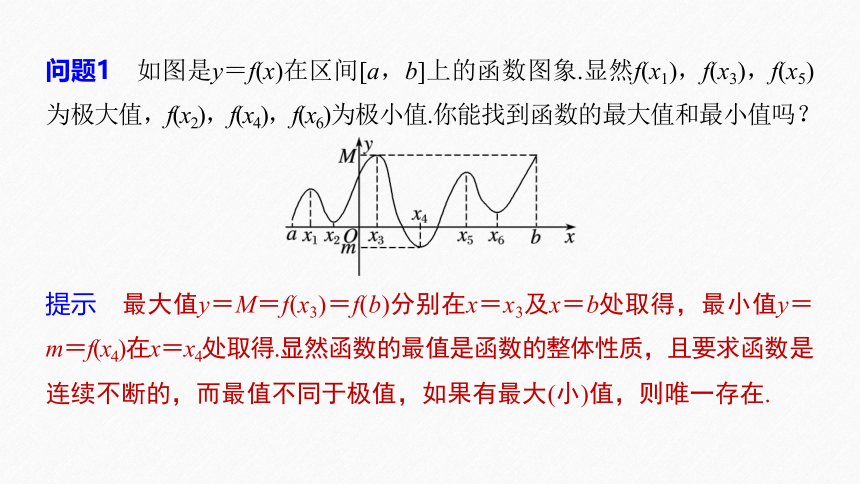
问题1 如图是y=f(x)在区间[a,b]上的函数图象.显然f(x1),f(x3),f(x5)为极大值,f(x2),f(x4),f(x6)为极小值.你能找到函数的最大值和最小值吗?
提示 最大值y=M=f(x3)=f(b)分别在x=x3及x=b处取得,最小值y=m=f(x4)在x=x4处取得.显然函数的最值是函数的整体性质,且要求函数是连续不断的,而最值不同于极值,如果有最大(小)值,则唯一存在.
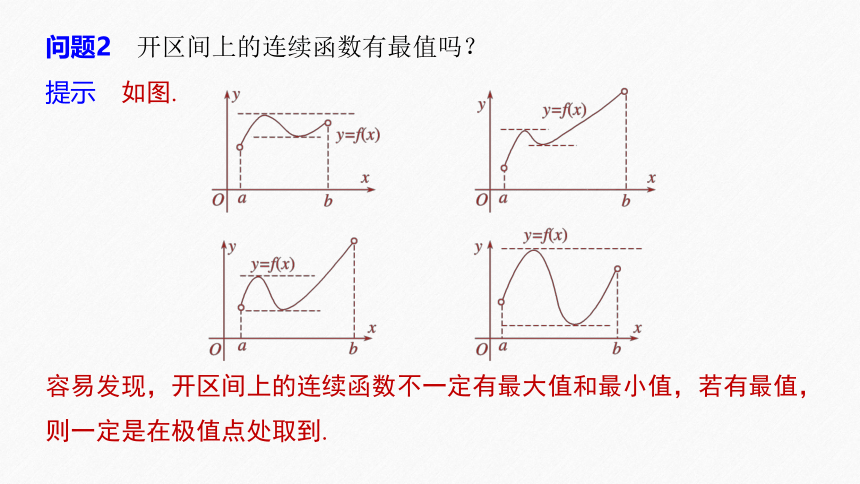
问题2 开区间上的连续函数有最值吗?
提示 如图.
容易发现,开区间上的连续函数不一定有最大值和最小值,若有最值,则一定是在极值点处取到.
知识梳理
函数最值的定义
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
(2)对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)≥f(x0),则称f(x0)为函数f(x)在区间I上的最小值;若对任意x∈I,存在x0∈I,使得f(x)≤f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
注意点:(1)开区间不一定有最值,闭区间上的连续函数一定有最值;(2)函数f(x)在闭区间[a,b]上连续是f(x)在闭区间[a,b]上有最大值和最小值的充分不必要条件.
例1 如图是函数y=f(x)在区间[a,b]上的图象,写出函数的极大值、极小值、最大值和最小值.
解 由题图可知,y=f(x)在x1,x3处取得极小值,在x2处取得极大值,所以极小值为f(x1),f(x3),极大值为f(x2);
比较极值和端点值可知函数的最小值是f(x3),最大值在b处取得,最大值为f(b).
反思感悟 最值与极值的区别与联系
(1)极值是对某一点附近(即局部)而言,最值是对函数的定义区间的整体而言.
(2)在函数的定义区间内,极大(小)值可能有多个,但最大(小)值只有一个(或者没有).
(3)函数f(x)的极值点为定义域中的内点,而最值点可以是区间的端点.
(4)对于可导函数,函数的最大(小)值必在极大(小)值点或区间端点处取得.
跟踪训练1 设f(x)是区间[a,b]上的连续函数,且在(a,b)内可导,则下列结论中正确的是
A.f(x)的极值点一定是最值点
B.f(x)的最值点一定是极值点
C.f(x)在区间[a,b]上可能没有极值点
D.f(x)在区间[a,b]上可能没有最值点
√
解析 根据函数的极值与最值的概念知,f(x)的极值点不一定是最值点,f(x)的最值点不一定是极值点.
可能是区间的端点,连续可导函数在闭区间上一定有最值,所以选项A,B,D都不正确,
若函数f(x)在区间[a,b]上单调,
则函数f(x)在区间[a,b]上没有极值点,所以C正确.
二、求函数的最值
例2 求下列函数的最值:
(1)f(x)=2x3-12x,x∈[-2,3];
解 因为f(x)=2x3-12x,x∈[-2,3],
所以f′(x)=6x2-12
令f′(x)=0,
因为f(-2)=8,f(3)=18,
当x=3时,f(x)取得最大值18.
(2)f(x)= x+sin x,x∈[0,2π].
又x∈[0,2π],
所以当x=0时,f(x)有最小值f(0)=0;
当x=2π时,f(x)有最大值f(2π)=π.
反思感悟 求函数最值的步骤
(1)求函数的定义域.
(2)求f′(x),解方程f′(x)=0.
(3)求极值、端点处的函数值,确定最值.
注意:不要忽略将所求极值与区间端点的函数值进行比较.
跟踪训练2 求下列函数的最值:
(1)f(x)=2x3-6x2+3,x∈[-2,4];
解 f′(x)=6x2-12x=6x(x-2).
令f′(x)=0,得x=0或x=2.
又f(0)=3,f(2)=-5,f(4)=35,f(-2)=-37,
∴当x=4时,f(x)取最大值35.
当x=-2时,f(x)取最小值-37.
即f(x)的最大值为35,最小值为-37.
当f′(x)=0时,x=2,
当x变化时,f′(x),f(x)的变化情况如表所示.
∴f(x)在(-∞,2)上单调递增,
在(2,+∞)上单调递减,
三、利用最值证明不等式
例3 已知函数f(x)=ex-e(ln x+1),求证f(x)≥0恒成立.
设F(x)=xex-e(x>0),则F(x)在(0,+∞)上单调递增,且F(1)=0.
f(x)的最小值为f(x)min=f(1)=0,∴f(x)≥0恒成立.
反思感悟 证不等式恒成立,用导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式直接构成函数,利用导数的方法,通过分类讨论研究函数的最值,即可得到结果.
∴当x>1时,g(x)-f(x)>0,即f(x)1.知识清单:
(1)函数最值的定义.
(2)求函数最值.
(3)函数最值的应用.
2.方法归纳:转化化归、分类讨论.
3.常见误区:忽视函数的最值与极值的区别与联系.
课堂小结
随堂演练
1
2
3
4
1.下列结论正确的是
A.若f(x)在[a,b]上有极大值,则极大值一定是[a,b]上的最大值
B.若f(x)在[a,b]上有极小值,则极小值一定是[a,b]上的最小值
C.若f(x)在[a,b]上有极大值,则极小值一定是在x=a和x=b处取得
D.若f(x)在[a,b]上连续,则f(x)在[a,b]上存在最大值和最小值
√
解析 函数f(x)在[a,b]上的极值不一定是最值,最值也不一定是极值,极值一定不会在端点处取得,而在[a,b]上一定存在最大值和最小值.
1
2
3
4
√
所以y的最大值为ymax=π-sin π=π.
1
2
3
4
3.函数f(x)=x3-3x(|x|<1)
A.有最值,但无极值
B.有最值,也有极值
C.既无最值,也无极值
D.无最值,但有极值
√
解析 f′(x)=3x2-3=3(x+1)(x-1),
当x∈(-1,1)时,f′(x)<0,
所以f(x)在(-1,1)上单调递减,
无最大值和最小值,也无极值.
1
2
3
4
4.函数f(x)=(x+1)ex的最小值是______.
解析 f(x)=(x+1)ex f′(x)=(x+2)ex,
当x>-2时,f′(x)>0,f(x)单调递增,
当x<-2时,f′(x)<0,f(x)单调递减,
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.设M,m分别是函数f(x)在[a,b]上的最大值和最小值,若M=m,则f′(x)
A.等于0 B.小于0 C.等于1 D.不确定
解析 因为M=m,
所以f(x)为常函数,
故f′(x)=0,故选A.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=1-2sin x,
所以sin x∈[-1,0],所以-2sin x∈[0,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x3-3x+1在区间[-3,0]上的最大值和最小值分别是
A.1,-1 B.1,-17 C.3,-17 D.9,-19
解析 f′(x)=3x2-3=3(x-1)(x+1),
令f′(x)=0,得x=±1.
又f(-3)=-27+9+1=-17,f(0)=1,
f(-1)=-1+3+1=3,1 [-3,0].
所以函数f(x)的最大值为3,最小值为-17.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.当0A.f 2(x)C.f(x)√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以根据对数函数的单调性可知,当00,
从而可得f′(x)>0,函数f(x)单调递增,
所以f(x2)所以有f(x2)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设h(x)=f(x)-g(x)
则h′(x)=x2-4x+3=(x-3)(x-1),
所以当x∈[1,3)时,h(x)单调递减;
当x∈(3,+∞)时,h(x)单调递增.
当x=3时,函数h(x)取得极小值也是最小值.
因为f(x)的图象始终在g(x)的图象上方,
所以h(x)min>0,即h(3)=a>0,
所以a的取值范围是(0,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由f(x)>0得0f′(x)=(2-x2)ex,
当x→-∞时,f(x)→0,
当x→+∞时,f(x)→-∞,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
结合函数的单调性可知,函数f(x)有最大值无最小值,
故C不正确,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若函数f(x)=x3-3x在区间[0,3]上的最大值、最小值分别为m,n,则m+n=______.
16
解析 f′(x)=3x2-3,
令f′(x)=0,得x=1或x=-1(舍去).
f(1)=-2.
又f(0)=0,f(3)=18,所以m=18,n=-2,m+n=16.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设0因为01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.求下列函数的最值:
(1)f(x)=sin x+cos x,x∈ ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=cos x-sin x.
令f′(x)=0,即tan x=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)f(x)=ln(1+x)- x2,x∈[0,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简为x2+x-2=0,
解得x1=-2(舍去),x2=1.
当0≤x<1时,f′(x)>0,f(x)单调递增;
当1又f(0)=0,f(2)=ln 3-1>0,f(1)>f(2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)=aln x-bx2,a,b∈R,且曲线y=f(x)在x=1处与直线y=- 相切.
(1)求a,b的值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求f(x)在 上的最大值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f′(x)>0,得01,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)A.f(a)-g(a) B.f(b)-g(b)
C.f(a)-g(b) D.f(b)-g(a)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 令F(x)=f(x)-g(x),
∵f′(x)∴F′(x)=f′(x)-g′(x)<0,
∴F(x)在[a,b]上单调递减,
∴F(x)max=F(a)=f(a)-g(a).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知函数f(x)=x3-3x-1,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是
A.20 B.18 C.3 D.0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f′(x)=3x2-3=3(x-1)(x+1),x∈[-3,2],
所以f(x)在[-1,1]上单调递减,
在[1,2]和[-3,-1]上单调递增.
f(-3)=-19,f(-1)=1,f(1)=-3,f(2)=1,
所以在区间[-3,2]上,f(x)max=1,f(x)min=-19,
又由题设知在[-3,2]上|f(x1)-f(x2)|≤f(x)max-f(x)min=20,
所以t≥20,故选A.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当00;
当x>e时,g′(x)<0;
故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知函数f(x)=- x3+2ax2+3x(a>0)的导数f′(x)的最大值为5,则函数f(x)在点(1,f(1))处的切线方程是______________.
15x-3y-2=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f′(x)=-2x2+4ax+3
=-2(x-a)2+3+2a2,
∴f′(x)max=3+2a2=5,
∵a>0,∴a=1.
∴f′(x)=-2x2+4x+3,
f′(1)=-2+4+3=5.
即15x-3y-2=0.
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知f(x)=-x2+mx+1在区间(-2,-1)上的最大值就是函数f(x)的极大值,则m的取值范围是___________.
(-4,-2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.已知函数f(x)=ex-x2-ax.
(1)当a=-1时,求函数f(x)在点(1,f(1))处的切线方程;
解 f′(x)=ex-2x+1,f′(1)=e-1,f(1)=e,
切线方程为y-e=(e-1)(x-1),
即y=(e-1)x+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当x>0时,f(x)≥1-x恒成立,求实数a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设F(x)=ex-x-1,F′(x)=ex-1,x∈(0,+∞),F′(x)=ex-1>0,
所以F(x)min>0,所以当x∈(0,1)时,g′(x)<0,g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,
故g(x)min=g(1)=e-1,
第2课时 函数的最大(小)值
第五章 5.3.2 函数的极值与最大(小)值
1.理解函数最值的概念,了解其与函数极值的区别与联系.
2.会求某闭区间上函数的最值.
学习目标
同学们,上节课我们在群山之间穿梭,感受了每一个山峰与山谷的优美之处,而今天我们誓要寻找最高的山峰和最低的峡谷,我们既要有俯视一切的雄心和气概,拿出“会当凌绝顶,一览众山小”的气势,也要有仰望一切的谦虚和胸怀,更要有“可上九天揽月,可下五洋捉鳖”的勇气,这其实就是我们今天要探究的函数的最值.
导语
随堂演练
课时对点练
一、极值与最值的关系
二、求函数的最值
三、利用最值证明不等式
内容索引
一、极值与最值的关系
问题1 如图是y=f(x)在区间[a,b]上的函数图象.显然f(x1),f(x3),f(x5)为极大值,f(x2),f(x4),f(x6)为极小值.你能找到函数的最大值和最小值吗?
提示 最大值y=M=f(x3)=f(b)分别在x=x3及x=b处取得,最小值y=m=f(x4)在x=x4处取得.显然函数的最值是函数的整体性质,且要求函数是连续不断的,而最值不同于极值,如果有最大(小)值,则唯一存在.
问题2 开区间上的连续函数有最值吗?
提示 如图.
容易发现,开区间上的连续函数不一定有最大值和最小值,若有最值,则一定是在极值点处取到.
知识梳理
函数最值的定义
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
(2)对于函数f(x),给定区间I,若对任意x∈I,存在x0∈I,使得f(x)≥f(x0),则称f(x0)为函数f(x)在区间I上的最小值;若对任意x∈I,存在x0∈I,使得f(x)≤f(x0),则称f(x0)为函数f(x)在区间I上的最大值.
注意点:(1)开区间不一定有最值,闭区间上的连续函数一定有最值;(2)函数f(x)在闭区间[a,b]上连续是f(x)在闭区间[a,b]上有最大值和最小值的充分不必要条件.
例1 如图是函数y=f(x)在区间[a,b]上的图象,写出函数的极大值、极小值、最大值和最小值.
解 由题图可知,y=f(x)在x1,x3处取得极小值,在x2处取得极大值,所以极小值为f(x1),f(x3),极大值为f(x2);
比较极值和端点值可知函数的最小值是f(x3),最大值在b处取得,最大值为f(b).
反思感悟 最值与极值的区别与联系
(1)极值是对某一点附近(即局部)而言,最值是对函数的定义区间的整体而言.
(2)在函数的定义区间内,极大(小)值可能有多个,但最大(小)值只有一个(或者没有).
(3)函数f(x)的极值点为定义域中的内点,而最值点可以是区间的端点.
(4)对于可导函数,函数的最大(小)值必在极大(小)值点或区间端点处取得.
跟踪训练1 设f(x)是区间[a,b]上的连续函数,且在(a,b)内可导,则下列结论中正确的是
A.f(x)的极值点一定是最值点
B.f(x)的最值点一定是极值点
C.f(x)在区间[a,b]上可能没有极值点
D.f(x)在区间[a,b]上可能没有最值点
√
解析 根据函数的极值与最值的概念知,f(x)的极值点不一定是最值点,f(x)的最值点不一定是极值点.
可能是区间的端点,连续可导函数在闭区间上一定有最值,所以选项A,B,D都不正确,
若函数f(x)在区间[a,b]上单调,
则函数f(x)在区间[a,b]上没有极值点,所以C正确.
二、求函数的最值
例2 求下列函数的最值:
(1)f(x)=2x3-12x,x∈[-2,3];
解 因为f(x)=2x3-12x,x∈[-2,3],
所以f′(x)=6x2-12
令f′(x)=0,
因为f(-2)=8,f(3)=18,
当x=3时,f(x)取得最大值18.
(2)f(x)= x+sin x,x∈[0,2π].
又x∈[0,2π],
所以当x=0时,f(x)有最小值f(0)=0;
当x=2π时,f(x)有最大值f(2π)=π.
反思感悟 求函数最值的步骤
(1)求函数的定义域.
(2)求f′(x),解方程f′(x)=0.
(3)求极值、端点处的函数值,确定最值.
注意:不要忽略将所求极值与区间端点的函数值进行比较.
跟踪训练2 求下列函数的最值:
(1)f(x)=2x3-6x2+3,x∈[-2,4];
解 f′(x)=6x2-12x=6x(x-2).
令f′(x)=0,得x=0或x=2.
又f(0)=3,f(2)=-5,f(4)=35,f(-2)=-37,
∴当x=4时,f(x)取最大值35.
当x=-2时,f(x)取最小值-37.
即f(x)的最大值为35,最小值为-37.
当f′(x)=0时,x=2,
当x变化时,f′(x),f(x)的变化情况如表所示.
∴f(x)在(-∞,2)上单调递增,
在(2,+∞)上单调递减,
三、利用最值证明不等式
例3 已知函数f(x)=ex-e(ln x+1),求证f(x)≥0恒成立.
设F(x)=xex-e(x>0),则F(x)在(0,+∞)上单调递增,且F(1)=0.
f(x)的最小值为f(x)min=f(1)=0,∴f(x)≥0恒成立.
反思感悟 证不等式恒成立,用导数的方法求出函数的最值,进而可求出结果;有时也可根据不等式直接构成函数,利用导数的方法,通过分类讨论研究函数的最值,即可得到结果.
∴当x>1时,g(x)-f(x)>0,即f(x)
(1)函数最值的定义.
(2)求函数最值.
(3)函数最值的应用.
2.方法归纳:转化化归、分类讨论.
3.常见误区:忽视函数的最值与极值的区别与联系.
课堂小结
随堂演练
1
2
3
4
1.下列结论正确的是
A.若f(x)在[a,b]上有极大值,则极大值一定是[a,b]上的最大值
B.若f(x)在[a,b]上有极小值,则极小值一定是[a,b]上的最小值
C.若f(x)在[a,b]上有极大值,则极小值一定是在x=a和x=b处取得
D.若f(x)在[a,b]上连续,则f(x)在[a,b]上存在最大值和最小值
√
解析 函数f(x)在[a,b]上的极值不一定是最值,最值也不一定是极值,极值一定不会在端点处取得,而在[a,b]上一定存在最大值和最小值.
1
2
3
4
√
所以y的最大值为ymax=π-sin π=π.
1
2
3
4
3.函数f(x)=x3-3x(|x|<1)
A.有最值,但无极值
B.有最值,也有极值
C.既无最值,也无极值
D.无最值,但有极值
√
解析 f′(x)=3x2-3=3(x+1)(x-1),
当x∈(-1,1)时,f′(x)<0,
所以f(x)在(-1,1)上单调递减,
无最大值和最小值,也无极值.
1
2
3
4
4.函数f(x)=(x+1)ex的最小值是______.
解析 f(x)=(x+1)ex f′(x)=(x+2)ex,
当x>-2时,f′(x)>0,f(x)单调递增,
当x<-2时,f′(x)<0,f(x)单调递减,
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.设M,m分别是函数f(x)在[a,b]上的最大值和最小值,若M=m,则f′(x)
A.等于0 B.小于0 C.等于1 D.不确定
解析 因为M=m,
所以f(x)为常函数,
故f′(x)=0,故选A.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 f′(x)=1-2sin x,
所以sin x∈[-1,0],所以-2sin x∈[0,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.函数f(x)=x3-3x+1在区间[-3,0]上的最大值和最小值分别是
A.1,-1 B.1,-17 C.3,-17 D.9,-19
解析 f′(x)=3x2-3=3(x-1)(x+1),
令f′(x)=0,得x=±1.
又f(-3)=-27+9+1=-17,f(0)=1,
f(-1)=-1+3+1=3,1 [-3,0].
所以函数f(x)的最大值为3,最小值为-17.
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.当0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以根据对数函数的单调性可知,当0
从而可得f′(x)>0,函数f(x)单调递增,
所以f(x2)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 设h(x)=f(x)-g(x)
则h′(x)=x2-4x+3=(x-3)(x-1),
所以当x∈[1,3)时,h(x)单调递减;
当x∈(3,+∞)时,h(x)单调递增.
当x=3时,函数h(x)取得极小值也是最小值.
因为f(x)的图象始终在g(x)的图象上方,
所以h(x)min>0,即h(3)=a>0,
所以a的取值范围是(0,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由f(x)>0得0
当x→-∞时,f(x)→0,
当x→+∞时,f(x)→-∞,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
结合函数的单调性可知,函数f(x)有最大值无最小值,
故C不正确,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.若函数f(x)=x3-3x在区间[0,3]上的最大值、最小值分别为m,n,则m+n=______.
16
解析 f′(x)=3x2-3,
令f′(x)=0,得x=1或x=-1(舍去).
f(1)=-2.
又f(0)=0,f(3)=18,所以m=18,n=-2,m+n=16.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.设0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.求下列函数的最值:
(1)f(x)=sin x+cos x,x∈ ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 f′(x)=cos x-sin x.
令f′(x)=0,即tan x=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)f(x)=ln(1+x)- x2,x∈[0,2].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
化简为x2+x-2=0,
解得x1=-2(舍去),x2=1.
当0≤x<1时,f′(x)>0,f(x)单调递增;
当1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知函数f(x)=aln x-bx2,a,b∈R,且曲线y=f(x)在x=1处与直线y=- 相切.
(1)求a,b的值;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求f(x)在 上的最大值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
令f′(x)>0,得0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
综合运用
16
11.已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)
C.f(a)-g(b) D.f(b)-g(a)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 令F(x)=f(x)-g(x),
∵f′(x)
∴F(x)在[a,b]上单调递减,
∴F(x)max=F(a)=f(a)-g(a).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.已知函数f(x)=x3-3x-1,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是
A.20 B.18 C.3 D.0
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为f′(x)=3x2-3=3(x-1)(x+1),x∈[-3,2],
所以f(x)在[-1,1]上单调递减,
在[1,2]和[-3,-1]上单调递增.
f(-3)=-19,f(-1)=1,f(1)=-3,f(2)=1,
所以在区间[-3,2]上,f(x)max=1,f(x)min=-19,
又由题设知在[-3,2]上|f(x1)-f(x2)|≤f(x)max-f(x)min=20,
所以t≥20,故选A.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当0
当x>e时,g′(x)<0;
故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知函数f(x)=- x3+2ax2+3x(a>0)的导数f′(x)的最大值为5,则函数f(x)在点(1,f(1))处的切线方程是______________.
15x-3y-2=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵f′(x)=-2x2+4ax+3
=-2(x-a)2+3+2a2,
∴f′(x)max=3+2a2=5,
∵a>0,∴a=1.
∴f′(x)=-2x2+4x+3,
f′(1)=-2+4+3=5.
即15x-3y-2=0.
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知f(x)=-x2+mx+1在区间(-2,-1)上的最大值就是函数f(x)的极大值,则m的取值范围是___________.
(-4,-2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.已知函数f(x)=ex-x2-ax.
(1)当a=-1时,求函数f(x)在点(1,f(1))处的切线方程;
解 f′(x)=ex-2x+1,f′(1)=e-1,f(1)=e,
切线方程为y-e=(e-1)(x-1),
即y=(e-1)x+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当x>0时,f(x)≥1-x恒成立,求实数a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设F(x)=ex-x-1,F′(x)=ex-1,x∈(0,+∞),F′(x)=ex-1>0,
所以F(x)min>0,所以当x∈(0,1)时,g′(x)<0,g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,
故g(x)min=g(1)=e-1,
