方程的根与函数的零点课件
图片预览







文档简介
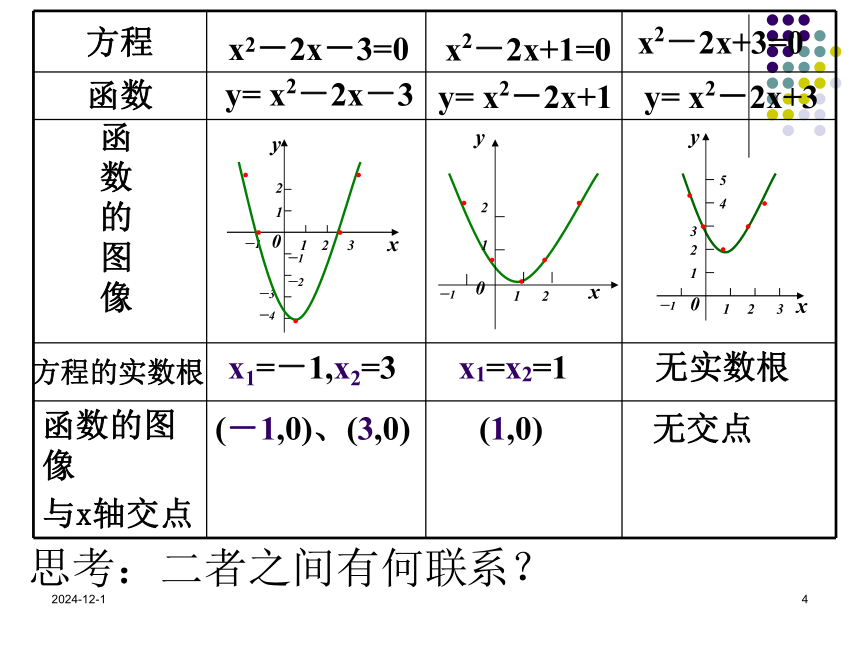
课件47张PPT。2019/1/91方程的根与函数的零点2019/1/922019/1/932019/1/94方程函数函
数
的
图像方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点2019/1/952019/1/96有两个不等的
实数根x1,x2
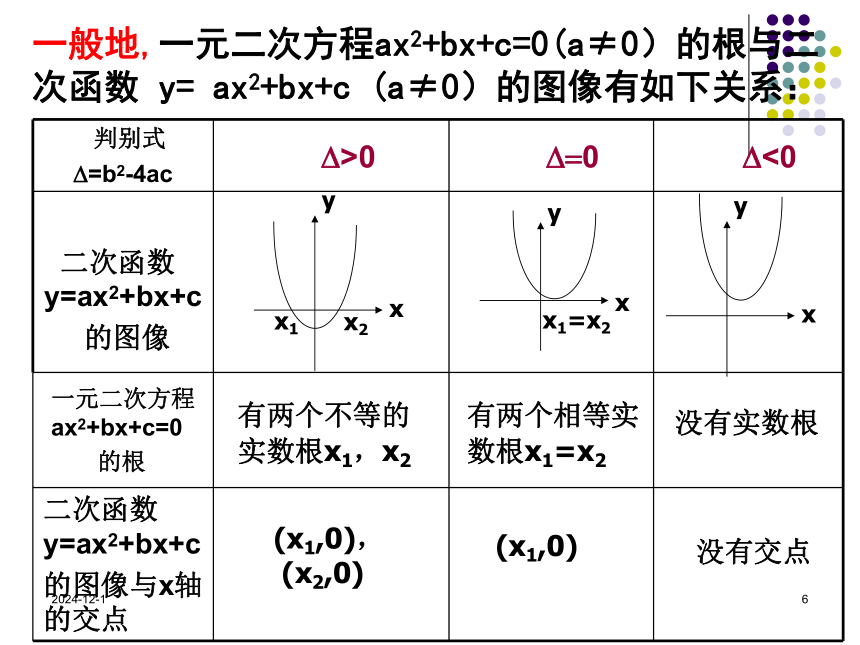
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图像有如下关系:(x1,0),
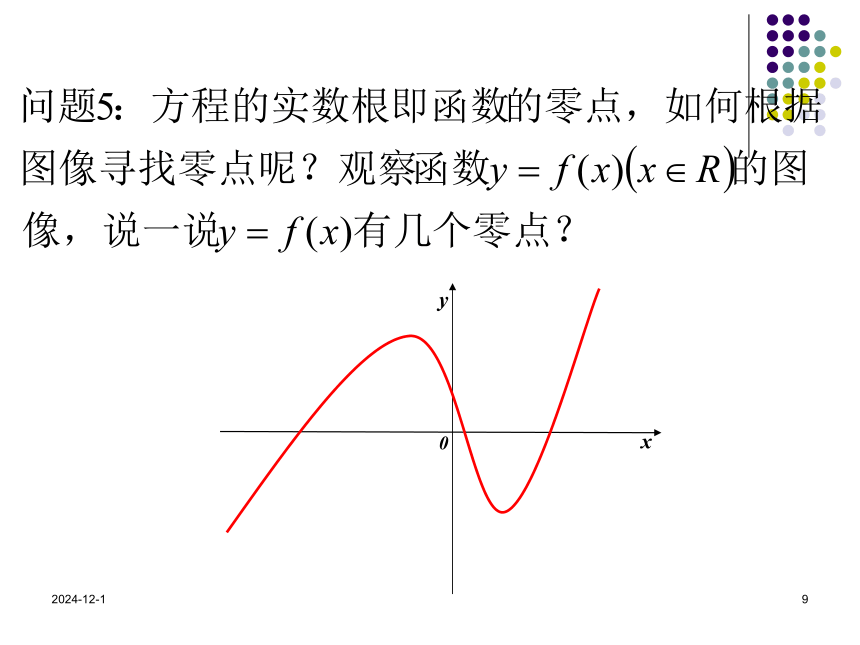
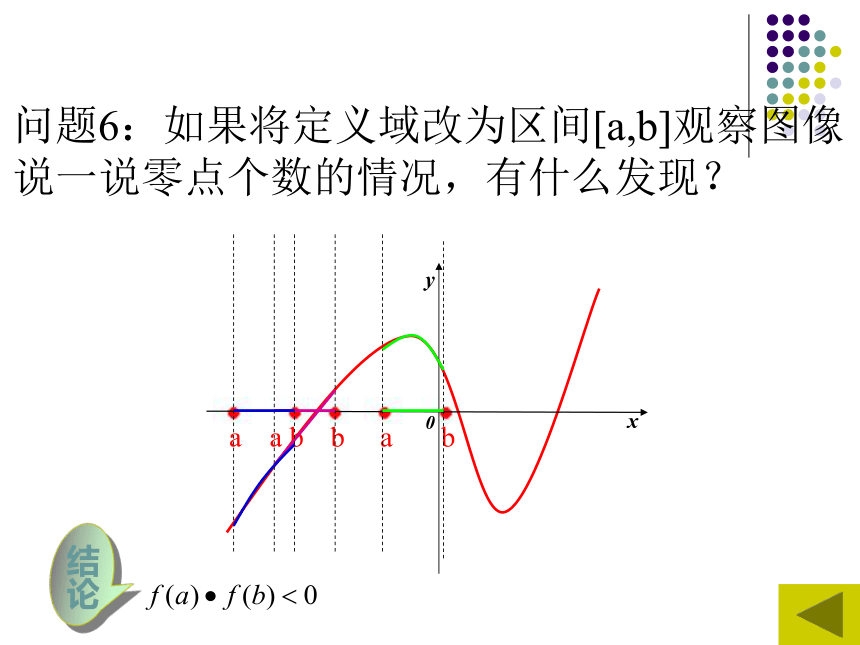
(x2,0) (x1,0)没有交点2019/1/972019/1/981、函数零点的定义对于函数 ,我们把使 的实数x 叫做函数 的零点。方程f(x)=0有实数根2、结论2019/1/992019/1/910问题6:如果将定义域改为区间[a,b]观察图像
说一说零点个数的情况,有什么发现?2019/1/9112019/1/912问题8:满足上述两个条件,能否确定零点
个数呢?2019/1/913结论2019/1/914表3--1 x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 解:用计算器或计算机作出 的对应值表(表3--1)和图像。2019/1/915问题10:为什么上个问题中只有一个零点呢?
说一说理由?2019/1/916问题11:请同学们思考、交流一下,这节课
学习到了什么?1、知识小结:一个定义,四个结论。2、思想方法:数形结合、转化思想。2019/1/917作业:1、必做题:P88 练习第二题2、选做题:(1) 在区间(0,3)范围内恰有一个零点,则a的取值范围是多少?2019/1/918目 录一、教材、学情分析二、教学目标、重难点分析三、教法、学法分析四、教学流程2019/1/919一、教材结构与内容简析 函数与方程思想是中学数学的重要思想。
本节是在学习了前两章函数性质的基础上,利用函数的图象和性质来判断方程的根的存在性及根的个数,从而了解函数的零点与方程的根的关系以及掌握函数在某个区间上存在零点的判定方法;为下节“二分法求方程的近似解”和后续学习的算法提供基础.
因此本节内容具有承前启后的作用,非常重要. 2019/1/920二、学情分析 在此之前,学生对一元二次函数和一元二次方程已经比较熟悉,会判断具体的一元二次方程有没有根,有几个根,会用求根公式求根。
但是对一元二次函数与方程的联系认识不全面,也没有上升到一般的函数与方程的层次。
因此,在讲解本节内容时,让学生对函数与方程的关系及零点存在定理有较为全面的认识。2019/1/921二、教学目标(一)认知目标:
1.理解函数的零点与方程的根的联系.
2.理解并会用零点存在定理判断函数的零点.
(二)能力目标:
体会数形结合思想,转化思想以及函数与方程思想的意义和价值,培养学生自主发现、探究实践的能力.
(三)情感目标:
培养学生锲而不舍的探索精神和严密思考的良好学习习惯。2019/1/922三、教学重点、难点教学重点:理解函数的零点与方程的根
之间的联系,掌握零点存在
的判定条件. 教学难点:探究发现函数零点的存在性.2019/1/923四、教法分析教法上,以问题为纽带,用问题引出内容,激发学生积极主动地进行探索;同时向学生渗透问题意识,培养学生发现问题、解决问题的能力。
采用 “提出问题——引导探究——得出结论——实际应用”的教与学模式.2019/1/924五、教学过程提出问题,激发学生思考函数零点概念零点存在定理巩固及应用总结提升课后作业巩固及应用2019/1/925一些复杂的方程无法求解,造成学生的认知冲突,引发学生的好奇心和求知欲。此时开门见山的提出用函数的思想解决方程根的问题,点明本节课的课题。 (一)设问激疑,引出课题设计意图五、教学过程求方程3x2 - 6 x+1=0的实数根 变式:求下列方程的实数根
3x3 - 6x+1=0 问题1:lnx+2x-6=02019/1/926(二)启发引导,逐步深入五、教学过程设计意图以问题激发学生思考,将大问题分解为几个小问题,自然地得到函数和方程的初步认识。
让学生体会到如何分析问题。一元二次方程ax2+bx+c=0(a≠0)
与二次函数y=ax2+bx+c(a≠0)有什么联系?问题2:子问题:形式上有什么相同点?有什么不同点?怎样可以由函数得到方程?2019/1/927(三)数形结合,巩固认识 五、教学过程设计意图 以实例说明方程、函数、函数图象三者的关系,渗透数形结合的思想。为引入函数零点的概念打下基础。方程的根函数值y=0时的x的值函数图象与x轴交点的横坐标x1=-1,
x2=3(-1,0)
(3,0)板书2019/1/928五、教学过程设计意图 从具体到一般,从简单到复杂,培养学生的思维能力和归纳能力. (三)数形结合,巩固认识 2019/1/929五、教学过程设计意图自然地得出函数零点的概念。 (四)顺水推舟,得出概念 方程f(x)=0
的实数根2019/1/930五、教学过程设计意图自然地得出等价关系。 (四)顺水推舟,得出概念 方程f(x)=0
有实数根2019/1/9311. 会判断函数是否有零点;
2.会用解方程的方法求简单的函数零点;
3.体会方程与函数的联系;
4.明确函数的零点是一个实数。(五)概念辨析,巩固新知设计意图五、教学过程判断下列函数是否有零点,若有,请求出2019/1/932设计意图五、教学过程(六)提出问题,探索零点存在定理 问3:
函数y=lnx+2x-6的零点存在吗?
若存在,大致在什么区间?用什么判断?用图象!激发思考2019/1/933设计意图五、教学过程将函数的零点转化到图象上来,使抽象的问题直观化,更利于学生理解定理的本质.
探索定理的过程中,通过正看、逆看、换条件看,培养学生缜密思考的良好习惯。ab x ab x1. 一定有?有几个?一定没有?2.如果图象不是连续不断的,能否一定有?让学生动手画3.怎样用数学符号表示零点存在的条件?(六)探索零点存在定理 2019/1/934设计意图五、教学过程定理的发现过程体现了数形结合的思想和转化的思想。函数零点 函数图象
端点处函数值符号(六)零点存在定理 2019/1/935设计意图五、教学过程(七)定理应用 通过反馈练习,使学生会直接应用定理找出函数零点.巩固练习:已知函数f(x)的图象
是连续不断的,有如下的x,f(x)
对应值表:
函数在区间[1,6]上的零点
至少有 个 2019/1/936设计意图五、教学过程(七)定理应用 通过反馈练习,使学生初步运用定理找出函数零点所在区间.练习2、求证:方程5x2-7x-1=0
的一个根在区间(-1,0)内,
另一个根在区间(1,2)内。2019/1/937 引导学生用定理解决问题,然后利用函数单调性判断零点的个数,并借助函数图象对整个解题思路有一个直观的认识. 设计意图五、教学过程(七)定理应用例1.求函数f(x)=lnx+2x-6的
零点个数。思路:
用定理判断存在?手算用1,e等特殊值计算可介绍用两个图像的交点
来判断函数的零点?用单调性判断零点个数2019/1/938用零点存在定理解决问题,同时反映教学效果,便于查漏补缺. (八)巩固知识,尝试练习设计意图五、教学过程2、函数 的零点
所在的大致区间是( )A、(1,2) B、(2,3)
C、(3,4) D、(e,+∞)2019/1/9391.你能说说函数的零点与方程的根的联系吗?
2.如果函数图象在区间[a,b]上是连续不断的,那么在什么条件下,函数在(a,b)内有零点?优化学生的认知结构,把课堂所学内容内化为学生的自己的知识和能力. (九)总结提升设计意图五、教学过程问题4:内容小结:1.函数零点的定义
2.等价关系
3.零点存在定理 方程f(x)=0的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点2019/1/940(十)课后作业设计意图五、教学过程 巩固学生所学的新知识,将学生的思维向外延伸,激发学生的发散思维. 2019/1/941板书设计2019/1/942 对新知识的理解需要一个不断深化完善的过程,通过练习,进行数学思想方法的小结,可使学生更深刻地理解数学思想方法在解题中的地位和应用,(八)巩固知识,尝试练习设计意图五、教学过程2、函数 的零点
所在的大致区间是( )A、(1,2) B、(2,3)
C、(3,4) D、(e,+∞)2019/1/9432019/1/9442019/1/945设计意图五、教学过程(五)剖析零点存在定理 通过改变定理的条件,激发学生思考,使学生对定理有全面的理解。
培养学生缜密分析问题的思维品质。
让学生自己画,并请学生画在黑板上。
abab1.是不是一定有?一定没有?有几个?2.条件如果是不连续的,能否一定有?2019/1/946设计意图五、教学过程(四)另辟蹊径,探索零点存在定理 将函数的零点转化到图象上来,使抽象的问题直观化,更利于学生理解定理的本质.
对定理正看、逆看、换条件看,培养学生缜密思考的良好习惯。ab x ab x1.是不是一定有?一定没有?有几个?2.条件如果是不连续的,能否一定有?让学生动手画3.怎样用数学符号表示零点存在的条件?2019/1/947五、教学过程设问激疑,创设情景启发引导,形成概念(三)初步运用,示例练习(四)讨论探究,揭示定理(五)观察感知,例题学习(七)反思小结,培养能力(八)课后作业,自主学习(六)知识应用,尝试练习
数
的
图像方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点2019/1/952019/1/96有两个不等的
实数根x1,x2
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图像有如下关系:(x1,0),
(x2,0) (x1,0)没有交点2019/1/972019/1/981、函数零点的定义对于函数 ,我们把使 的实数x 叫做函数 的零点。方程f(x)=0有实数根2、结论2019/1/992019/1/910问题6:如果将定义域改为区间[a,b]观察图像
说一说零点个数的情况,有什么发现?2019/1/9112019/1/912问题8:满足上述两个条件,能否确定零点
个数呢?2019/1/913结论2019/1/914表3--1 x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 解:用计算器或计算机作出 的对应值表(表3--1)和图像。2019/1/915问题10:为什么上个问题中只有一个零点呢?
说一说理由?2019/1/916问题11:请同学们思考、交流一下,这节课
学习到了什么?1、知识小结:一个定义,四个结论。2、思想方法:数形结合、转化思想。2019/1/917作业:1、必做题:P88 练习第二题2、选做题:(1) 在区间(0,3)范围内恰有一个零点,则a的取值范围是多少?2019/1/918目 录一、教材、学情分析二、教学目标、重难点分析三、教法、学法分析四、教学流程2019/1/919一、教材结构与内容简析 函数与方程思想是中学数学的重要思想。
本节是在学习了前两章函数性质的基础上,利用函数的图象和性质来判断方程的根的存在性及根的个数,从而了解函数的零点与方程的根的关系以及掌握函数在某个区间上存在零点的判定方法;为下节“二分法求方程的近似解”和后续学习的算法提供基础.
因此本节内容具有承前启后的作用,非常重要. 2019/1/920二、学情分析 在此之前,学生对一元二次函数和一元二次方程已经比较熟悉,会判断具体的一元二次方程有没有根,有几个根,会用求根公式求根。
但是对一元二次函数与方程的联系认识不全面,也没有上升到一般的函数与方程的层次。
因此,在讲解本节内容时,让学生对函数与方程的关系及零点存在定理有较为全面的认识。2019/1/921二、教学目标(一)认知目标:
1.理解函数的零点与方程的根的联系.
2.理解并会用零点存在定理判断函数的零点.
(二)能力目标:
体会数形结合思想,转化思想以及函数与方程思想的意义和价值,培养学生自主发现、探究实践的能力.
(三)情感目标:
培养学生锲而不舍的探索精神和严密思考的良好学习习惯。2019/1/922三、教学重点、难点教学重点:理解函数的零点与方程的根
之间的联系,掌握零点存在
的判定条件. 教学难点:探究发现函数零点的存在性.2019/1/923四、教法分析教法上,以问题为纽带,用问题引出内容,激发学生积极主动地进行探索;同时向学生渗透问题意识,培养学生发现问题、解决问题的能力。
采用 “提出问题——引导探究——得出结论——实际应用”的教与学模式.2019/1/924五、教学过程提出问题,激发学生思考函数零点概念零点存在定理巩固及应用总结提升课后作业巩固及应用2019/1/925一些复杂的方程无法求解,造成学生的认知冲突,引发学生的好奇心和求知欲。此时开门见山的提出用函数的思想解决方程根的问题,点明本节课的课题。 (一)设问激疑,引出课题设计意图五、教学过程求方程3x2 - 6 x+1=0的实数根 变式:求下列方程的实数根
3x3 - 6x+1=0 问题1:lnx+2x-6=02019/1/926(二)启发引导,逐步深入五、教学过程设计意图以问题激发学生思考,将大问题分解为几个小问题,自然地得到函数和方程的初步认识。
让学生体会到如何分析问题。一元二次方程ax2+bx+c=0(a≠0)
与二次函数y=ax2+bx+c(a≠0)有什么联系?问题2:子问题:形式上有什么相同点?有什么不同点?怎样可以由函数得到方程?2019/1/927(三)数形结合,巩固认识 五、教学过程设计意图 以实例说明方程、函数、函数图象三者的关系,渗透数形结合的思想。为引入函数零点的概念打下基础。方程的根函数值y=0时的x的值函数图象与x轴交点的横坐标x1=-1,
x2=3(-1,0)
(3,0)板书2019/1/928五、教学过程设计意图 从具体到一般,从简单到复杂,培养学生的思维能力和归纳能力. (三)数形结合,巩固认识 2019/1/929五、教学过程设计意图自然地得出函数零点的概念。 (四)顺水推舟,得出概念 方程f(x)=0
的实数根2019/1/930五、教学过程设计意图自然地得出等价关系。 (四)顺水推舟,得出概念 方程f(x)=0
有实数根2019/1/9311. 会判断函数是否有零点;
2.会用解方程的方法求简单的函数零点;
3.体会方程与函数的联系;
4.明确函数的零点是一个实数。(五)概念辨析,巩固新知设计意图五、教学过程判断下列函数是否有零点,若有,请求出2019/1/932设计意图五、教学过程(六)提出问题,探索零点存在定理 问3:
函数y=lnx+2x-6的零点存在吗?
若存在,大致在什么区间?用什么判断?用图象!激发思考2019/1/933设计意图五、教学过程将函数的零点转化到图象上来,使抽象的问题直观化,更利于学生理解定理的本质.
探索定理的过程中,通过正看、逆看、换条件看,培养学生缜密思考的良好习惯。ab x ab x1. 一定有?有几个?一定没有?2.如果图象不是连续不断的,能否一定有?让学生动手画3.怎样用数学符号表示零点存在的条件?(六)探索零点存在定理 2019/1/934设计意图五、教学过程定理的发现过程体现了数形结合的思想和转化的思想。函数零点 函数图象
端点处函数值符号(六)零点存在定理 2019/1/935设计意图五、教学过程(七)定理应用 通过反馈练习,使学生会直接应用定理找出函数零点.巩固练习:已知函数f(x)的图象
是连续不断的,有如下的x,f(x)
对应值表:
函数在区间[1,6]上的零点
至少有 个 2019/1/936设计意图五、教学过程(七)定理应用 通过反馈练习,使学生初步运用定理找出函数零点所在区间.练习2、求证:方程5x2-7x-1=0
的一个根在区间(-1,0)内,
另一个根在区间(1,2)内。2019/1/937 引导学生用定理解决问题,然后利用函数单调性判断零点的个数,并借助函数图象对整个解题思路有一个直观的认识. 设计意图五、教学过程(七)定理应用例1.求函数f(x)=lnx+2x-6的
零点个数。思路:
用定理判断存在?手算用1,e等特殊值计算可介绍用两个图像的交点
来判断函数的零点?用单调性判断零点个数2019/1/938用零点存在定理解决问题,同时反映教学效果,便于查漏补缺. (八)巩固知识,尝试练习设计意图五、教学过程2、函数 的零点
所在的大致区间是( )A、(1,2) B、(2,3)
C、(3,4) D、(e,+∞)2019/1/9391.你能说说函数的零点与方程的根的联系吗?
2.如果函数图象在区间[a,b]上是连续不断的,那么在什么条件下,函数在(a,b)内有零点?优化学生的认知结构,把课堂所学内容内化为学生的自己的知识和能力. (九)总结提升设计意图五、教学过程问题4:内容小结:1.函数零点的定义
2.等价关系
3.零点存在定理 方程f(x)=0的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点2019/1/940(十)课后作业设计意图五、教学过程 巩固学生所学的新知识,将学生的思维向外延伸,激发学生的发散思维. 2019/1/941板书设计2019/1/942 对新知识的理解需要一个不断深化完善的过程,通过练习,进行数学思想方法的小结,可使学生更深刻地理解数学思想方法在解题中的地位和应用,(八)巩固知识,尝试练习设计意图五、教学过程2、函数 的零点
所在的大致区间是( )A、(1,2) B、(2,3)
C、(3,4) D、(e,+∞)2019/1/9432019/1/9442019/1/945设计意图五、教学过程(五)剖析零点存在定理 通过改变定理的条件,激发学生思考,使学生对定理有全面的理解。
培养学生缜密分析问题的思维品质。
让学生自己画,并请学生画在黑板上。
abab1.是不是一定有?一定没有?有几个?2.条件如果是不连续的,能否一定有?2019/1/946设计意图五、教学过程(四)另辟蹊径,探索零点存在定理 将函数的零点转化到图象上来,使抽象的问题直观化,更利于学生理解定理的本质.
对定理正看、逆看、换条件看,培养学生缜密思考的良好习惯。ab x ab x1.是不是一定有?一定没有?有几个?2.条件如果是不连续的,能否一定有?让学生动手画3.怎样用数学符号表示零点存在的条件?2019/1/947五、教学过程设问激疑,创设情景启发引导,形成概念(三)初步运用,示例练习(四)讨论探究,揭示定理(五)观察感知,例题学习(七)反思小结,培养能力(八)课后作业,自主学习(六)知识应用,尝试练习
