高中数学人教A版2019必修第二册 10.3 《频率与概率》名师课件(共32张PPT)
文档属性
| 名称 | 高中数学人教A版2019必修第二册 10.3 《频率与概率》名师课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1003.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 08:12:30 | ||
图片预览









文档简介
(共32张PPT)
即两个相互独立事件同时发生的概率,等于每个事件发生的概率的积.
2.推广:如果事件相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的积.即:
1.若是相互独立事件,则有
相互独立事件同时发生的概率公式
复习引入
人教A版同步教材名师课件
频率与概率
学习目标
学 习 目 标 核心素养
结合实例,会用频率估计概率 数学分析
了解随机模拟,会用随机模拟的方法估计事件的概率 数学运算
学习目标
课程目标:
1.通过实验让学生理解当试验次数较大时,实验频率稳定在某一常数附近,并据此
能估计出某一事件发生的频率.
2.通过对实际问题的分析,培养使用数学的良好意识,激发学习兴趣,体验数学的应用价值.
学科素养:
1.数学建模:概率的应用
2.逻辑推理:频率与概率的关系
3.数学运算:频率与概率的计算
4.数据抽象:概率的概念
生活中
收集数据
总结规律
生活经验
数学中
收集数据
总结规律
数学试验
估计
如何才能获得随机事件发生的可能性大小呢
探究新知
两人一组,每组重复投币10次,记录正面出现的次数.
投币试验
投币要求
(1)检查是否有正反两面一元均匀硬币;
(2)一本课本平放桌面上,一本课本卷起立在平放着的课本上;
(3)以书本的高度把硬币竖直从洞口抛下;
(4)一个同学抛,一个同学记录.
探究新知
1.以上试验中,正面朝上的次数叫做 ,事件A出现的次数
与总实验次数n的比例叫做事件A出现的 . 即 .
填写
频数
频率fn(A)
2. 必然事件的频率为 ,不可能事件的频率为 ,随机事件的
频率取值范围是 , 频率的取值范围是 .
1
0
(0,1)
3.试验结果与其他同学比较,你的结果和他们一致吗 为什么
因为“抛掷一枚硬币,正面朝上”这个事件是一个随机事件,在每一次试验中,它的结果是随机的,所以10次的试验结果也是随机的,频率可能会不同.
讨论
思考
[0,1]
探究新知
计算机模拟试验:
抛掷硬币试验
利用计算机模拟抛掷硬币,重复做大量的试验.观察频率有什么规律
“抛掷一枚硬币,正面朝上”的试验,每次试验的频率可能会不同,但随着试验次数的增加,正面朝上的频率逐渐稳定在0.5附近.
探究新知
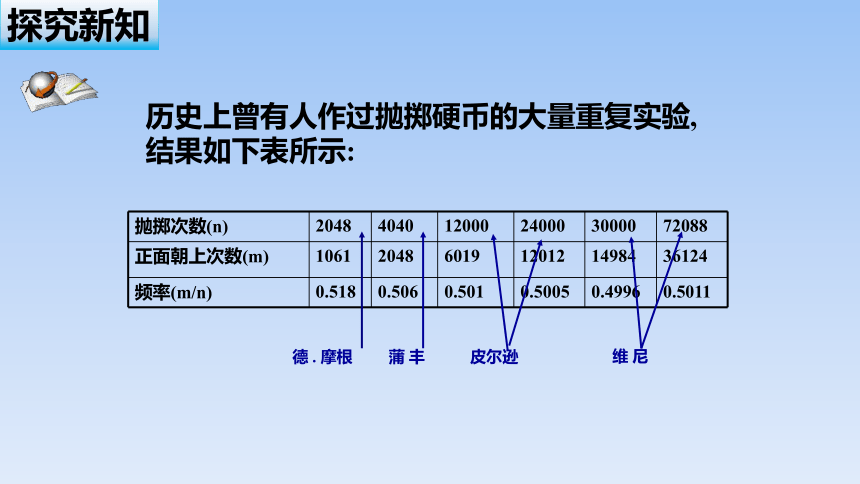
抛掷次数(n) 2048 4040 12000 24000 30000 72088
正面朝上次数(m) 1061 2048 6019 12012 14984 36124
频率(m/n) 0.518 0.506 0.501 0.5005 0.4996 0.5011
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示:
德 . 摩根
蒲 丰
皮尔逊
维 尼
探究新知
经过大量的重复试验,事件A发生的频率会逐渐稳定在区间[0,1]中的某个常数上.
用频率来估计概率
是一个确定的值
试 验 结 论:
这个常数就是事件A发生的概率.
随着试验次数的增加,频率稳定在0.5附近
总结:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐稳定在0.5附近.
探究新知
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在区间[0,1]中的某个常数上,把这个常数称为事件A的概率,记作P(A).
填一填
(1)概率的范围是 ,不可能事件的概率为 ,必然事件为 ,随机事件的概率 ;
[0,1]
0
1
(0,1)
思考 : 频率是否等同于概率呢
总结:概率从数量上反映了一个事件发生的可能性的大小.
(2)概率越接近于1,表明事件A发生的频率越 ,频数越 ,也就是它发生的可能性越 .
概率越接近于0,表明事件A发生的频率越 ,频数越 ,也就是它发生的可能性越 .
大
大
大
小
小
小
探究新知
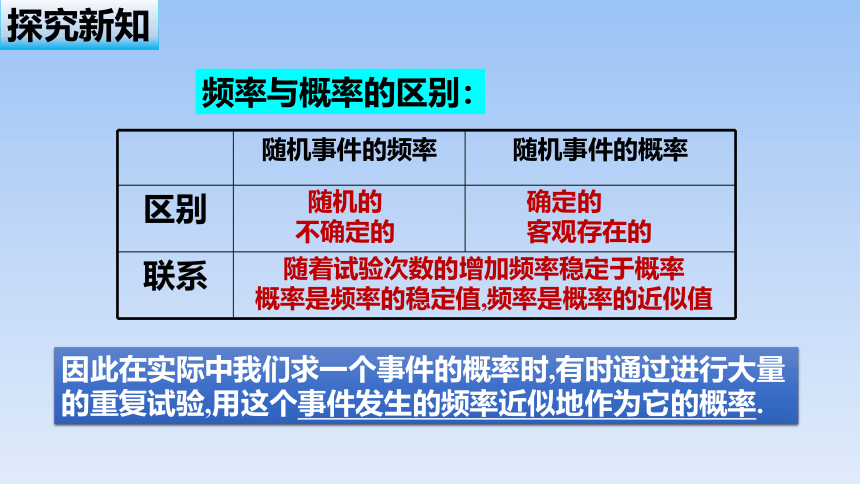
频率与概率的区别:
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
随机事件的频率 随机事件的概率
区别
联系
随机的
不确定的
确定的
客观存在的
随着试验次数的增加频率稳定于概率
概率是频率的稳定值,频率是概率的近似值
探究新知
探究新知
用频率估计概率,需要做大量的重复试验,有没有其他方法可以替代试验呢
我们知道,利用计算器或计算机软件可以产生随机数.
实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,这样就可以快速地进行大量重复试验了.
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0,1}的随机数,用0表示反面朝上,用1表示正面朝上.这样不断产生0,1两个随机数,相当于不断地做抛掷硬币的试验.
随机数的产生
应用计算器或计算机软件产生随机数时要特别注意遵照随机数产生的方法进行,切不可随意改变其步骤顺序和操作程序,否则会出现错误
(1)标号:把n个__________________相同的小球分别标上1,2,3,…,n.
(2)搅拌:放入一个袋中,把它们______________.
(3)摸取:从中摸出_______.
这个球上的数就称为从1~n之间的随机整数,简称随机数.
充分搅拌
一个
探究新知
伪随机数的产生
(1)规则:依照确定的算法.
(2)特点:具有周期性(周期很长).
(3)性质:它们具有类似_________的性质.
计算机或计算器产生的随机数并不是真正的随机数,我们称为____________.
随机数
伪随机数
大小、形状
产生随机数的常用方法
①_________________;②_____________________;③____________.
用计算器产生
用计算机产生
抽签法
探究新知
随机模拟方法(蒙特卡洛方法)
利用计算机或计算器产生的随机数来做模拟试验,通过模拟试验得到的_______来估计________,这种用计算机或计算器模拟试验的方法称为随机模拟方法或蒙特卡洛方法.
频 率
概 率
概率从数量上反映了一个事件发生的可能性的大小;
1、某篮球运动员在同一条件下的投篮结果如下:
投篮次数 8 10 15 20 30 40 50
进球次数 6 8 12 17 25 32 39
进球频率
思考1:若这位运动员进球的概率是0.8,那么他投10次篮一定能投中8次吗
0.78
0.75
0.80
0.80
0.85
0.83
0.80
这位运动员投篮一次,进球的概率约是多少
思考2:“若这位运动员进球的概率是0.8,那么他投10000次篮大概能投中8000次”,这种说法对吗
思考3:试验1000次得到的频率一定比试验的800次
得到的频率更接近概率吗
不对
对
不一定
0.8
典例讲解
1.某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
0.8
0.95
0.88
0.92
0.89
0.91
0.90
变式训练
典例讲解
例2、有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗 请说明理由.
解析
(1)记甲,乙摸出的数字为( x,y ) ,则共有4×4=16(种)情况,则x>y的有(4,1),(4,2),(4,3),(3,2),(3,1),(2,1),共6种情况,故甲获胜的概率为 =
典例讲解
例2、有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗 请说明理由
解析
(2)不公平.理由如下:摸到的球上所标数字相同的情况有(4,4),(3,3),(2,2),(1,1),共4种情况,故甲获胜的概率为 = ,乙获胜的概率 = ,故不公平.
方法归纳
概率在游戏中的运用
1.计算出各游戏者获胜的概率.
2.概率大的获胜的可能性大.
3.若各游戏者获胜的概率相同,即各人获胜的可能性相等,则游戏是公平的;否则就不公平.
变式训练
2. 转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍”或“不是4的整数倍”.
请回答下列问题:
(1)为了尽可能获胜,乙应怎么选
(2)为了保证游戏的公平性乙应选哪种猜数方案
解析
选A方案,无论乙猜“是奇数”或“是偶数”,乙获胜的概率都是0.5;选B方案,若乙猜“是4的整数倍”,则获胜的概率是= 0.2,若乙猜“不是4的整数倍”,则获胜的概率是= 0.8.
(1)0.8>0.5>0.2,为了尽可能获胜,乙应选择方案B,猜“不是4的整数倍”.
(2)为了保证游戏的公平性,应当选择方案A,方案A无论乙猜什么,乙获胜的概率都是0.5,甲获胜的概率也是0.5,两人获胜的概率相等,从而保证了该游戏的公平性.
变式训练
甲箱中有99个白球和1个黑球,故随机地取出1球,得白99球的可能性是;乙箱中有1个白球和99个黑球,从中任取1球,得到白球的可能性是,由此可知,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.根据极大似然法,可以认为白球是从概率大的箱子中抽出的.所以推断该白球是从甲箱中取出的.
例3、设有外形完全相同的2个箱子,甲箱有99个白球和1个黑球,乙箱有1个白球和99个黑球.现随机抽取1箱,再从该箱中抽取1球,结果取得白球.问:这球是从哪一个箱子中取出的
解析
典例讲解
解析
我们取三张卡片,上面分别标有1,2,3,抽到“1”就表示中签.假设抽签的次序为甲、乙、丙,则可以把所有的情况填入下表:
变式训练
3.元旦就要到了,某校欲举行联欢活动,每班派一人主持节目,高二(1)班的小明、小华和小丽实力相当,都争着要去,班主任决定用抽签的方式来决定,小强给小华出主意,要小华先抽,说先抽的机会大,你是怎么认为的
情况 人名 一 二 三 四 五 六
甲 1 1 2 2 3 3
乙 2 3 1 3 1 2
丙 3 2 3 1 2 1
从上表可以看出:甲、乙、丙依次抽签共有六种情况,第一、二种情况,甲中签第三、五种情况,乙中签;第四、六种情况,丙中签.由此可知,甲、乙、丙中签的可能性相同,即甲、乙、丙中签的机会是一样的,所以对于小华来说,先抽后抽,机会是均等的.
例4、天气预报说,在今后的三天中,每一天下雨的概率均为50%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率为( )
A.0.30 B.0.35 C.0.40 D.0.50
解析
根据题意可知,20组数据中表示三天中恰有两天下雨的有191,271,932,812,393,
027,730,共7组.根据随机模拟的方法可估计这三天中恰有两天下雨的概率为= 0.35.
故选B.
典例讲解
方法归纳
用随机模拟试验估计概率时,首先要确定随机数的范围和用哪些数代表不同的试验结果.当每次试验结果需要n个随机数表示时,要把n个随机数作为一组来处理,此时一定要注意每组中的随机数字能否重复.
4.甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.经随机模拟试验产生了如下30组随机数:
034 743 738 636 964 736 614 698
637 162 332 616 804 560 111 410
959 774 246 762 428 114 572 042
533 237 322 707 360 751
据此估计乙获胜的概率为 .
变式训练
如果6,7,8,9中恰有2个或3个数出现,就表示乙获胜,它们分别是738,636,964,736,698,637,616,959,774,762,707,共11个.所以采用三局两胜制,乙获胜的概率约为≈0.367.
解析
变式训练
当堂练习
1.某人将一枚质地均匀的硬币连掷了10次,6次正面朝上,若用A表示“正面朝上”这一事件,则A出现的( )
A.概率为 B.频率为 C.频率为6 D.概率为6
B
2.用随机模拟方法得到的频率( )
A.大于概率 B.小于概率 C.等于概率 D.是概率的近似值
D
3.某事件的概率是万分之一,说明了( )
A.概率太小,该事件几乎不可能发生 B.10000次中一定发生1次
C.10000人中,9999人说不发生,1人说发生 D.10000次中不可能发生10000次
A
4.掷两枚均匀的正方体骰子,用随机模拟方法估计出现点数之和为10的概率时产生的整数随机数中,每几个数为组( )
A. B. C. D.
B
5.采用随机模拟的方法估算某运动员射击击中目标的概率,先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为 .
当堂练习
归纳小结
频率与概率
频率的稳定性
随机模拟
频率与概率的理解
频率与概率的关系
概率的应用
作 业
P257 练习:1、2
即两个相互独立事件同时发生的概率,等于每个事件发生的概率的积.
2.推广:如果事件相互独立,那么这n个事件同时发生的概率等于每个事件发生的概率的积.即:
1.若是相互独立事件,则有
相互独立事件同时发生的概率公式
复习引入
人教A版同步教材名师课件
频率与概率
学习目标
学 习 目 标 核心素养
结合实例,会用频率估计概率 数学分析
了解随机模拟,会用随机模拟的方法估计事件的概率 数学运算
学习目标
课程目标:
1.通过实验让学生理解当试验次数较大时,实验频率稳定在某一常数附近,并据此
能估计出某一事件发生的频率.
2.通过对实际问题的分析,培养使用数学的良好意识,激发学习兴趣,体验数学的应用价值.
学科素养:
1.数学建模:概率的应用
2.逻辑推理:频率与概率的关系
3.数学运算:频率与概率的计算
4.数据抽象:概率的概念
生活中
收集数据
总结规律
生活经验
数学中
收集数据
总结规律
数学试验
估计
如何才能获得随机事件发生的可能性大小呢
探究新知
两人一组,每组重复投币10次,记录正面出现的次数.
投币试验
投币要求
(1)检查是否有正反两面一元均匀硬币;
(2)一本课本平放桌面上,一本课本卷起立在平放着的课本上;
(3)以书本的高度把硬币竖直从洞口抛下;
(4)一个同学抛,一个同学记录.
探究新知
1.以上试验中,正面朝上的次数叫做 ,事件A出现的次数
与总实验次数n的比例叫做事件A出现的 . 即 .
填写
频数
频率fn(A)
2. 必然事件的频率为 ,不可能事件的频率为 ,随机事件的
频率取值范围是 , 频率的取值范围是 .
1
0
(0,1)
3.试验结果与其他同学比较,你的结果和他们一致吗 为什么
因为“抛掷一枚硬币,正面朝上”这个事件是一个随机事件,在每一次试验中,它的结果是随机的,所以10次的试验结果也是随机的,频率可能会不同.
讨论
思考
[0,1]
探究新知
计算机模拟试验:
抛掷硬币试验
利用计算机模拟抛掷硬币,重复做大量的试验.观察频率有什么规律
“抛掷一枚硬币,正面朝上”的试验,每次试验的频率可能会不同,但随着试验次数的增加,正面朝上的频率逐渐稳定在0.5附近.
探究新知
抛掷次数(n) 2048 4040 12000 24000 30000 72088
正面朝上次数(m) 1061 2048 6019 12012 14984 36124
频率(m/n) 0.518 0.506 0.501 0.5005 0.4996 0.5011
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示:
德 . 摩根
蒲 丰
皮尔逊
维 尼
探究新知
经过大量的重复试验,事件A发生的频率会逐渐稳定在区间[0,1]中的某个常数上.
用频率来估计概率
是一个确定的值
试 验 结 论:
这个常数就是事件A发生的概率.
随着试验次数的增加,频率稳定在0.5附近
总结:“掷一枚硬币,正面朝上”在一次试验中是否发生不能确定,但随着试验次数的增加,正面朝上的频率逐渐稳定在0.5附近.
探究新知
对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在区间[0,1]中的某个常数上,把这个常数称为事件A的概率,记作P(A).
填一填
(1)概率的范围是 ,不可能事件的概率为 ,必然事件为 ,随机事件的概率 ;
[0,1]
0
1
(0,1)
思考 : 频率是否等同于概率呢
总结:概率从数量上反映了一个事件发生的可能性的大小.
(2)概率越接近于1,表明事件A发生的频率越 ,频数越 ,也就是它发生的可能性越 .
概率越接近于0,表明事件A发生的频率越 ,频数越 ,也就是它发生的可能性越 .
大
大
大
小
小
小
探究新知
频率与概率的区别:
因此在实际中我们求一个事件的概率时,有时通过进行大量的重复试验,用这个事件发生的频率近似地作为它的概率.
随机事件的频率 随机事件的概率
区别
联系
随机的
不确定的
确定的
客观存在的
随着试验次数的增加频率稳定于概率
概率是频率的稳定值,频率是概率的近似值
探究新知
探究新知
用频率估计概率,需要做大量的重复试验,有没有其他方法可以替代试验呢
我们知道,利用计算器或计算机软件可以产生随机数.
实际上,我们也可以根据不同的随机试验构建相应的随机数模拟试验,这样就可以快速地进行大量重复试验了.
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0,1}的随机数,用0表示反面朝上,用1表示正面朝上.这样不断产生0,1两个随机数,相当于不断地做抛掷硬币的试验.
随机数的产生
应用计算器或计算机软件产生随机数时要特别注意遵照随机数产生的方法进行,切不可随意改变其步骤顺序和操作程序,否则会出现错误
(1)标号:把n个__________________相同的小球分别标上1,2,3,…,n.
(2)搅拌:放入一个袋中,把它们______________.
(3)摸取:从中摸出_______.
这个球上的数就称为从1~n之间的随机整数,简称随机数.
充分搅拌
一个
探究新知
伪随机数的产生
(1)规则:依照确定的算法.
(2)特点:具有周期性(周期很长).
(3)性质:它们具有类似_________的性质.
计算机或计算器产生的随机数并不是真正的随机数,我们称为____________.
随机数
伪随机数
大小、形状
产生随机数的常用方法
①_________________;②_____________________;③____________.
用计算器产生
用计算机产生
抽签法
探究新知
随机模拟方法(蒙特卡洛方法)
利用计算机或计算器产生的随机数来做模拟试验,通过模拟试验得到的_______来估计________,这种用计算机或计算器模拟试验的方法称为随机模拟方法或蒙特卡洛方法.
频 率
概 率
概率从数量上反映了一个事件发生的可能性的大小;
1、某篮球运动员在同一条件下的投篮结果如下:
投篮次数 8 10 15 20 30 40 50
进球次数 6 8 12 17 25 32 39
进球频率
思考1:若这位运动员进球的概率是0.8,那么他投10次篮一定能投中8次吗
0.78
0.75
0.80
0.80
0.85
0.83
0.80
这位运动员投篮一次,进球的概率约是多少
思考2:“若这位运动员进球的概率是0.8,那么他投10000次篮大概能投中8000次”,这种说法对吗
思考3:试验1000次得到的频率一定比试验的800次
得到的频率更接近概率吗
不对
对
不一定
0.8
典例讲解
1.某射手在同一条件下进行射击,结果如下表所示:
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是多少
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率
0.8
0.95
0.88
0.92
0.89
0.91
0.90
变式训练
典例讲解
例2、有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗 请说明理由.
解析
(1)记甲,乙摸出的数字为( x,y ) ,则共有4×4=16(种)情况,则x>y的有(4,1),(4,2),(4,3),(3,2),(3,1),(2,1),共6种情况,故甲获胜的概率为 =
典例讲解
例2、有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗 请说明理由
解析
(2)不公平.理由如下:摸到的球上所标数字相同的情况有(4,4),(3,3),(2,2),(1,1),共4种情况,故甲获胜的概率为 = ,乙获胜的概率 = ,故不公平.
方法归纳
概率在游戏中的运用
1.计算出各游戏者获胜的概率.
2.概率大的获胜的可能性大.
3.若各游戏者获胜的概率相同,即各人获胜的可能性相等,则游戏是公平的;否则就不公平.
变式训练
2. 转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍”或“不是4的整数倍”.
请回答下列问题:
(1)为了尽可能获胜,乙应怎么选
(2)为了保证游戏的公平性乙应选哪种猜数方案
解析
选A方案,无论乙猜“是奇数”或“是偶数”,乙获胜的概率都是0.5;选B方案,若乙猜“是4的整数倍”,则获胜的概率是= 0.2,若乙猜“不是4的整数倍”,则获胜的概率是= 0.8.
(1)0.8>0.5>0.2,为了尽可能获胜,乙应选择方案B,猜“不是4的整数倍”.
(2)为了保证游戏的公平性,应当选择方案A,方案A无论乙猜什么,乙获胜的概率都是0.5,甲获胜的概率也是0.5,两人获胜的概率相等,从而保证了该游戏的公平性.
变式训练
甲箱中有99个白球和1个黑球,故随机地取出1球,得白99球的可能性是;乙箱中有1个白球和99个黑球,从中任取1球,得到白球的可能性是,由此可知,这一白球从甲箱中抽出的概率比从乙箱中抽出的概率大得多.根据极大似然法,可以认为白球是从概率大的箱子中抽出的.所以推断该白球是从甲箱中取出的.
例3、设有外形完全相同的2个箱子,甲箱有99个白球和1个黑球,乙箱有1个白球和99个黑球.现随机抽取1箱,再从该箱中抽取1球,结果取得白球.问:这球是从哪一个箱子中取出的
解析
典例讲解
解析
我们取三张卡片,上面分别标有1,2,3,抽到“1”就表示中签.假设抽签的次序为甲、乙、丙,则可以把所有的情况填入下表:
变式训练
3.元旦就要到了,某校欲举行联欢活动,每班派一人主持节目,高二(1)班的小明、小华和小丽实力相当,都争着要去,班主任决定用抽签的方式来决定,小强给小华出主意,要小华先抽,说先抽的机会大,你是怎么认为的
情况 人名 一 二 三 四 五 六
甲 1 1 2 2 3 3
乙 2 3 1 3 1 2
丙 3 2 3 1 2 1
从上表可以看出:甲、乙、丙依次抽签共有六种情况,第一、二种情况,甲中签第三、五种情况,乙中签;第四、六种情况,丙中签.由此可知,甲、乙、丙中签的可能性相同,即甲、乙、丙中签的机会是一样的,所以对于小华来说,先抽后抽,机会是均等的.
例4、天气预报说,在今后的三天中,每一天下雨的概率均为50%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率为( )
A.0.30 B.0.35 C.0.40 D.0.50
解析
根据题意可知,20组数据中表示三天中恰有两天下雨的有191,271,932,812,393,
027,730,共7组.根据随机模拟的方法可估计这三天中恰有两天下雨的概率为= 0.35.
故选B.
典例讲解
方法归纳
用随机模拟试验估计概率时,首先要确定随机数的范围和用哪些数代表不同的试验结果.当每次试验结果需要n个随机数表示时,要把n个随机数作为一组来处理,此时一定要注意每组中的随机数字能否重复.
4.甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.经随机模拟试验产生了如下30组随机数:
034 743 738 636 964 736 614 698
637 162 332 616 804 560 111 410
959 774 246 762 428 114 572 042
533 237 322 707 360 751
据此估计乙获胜的概率为 .
变式训练
如果6,7,8,9中恰有2个或3个数出现,就表示乙获胜,它们分别是738,636,964,736,698,637,616,959,774,762,707,共11个.所以采用三局两胜制,乙获胜的概率约为≈0.367.
解析
变式训练
当堂练习
1.某人将一枚质地均匀的硬币连掷了10次,6次正面朝上,若用A表示“正面朝上”这一事件,则A出现的( )
A.概率为 B.频率为 C.频率为6 D.概率为6
B
2.用随机模拟方法得到的频率( )
A.大于概率 B.小于概率 C.等于概率 D.是概率的近似值
D
3.某事件的概率是万分之一,说明了( )
A.概率太小,该事件几乎不可能发生 B.10000次中一定发生1次
C.10000人中,9999人说不发生,1人说发生 D.10000次中不可能发生10000次
A
4.掷两枚均匀的正方体骰子,用随机模拟方法估计出现点数之和为10的概率时产生的整数随机数中,每几个数为组( )
A. B. C. D.
B
5.采用随机模拟的方法估算某运动员射击击中目标的概率,先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为 .
当堂练习
归纳小结
频率与概率
频率的稳定性
随机模拟
频率与概率的理解
频率与概率的关系
概率的应用
作 业
P257 练习:1、2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
