数学归纳法
图片预览









文档简介
课件150张PPT。2.3.1
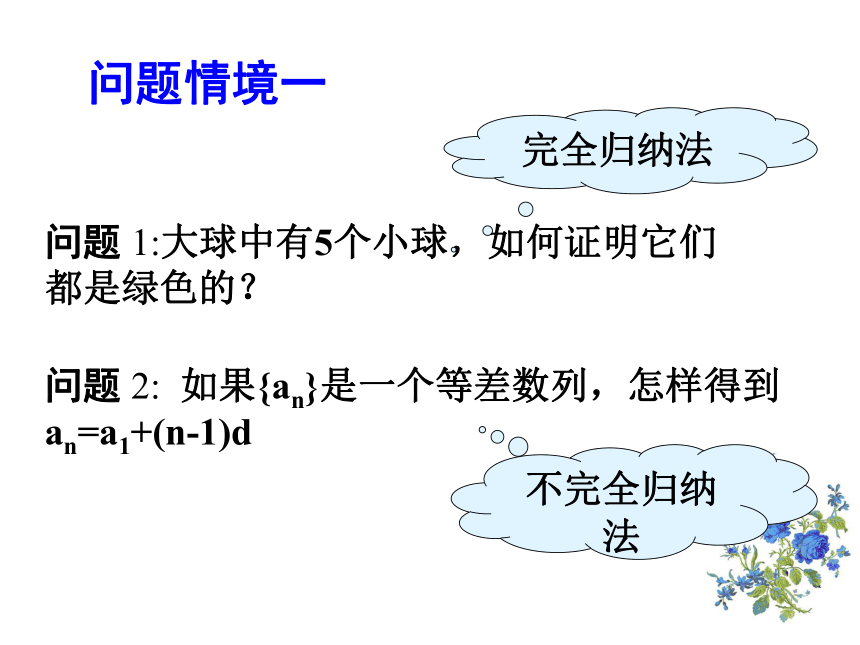
数学归纳法问题情境一问题 1:大球中有5个小球,如何证明它们都是绿色的? 问题 2: 如果{an}是一个等差数列,怎样得到 an=a1+(n-1)d 完全归纳法 不完全归纳法 :由一系列有限的特殊事例得出一般结论的推理方法 结论一定可靠结论不一定可靠考察全体对象,得到一般结论的推理方法考察部分对象,得到一般结论的推理方法归纳法分为完全归纳法 和 不完全归纳法归纳法问题情境二多
米
诺
骨
牌
课
件
演
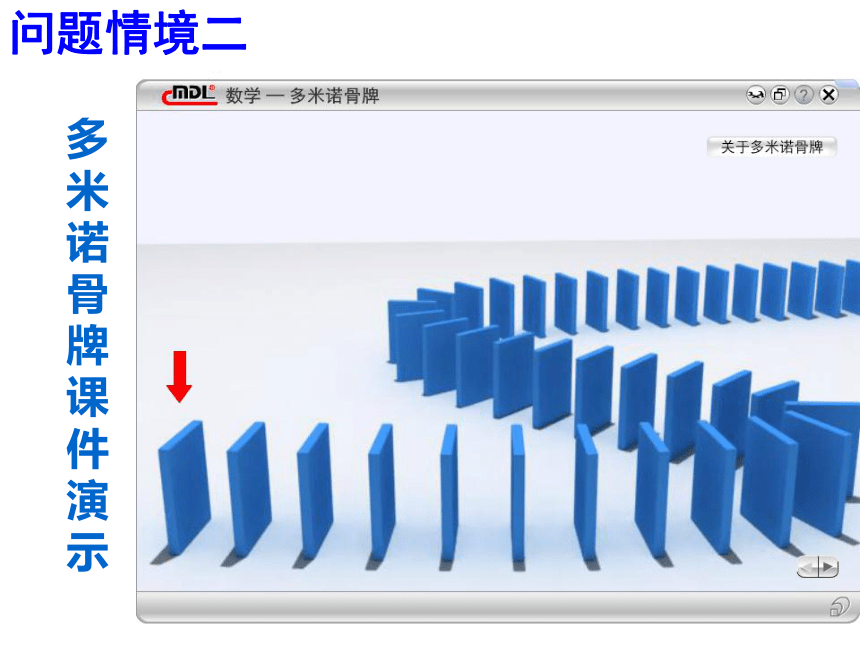
示 ?多米诺骨牌课件演示 如何保证骨牌一一倒下?需要哪些条件?(2)任意相邻的两块骨牌,若前一块倒下,则必须保证下一块要相继倒下。(1)第一块骨牌倒下----------递推关系;即第k块倒下,则相邻的第k+1块也倒下----------奠基;(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌) (1)处理第一个问题;(相当于推倒第一块骨牌)
问题情境三数学归纳法的概念: 定义:对于某些与正整数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0 (n0 ?N*)时命题成立 (归纳奠基) ;2.然后假设当n=k(k?N*,k≥n0)时命题成立,
证明当n=k+1时命题也成立(归纳递推)。
这种证明方法就叫做______________。数学归纳法已知数列{an}的第一项 a1=1, 且(n=1, 2,…), 试归纳出这个数列的通项公式.由此猜想:思考?证明:(1)当n=1时,猜想成立.(2)假设n=k时,猜想成立. 即那么,当n=k+1时即当 n=k+1时猜想也成立.所以对任何n?N*猜想都成立,即例. 已知数列 ,计算数列和
S1、S2、S3、S4,根据计算结果,猜想Sn的表达式,
并用数学归纳法进行证明. 证明:(1)当n=1时,左边=S1= ,右边= ,猜想成立.解析:猜想 .题型三 归纳、猜想、证明(2)假设当n=k(k∈N+)时猜想成立,即 则当n=k+1时, 所以,当n=k+1时,猜想成立,根据(1)(2)知猜想对任意n∈N+都成立. 1)明确首先取值n0并验证命题真假(必不可少);
2)“假设n=k时命题正确”并写出命题形式;
3)分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别,弄清左端应增加的项;
4)明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等;
5)两个步骤、一个结论缺一不可,否则结论不能成立:
递推基础不可少,归纳假设要用到,结论写明莫忘掉用数学归纳法证明恒等式的步骤及注意事项:(1)在第二步中,证明n=k+1命题成立时,必须用到
n=k命题成立这一归纳假设,否则就打破数学
归纳法步骤之间的逻辑严密关系,造成推理无
效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时
应根据具体情况而定.(3)在证明n=k+1命题成立用到n=k命题成立时,要
分析命题的结构特点,分析“n=k+1时”命题是什
么,并找出与“n=k”时命题形式的差别.弄清
应增加的项.∴n=1时等式成立。
②假设n=k时,命题成立,即那么,当n=k+1时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。问题情境一3.某个命题当n=k (k∈N )时成立,可证得当n=k+1时也成立。现在已知当n=5时该命题不成立,那么可推得( )
A. n=6时该命题不成立
B. n=6时该命题成立
C. n=4时该命题不成立
D. n=4时该命题成立C六、课后作业: 1、用数学归纳法证明: 在验证时,等式左边的项是( ) A、B、C、 D、C3、用数学归纳法证明不等式时的过程中,由到时,不等式的左边( )A、增加了一项B、增加了一项,又减少了一项C、增加了两项D、增加两项,又减少了一项D课堂练习2:课堂练习1:练习巩固 练习巩固 这就是说,当n=k+1时,命题也成立.没有用上“假设”,故此法不是数学归纳法请修改为数学归纳法证明 ①当n=1时,左边= , ②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,由 ①②知,对一切正整数n,原等式均正确. 这才是数学归纳法②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,这就是说,当n=k+1时,命题也成立.由 ①②知,对一切正整数n,原等式均正确.
证明:①当n=1时,左边=右边=②假设当n=k时,命题成立,即那么,当n=k+1时,有∴n=1时等式成立.即当 n=k+1时命题也成立.
由(1)和(2),可知原命题对任何n?N*都成立.[通一类][研一题]题型二 用数学归纳法证明不等式【例】求证: (n≥2,n∈N+).分析 和正整数有关,因此可用数学归纳法证明.证明(1)当n=2时,
左边 = ,不等式成立.(2)假设当n=k(k≥2,k∈N+)时不等式成立, 即 成立.则当n=k+1时,所以当n=k+1时不等式也成立. 由(1)(2)可知原不等式对一切n≥2,n∈N+都成立.放缩法2、用数学归纳法证明:1+时,由递推到时左边需添的项是( )D、 B、 C、A、D课堂练习3: D课堂练习2:?5用数学归纳法证明?+?+?+…+?<1-?(n≥2,n∈N*).证明:(1)当n=2时,左边=?=?,右边=1-?=?.因为?=11 (11k+2+122k+1)?11?122k+1+122?122k+1
= 11?11(11k+2+122k+1)+ 122k+1(144?11)
=11?(11k+2+122k+1)+ 122k+1?133.例3.证明:对任意正整数n,数11n+2+122n+1是133的倍数.证明:(1)当n=1时,11n+2+122n+1=113+123=23?133,
∴23?133能被133整除,即n=1时命题成立.那么11(k+1)+2+122(k+1)+1(3)整除性问题由归纳假设知11k+2+122k+1及122k+1?133都能被133整除,
∴11(k+1)+2+122(k+1)+1能被133整除,
即n=k+1时命题也成立.例3.证明:对任意自然数n,数11n+2+122n+1是133的倍数.(3)整除性问题证明:根据(1)和(2),可知命题对任何n?N﹡都成立.探究平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一点,证明:它们的交点的个数为f(n)= .证明:(1)当n=2时,两条直线的交点只有一个,
又f(2)= ×2×(2-1)=1,
因此,当n=2时,命题成立.
(2)假设当n=k(k≥2,k∈N*)时命题成立,就是说,平面内满足题设的任何k条直线的交点的个数f(k)= k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l(如下图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)= k(k-1).另外,因为已知任何两条直线不平行,所以直线l必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不相同,且与平面内其他的 k·(k-1)个交点也两两不相同,从而平面内交点的个数是 k(k-1)+k= k[(k-1)+2]= (k+1)[(k+1)-1].
这就是说,当n=k+1时,k+1条直线的交点个数为
f(k+1)= (k+1)[(k+1)-1].
根据(1)、(2)可知命题对任何大于2的正整数都成立.【例题3】 有n个圆,其中每两个圆相交于两点,并且每三个圆都不 相交于同一点,求证:这n个圆把平面分成f(n)=n2-n+2部分.分析:解答本题的关键是在第二步中如何正确地应用假设.证明:(1)当n=1时,分为两部分,f(1)=2,命题成立;(2)假设n=k(k≥1,k∈N*)时,被分成f(k)=k2-k+2部分;那么当n=k+1时,依题意,第k+1个圆与前k个圆产生2k个交点,第k+1 个圆被截为2k段弧,每段弧把所经过的区域分为两部分,∴平面上增加了2k个区域.∴f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2,即n=k+1时命题成立,由(1)(2)知命题成立.框图表示命题有成立的情况命题能连续成立归纳奠基归纳递推例:如下证明对吗?证明:①当n=1时,左边= 右边= 等式成立。
②设n=k时,有那么,当n=k+1时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。第二步证明中没有用到假设,这不是数学归纳法证明。(1)在第二步中,证明n=k+1命题成立时,必须用到n=k命题成立这一归纳假设,否则就打破数学归纳法步骤之间的逻辑严密关系,造成推理无效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时应根据具体情况而定.例:欲用数学归纳法证明2n>n2,试问n的第一个取值应是多少?答:对n=1,2,3,…,逐一尝试,可知初始值为n=5.证明 ①当n=1时,左边=1 =右边,等式显然成立。例 证明:递推基础递推依据②假设当n=k时等式成立,即那么,当n=k+1时,有这就是说,当n=k+1时,等式也成立。根据①和②,可知对任何n?N*等式都成立。那么当n=k+1时,这就是说,当n=k+1时,等式也成立练习1 用数学归纳法证明:递推基础递推依据用数学归纳法证明与正整数有关命题的步骤是:递推基础递推依据“找准起点,奠基要稳”“用上假设,递推才真”“综合(1)、(2),……”不可少!注意:数学归纳法使用要点: 两步骤,一结论。注意 :1、用数学归纳法进行证明时,要分两个步骤,两步同样重要,两步骤缺一不可.2、第二步证明,由假设n=k时命题成立,到n=k+1时.必须用假设条件,否则不是数学归纳法。3、最后一定要写“由(1)(2)……”1.用数学归纳法证明等式 1+2+3+…(2n+1)=(n+1)(2n+1)时,
当n=1时,左边所得项是 ;
当n=2时,左边所得项是 ;1+2+31+2+3+4+5A、1B、1+aC、1+a+a2D、1+a+a2+a3C课堂练习:3、 用数学归纳法证明 证明(1)当n=1时,左边=1,右边=1,等式成立.这就是说,当n=k+1时,等式也成立.由(1)和(2),可知等式对任何正整数n都成立.(2)假设当n=k时,等式成立,即递推基础递推依据那么当n=k+1时,例、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)三、巩固练习:
1.用数学归纳法证明:“ ” 在验证n=1成立时,左边计算所得的结果是 .
2.已知:,则 等于
3.用数学归纳法证明:1×2+2×3+3×4+……+n(n+1)
=练习巩固 1.已知: ,则 等于( )
A:
B:
C:
D: C练习回顾(1)当n=1时,由上面解法知结论正确.(1)数学归纳法证明等式问题:二、数学归纳法应用举例:则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.则当n=k+1时,故当n=k+1时,结论也成立.根据(1)、(2)知,对一切正整数n,结论都成立.(2)数学归纳法证明整除问题:例1、用数学归纳法证明:
当n为正偶数时,xn-yn能被x+y整除.证:(1)当n=2时,x2-y2=(x+y)(x-y),即能被x+y整除,故命
题成立.(2)假设当n=2k时,命题成立,即x2k-y2k能被x+y整除.故x2k+2-y2k+2能被x+y整除,即当n=2k+2时命题成立.由(1)、(2)知原命题对一切正偶数均成立.证:(1)当n=1时,A1=5+2+1=8,命题显然成立.因为Ak是8的倍数,3k-1+1是偶数即4(3k-1+1)也是
8的倍数,所以Ak+1也是8的倍数,即当n=k+1时,命题成立.由(1)、(2)知对一切正整数n, An能被8整除.例3、求证:x3n-1+x3n-2+1能被x2+x+1整除.证:(1)当n=1时, x3n-1+x3n-2+1= x2+x+1,从而命题成立.(2)假设当n=k时命题成立,即x3k-1+x3k-2+1能被
x2+x+1整除则当n=k+1时,x3(k+1)-1+x3(k+1)-2+1=x3k+2+x3k+1+1=x3(x3k-1+x3k-2+1)+x3+1
= x3(x3k-1+x3k-2+1)+(x+1)(x2+x+1)因为x3k-1+x3k-2+1、x2+x+1都能被x2+x+1整除,所以上式右边能被x2+x+1整除.即当n=k+1时,命题成立.根据(1)、(2)知,对一切正整数n,命题成立.当n=k+1时:第k+1条直线分别与前k条直线各交于
一点,共增加k个点,由1)、2)可知,对一切n∈N?原命题均成立。(3)数学归纳法证明几何问题:练习1:凸n边形有f(n)条对角线,则凸n+1边形的对角线
的条数f(n+1)=f(n)+_________.n-1练习2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.2k(4)数学归纳法证明不等式问题:则当n=k+1时,我们有:即当n=k+1时,不等式也成立.证:(1)当n=1时,左边=1,右边=2, 不等式显然成立.则当n=k+1时,我们有:即当n=k+1时,不等式也成立.根据(1)、(2)可知,原不等式对一切正整数都 成立.即当n=k+1时,命题成立.例4、已知x> ?1,且x?0,n?N,n?2.
求证:(1+x)n>1+nx.(2)假设n=k时,不等式成立,即 (1+x)k>1+kx
当n=k+1时,因为x> ?1 ,所以1+x>0,于是
左边=(1+x)k+1=(1+x)k(1+x)>(1+x)(1+kx)=1+(k+1)x+kx2;
右边=1+(k+1)x.
因为kx2>0,所以左边>右边,即(1+x)k+1>1+(k+1)x.
这就是说,原不等式当n=k+1时也成立.
根据(1)和(2),原不等式对任何不小于2的自然数n都成立.证明: (1)当n=2时,左=(1+x)2=1+2x+x2
∵ x?0,∴ 1+2x+x2>1+2x=右
∴n=1时不等式成立则当n=k+1时, 有:即当n=k+1时,不等式成立. 五、小结:1.与正整数有关的数学命题可以考虑用数学归纳法证
明,但注意不要滥用.要掌握数学归纳法的实质与步
步. 2.归纳思想充分体现了辩证唯物主义的特殊与一般的
辨证思想,是数学的基本思想,数学归纳法体现了有
限辨证关系与转化的思想.3. 数学归纳法的应用通常与数学的其他方法联系在一
起的,如比较法、放缩法、配凑法、分析法和综合法
等. 数学归纳法的第一步是递推的基础,有了此基础,在
第二步中的假设才能成立,才不是真正意义上的纯粹假设. 第二步是递推的依据,当假设中的某些情况(n≥n0)
时n取值较小的情况)成为事实后,依据第二步就可知当n取下一个值时命题也成立,如此又增加了假设中变为命题成立的n的取值,经不断地循环递推便得到对满足n≥n0的所有正整数命题都成立.(1)重点:两个步骤、一个结论;注意:递推基础不可少,归纳假设要用到,结论写明莫忘掉。点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n 当n=4时,2n=16,n2=16, 2n=n2
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=n(n-1)/2.说明:用数学归纳法证明几何问题,重难点是处理好当n=k+1时利用假设结合几何知识证明命题成立.注:在上例的题设条件下还可以有如下二个结论:(1)设这n条直线互相分割成f(n)条线段或射线,
---则: f(n)=n2.(2)这n条直线把平面分成(n2+n+2)/2个区域.1:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,
证明这n条直线把平面分成f(n)=(n2+n+2)/2个区域.作业1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.思考题小结:
重点:两个步骤、一个结论;
注意:奠基基础不可少,
归纳假设要用到,
结论写明莫忘掉.一、复习回顾:什么是数学归纳法? 对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:(1)证明当n取第一个值n0(例如n0=1) 时命题成立;【归纳奠基】
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立
证明当n=k+1时命题也成立.
这种证明方法叫做 数学归纳法.数学归纳法【归纳递推】框图表示验证n=n0时命题成立若n=k(k≥n0)时命题成立,
证明n=k+1时命题也成立.归纳奠基归纳推理命题对从n0开始所有的正整数n都成立(1) 第一步,是否可省略? 不可以省略.(2)第二步,从n=k(k≥n0)时命题成立的假设出发,推证 n=k+1 时命题也成立.既然是假设,为什么还要把它当成条件呢?这一步是在第一步的正确性的基础上,证明传递性.想一想(1)当n=1,2,3,4时,计算f(n)的值.(2)你对f(n)的值有何猜想?用数学归纳法证明你的猜想.解:当n=1时, f(1) =51+2×31-1+1=8×1. 当n=2时, f(2) =52+2×32-1+1=8×4. 当n=3时, f(3) =53+2×33-1+1=8×18. 当n=4时, f(4) =54+2×34-1+1=8×35.例1 设n∈N*,5n+2×3n-1+1.证明 ①当n=1时,有f(1) =51+2×31-1+1=8能被8整除,命题成立.猜想:当n∈N*时, f(n) =5n+2×3n-1+1.能被8整除.②假设当n=k时命题成立,即f(k)能被8整除,那么当n=k+1时,有
f(k+1) =5k+1+2×3k+1-1+1
=5×5k+6×3k-1+1
=5×5k+2×3k-1+1+ 4(5k+3k-1)
= f(k)+4(5k+3k-1) 这里,5k和3k-1均为奇数,它们和(5k+3k-1)必为偶数,从而4(5k+3k-1)能被8整除.
由归纳假设,f(k)能被8整除,所以f(k+1)能被8整除,这就是说当n=k+1时命题也成立.
根据(1)(2),可知命题对于任意自然数都成立. 特别提示:
数学归纳法证题的关键是“一凑假设,二凑结论”,在证题的过程中,归纳推理一定要起到条件的作用,即证明n=k+1成立时必须用到归纳递推这一条件.(2)假设当n=k(k∈N+)时,命题成立,即有 ,当n=k+1时,当k+1条直线与前面k条直线有k个不同交点,即它被前面k条直线截成k+1段,其中每一段都把它所在的原区域一分为二,也即使原区域数目增加k+1.例2:平面上有n条直线,其中任意两条都相交,任意三条不共点,这些直线把平面分成多少个区域?
证明你的结论.解:这样的n条直线把平面分成的区域数目为 ,下面用数学归纳法证明: (1)当n=1时,一条直线将平面分成两部分,f(1)=2,∴n=1时,命题成立. 故当n=k+1时,命题成立.
由(1)(2)可知,对任意正整数n,命题成立.补充练习 有n个圆,其中每两个圆都相交于两点,并且每
三个圆都不相交于同一点,求证:这n个圆把平面分
成f(n)=n2-n+2个部分.证明:(1)当n=1时,即一个圆把平面分成二个部分, f(1)=2,又n=1时, n2-n+2=2,
∴命题成立.(2)假设当n=k时,命题成立,即k个圆把平面分成f(k)=k2-k+2个部分,那么由题意知第 k+1个圆与前k个圆中,每个圆交于两点,有无三圆交于同一点,于是它与其它k交于2k个点,把它分成2k条弧而每条弧把原区域分成2块,因此这个平面的总区域增加2k块,即f(k+1)=k2-k+2+2k=(k+1)2-(k+1)+2,即当n=k+1时,命题成立.
由(1)(2)可知,对任意的n∈N+,命题成立.1.用数学归纳法证明:1+2+22+…+2n-1=2n-1 (n∈N*).证明:(1)当n=1时,左边=1,右边=1,等式是成立的.
(2)假设当n=k时等式成立,就是
1+2+22+…+2k-1 =2k-1
那么, 1+2+22+…+2k-1 +2k=2k-1 + 2k
=2×2k-1
=2k+1-1
这就是说,当n=k+1时,等式也成立. 因此,根据(1)和(2)可断定,等式对于任何n∈N*都成立.练习3.求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1).用数学归纳法证明恒等式的步骤及注意事项:① 明确首取值n0并验证真假.(必不可少)
②“假设n=k时命题正确”并写出命题形式.
③分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别.弄清左端应增加的项.
④ 明确等式左端变形目标,掌握恒等式变形常用的
方法:乘法公式、因式分解、添拆项、配方等,
并用上假设.(1)证明当n取第一个值n0(如 n0=1或2等)时结论正确 数学归纳法是一种证明与正整数有关的数学命题的重要方法.主要有两个步骤一个结论: 【归纳奠基】.(2)假设n=k时结论正确,证明n=k+1时结论也正确(3)由(1),(2)得出结论.【归纳递推】.(1)2+4+6+8+…+2n=n2+n+1(n?N*)证明 :假设当n=k时等式成立,即
2+4+6+8+…+2k=k2+k+1(k?N*)那么,当n=k+1时,有
2+4+6+8+…+2k+2(k+1)
=k2+k+1+2(k+1)
=(k+1)2+(k+1)+1 ,
因此,对于任何n?N*等式都成立。缺乏“递推基础”事实上,我们可以用等差数列求和公式验证原等式是不成立的!
(3)(纠错题)课本P87 T3 2n>n2(n?N*)证明 :①当n=1时,21>12,不等式显然成立。
②假设当n=k时等式成立,即2k>k2,
那么当n=k+1时,有
2k+1=2?2k=2k+2k>k2+k2?k2+2k+1=(k+1)2.
这就是说,当n=k+1时不等式也成立。
根据(1)和(2),可知对任何n?N*不等式都成立。虽然既有“递推基础”,又用到假设(“递推依据”),但在证明过程中出现错误,故上述证法错误!事实上,原不等式不成立,如n=2时不等式就不成立。练习巩固 CC练习巩固 练习巩固 提什么
好呢?
注意结论的形式 练习巩固 5.求证:当n∈N*时,证明: 练习巩固 1.用数学归纳法证明:
在验证 n=1成立时,左边计算所得的结果是( ) A.1 B.
C. D. C例1、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)(一)用数学归纳法证明等式或不等式(2)假设当n=k(k≥2)时不等式成立,即有: 则当n=k+1时,我们有:即当n=k+1时,不等式也成立.例2.用数学归纳法证明:例3:利用数学归纳法证明不等式
(n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时,不等式左边的变化是( ):练习(1)用数学归纳法证: D(2)用数学归纳法证: (n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时,左式所需添加的项数为( ):A.1项B. 项D. 项C. 项C(二)用数学归纳法证明整除问题(三)数学归纳法证明几何问题. 例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明这n条直线把平面分成f(n)=(n2+n+2)/2个部分.1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.练习(四)归纳—猜想—证明(求数列的 通项公式)(五)用数学归纳法证明探究性问题点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n 当n=4时,2n=16,n2=16, 2n=n2
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
证明:(1)当 时,不等式 显然成立 用数学归纳法证明: (2)假设 时不等式成立,即
那么,当 时,有 即当 时不等式也成立. 根据(1)(2),可知对任何 ,不等式都成立. [研一题][悟一法] 用数学归纳法证明与正整数有关的等式时,关键在于“看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与n的取值是否有关,由n=k到n=k+1时,等式两边会增加哪些项.[研一题][悟一法]
用数学归纳法证明不等式时要注意两凑:一凑归纳假设;二凑证明目标,在凑证明目标时,比较法、综合法、分析法都可选用.[通一类][研一题][悟一法]
解决此类问题的基本思路是:可以先从观察入手,发现问题的特点,以形成解决问题的初步思路,然后用归纳的方法进行试探,提出猜想,最后用数学归纳法给出证明.[通一类]3.已知数列{an}中,Sn是{an}的前n项和,且Sn是2a与-
2nan的等差中项,其中a是不等于零的常数.
(1)求a1,a2,a3;
(2)猜想an的表达式,并用数学归纳法加以证明.[悟一法]
(1)用数学归纳法证明几何命题时一要注意数形结合,二要注意有必要的文字说明.
(2)证明几何问题的关键是由n=k到n=k+1时f(n)的增加量,解题时可先用f(k+1)-f(k)得出结果,再结合图形给予说明.[通一类]4.平面内有n(n∈N*)个圆,其中每两个圆都相交于两点,
且每三个圆都不相交于同一点,求证:这n个圆把平面分成n2-n+2部分.
证明:(1)当n=1时,n2-n+2=2,即一个圆把平面分成两部分,故结论成立.
(2)假设当n=k(k≥1,k∈N*)时命题成立,即k个圆把平面分成k2-k+2部分.则当n=k+1时,这k+1个圆中的k个圆把平面分成k2-k+2个部分,第k+1个圆被前k个圆分成2k条弧,这2k条弧中的每一条把它所在的平面部分都分成两部分,这样共增加2k个部分,故k+1个圆把平面分成k2-k+2+2k=(k+1)2-(k+1)+2部分,即n=k+1时命题也成立.
综上所述,对一切n∈N*,命题都成立. [错因] 错解在证明当n=k+1等式成立时,没有用到归纳假设“当n=k(k∈N*)时等式成立”,故不符合数学归纳法证题的要求.(2)数学归纳法证题的步骤:两个步骤,一个结论; (3)数学归纳法优点:即克服了完全归纳法的繁杂的缺
点,又克服了不完全归纳法结论不可靠的不足。(4)数学归纳法的基本思想:运用“有限”的手段来
解决“无限”的问题(1)数学归纳法是一种证明与正整数有关的数学命题
的重要方法回顾反思
米
诺
骨
牌
课
件
演
示 ?多米诺骨牌课件演示 如何保证骨牌一一倒下?需要哪些条件?(2)任意相邻的两块骨牌,若前一块倒下,则必须保证下一块要相继倒下。(1)第一块骨牌倒下----------递推关系;即第k块倒下,则相邻的第k+1块也倒下----------奠基;(2)验证前一问题与后一问题有递推关系;
(相当于前牌推倒后牌) (1)处理第一个问题;(相当于推倒第一块骨牌)
问题情境三数学归纳法的概念: 定义:对于某些与正整数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0 (n0 ?N*)时命题成立 (归纳奠基) ;2.然后假设当n=k(k?N*,k≥n0)时命题成立,
证明当n=k+1时命题也成立(归纳递推)。
这种证明方法就叫做______________。数学归纳法已知数列{an}的第一项 a1=1, 且(n=1, 2,…), 试归纳出这个数列的通项公式.由此猜想:思考?证明:(1)当n=1时,猜想成立.(2)假设n=k时,猜想成立. 即那么,当n=k+1时即当 n=k+1时猜想也成立.所以对任何n?N*猜想都成立,即例. 已知数列 ,计算数列和
S1、S2、S3、S4,根据计算结果,猜想Sn的表达式,
并用数学归纳法进行证明. 证明:(1)当n=1时,左边=S1= ,右边= ,猜想成立.解析:猜想 .题型三 归纳、猜想、证明(2)假设当n=k(k∈N+)时猜想成立,即 则当n=k+1时, 所以,当n=k+1时,猜想成立,根据(1)(2)知猜想对任意n∈N+都成立. 1)明确首先取值n0并验证命题真假(必不可少);
2)“假设n=k时命题正确”并写出命题形式;
3)分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别,弄清左端应增加的项;
4)明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等;
5)两个步骤、一个结论缺一不可,否则结论不能成立:
递推基础不可少,归纳假设要用到,结论写明莫忘掉用数学归纳法证明恒等式的步骤及注意事项:(1)在第二步中,证明n=k+1命题成立时,必须用到
n=k命题成立这一归纳假设,否则就打破数学
归纳法步骤之间的逻辑严密关系,造成推理无
效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时
应根据具体情况而定.(3)在证明n=k+1命题成立用到n=k命题成立时,要
分析命题的结构特点,分析“n=k+1时”命题是什
么,并找出与“n=k”时命题形式的差别.弄清
应增加的项.∴n=1时等式成立。
②假设n=k时,命题成立,即那么,当n=k+1时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。问题情境一3.某个命题当n=k (k∈N )时成立,可证得当n=k+1时也成立。现在已知当n=5时该命题不成立,那么可推得( )
A. n=6时该命题不成立
B. n=6时该命题成立
C. n=4时该命题不成立
D. n=4时该命题成立C六、课后作业: 1、用数学归纳法证明: 在验证时,等式左边的项是( ) A、B、C、 D、C3、用数学归纳法证明不等式时的过程中,由到时,不等式的左边( )A、增加了一项B、增加了一项,又减少了一项C、增加了两项D、增加两项,又减少了一项D课堂练习2:课堂练习1:练习巩固 练习巩固 这就是说,当n=k+1时,命题也成立.没有用上“假设”,故此法不是数学归纳法请修改为数学归纳法证明 ①当n=1时,左边= , ②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,由 ①②知,对一切正整数n,原等式均正确. 这才是数学归纳法②假设n=k(k∈N*)时原等式成立 ,即此时,原等式成立。 那么n=k+1时,这就是说,当n=k+1时,命题也成立.由 ①②知,对一切正整数n,原等式均正确.
证明:①当n=1时,左边=右边=②假设当n=k时,命题成立,即那么,当n=k+1时,有∴n=1时等式成立.即当 n=k+1时命题也成立.
由(1)和(2),可知原命题对任何n?N*都成立.[通一类][研一题]题型二 用数学归纳法证明不等式【例】求证: (n≥2,n∈N+).分析 和正整数有关,因此可用数学归纳法证明.证明(1)当n=2时,
左边 = ,不等式成立.(2)假设当n=k(k≥2,k∈N+)时不等式成立, 即 成立.则当n=k+1时,所以当n=k+1时不等式也成立. 由(1)(2)可知原不等式对一切n≥2,n∈N+都成立.放缩法2、用数学归纳法证明:1+时,由递推到时左边需添的项是( )D、 B、 C、A、D课堂练习3: D课堂练习2:?5用数学归纳法证明?+?+?+…+?<1-?(n≥2,n∈N*).证明:(1)当n=2时,左边=?=?,右边=1-?=?.因为?=11 (11k+2+122k+1)?11?122k+1+122?122k+1
= 11?11(11k+2+122k+1)+ 122k+1(144?11)
=11?(11k+2+122k+1)+ 122k+1?133.例3.证明:对任意正整数n,数11n+2+122n+1是133的倍数.证明:(1)当n=1时,11n+2+122n+1=113+123=23?133,
∴23?133能被133整除,即n=1时命题成立.那么11(k+1)+2+122(k+1)+1(3)整除性问题由归纳假设知11k+2+122k+1及122k+1?133都能被133整除,
∴11(k+1)+2+122(k+1)+1能被133整除,
即n=k+1时命题也成立.例3.证明:对任意自然数n,数11n+2+122n+1是133的倍数.(3)整除性问题证明:根据(1)和(2),可知命题对任何n?N﹡都成立.探究平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一点,证明:它们的交点的个数为f(n)= .证明:(1)当n=2时,两条直线的交点只有一个,
又f(2)= ×2×(2-1)=1,
因此,当n=2时,命题成立.
(2)假设当n=k(k≥2,k∈N*)时命题成立,就是说,平面内满足题设的任何k条直线的交点的个数f(k)= k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l(如下图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)= k(k-1).另外,因为已知任何两条直线不平行,所以直线l必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不相同,且与平面内其他的 k·(k-1)个交点也两两不相同,从而平面内交点的个数是 k(k-1)+k= k[(k-1)+2]= (k+1)[(k+1)-1].
这就是说,当n=k+1时,k+1条直线的交点个数为
f(k+1)= (k+1)[(k+1)-1].
根据(1)、(2)可知命题对任何大于2的正整数都成立.【例题3】 有n个圆,其中每两个圆相交于两点,并且每三个圆都不 相交于同一点,求证:这n个圆把平面分成f(n)=n2-n+2部分.分析:解答本题的关键是在第二步中如何正确地应用假设.证明:(1)当n=1时,分为两部分,f(1)=2,命题成立;(2)假设n=k(k≥1,k∈N*)时,被分成f(k)=k2-k+2部分;那么当n=k+1时,依题意,第k+1个圆与前k个圆产生2k个交点,第k+1 个圆被截为2k段弧,每段弧把所经过的区域分为两部分,∴平面上增加了2k个区域.∴f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2,即n=k+1时命题成立,由(1)(2)知命题成立.框图表示命题有成立的情况命题能连续成立归纳奠基归纳递推例:如下证明对吗?证明:①当n=1时,左边= 右边= 等式成立。
②设n=k时,有那么,当n=k+1时,有即n=k+1时,命题成立。
根据①②问可知,对n∈N*,等式成立。第二步证明中没有用到假设,这不是数学归纳法证明。(1)在第二步中,证明n=k+1命题成立时,必须用到n=k命题成立这一归纳假设,否则就打破数学归纳法步骤之间的逻辑严密关系,造成推理无效. 证明中的几个注意问题:(2)在第一步中的初始值不一定从1取起,证明时应根据具体情况而定.例:欲用数学归纳法证明2n>n2,试问n的第一个取值应是多少?答:对n=1,2,3,…,逐一尝试,可知初始值为n=5.证明 ①当n=1时,左边=1 =右边,等式显然成立。例 证明:递推基础递推依据②假设当n=k时等式成立,即那么,当n=k+1时,有这就是说,当n=k+1时,等式也成立。根据①和②,可知对任何n?N*等式都成立。那么当n=k+1时,这就是说,当n=k+1时,等式也成立练习1 用数学归纳法证明:递推基础递推依据用数学归纳法证明与正整数有关命题的步骤是:递推基础递推依据“找准起点,奠基要稳”“用上假设,递推才真”“综合(1)、(2),……”不可少!注意:数学归纳法使用要点: 两步骤,一结论。注意 :1、用数学归纳法进行证明时,要分两个步骤,两步同样重要,两步骤缺一不可.2、第二步证明,由假设n=k时命题成立,到n=k+1时.必须用假设条件,否则不是数学归纳法。3、最后一定要写“由(1)(2)……”1.用数学归纳法证明等式 1+2+3+…(2n+1)=(n+1)(2n+1)时,
当n=1时,左边所得项是 ;
当n=2时,左边所得项是 ;1+2+31+2+3+4+5A、1B、1+aC、1+a+a2D、1+a+a2+a3C课堂练习:3、 用数学归纳法证明 证明(1)当n=1时,左边=1,右边=1,等式成立.这就是说,当n=k+1时,等式也成立.由(1)和(2),可知等式对任何正整数n都成立.(2)假设当n=k时,等式成立,即递推基础递推依据那么当n=k+1时,例、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)三、巩固练习:
1.用数学归纳法证明:“ ” 在验证n=1成立时,左边计算所得的结果是 .
2.已知:,则 等于
3.用数学归纳法证明:1×2+2×3+3×4+……+n(n+1)
=练习巩固 1.已知: ,则 等于( )
A:
B:
C:
D: C练习回顾(1)当n=1时,由上面解法知结论正确.(1)数学归纳法证明等式问题:二、数学归纳法应用举例:则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.则当n=k+1时,故当n=k+1时,结论也成立.根据(1)、(2)知,对一切正整数n,结论都成立.(2)数学归纳法证明整除问题:例1、用数学归纳法证明:
当n为正偶数时,xn-yn能被x+y整除.证:(1)当n=2时,x2-y2=(x+y)(x-y),即能被x+y整除,故命
题成立.(2)假设当n=2k时,命题成立,即x2k-y2k能被x+y整除.故x2k+2-y2k+2能被x+y整除,即当n=2k+2时命题成立.由(1)、(2)知原命题对一切正偶数均成立.证:(1)当n=1时,A1=5+2+1=8,命题显然成立.因为Ak是8的倍数,3k-1+1是偶数即4(3k-1+1)也是
8的倍数,所以Ak+1也是8的倍数,即当n=k+1时,命题成立.由(1)、(2)知对一切正整数n, An能被8整除.例3、求证:x3n-1+x3n-2+1能被x2+x+1整除.证:(1)当n=1时, x3n-1+x3n-2+1= x2+x+1,从而命题成立.(2)假设当n=k时命题成立,即x3k-1+x3k-2+1能被
x2+x+1整除则当n=k+1时,x3(k+1)-1+x3(k+1)-2+1=x3k+2+x3k+1+1=x3(x3k-1+x3k-2+1)+x3+1
= x3(x3k-1+x3k-2+1)+(x+1)(x2+x+1)因为x3k-1+x3k-2+1、x2+x+1都能被x2+x+1整除,所以上式右边能被x2+x+1整除.即当n=k+1时,命题成立.根据(1)、(2)知,对一切正整数n,命题成立.当n=k+1时:第k+1条直线分别与前k条直线各交于
一点,共增加k个点,由1)、2)可知,对一切n∈N?原命题均成立。(3)数学归纳法证明几何问题:练习1:凸n边形有f(n)条对角线,则凸n+1边形的对角线
的条数f(n+1)=f(n)+_________.n-1练习2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.2k(4)数学归纳法证明不等式问题:则当n=k+1时,我们有:即当n=k+1时,不等式也成立.证:(1)当n=1时,左边=1,右边=2, 不等式显然成立.则当n=k+1时,我们有:即当n=k+1时,不等式也成立.根据(1)、(2)可知,原不等式对一切正整数都 成立.即当n=k+1时,命题成立.例4、已知x> ?1,且x?0,n?N,n?2.
求证:(1+x)n>1+nx.(2)假设n=k时,不等式成立,即 (1+x)k>1+kx
当n=k+1时,因为x> ?1 ,所以1+x>0,于是
左边=(1+x)k+1=(1+x)k(1+x)>(1+x)(1+kx)=1+(k+1)x+kx2;
右边=1+(k+1)x.
因为kx2>0,所以左边>右边,即(1+x)k+1>1+(k+1)x.
这就是说,原不等式当n=k+1时也成立.
根据(1)和(2),原不等式对任何不小于2的自然数n都成立.证明: (1)当n=2时,左=(1+x)2=1+2x+x2
∵ x?0,∴ 1+2x+x2>1+2x=右
∴n=1时不等式成立则当n=k+1时, 有:即当n=k+1时,不等式成立. 五、小结:1.与正整数有关的数学命题可以考虑用数学归纳法证
明,但注意不要滥用.要掌握数学归纳法的实质与步
步. 2.归纳思想充分体现了辩证唯物主义的特殊与一般的
辨证思想,是数学的基本思想,数学归纳法体现了有
限辨证关系与转化的思想.3. 数学归纳法的应用通常与数学的其他方法联系在一
起的,如比较法、放缩法、配凑法、分析法和综合法
等. 数学归纳法的第一步是递推的基础,有了此基础,在
第二步中的假设才能成立,才不是真正意义上的纯粹假设. 第二步是递推的依据,当假设中的某些情况(n≥n0)
时n取值较小的情况)成为事实后,依据第二步就可知当n取下一个值时命题也成立,如此又增加了假设中变为命题成立的n的取值,经不断地循环递推便得到对满足n≥n0的所有正整数命题都成立.(1)重点:两个步骤、一个结论;注意:递推基础不可少,归纳假设要用到,结论写明莫忘掉。点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数f(n)=n(n-1)/2.说明:用数学归纳法证明几何问题,重难点是处理好当n=k+1时利用假设结合几何知识证明命题成立.注:在上例的题设条件下还可以有如下二个结论:(1)设这n条直线互相分割成f(n)条线段或射线,
---则: f(n)=n2.(2)这n条直线把平面分成(n2+n+2)/2个区域.1:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,
证明这n条直线把平面分成f(n)=(n2+n+2)/2个区域.作业1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.2:设有通过一点的k个平面,其中任何三个平面或
三个以上的平面不共有一条直线,这k个平面将
空间分成f(k)个区域,则k+1个平面将空间分成
f(k+1)=f(k)+__________个区域.思考题小结:
重点:两个步骤、一个结论;
注意:奠基基础不可少,
归纳假设要用到,
结论写明莫忘掉.一、复习回顾:什么是数学归纳法? 对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:(1)证明当n取第一个值n0(例如n0=1) 时命题成立;【归纳奠基】
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立
证明当n=k+1时命题也成立.
这种证明方法叫做 数学归纳法.数学归纳法【归纳递推】框图表示验证n=n0时命题成立若n=k(k≥n0)时命题成立,
证明n=k+1时命题也成立.归纳奠基归纳推理命题对从n0开始所有的正整数n都成立(1) 第一步,是否可省略? 不可以省略.(2)第二步,从n=k(k≥n0)时命题成立的假设出发,推证 n=k+1 时命题也成立.既然是假设,为什么还要把它当成条件呢?这一步是在第一步的正确性的基础上,证明传递性.想一想(1)当n=1,2,3,4时,计算f(n)的值.(2)你对f(n)的值有何猜想?用数学归纳法证明你的猜想.解:当n=1时, f(1) =51+2×31-1+1=8×1. 当n=2时, f(2) =52+2×32-1+1=8×4. 当n=3时, f(3) =53+2×33-1+1=8×18. 当n=4时, f(4) =54+2×34-1+1=8×35.例1 设n∈N*,5n+2×3n-1+1.证明 ①当n=1时,有f(1) =51+2×31-1+1=8能被8整除,命题成立.猜想:当n∈N*时, f(n) =5n+2×3n-1+1.能被8整除.②假设当n=k时命题成立,即f(k)能被8整除,那么当n=k+1时,有
f(k+1) =5k+1+2×3k+1-1+1
=5×5k+6×3k-1+1
=5×5k+2×3k-1+1+ 4(5k+3k-1)
= f(k)+4(5k+3k-1) 这里,5k和3k-1均为奇数,它们和(5k+3k-1)必为偶数,从而4(5k+3k-1)能被8整除.
由归纳假设,f(k)能被8整除,所以f(k+1)能被8整除,这就是说当n=k+1时命题也成立.
根据(1)(2),可知命题对于任意自然数都成立. 特别提示:
数学归纳法证题的关键是“一凑假设,二凑结论”,在证题的过程中,归纳推理一定要起到条件的作用,即证明n=k+1成立时必须用到归纳递推这一条件.(2)假设当n=k(k∈N+)时,命题成立,即有 ,当n=k+1时,当k+1条直线与前面k条直线有k个不同交点,即它被前面k条直线截成k+1段,其中每一段都把它所在的原区域一分为二,也即使原区域数目增加k+1.例2:平面上有n条直线,其中任意两条都相交,任意三条不共点,这些直线把平面分成多少个区域?
证明你的结论.解:这样的n条直线把平面分成的区域数目为 ,下面用数学归纳法证明: (1)当n=1时,一条直线将平面分成两部分,f(1)=2,∴n=1时,命题成立. 故当n=k+1时,命题成立.
由(1)(2)可知,对任意正整数n,命题成立.补充练习 有n个圆,其中每两个圆都相交于两点,并且每
三个圆都不相交于同一点,求证:这n个圆把平面分
成f(n)=n2-n+2个部分.证明:(1)当n=1时,即一个圆把平面分成二个部分, f(1)=2,又n=1时, n2-n+2=2,
∴命题成立.(2)假设当n=k时,命题成立,即k个圆把平面分成f(k)=k2-k+2个部分,那么由题意知第 k+1个圆与前k个圆中,每个圆交于两点,有无三圆交于同一点,于是它与其它k交于2k个点,把它分成2k条弧而每条弧把原区域分成2块,因此这个平面的总区域增加2k块,即f(k+1)=k2-k+2+2k=(k+1)2-(k+1)+2,即当n=k+1时,命题成立.
由(1)(2)可知,对任意的n∈N+,命题成立.1.用数学归纳法证明:1+2+22+…+2n-1=2n-1 (n∈N*).证明:(1)当n=1时,左边=1,右边=1,等式是成立的.
(2)假设当n=k时等式成立,就是
1+2+22+…+2k-1 =2k-1
那么, 1+2+22+…+2k-1 +2k=2k-1 + 2k
=2×2k-1
=2k+1-1
这就是说,当n=k+1时,等式也成立. 因此,根据(1)和(2)可断定,等式对于任何n∈N*都成立.练习3.求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1).用数学归纳法证明恒等式的步骤及注意事项:① 明确首取值n0并验证真假.(必不可少)
②“假设n=k时命题正确”并写出命题形式.
③分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别.弄清左端应增加的项.
④ 明确等式左端变形目标,掌握恒等式变形常用的
方法:乘法公式、因式分解、添拆项、配方等,
并用上假设.(1)证明当n取第一个值n0(如 n0=1或2等)时结论正确 数学归纳法是一种证明与正整数有关的数学命题的重要方法.主要有两个步骤一个结论: 【归纳奠基】.(2)假设n=k时结论正确,证明n=k+1时结论也正确(3)由(1),(2)得出结论.【归纳递推】.(1)2+4+6+8+…+2n=n2+n+1(n?N*)证明 :假设当n=k时等式成立,即
2+4+6+8+…+2k=k2+k+1(k?N*)那么,当n=k+1时,有
2+4+6+8+…+2k+2(k+1)
=k2+k+1+2(k+1)
=(k+1)2+(k+1)+1 ,
因此,对于任何n?N*等式都成立。缺乏“递推基础”事实上,我们可以用等差数列求和公式验证原等式是不成立的!
(3)(纠错题)课本P87 T3 2n>n2(n?N*)证明 :①当n=1时,21>12,不等式显然成立。
②假设当n=k时等式成立,即2k>k2,
那么当n=k+1时,有
2k+1=2?2k=2k+2k>k2+k2?k2+2k+1=(k+1)2.
这就是说,当n=k+1时不等式也成立。
根据(1)和(2),可知对任何n?N*不等式都成立。虽然既有“递推基础”,又用到假设(“递推依据”),但在证明过程中出现错误,故上述证法错误!事实上,原不等式不成立,如n=2时不等式就不成立。练习巩固 CC练习巩固 练习巩固 提什么
好呢?
注意结论的形式 练习巩固 5.求证:当n∈N*时,证明: 练习巩固 1.用数学归纳法证明:
在验证 n=1成立时,左边计算所得的结果是( ) A.1 B.
C. D. C例1、求证:(n+1)(n+2)…(n+n)=2n? 1? 3?… ?(2n-1)(一)用数学归纳法证明等式或不等式(2)假设当n=k(k≥2)时不等式成立,即有: 则当n=k+1时,我们有:即当n=k+1时,不等式也成立.例2.用数学归纳法证明:例3:利用数学归纳法证明不等式
(n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时,不等式左边的变化是( ):练习(1)用数学归纳法证: D(2)用数学归纳法证: (n≥2,n∈N )过程中,由“n=k”变到“n=k+1”时,左式所需添加的项数为( ):A.1项B. 项D. 项C. 项C(二)用数学归纳法证明整除问题(三)数学归纳法证明几何问题. 例:平面内有n条直线,其中任何两条不平行,任何三条不过同一点,证明这n条直线把平面分成f(n)=(n2+n+2)/2个部分.1:n边形有f(n)条对角线,则凸n+1边形的对角线 ------的条数f(n+1)=f(n)+_________.练习(四)归纳—猜想—证明(求数列的 通项公式)(五)用数学归纳法证明探究性问题点拨:对这种类型的题目,一般先利用n的特殊值,探求出待定系数,然后用数学归纳法证明它对一切正整数n都成立.则当n=k+1时,故当n=k+1时,结论也正确.根据(1)、(2)知,对一切正整数n,结论正确.(1)当n=1时,由上面解法知结论正确.例:比较 2n 与 n2 (n∈N*)的大小注:先猜想,再证明解:当n=1时,2n=2,n2=1, 2n>n2
当n=2时,2n=4,n2=4, 2n=n2
当n=3时,2n=8,n2=9, 2n
当n=5时,2n=32,n2=25, 2n>n2
当n=6时,2n=64,n2=36, 2n>n2
猜想当n≥5时,2n>n2(证明略)
证明:(1)当 时,不等式 显然成立 用数学归纳法证明: (2)假设 时不等式成立,即
那么,当 时,有 即当 时不等式也成立. 根据(1)(2),可知对任何 ,不等式都成立. [研一题][悟一法] 用数学归纳法证明与正整数有关的等式时,关键在于“看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与n的取值是否有关,由n=k到n=k+1时,等式两边会增加哪些项.[研一题][悟一法]
用数学归纳法证明不等式时要注意两凑:一凑归纳假设;二凑证明目标,在凑证明目标时,比较法、综合法、分析法都可选用.[通一类][研一题][悟一法]
解决此类问题的基本思路是:可以先从观察入手,发现问题的特点,以形成解决问题的初步思路,然后用归纳的方法进行试探,提出猜想,最后用数学归纳法给出证明.[通一类]3.已知数列{an}中,Sn是{an}的前n项和,且Sn是2a与-
2nan的等差中项,其中a是不等于零的常数.
(1)求a1,a2,a3;
(2)猜想an的表达式,并用数学归纳法加以证明.[悟一法]
(1)用数学归纳法证明几何命题时一要注意数形结合,二要注意有必要的文字说明.
(2)证明几何问题的关键是由n=k到n=k+1时f(n)的增加量,解题时可先用f(k+1)-f(k)得出结果,再结合图形给予说明.[通一类]4.平面内有n(n∈N*)个圆,其中每两个圆都相交于两点,
且每三个圆都不相交于同一点,求证:这n个圆把平面分成n2-n+2部分.
证明:(1)当n=1时,n2-n+2=2,即一个圆把平面分成两部分,故结论成立.
(2)假设当n=k(k≥1,k∈N*)时命题成立,即k个圆把平面分成k2-k+2部分.则当n=k+1时,这k+1个圆中的k个圆把平面分成k2-k+2个部分,第k+1个圆被前k个圆分成2k条弧,这2k条弧中的每一条把它所在的平面部分都分成两部分,这样共增加2k个部分,故k+1个圆把平面分成k2-k+2+2k=(k+1)2-(k+1)+2部分,即n=k+1时命题也成立.
综上所述,对一切n∈N*,命题都成立. [错因] 错解在证明当n=k+1等式成立时,没有用到归纳假设“当n=k(k∈N*)时等式成立”,故不符合数学归纳法证题的要求.(2)数学归纳法证题的步骤:两个步骤,一个结论; (3)数学归纳法优点:即克服了完全归纳法的繁杂的缺
点,又克服了不完全归纳法结论不可靠的不足。(4)数学归纳法的基本思想:运用“有限”的手段来
解决“无限”的问题(1)数学归纳法是一种证明与正整数有关的数学命题
的重要方法回顾反思
