数学广角——搭配例1(课件)——二年级上册数学 人教版(共16张PPT)
文档属性
| 名称 | 数学广角——搭配例1(课件)——二年级上册数学 人教版(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 06:21:08 | ||
图片预览



文档简介
(共16张PPT)
数学广角——搭配(一)
例1 简单的搭配
今天我们要去数学广角,必须先打开这扇门。
密码是是由1和2组成的,想一想,可能是多少?
2
1
2
1
创设情境
探究新知
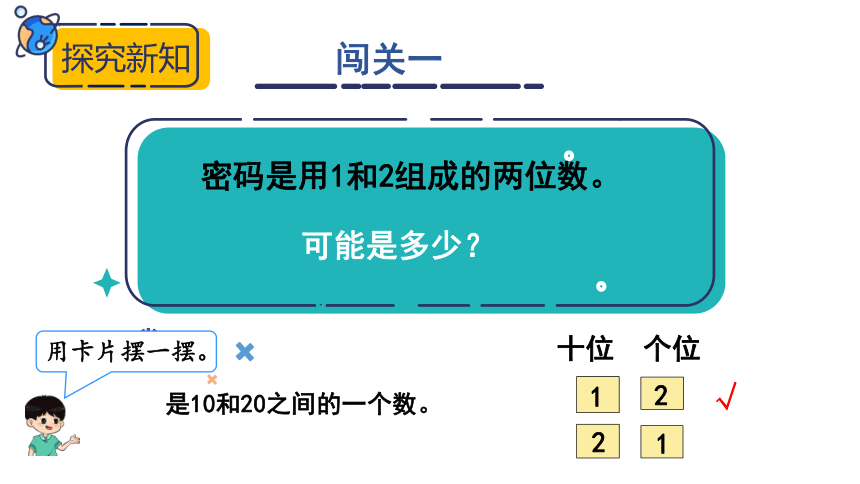
密码是用1和2组成的两位数。
可能是多少?
1
2
1
2
十位 个位
是10和20之间的一个数。
√
用卡片摆一摆。
闯关一
探究新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
闯关二
我用卡片摆一摆。
3
2
1
3
2
1
1
3
2
1
2
3
1
2
3
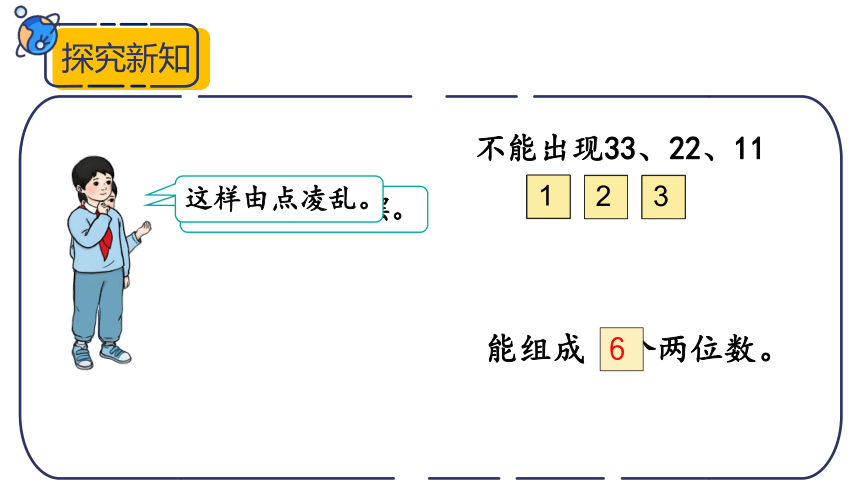
这样由点凌乱。
能组成 个两位数。
6
不能出现33、22、11
探究新知
十位
个位
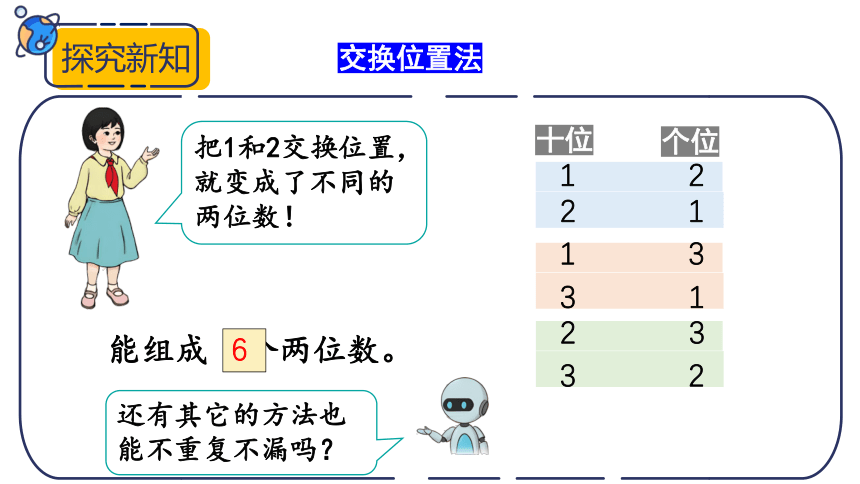
把1和2交换位置,就变成了不同的两位数!
1
2
2
1
1
3
3
1
2
3
3
2
能组成 个两位数。
6
还有其它的方法也能不重复不漏吗?
探究新知
交换位置法
十位
个位
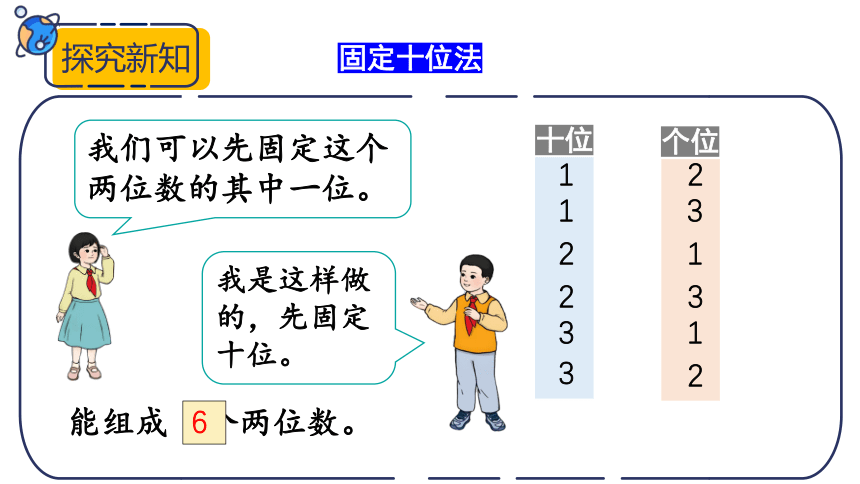
我是这样做的,先固定十位。
我们可以先固定这个两位数的其中一位。
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
固定十位法
十位
个位
还可以先固定个位。
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
固定个位法
对比观察,想一想:
要想不重复不遗漏。就要有序思考,可以一一列举出来。
探究新知
交换法
固定法
用数字1、2和0组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
十位 个位
1
2
2
1
1
0
2
0
0不能放在最高位。
能组成4个两位数。
拓展延伸
用三个不同的数字组成十位数和个位数不重复的两位数:
交换法:每次选2个数,交换位置写出不同的两位数。
(0不能在十位上)
固定法:将两位数中的其中一位固定,再把其余的数字
依次和它组合。从而写出所有可能的数。
方法小结
想一想,怎样做才能不重不漏?
北城 南城
用 、 和 3种颜色中选出2种颜色,给地图上的2个城区涂上不同的颜色,一共有多少种涂色方法?
做一做
巩固练习
1. 有2名同学坐成一排合影,有多少种坐法?3名呢?
巩固练习
② ①
① ②
① ②
答:2名同学站成一排合影,有2种坐法。
巩固练习
① ② ③
2. 有2名同学坐成一排合影,有多少种坐法?3名呢?
① ② ③
① ③ ②
② ① ③
② ③ ①
③ ① ②
③ ② ①
答:3名同学站成一排合影,有6种站法。
3.从下面3本书中选2本,送给小丽、小清各1本,一共有多少种送法?
1
2
A
B
C
答:一共6种送法。
巩固练习
儿童文学 数学趣题 自然奥秘
小丽
小清
小清
小丽
小丽
小清
小丽
小清
小丽
小清
小丽
小清
感谢观看
数学广角——搭配(一)
例1 简单的搭配
今天我们要去数学广角,必须先打开这扇门。
密码是是由1和2组成的,想一想,可能是多少?
2
1
2
1
创设情境
探究新知
密码是用1和2组成的两位数。
可能是多少?
1
2
1
2
十位 个位
是10和20之间的一个数。
√
用卡片摆一摆。
闯关一
探究新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
闯关二
我用卡片摆一摆。
3
2
1
3
2
1
1
3
2
1
2
3
1
2
3
这样由点凌乱。
能组成 个两位数。
6
不能出现33、22、11
探究新知
十位
个位
把1和2交换位置,就变成了不同的两位数!
1
2
2
1
1
3
3
1
2
3
3
2
能组成 个两位数。
6
还有其它的方法也能不重复不漏吗?
探究新知
交换位置法
十位
个位
我是这样做的,先固定十位。
我们可以先固定这个两位数的其中一位。
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
固定十位法
十位
个位
还可以先固定个位。
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
固定个位法
对比观察,想一想:
要想不重复不遗漏。就要有序思考,可以一一列举出来。
探究新知
交换法
固定法
用数字1、2和0组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
十位 个位
1
2
2
1
1
0
2
0
0不能放在最高位。
能组成4个两位数。
拓展延伸
用三个不同的数字组成十位数和个位数不重复的两位数:
交换法:每次选2个数,交换位置写出不同的两位数。
(0不能在十位上)
固定法:将两位数中的其中一位固定,再把其余的数字
依次和它组合。从而写出所有可能的数。
方法小结
想一想,怎样做才能不重不漏?
北城 南城
用 、 和 3种颜色中选出2种颜色,给地图上的2个城区涂上不同的颜色,一共有多少种涂色方法?
做一做
巩固练习
1. 有2名同学坐成一排合影,有多少种坐法?3名呢?
巩固练习
② ①
① ②
① ②
答:2名同学站成一排合影,有2种坐法。
巩固练习
① ② ③
2. 有2名同学坐成一排合影,有多少种坐法?3名呢?
① ② ③
① ③ ②
② ① ③
② ③ ①
③ ① ②
③ ② ①
答:3名同学站成一排合影,有6种站法。
3.从下面3本书中选2本,送给小丽、小清各1本,一共有多少种送法?
1
2
A
B
C
答:一共6种送法。
巩固练习
儿童文学 数学趣题 自然奥秘
小丽
小清
小清
小丽
小丽
小清
小丽
小清
小丽
小清
小丽
小清
感谢观看
