3.1 圆 课件 (共36张PPT)

(共36张PPT)
第三章 圆
3.1 圆
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握圆的基本概念和圆的画法，学会圆的表示方法；
2、认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，并了解它们之间的区别和联系.
3、掌握点与圆之间的位置关系，学会用学术用语来表示；
导入新课
观察与思考
观察上面的图片，你发现了有什么共同点了吗？
圆
小学我们就学过如何画圆，这节课我们来探究一下圆的相关概念吧
讲授新课
知识点一 探究圆的概念
探究归纳
·
r
O
A
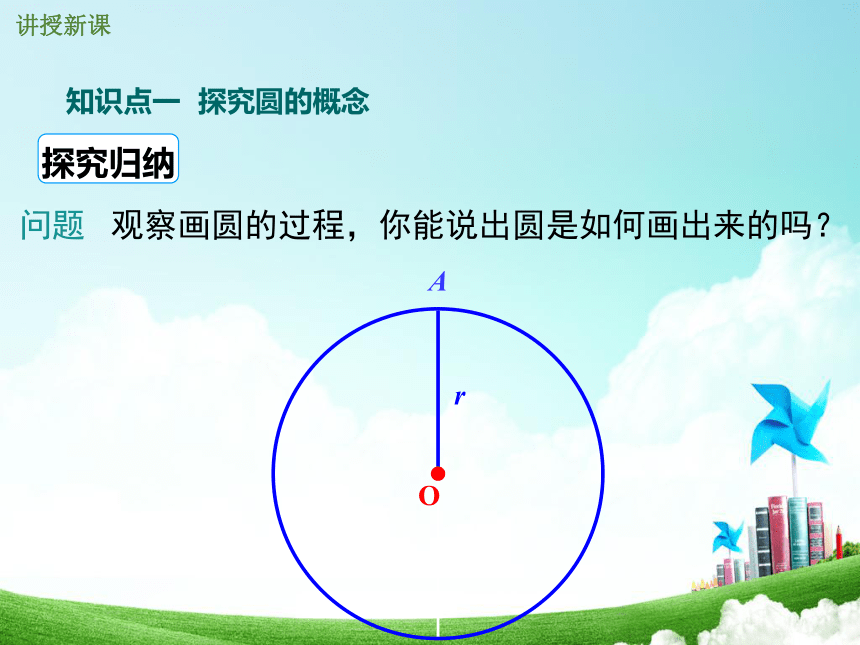
问题 观察画圆的过程，你能说出圆是如何画出来的吗？
圆的旋转定义
在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点所形成的图形叫做圆．以点O为圆心的圆，记作“⊙O”，读作“圆O”.
有关概念
固定的端点O叫做圆心，线段OA叫做半径，一般用r表示．
（1）圆上各点到定点（圆心O）的距离都等于 ．
（2）到定点的距离等于定长的点都在 ．
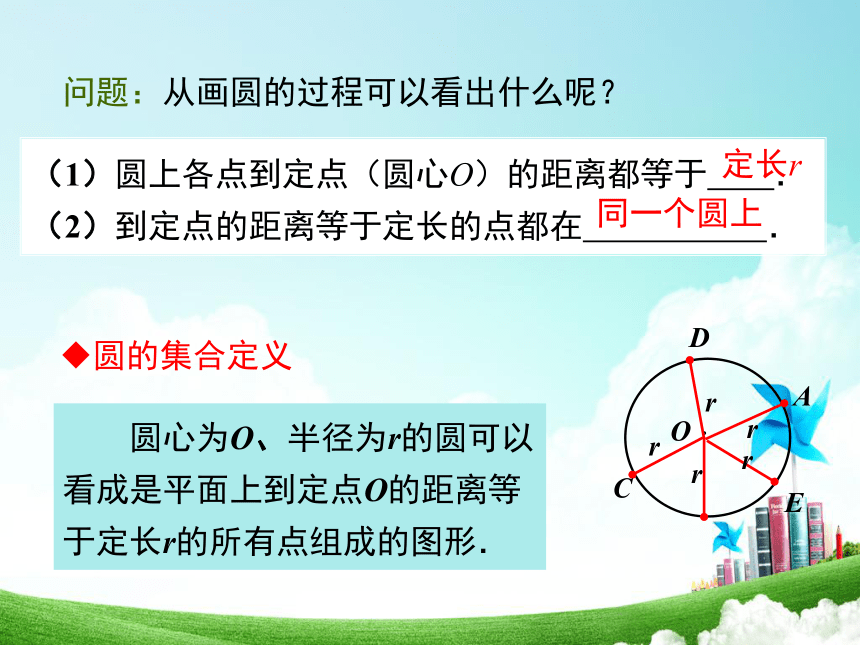
圆心为O、半径为r的圆可以看成是平面上到定点O的距离等于定长r的所有点组成的图形．
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
圆的集合定义
问题：从画圆的过程可以看出什么呢？
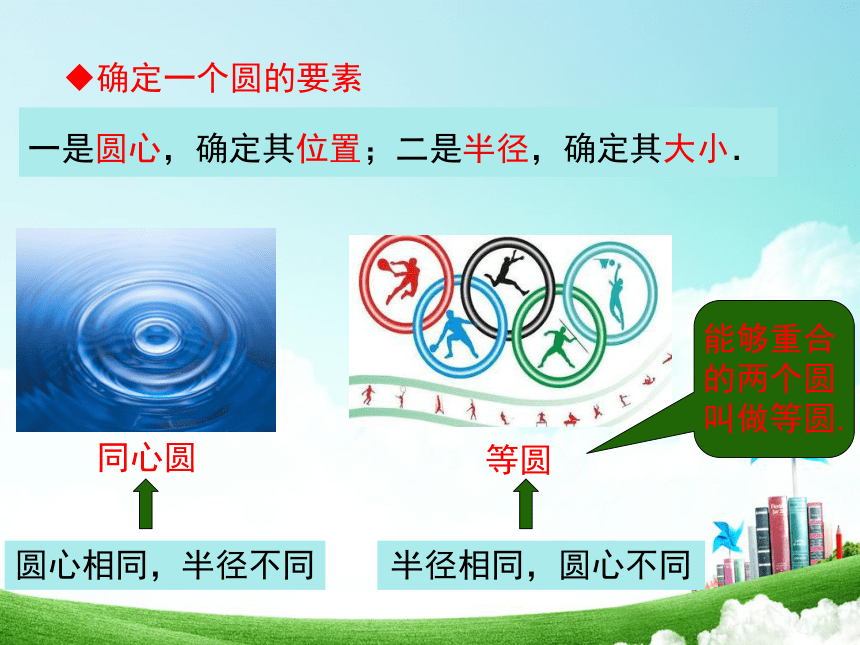
一是圆心，确定其位置；二是半径，确定其大小．
同心圆
等圆
半径相同，圆心不同
圆心相同，半径不同
确定一个圆的要素
能够重合的两个圆叫做等圆.
典例精析
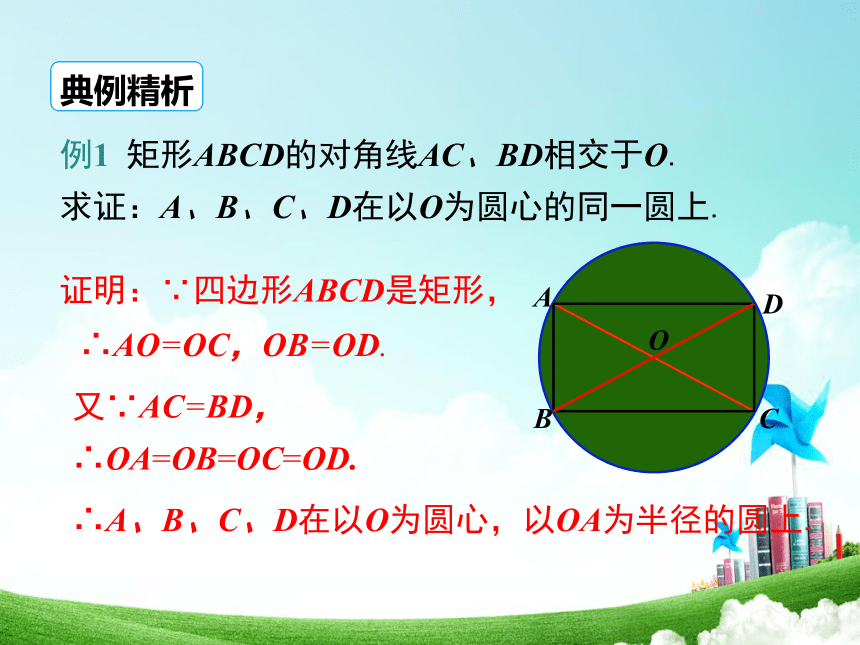
例1 矩形ABCD的对角线AC、BD相交于O.
求证：A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明：∵四边形ABCD是矩形，
∴AO=OC，OB=OD.
又∵AC=BD，
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心，以OA为半径的圆上.
知识点二 圆的有关概念
弦:
·
C
O
A
B
连接圆上任意两点的线段（如图中的AC）叫做弦.
经过圆心的弦（如图中的AB）叫做直径．
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦，是圆中最长的弦，但弦不一定是直径.
注意
弧:
·
C
O
A
B
圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
半圆
圆上任意两点间的部分叫做圆弧，简称弧．
以A、B为端点的弧记作 AB ，读作“圆弧AB”或“弧AB”．
(
等弧:
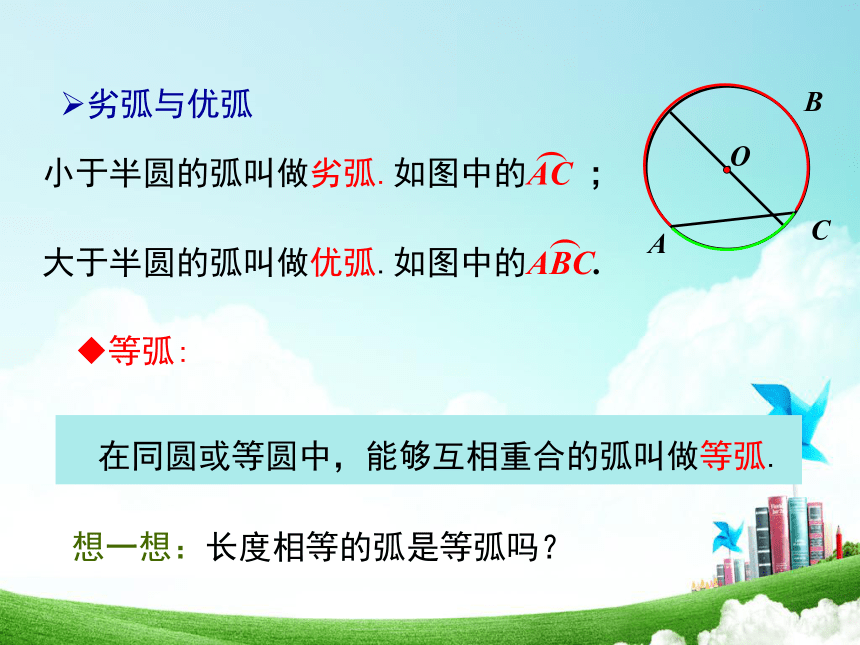
在同圆或等圆中，能够互相重合的弧叫做等弧.
想一想：长度相等的弧是等弧吗？
劣弧与优弧
·
C
O
A
B
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
如图.
(1)请写出以点A为端点的优弧及劣弧;
(2)请写出以点A为端点的弦及直径.
弦AF,AB,AC.其中弦AB又是直径.
（3）请任选一条弦，写出这条弦所对的弧.
答案不唯一，如：弦AF,它所对的弧是 .
A
B
C
E
F
D
O
劣弧：
优弧：
AF,
(
AD,
(
AC,
(
AE.
(
AFE,
(
AFC,
(
AED,
(
AEF.
(
AF
(
练一练
x
x
x
x
变式：如图，在扇形MON中， ，半径MO=NO=10，,正方形ABCD的顶点B、C、D在半径上，顶点A在圆弧上，求正方形ABCD的边长.
解：连接OA.
∵ABCD为正方形
∴DC=CO
设OC=x,则AB=BC=DC=OC=x
又∵OA=OM=10
∴在Rt△ABO中,
∴AB=BC=CD,∠ABC=∠DCB=90°
又∵∠DOC=45°
知识点三 点和圆的位置关系
.
问题1：观察下图，其中点和圆的位置关系有哪几种？
.
o
.
C
.
.
.
. B
.
.A
点与圆的位置关系有三种：
点在圆内，点在圆上，点在圆外.
问题2：设点到圆心的距离为d,圆的半径为r，量一量在点和圆三种不同位置关系时，d与r有怎样的数量关系？
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
＜
r
r
=
＞
r
反过来，由d与r的数量关系，怎样判定点与圆的位置关系呢？
要点归纳
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r＜d＜R
数形结合：
位置关系
数量关系
例：如图，已知矩形ABCD的边AB=6，AD=8.
以A为圆心，4为半径作⊙A，则点B、C、D与⊙A的位置关系如何？
解：AD=48=r，故D点在⊙A上
AB=6AC=10>r，故C点在⊙A外
当堂练习
1．若○A半径为5，圆心A的坐标是(1,2)，点P的坐标是(5,2)，那么点P与○A的位置关系为( )
A．点P在○A内 B．点P在○A上
C．点P在○A外 D．无法确定
【答案】A
【分析】先求出PA的长，然后比较PA与半径的大小，再根据点与圆的关系的判定方法进行判断．
【详解】解：∵点A的坐标是(1,2)，点P的坐标是(5,2)，
∴PA=4＜5，
∴点P在○A内，
故选：A．
2．已知⊙O的半径是4，点P到圆心O的距离d为方程x2-4x-5=0的一个根，则点P与⊙O的位置关系为（ ）
A．点P在⊙O内 B．点P在⊙O上
C．点P在⊙O外 D．不能确定
【详解】方程x2-4x-5=0的根为x1=5,x2=-1，
∵点P到圆心O的距离d为方程x2-4x-5=0的一个根，
∴d=5，
∵⊙O的半径是4，
d＞r，
∴点P在⊙O外，
故选：C．
3．如图，图中⊙O的弦共有（ ）
A．1条 B．2条 C．3条 D．4条
【答案】C
【分析】根据弦的定义即可求解． 连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径，直径是一个圆里最长的弦．
4．如图所示，已知矩形ABCD的边AB=3cm,AD=4cm若以点A为圆心作○A，使B,C,D三点中至少有一个点在圆内，且至少有一点在圆外，则○A的半径r的取值范围是（ ）
A．3＜r＜4 B．4＜r＜5
C．3＜r＜5 D．4＜r＜5
【答案】C
【分析】根据勾股定理求出AC的长，进而得出点B,C,D与A的位置关系，即可得出半径r的取值范围．
5．若有一点到圆上最小距离为2cm，最大距离8cm，则圆的半径为_________cm．
【答案】3或5
【分析】由于点与圆的位置关系不能确定，故应分两种情况进行讨论，即点在圆内和点在圆外分别求解即可．
6．有一长、宽分别为4cm、3cm的矩形ABCD，以A为圆心作圆，若B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则○O的半径r的取值范围是_____．
【答案】3cm＜r＜5cm
【分析】由题意结合勾股定理可求矩形ABCD对角线的长，再根据B,C,D三点到点A的最大距离为5cm，最小距离为3cm，所以要B,C,D三点中至少有一点在圆内，且至少有一点在圆外，就应当使○O的半径大于最小的距离3cm，小于最大的距离5cm，即得出答案．
7．点P与圆上一点的连线中，最长的为11cm，最短的为5cm，则圆的半径为_____cm．
【答案】8或3
【分析】本题应分为两种情况来讨论，关键是得出：当点P在⊙O内时，直径=最近点的距离+最远点的距离；当点P在⊙O外时，直径=最远点的距离-最近点的距离．然后根据半径=直径的一半即可解答．
【详解】解：点P应分为位于圆的内部与外部两种情况讨论：
①当点P在圆内时，最近点的距离为5cm，最远点的距离为11cm,则直径是5+11=15cm，因而半径是8cm；
②当点P在圆外时，最近点的距离为5cm，最远点的距离为11cm，则直径是11-5=6cm，因而半径是3cm．
故该圆的半径是8cm或3cm．
故答案为：8或3．
8．如图，在矩形ABCD中，AB=8，AD=6，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点不在圆内，则r的取值范围是 _____．
【答案】6＜r＜10
【分析】先根据矩形性质和勾股定理求出BD，再根据点与圆的位置关系结合图形即可得出结论．
【点睛】本题考查点与圆的位置关系、勾股定理和矩形的性质，解答关键是熟知点与圆的位置关系：设圆半径为r，点与圆心的距离为d，当d＜r时，点在圆内；当d=r时，点在圆上；当d＞r时，点在圆外．
9．圆圆在解答问题“在矩形ABCD中，AB=6,AD=8,以A为圆心作○A，使得B，C，D三点中至少有一点在○A内，有一点在○A外，求○A的半径r的取值范围？”时，答案为“6＜r＜8”．圆圆的答案对吗？如果错误，请写出正确的解答过程．
【答案】不正确，正确过程见解析
【详解】解：圆圆的结果不正确．
连接AC，
∵四边形ABCD为矩形，
∴∠B=90°，
根据勾股定理得：AC=10，
∵B，C，D三点中至少有一点在○A内，有一点在○A外，
∴点B在圆内，点C在圆外，
∴6＜r＜10，
∴圆圆的结果不正确．
10．如图，在矩形ABCD中，AB=6cm，AD=8cm，
(1)若以A为圆心，6cm长为半径作⊙A（画图），则B、C、D与圆的位置关系是什么？
(2)若作⊙A，使B、C、D三点至少有一个点在⊙A内，至少有一点在⊙A外，则⊙A的半径r的取值范围是______．
（1）
由图可知：点B在圆上，点C和点D在圆外．
（2）
连接AC，在Rt△ABC中，AC=10，
∴6故答案为：6课堂小结
圆
定义
旋转定义
要画一个确定的圆，关键是
确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦（直径）
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
点P在圆环内
r≤d≤R
R
r
P