3.2 圆的对称性 课件 (共30张PPT)
文档属性
| 名称 | 3.2 圆的对称性 课件 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 16:45:37 | ||
图片预览



文档简介
(共30张PPT)
第三章 圆
3.2 圆的对称性
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握圆的对称性,理解圆既是轴对称图形,也是中心对称图形;
2、掌握圆心角、弧、弦之间关系定理并利用其解决相关问题.
3、在理解相关的圆心角、弧、弦之间的关系时,记得一定要带上同圆或等圆这个条件;
导入新课
观察与思考
观察图片,想一想,如何将一块蛋糕平均分成两块?四块?八块?分小组讨论一下;
讲授新课
知识点一 圆的对称性概念
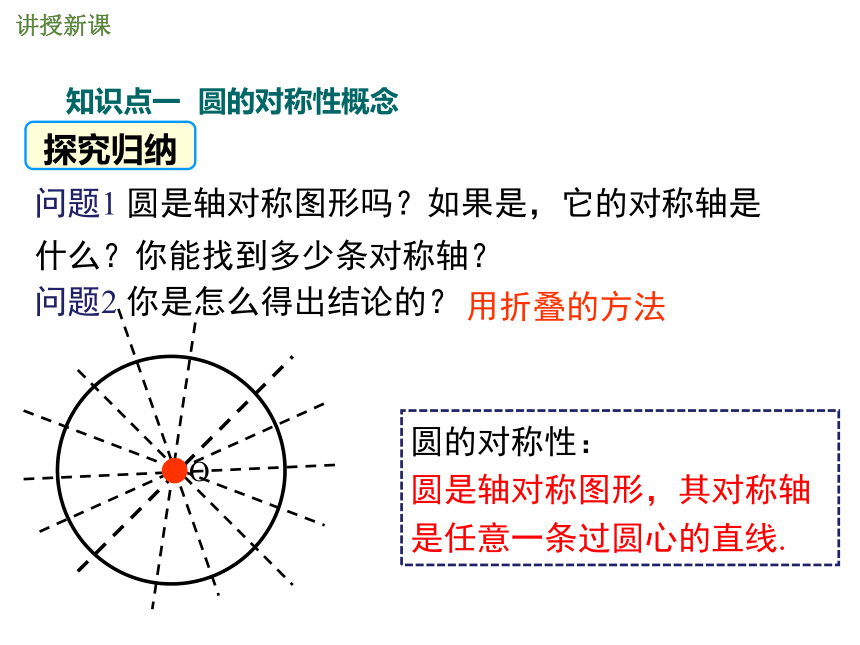
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
.
O
A
B
180°
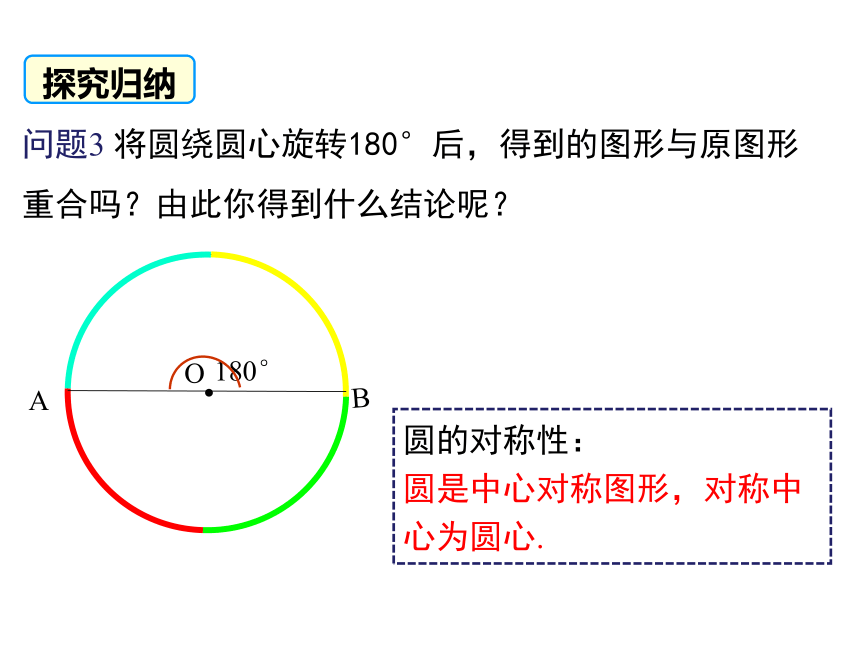
问题3 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性:
圆是中心对称图形,对称中心为圆心.
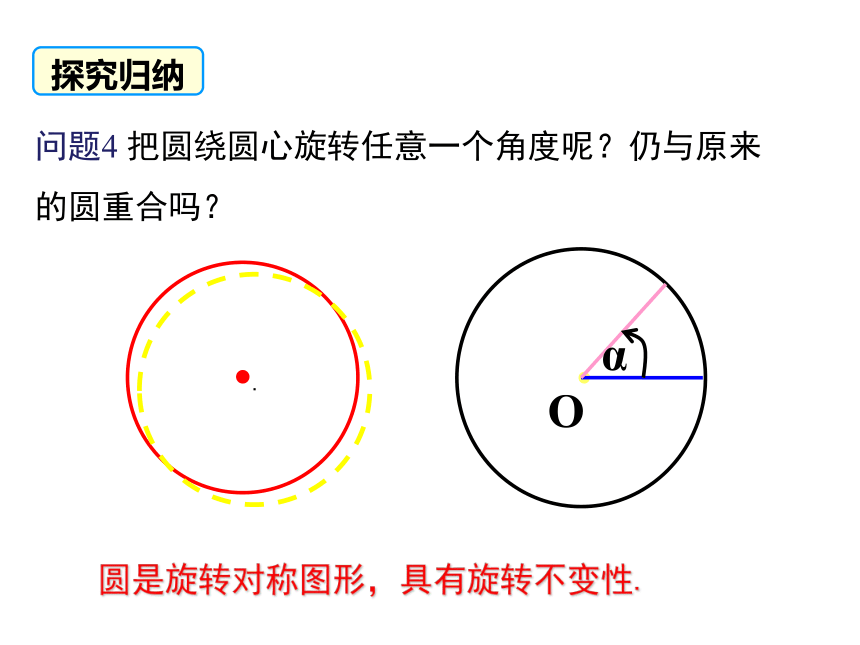
问题4 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
探究归纳
知识点二 圆心角、弧、弦之间的关系
在同圆中探究
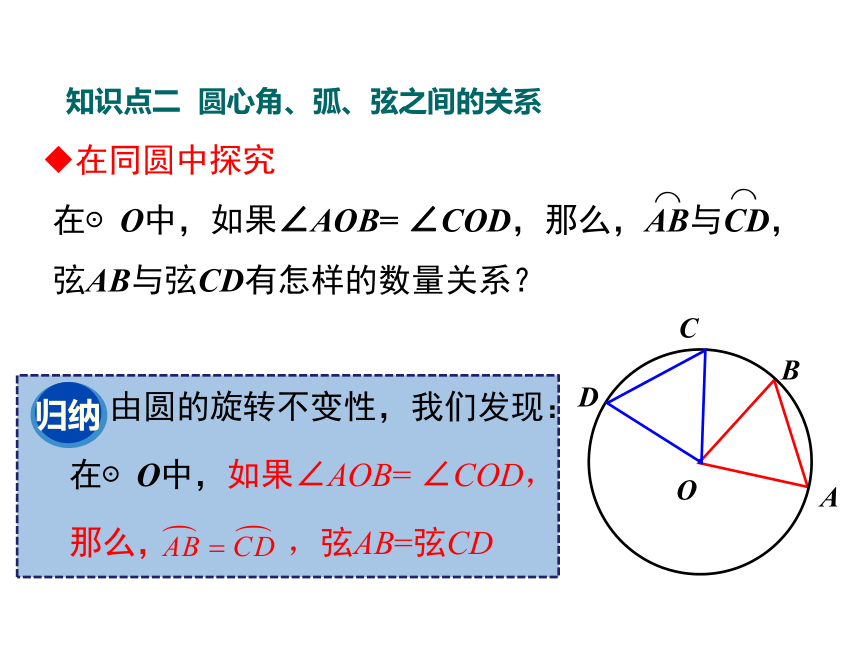
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
O ′
·
O
A
B
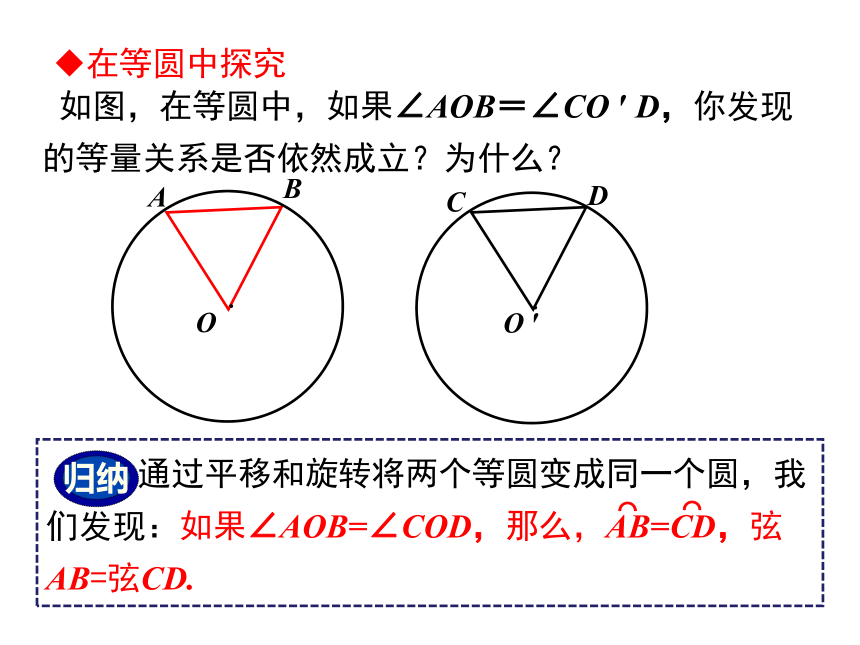
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
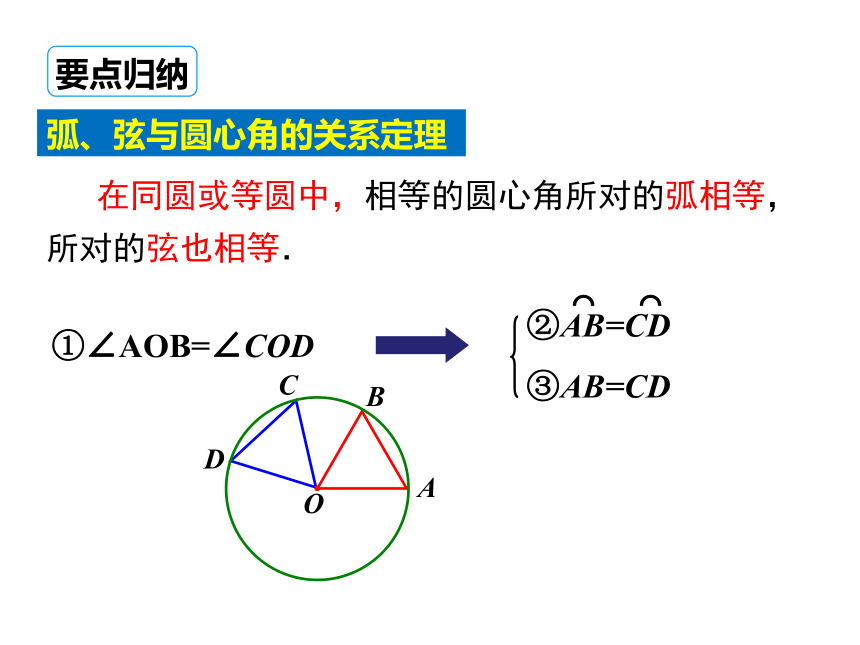
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
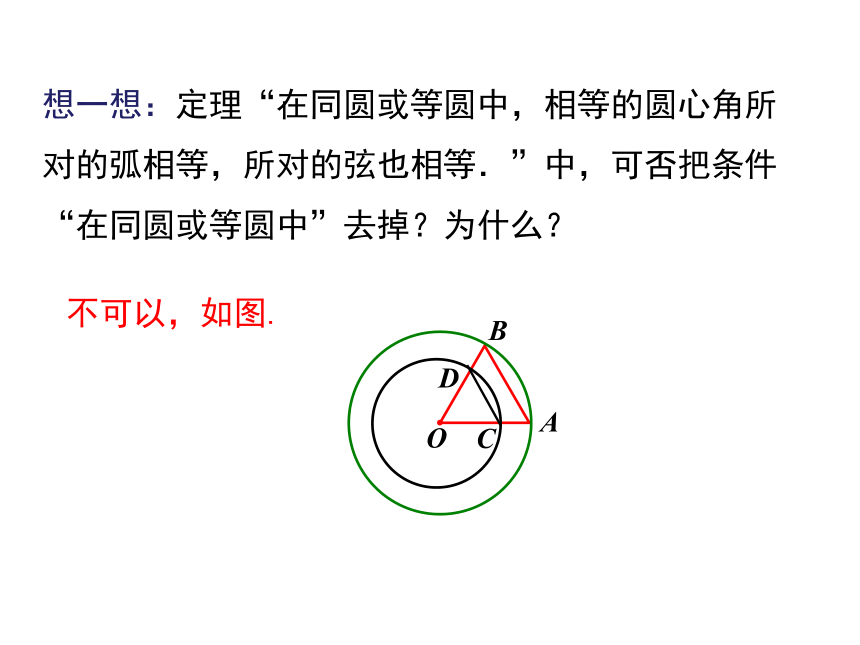
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
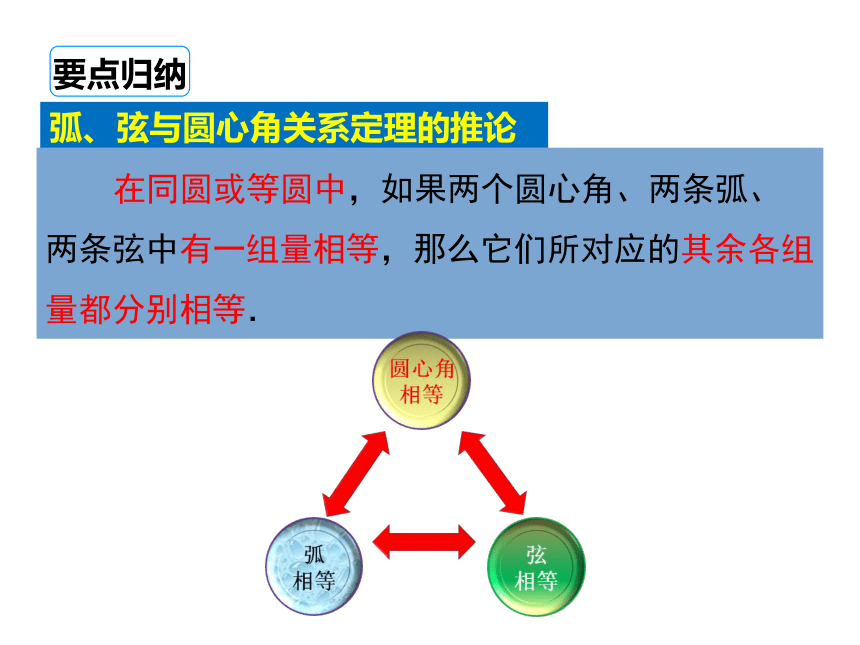
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
典例精析
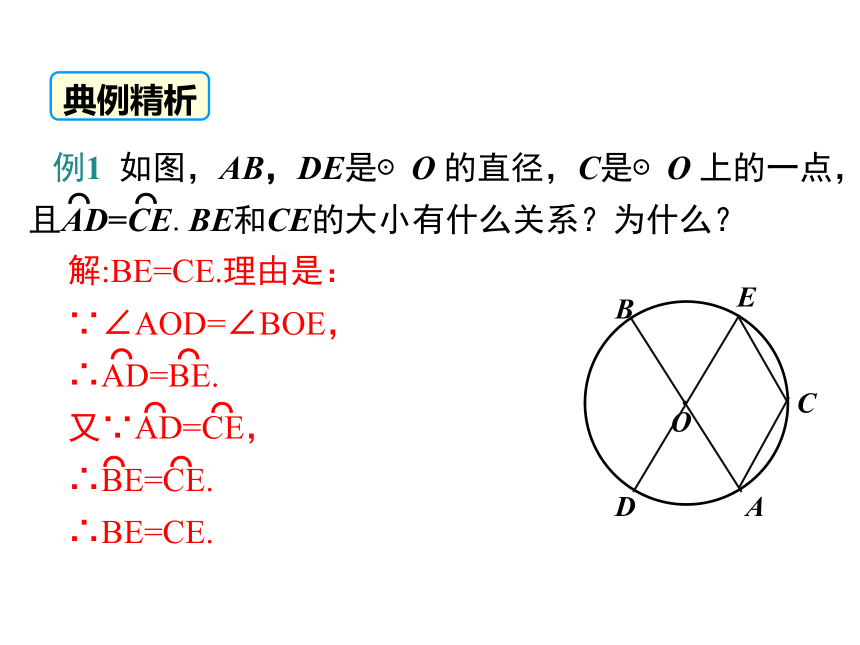
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
例2 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒ ⌒
当堂练习
1.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
【答案】D
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
2.如图,已知AB是○O的直径,弧BC=弧CD=弧DE,∠BOC=40°,那么∠AOE=( )
A.40° B.60° C.80° D.100°
【答案】B
【分析】先证明∠EOD=∠DOC=∠BOC=40°,∠BOE=3×40°=120°,再利用角的和差关系可得答案.
【点睛】本题考查的是弧与圆心角之间的关系,掌握“弧,弦,圆心角的关系”是解本题的关键.
3.如图,等腰三角形ABC的顶角∠BAC=36°,以腰AB为直径作圆,交BC于点D,交AC于点E,则弧DE的度数是( )
A.18° B.36° C.72° D.80°
【答案】B
【详解】解:设圆心为O,连接OE、OD,
∵AB=AC,
∴∠ABC=∠ACB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠ACB,
∴OD∥AC,
∴∠DOE=∠OEA,
∵OA=OE,
∴∠BAC=∠OEA,
∴∠DOE=∠BAC=36°,
即弧DE的度数为36°,
故选:B.
4.如图,AB是○O的直径,弧BC、弧CD与弧DE相等,∠COD=36°,则∠OEA的度数是( )
A.30° B.36° C.54° D.72°
【答案】C
【分析】由弧BC、弧CD与弧DE相等,得∠COB=∠COD=∠EOD,即可求∠AOE.
又因为OE和OA都是半径,长度相等,等边对等角,得∠OEA=∠AOE,根据三角形内角和180°就能求出∠OEA度数.
5.在半径为1的圆中,长度等于的弦所对的弧的度数为____________.
【答案】90°或270°
【分析】根据勾股定理的逆定理可知, 的弦与弦的端点两条长为1半径的围成的三角形是直角三角形.
6.如图,AB是⊙O的直径,D.C是弧BE的三等分点,∠COD=32°,则∠E的度数是___________.
【答案】48°
【分析】先运用等弧对等角得出∠EOB=96°,再利用三角形外角性质即可求解.
【详解】解:由C、D是BE的两个等分点,∠COD=32°知,∠BOC=∠DOE=∠COD=32°,
∴∠EOB=96°,
∵OE=OA,
∴∠AEO=∠EAO=,
故答案为:48°.
7.如图,BC是○O的弦,AD过圆心O,且AD⊥BC.若∠COD=40°,则∠A的度数为______.
【答案】20°
【详解】解:连接OB,延长AD交圆于E,
∵AD⊥BC,AD过圆心O,
∴弧BE=弧CE,
∴∠BOE=∠COD=40°,
∴∠A=∠BOE=20°,
故答案为:20°.
8.如图,在○O中,弧AB=弧BC=弧CD,连接AC,CD,则AC__2CD(填“>”,“< ”或“=” ).
【答案】<
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了三角形三边的关系.
9.如图,已知AB是○O的直径,弦AC∥OD.
(1)求证:弧BD=弧CD;
(2)若弧AC的度数为58°,求∠AOD的度数.
【答案】(1)见解析 (2)119°
【分析】(1)连接OC,根据等腰三角形的性质得出∠C=∠A,根据平行线的性质得出∠BOD=∠A,∠COD=∠C,求出∠COD=∠BOD,根据圆心角与弧的关系即可得证;
(2)求出∠BOC,求出∠COD,再求出答案即可.
10.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:
(1)AD=BC
(2)AE=CE.
【详解】(1)证明:∵AB=CD,
∴弧AB=弧CD,
∴弧AB-弧AC=弧CD-弧AC,
∴弧AD=弧BC,
∴AD=BC;
(2)∵∠ADE=∠CBE,∠AED=∠CEB,AD=BC
∴△ADE≌△CBE(AAS),
∴AE=EC.
课堂小结
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
圆心角
相等
弧
相等
弦
相等
在同圆或等圆中
第三章 圆
3.2 圆的对称性
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握圆的对称性,理解圆既是轴对称图形,也是中心对称图形;
2、掌握圆心角、弧、弦之间关系定理并利用其解决相关问题.
3、在理解相关的圆心角、弧、弦之间的关系时,记得一定要带上同圆或等圆这个条件;
导入新课
观察与思考
观察图片,想一想,如何将一块蛋糕平均分成两块?四块?八块?分小组讨论一下;
讲授新课
知识点一 圆的对称性概念
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
.
O
A
B
180°
问题3 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性:
圆是中心对称图形,对称中心为圆心.
问题4 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
探究归纳
知识点二 圆心角、弧、弦之间的关系
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
O ′
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
典例精析
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
例2 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒ ⌒
当堂练习
1.下列说法中,不正确的是( )
A.过圆心的弦是圆的直径 B.等弧的长度一定相等
C.周长相等的两个圆是等圆 D.直径是弦,半圆不是弧
【答案】D
【详解】A.直径是通过圆心且两个端点都在圆上的线段,故正确
B.能重合的弧叫等弧,长度相等,故正确
C.周长相等的圆其半径也相等,为等圆,故正确
D.直径是弦,半圆是弧,故错误
故选:D
2.如图,已知AB是○O的直径,弧BC=弧CD=弧DE,∠BOC=40°,那么∠AOE=( )
A.40° B.60° C.80° D.100°
【答案】B
【分析】先证明∠EOD=∠DOC=∠BOC=40°,∠BOE=3×40°=120°,再利用角的和差关系可得答案.
【点睛】本题考查的是弧与圆心角之间的关系,掌握“弧,弦,圆心角的关系”是解本题的关键.
3.如图,等腰三角形ABC的顶角∠BAC=36°,以腰AB为直径作圆,交BC于点D,交AC于点E,则弧DE的度数是( )
A.18° B.36° C.72° D.80°
【答案】B
【详解】解:设圆心为O,连接OE、OD,
∵AB=AC,
∴∠ABC=∠ACB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠ACB,
∴OD∥AC,
∴∠DOE=∠OEA,
∵OA=OE,
∴∠BAC=∠OEA,
∴∠DOE=∠BAC=36°,
即弧DE的度数为36°,
故选:B.
4.如图,AB是○O的直径,弧BC、弧CD与弧DE相等,∠COD=36°,则∠OEA的度数是( )
A.30° B.36° C.54° D.72°
【答案】C
【分析】由弧BC、弧CD与弧DE相等,得∠COB=∠COD=∠EOD,即可求∠AOE.
又因为OE和OA都是半径,长度相等,等边对等角,得∠OEA=∠AOE,根据三角形内角和180°就能求出∠OEA度数.
5.在半径为1的圆中,长度等于的弦所对的弧的度数为____________.
【答案】90°或270°
【分析】根据勾股定理的逆定理可知, 的弦与弦的端点两条长为1半径的围成的三角形是直角三角形.
6.如图,AB是⊙O的直径,D.C是弧BE的三等分点,∠COD=32°,则∠E的度数是___________.
【答案】48°
【分析】先运用等弧对等角得出∠EOB=96°,再利用三角形外角性质即可求解.
【详解】解:由C、D是BE的两个等分点,∠COD=32°知,∠BOC=∠DOE=∠COD=32°,
∴∠EOB=96°,
∵OE=OA,
∴∠AEO=∠EAO=,
故答案为:48°.
7.如图,BC是○O的弦,AD过圆心O,且AD⊥BC.若∠COD=40°,则∠A的度数为______.
【答案】20°
【详解】解:连接OB,延长AD交圆于E,
∵AD⊥BC,AD过圆心O,
∴弧BE=弧CE,
∴∠BOE=∠COD=40°,
∴∠A=∠BOE=20°,
故答案为:20°.
8.如图,在○O中,弧AB=弧BC=弧CD,连接AC,CD,则AC__2CD(填“>”,“< ”或“=” ).
【答案】<
【点睛】本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了三角形三边的关系.
9.如图,已知AB是○O的直径,弦AC∥OD.
(1)求证:弧BD=弧CD;
(2)若弧AC的度数为58°,求∠AOD的度数.
【答案】(1)见解析 (2)119°
【分析】(1)连接OC,根据等腰三角形的性质得出∠C=∠A,根据平行线的性质得出∠BOD=∠A,∠COD=∠C,求出∠COD=∠BOD,根据圆心角与弧的关系即可得证;
(2)求出∠BOC,求出∠COD,再求出答案即可.
10.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.求证:
(1)AD=BC
(2)AE=CE.
【详解】(1)证明:∵AB=CD,
∴弧AB=弧CD,
∴弧AB-弧AC=弧CD-弧AC,
∴弧AD=弧BC,
∴AD=BC;
(2)∵∠ADE=∠CBE,∠AED=∠CEB,AD=BC
∴△ADE≌△CBE(AAS),
∴AE=EC.
课堂小结
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
圆心角
相等
弧
相等
弦
相等
在同圆或等圆中
