3.5 确定圆的条件 课件 (共34张PPT)
文档属性
| 名称 | 3.5 确定圆的条件 课件 (共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 16:40:10 | ||
图片预览










文档简介
(共34张PPT)
第三章 圆
3.5 确定圆的条件
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解掌握圆的对称性和在圆中的相关概念;
2、掌握三点确定一个圆,并学会利用三个不在同一条直线的点画圆的方法;
3、理解并熟练掌握三角形的外接圆和外心的概念,并灵活运用三角形的外接圆解决问题;
导入新课
观察与思考
小明不小心打碎了镜子,假设打碎的镜子恰好如右图所示,那我们带哪一块镜片去商店就可以配好一个完整的镜子呢?
想一想,是什么原理呢?
讲授新课
知识点一 探索确定圆的条件
问题1如何过一个点A作一个圆?过点A可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
问题2如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
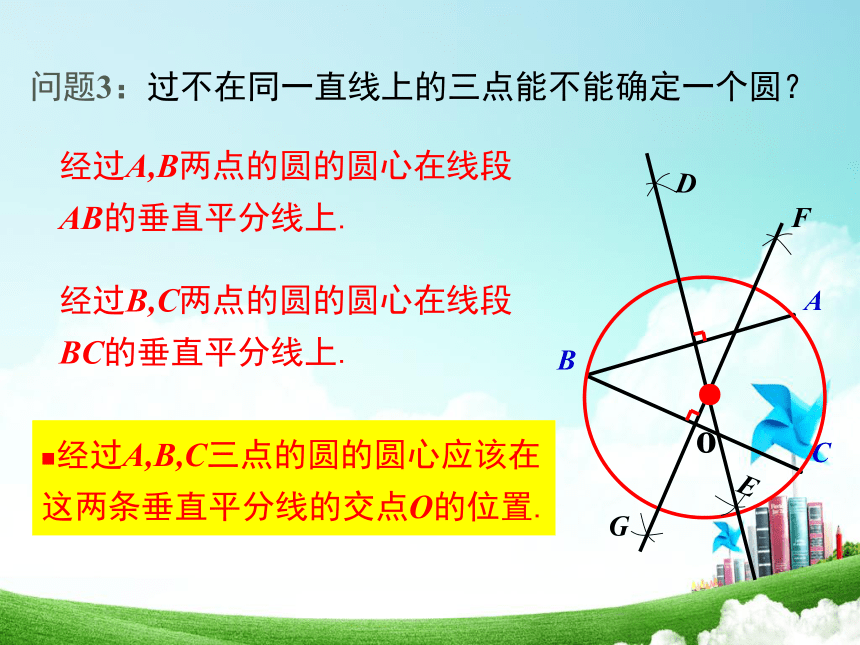
问题3:过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
A
B
C
问题4过同一直线上三点能不能作圆
不能.
有且只有
位置关系
A
B
C
D
E
G
F
●o
归纳总结
不在同一直线上的三个点确定一个圆.
例1 小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
典例精析
A.第①块 B.第②块
C.第③块 D.第④块
B
知识点二 三角形的外接圆和外心
试一试: 已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
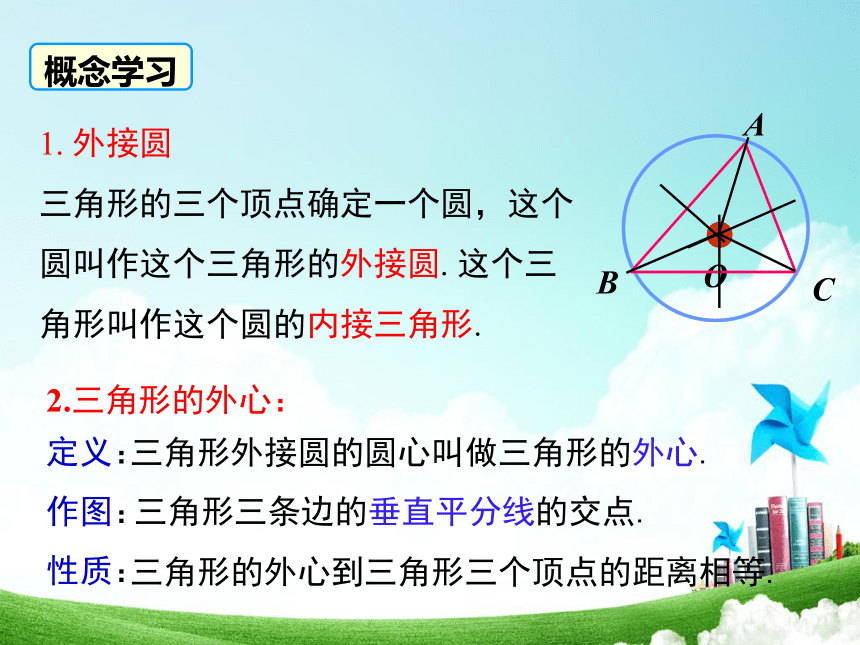
1. 外接圆
三角形的三个顶点确定一个圆,这个圆叫作这个三角形的外接圆. 这个三角形叫作这个圆的内接三角形.
三角形的外心到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三条边的垂直平分线的交点.
性质:
概念学习
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
要点归纳
例:如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在Rt△AOD中,
OA=OD·tan∠ADO= ,
AD=2OD=6,
∴点A的坐标是( ,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
当堂练习
1.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C均在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角直角坐标系,则过A,B,C三点的圆的圆心坐标为( )
A.(-1,-1) B.(-2,-1) C.(-1,-2) D.(-2,-2)
【答案】C
【详解】解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,则满足:
CD=DB=DA=,
∴点D是过A、B、C三点的圆的圆心,
即D的坐标为(-1,-2),
故选:C.
2.下列说法不正确的是( )
A.过不在同一直线上的三点能确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.相等的弧所对的弦相等
【答案】B
【分析】根据圆的性质举反例即可.
【详解】解:∵直径也是弦,直径之间都是互相平分,但不一定垂直,
∴B选项不正确,
故选B.
3.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为( )
A.:2π B.:4π
C.:π D.2:π
【详解】解:设该直角边是1,则斜边是2,另一条直角边是,
∴直角三角形的面积是,
外接圆的半径为1,面积是π×12=π,
∴这个直角三角形的面积与其外接圆的面积的比为:2π,
故选:A.
4.如图,已知锐角三角形ABC的顶点A到垂心H的距离等于它的外接圆半径,则∠BAC的度数为( )
A.30° B.45° C.60° D.75°
【答案】C
【分析】利用直径所对的圆周角的性质和垂心的性质判断出AH∥CD,CH∥AD,进而判断出CD=R,再判断出△COD是等边三角形,即可得出结论.
5.在Rt△ABC中,∠C=90°,AC=4,BC=3,则△ABC的外心在△ABC的______(填“内部”、“外部”或“边上”);其外接圆的半径为______.
【答案】 边上 2.5
【分析】根据直角三角形的外心在斜边上,即可判断△ABC外心的未知,根据勾股定理求出AB的长度,即可求出半径.
6.如图,小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是第________块.
【答案】①
【分析】根据不在一条直线上三点确定一个圆即可解得.
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心.只要有一段弧,即可确定圆心和半径.
所以小明带到商店去的一块玻璃碎片应该是①.
故答案为:①.
【点睛】本题考查的是垂径定理的推论的应用,确定圆的条件,掌握确定圆的的条件是解题的关键.
7.如图,点O是△ABC的外心,OD⊥AB,OE⊥AC,垂足分别为D、E,点M、N分别是OD、OE的中点,连接MN,若MN=1,则BC=______.
【详解】解:如图所示,连接DE,
∵O是△ABC的外心,OD⊥AB,OE⊥AC
∴AD=BD,AE=CE,
∴DE是△ABC中位线,
∴BC=2DE,
∵M、N分别是OD、DE的中点,
∴MN是△ODE的中位线,
∴DE=2MN=2,
∴BC=4,
故答案为:4.
8.如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0) ,(2,3),(3,1) .若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为______.
【答案】(4,3)或(5,2)或(1,2)
【分析】如图所示,以P为圆心,以PB的长为半径画圆,在圆上的格点即为所求.
【点睛】本题主要考查了坐标与图形,三角形外接圆,熟知点C在圆P上是解题的关键.
9.如图,已知正△ABC.
(1)请用直尺与圆规作正△ABC的外接圆,并保留作图痕迹;
(2)若点P是正△ABC的外接圆上的一点(不与点B,C重合),求∠BPC的度数.
【详解】(1)解:如图,
(2)如图,∠BPC=120°或60°
(2)分点P当在优弧BAC上时,当P在弧BC上时,分别讨论即可求解.
10.如图,在6×6的正方形网格中,圆上A,B,C三点都在格点上,请按要求作出图中圆的圆心:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
【详解】:如图所示,
(1)图1,找到AB,BC的垂直平分线交点即为所求;
(2)找到以AC为对角线的四个小正方形,根据网格经过这四个小正方形的对角线MN,则MN⊥AC,
根据BC的长度,构造正方形ABCD,DEFG,找到两个正方形的对角线交点PQ,连接PQ交MN于点O,点O即为所求
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
注意:同一直线上的三个点不能作圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
第三章 圆
3.5 确定圆的条件
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解掌握圆的对称性和在圆中的相关概念;
2、掌握三点确定一个圆,并学会利用三个不在同一条直线的点画圆的方法;
3、理解并熟练掌握三角形的外接圆和外心的概念,并灵活运用三角形的外接圆解决问题;
导入新课
观察与思考
小明不小心打碎了镜子,假设打碎的镜子恰好如右图所示,那我们带哪一块镜片去商店就可以配好一个完整的镜子呢?
想一想,是什么原理呢?
讲授新课
知识点一 探索确定圆的条件
问题1如何过一个点A作一个圆?过点A可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
问题2如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
问题3:过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
A
B
C
问题4过同一直线上三点能不能作圆
不能.
有且只有
位置关系
A
B
C
D
E
G
F
●o
归纳总结
不在同一直线上的三个点确定一个圆.
例1 小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
典例精析
A.第①块 B.第②块
C.第③块 D.第④块
B
知识点二 三角形的外接圆和外心
试一试: 已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
1. 外接圆
三角形的三个顶点确定一个圆,这个圆叫作这个三角形的外接圆. 这个三角形叫作这个圆的内接三角形.
三角形的外心到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三条边的垂直平分线的交点.
性质:
概念学习
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
要点归纳
例:如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在Rt△AOD中,
OA=OD·tan∠ADO= ,
AD=2OD=6,
∴点A的坐标是( ,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
当堂练习
1.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C均在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角直角坐标系,则过A,B,C三点的圆的圆心坐标为( )
A.(-1,-1) B.(-2,-1) C.(-1,-2) D.(-2,-2)
【答案】C
【详解】解:连接CB,作CB的垂直平分线,如图所示:
在CB的垂直平分线上找到一点D,则满足:
CD=DB=DA=,
∴点D是过A、B、C三点的圆的圆心,
即D的坐标为(-1,-2),
故选:C.
2.下列说法不正确的是( )
A.过不在同一直线上的三点能确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.相等的弧所对的弦相等
【答案】B
【分析】根据圆的性质举反例即可.
【详解】解:∵直径也是弦,直径之间都是互相平分,但不一定垂直,
∴B选项不正确,
故选B.
3.已知直角三角形的一条直角边等于它的外接圆的半径,则这个直角三角形的面积与其外接圆的面积的比为( )
A.:2π B.:4π
C.:π D.2:π
【详解】解:设该直角边是1,则斜边是2,另一条直角边是,
∴直角三角形的面积是,
外接圆的半径为1,面积是π×12=π,
∴这个直角三角形的面积与其外接圆的面积的比为:2π,
故选:A.
4.如图,已知锐角三角形ABC的顶点A到垂心H的距离等于它的外接圆半径,则∠BAC的度数为( )
A.30° B.45° C.60° D.75°
【答案】C
【分析】利用直径所对的圆周角的性质和垂心的性质判断出AH∥CD,CH∥AD,进而判断出CD=R,再判断出△COD是等边三角形,即可得出结论.
5.在Rt△ABC中,∠C=90°,AC=4,BC=3,则△ABC的外心在△ABC的______(填“内部”、“外部”或“边上”);其外接圆的半径为______.
【答案】 边上 2.5
【分析】根据直角三角形的外心在斜边上,即可判断△ABC外心的未知,根据勾股定理求出AB的长度,即可求出半径.
6.如图,小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是第________块.
【答案】①
【分析】根据不在一条直线上三点确定一个圆即可解得.
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心.只要有一段弧,即可确定圆心和半径.
所以小明带到商店去的一块玻璃碎片应该是①.
故答案为:①.
【点睛】本题考查的是垂径定理的推论的应用,确定圆的条件,掌握确定圆的的条件是解题的关键.
7.如图,点O是△ABC的外心,OD⊥AB,OE⊥AC,垂足分别为D、E,点M、N分别是OD、OE的中点,连接MN,若MN=1,则BC=______.
【详解】解:如图所示,连接DE,
∵O是△ABC的外心,OD⊥AB,OE⊥AC
∴AD=BD,AE=CE,
∴DE是△ABC中位线,
∴BC=2DE,
∵M、N分别是OD、DE的中点,
∴MN是△ODE的中位线,
∴DE=2MN=2,
∴BC=4,
故答案为:4.
8.如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0) ,(2,3),(3,1) .若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为______.
【答案】(4,3)或(5,2)或(1,2)
【分析】如图所示,以P为圆心,以PB的长为半径画圆,在圆上的格点即为所求.
【点睛】本题主要考查了坐标与图形,三角形外接圆,熟知点C在圆P上是解题的关键.
9.如图,已知正△ABC.
(1)请用直尺与圆规作正△ABC的外接圆,并保留作图痕迹;
(2)若点P是正△ABC的外接圆上的一点(不与点B,C重合),求∠BPC的度数.
【详解】(1)解:如图,
(2)如图,∠BPC=120°或60°
(2)分点P当在优弧BAC上时,当P在弧BC上时,分别讨论即可求解.
10.如图,在6×6的正方形网格中,圆上A,B,C三点都在格点上,请按要求作出图中圆的圆心:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹.
【详解】:如图所示,
(1)图1,找到AB,BC的垂直平分线交点即为所求;
(2)找到以AC为对角线的四个小正方形,根据网格经过这四个小正方形的对角线MN,则MN⊥AC,
根据BC的长度,构造正方形ABCD,DEFG,找到两个正方形的对角线交点PQ,连接PQ交MN于点O,点O即为所求
课堂小结
作圆
过一点可以作无数个圆
过两点可以作无数个圆
不在同一直线上的三个点确定一个圆
注意:同一直线上的三个点不能作圆
三角形外接圆
概念
性质
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外心
外接圆的圆心叫三角形的外心
