2022-2023学年人教版数学九年级上册(重庆地区)第二十五章 概率初步 期末复习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册(重庆地区)第二十五章 概率初步 期末复习题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 815.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 12:16:19 | ||
图片预览




文档简介
第二十五章 概率初步 期末复习题 2022-2023学年人教版数学九年级上册(重庆地区)
一、单选题
1.(2022·重庆永川·九年级期末)一个布袋里装有6个只有颜色不同的球,其中2个红球,4个白球.从布袋里任意摸出1个球,则摸出的球是白球的概率为( )
A. B. C. D.
2.(2022·重庆梁平·九年级期末)一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( )
A. B. C. D.
3.(2022·重庆渝中·九年级期末)下列说法错误的是( )
A.必然事件发生的概率是1 B.不可能事件发生的概率为0
C.随机事件发生的可能性越大,它的概率就越接近1 D.概率很小的事件不可能发生
4.(2022·重庆綦江·九年级期末)图2是由图1的窗户抽象出来的平面图形,半圆的直径与长方形的宽相等,此平面图形的对称轴与半圆的直径将图形分成四个部分,半圆的圆心点处有一任意转动指针,指针停止的位置是等可能的,则指针指向阴影部分的概率是( )
A. B.
C. D.因为长方形的长未知,所以概率不确定
5.(2022·重庆云阳·九年级期末)下列事件是随机事件的是( )
A.抛出的篮球会下落
B.经过有交通信号灯的路口,遇到红灯
C.任意画一个三角形,其内角和是
D.400人中有两人的生日在同一天
6.(2022·重庆梁平·九年级期末)如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,两个指针同时落在偶数上的概率是( ).
A. B. C. D.
7.(2022·重庆九龙坡·九年级期末)有4张正面分别标有数字、、0、3的卡片,它们除数字不同外其余全部相同.先将它们背面朝上,洗匀后从中随机抽取一张,得到的数记为m,不放回,再从剩余卡片中随机抽取一张,得到的数记为n,则使的概率为( )
A. B. C. D.
8.(2022·重庆黔江·九年级期末)在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在15%和35%,则口袋中白色球的个数可能是( )
A.6个 B.14个 C.20个 D.40个
二、填空题
9.(2022·重庆·中考真题)有三张完全一样正面分别写有字母A,B,C的卡片.将其背面朝上并洗匀,从中随机抽取一张,记下卡片上的字母后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的字母相同的概率是_________.
10.(2022·重庆·中考真题)不透明的袋子中装有个红球和个白球,除颜色外无其他差别,随机摸出一个球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率是________.
11.(2022·重庆市武隆区江口中学校九年级期末)在桌面上放有四张背面完全一样的卡片.卡片的正面分别标有数字﹣1,0,1,3.把四张卡片背面朝上,随机抽取一张,记下数字且放回洗匀,再从中随机抽取一张.则两次抽取卡片上的数字之积为负数的概率是_______.
12.(2022·重庆渝中·九年级期末)从,0,1,2这四个数中任取一个数,作为关于x的方程中a的值,则该方程有实数根的概率为_________.
13.(2022·重庆梁平·九年级期末)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有个相同的乒乓球,乒乓球上分别标有“元”、“元”、“元”、“元”的字样.规定:顾客在本超市一次性消费满元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费元,则该顾客所获得购物券的金额不低于元的概率是________.
14.(2022·重庆开州·九年级期末)将2本艺术类、4本文学类、6本科技类的书籍混在一起.若小陈从中随机抽取一本,则抽中文学类的概率为__________.
15.(2022·重庆巴蜀中学九年级期末)有四张完全相同的卡片,正面分别标有数字,,,,将四张卡片背面朝上,任抽一张卡片,卡片上的数字记为,再从剩下卡片中抽一张,卡片上的数字记为,则二次函数的对称轴在轴左侧的概率是__________.
16.(2022·重庆南开中学九年级期末)在一个不透明的口袋里装有除标号外完全一样的三个小球,小球上分别标有2,﹣1,3这三个数字,从袋中随机摸出一个小球,记标号为a,然后放回摇匀后再随机摸出一个小球,记标号为b,则满足的概率是______.
17.(2022·重庆八中九年级期末)现有A、B两个不透明的袋子,各装有三个小球,A袋中的三个小球上分别标记数字1,2,3;B袋中的三个小球上分别标记数字2,3,4.这六个小球除标记的数字外,其余完全相同.将A、B两个袋子中的小球摇匀,然后从A、B袋中各随机摸出一个小球,则摸出的这两个小球标记的数字之和为5的概率为______.
18.(2022·重庆江津·九年级期末)某农科所为了深入践行“绿水青山就是金山银山”的理念,大力开展对植物生长的研究,该农科所在相同条件下做某植物种子发芽率的试验,得到的结果如下表所示:
种子个数 100 200 300 400 500 600 700 800 900 1000 …
发芽种子个数 94 188 281 349 435 531 625 719 812 902 …
发芽种子频率 (结果保留两位小数) 0.94 0.94 0.94 0.87 0.87 0.89 0.89 0.90 0.90 0.90 …
根据频率的稳定性,估计这种植物种子不发芽的概率是______.
三、解答题
19.(2022·重庆梁平·九年级期末)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于多少;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
20.(2022·重庆开州·九年级期末)2021年8月,国务院教育督导委员会办公室印发《关于组织责任督学进行“五项管理”督导的通知》(简称通知),要求各省(区、市)教育督导部门,组织当地中小学校责任督学开展“五项管理”督导工作.为贯彻《通知》精神,开州区某学校团委组织了“手机管理”为主题的演讲比赛,根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图(其中A表示“一等奖”,B表示“二等奖”,C表示“三等奖”,D表示“优秀奖”).
请你根据统计图中所提供的信息解答下列问题:
(1)获奖总人数为 人, ;
(2)请将条形统计图补充完整;
(3)学校将从获得一等奖的4名同学(其中有一名男生,三名女姓)中随机抽取两名参加全市的比赛,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
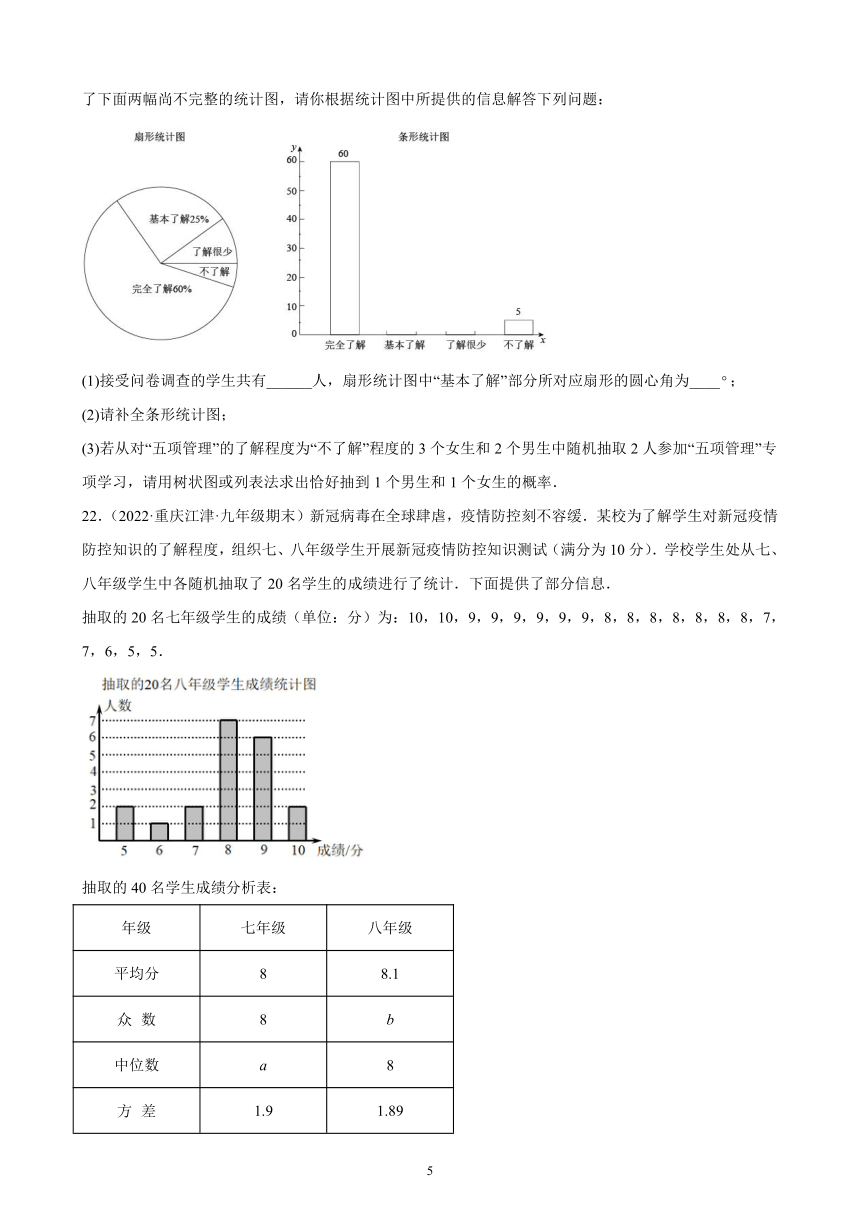
21.(2022·重庆万州·九年级期末)2021年1月以来,教育部相继出台文件,对加强中小学生手机、睡眠、读物、作业、体质管理(简称“五项管理”)做出部署,万州区各级各类学校坚决落实五项管理规定.某学校对部分学生就“五项管理”的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为____;
(2)请补全条形统计图;
(3)若从对“五项管理”的了解程度为“不了解”程度的3个女生和2个男生中随机抽取2人参加“五项管理”专项学习,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
22.(2022·重庆江津·九年级期末)新冠病毒在全球肆虐,疫情防控刻不容缓.某校为了解学生对新冠疫情防控知识的了解程度,组织七、八年级学生开展新冠疫情防控知识测试(满分为10分).学校学生处从七、八年级学生中各随机抽取了20名学生的成绩进行了统计.下面提供了部分信息.
抽取的20名七年级学生的成绩(单位:分)为:10,10,9,9,9,9,9,9,8,8,8,8,8,8,8,7,7,6,5,5.
抽取的40名学生成绩分析表:
年级 七年级 八年级
平均分 8 8.1
众 数 8 b
中位数 a 8
方 差 1.9 1.89
请根据以上信息,解答下列问题:
(1)直接写出上表中a,b的值;
(2)该校七、八年级共有学生2000人,估计此次测试成绩不低于9分的学生有多少人?
(3)在所抽取的七年级与八年级得10分的学生中,随机抽取2名学生在全校学生大会上进行新冠疫情防控知识宣讲,求所抽取的2名学生恰好是1名七年级学生和1名八年级学生的概率.
23.(2022·重庆南岸·九年级期末)如图,是一个智慧教育产品的展销厅的俯视示意图,小李进入展厅后,开始自由参观,每走到一个十字道口,他可能直行,也可能向左转成向右转,且这三种可能性均相同.
(1)求小李走进展厅的十字道口A后,向北走的概率;
(2)请用树状图或表格分析,小李到达第二个十字道口后向西方向参观的概率.
24.(2022·重庆渝中·九年级期末)从2021年开始,重庆市新高考采用“”模式:“3”指全国统考科目,即:语文、数学、外语三个学科为必选科目;“1”为首选科目,即:物理、历史这2个学科中任选1科,且必须选1科;“2”为再选科目,即:化学、生物、思想政治、地理这4个学科中任选2科,且必须选2科.小红在高一上期期末结束后,需要选择高考科目.
(1)小红在“首选科目”中,选择历史学科的概率是___________.
(2)用列表法或画树状图法,求小红在“再选科目”中选择思想政治和地理这两门学科的概率.
25.(2022·重庆黔江·九年级期末) A、B、C三人玩传花游戏,游戏规则是:第一次由A将花随机地传给B、C两人中的某一人,以后的每一次传花都是由上次的得花者随机地传给其他两人中的某一人.请你通过列表或画树状图,
(1)求第二次传花后,花在B手中的概率;
(2)求第三次传花后,花回到A手中的概率.
26.(2022·重庆潼南·九年级期末)一个不透明的盒子里装有5个黑球,2个白球和若干个黄球.它们除颜色不同外其余都相同,从中任意摸出1个球,是白球的概率为.
(1)求盒子里有几个黄球?
(2)小张和小王将盒子中的黑球取出4个,利用剩下的球进行摸球游戏.他们约定:先摸出1个球后不放回,再摸出1个球,若这两个球中有黄球,则小张胜,否则小王胜、你认为这个游戏公平吗?请用列表或画树状图说明理由.
参考答案:
1.C
【分析】用白球的个数除以球的总个数即为所求的概率.
【详解】解:因为一共有6个球,白球有4个,
所以从布袋里任意摸出1个球,摸到白球的概率为:.
故选C.
【点睛】本题考查了概率公式,用到的知识点为:概率等于所求情况数与总情况数之比.
2.B
【分析】根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.
【详解】解:观察这个图可知:黑色区域(5块)的面积占总面积(9块)的,
∴它最终停留在黑砖上的概率是.
故选:B.
【点睛】本题考查了几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
3.D
【分析】根据概率的意义分别判断后即可确定正确的选项.
【详解】解:A. 必然事件发生的概率是1,故该选项正确,不符合题意;
B. 不可能事件发生的概率是0,故该选项正确,不符合题意;
C. 随机事件发生的可能性越大,它的概率就越接近1,故该选项正确,不符合题意;
D. 概率很小的事件也可能发生,故该选项不正确,符合题意;
故选D
【点睛】本题考查概率的意义,理解概率的意义反映的只是这一事件发生的可能性的大小:必然发生的事件发生的概率为1,随机事件发生的概率大于0且小于1,不可能事件发生的概率为0.
4.A
【分析】指针转一圈360°,阴影部分的,占整个圆周的,根据概率公式计算即可.
【详解】解:指针指向阴影部分的概率是,
故选:A.
【点睛】本题考查简单的概率,是基础考点,难度较易,掌握相关知识是解题关键.
5.B
【分析】根据事件的确定性和不确定性,以及随机事件的含义和特征,逐项判断即可.
【详解】A.抛出的篮球会下落是必然事件,故此选项不符合题意;
B.经过有交通信号灯的路口,遇到红灯是随机事件,故此选项符合题意;
C.任意画一个三角形,其内角和是是不可能事件,故此选项不符合题意;
D. 400人中有两人的生日在同一天是必然事件,故此选项不符合题意;
故选B
【点睛】此题主要考查了事件的确定性和不确定性,要熟练掌握,解答此题的关键是要明确:事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件.
6.A
【分析】根据题意列表,然后根据表格即可求得所有等可能的结果数与两个指针同时落在偶数上的情况数,再根据概率公式求解即可求得答案.
【详解】解:列表得:
∴一共有25种等可能的结果,两个指针同时落在偶数上的有4种情况,
∴两个指针同时落在偶数上的概率是.
故选:A.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
7.C
【分析】画树状图,共有12种等可能的结果,其中使m+ n <0的结果有6种,再由概率公式求解即可
【详解】解:根据题意,画出树状图,如下图:
得到12种等可能结果,其中使的有6种,
∴使的概率为.
故选:C
【点睛】此题考查了列表法或树状图法求概率.正确画出树状图是解题的关键,用到的知识点为:概率=所求情况数与总情况数之比.
8.C
【分析】根据题意先由频率之和为1计算出白球的频率,再由数据总数×频率=频数计算白球的个数,即可求出答案.
【详解】解:∵摸到红色球、黑色球的频率稳定在15%和35%,
∴摸到白球的频率为1-15%-35%=50%,
故口袋中白色球的个数可能是40×50%=20(个).
故选:C.
【点睛】本题考查利用频率估计概率,大量反复试验下频率稳定值即概率.注意掌握频率=所求情况数与总情况数之比.
9.
【分析】根据题意列出图表得出所有等情况数和抽取的两张卡片上的字母相同的情况数,然后根据概率公式即可得出答案.
【详解】解:根据题意列表如下:
A B C
A AA BA CA
B AB BB CB
C AC BC CC
共有9种等可能的结果数,其中两次抽出的卡片上的字母相同的有3种情况,
所以P(抽取的两张卡片上的字母相同)==.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.
10.
【分析】画树状图列出所有等可能结果,从中找出符合条件的结果数,再根据概率公式求解即可.
【详解】解:画树状图如下:
由树状图可知,共有9种等可能结果,其中两次都摸到红球的有4种结果,
所以两次都摸到红球的概率为,
故答案为:.
【点睛】本题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
11.
【分析】画出树状图,由树状图求得所有等可能的结果与抽到的两张卡片上标有的数字之积为负数的结果,再由概率公式即可求得答案.
【详解】画树状图如图:
共有16个等可能的结果,两次抽取的卡片上的数字之积为负数的结果有4个,
∴两次抽取的卡片上的数字之积为负数的概率=.
故答案为:.
【点睛】本题考查了列表法与树状图法、概率公式,解答本题的关键是明确题意,画出相应的树状图,求出相应的概率.
12.##0.75
【分析】根据一元二次方程的定义,可得,根据一元二次方程的判别式的意义得到,可得,然后根据概率公式求解.
【详解】解:∵当且,一元二次方程有实数根
∴且
当a=0时,方程有实数根
从,0,1,2这四个数中任取一个数,符合条件的结果有,0
所得方程有实数根的概率为
故答案为:
【点睛】本题考查了列举法求概率,一元二次方程的定义,一元二次方程根的判别式,掌握以上知识是解题的关键.
13.
【详解】试题解析:列表:
第二次 第一次 0 10 20 30
0 -- 10 20 30
10 10 -- 30 40
20 20 30 -- 50
30 30 40 50 --
从上表可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,
因此P(不低于30元)=.
【点睛】本题主要考查用列表法或树状图求概率.解决本题的关键是弄清题意,满200元可以摸两次,但摸出一个后不放回,概率在变化.用到的知识点为:概率=所求情况数与总情况数之比.
14.
【分析】结合题意,根据列举法求概率,即可得到答案.
【详解】根据题意,将2本艺术类、4本文学类、6本科技类的书籍混在一起,随机抽取一本,共12种情况,其中抽中文学类共4种情况;
∴抽中文学类的概率为:
故答案为:.
【点睛】本题考查了概率的知识;结果的关键是熟练掌握列举法求概率的性质,从而完成求解.
15.
【分析】根据二次函数的性质,对称轴为,进而可得同号,根据列表法即可求得二次函数的对称轴在轴左侧的概率
【详解】解:二次函数的对称轴在轴左侧
对称轴为,即同号,
列表如下
共有12种等可能结果,其中同号的结果有4种
则二次函数的对称轴在轴左侧的概率为
故答案为:
【点睛】本题考查了二次函数图象的性质,列表法求概率,掌握二次函数的图象与系数的关系以及列表法求概率是解题的关键.
16.
【分析】根据题意可以写出所有的可能性,从而可以得到可能性,进而求得概率.
【详解】解:由题意可得,
从袋子中随机抽取一个小球,记标号为,放回后将袋子摇匀,再随机抽取一个小球,记标号为,共9种情况,
满足可能性为:,,,,,
满足的概率为:.
故答案为:
【点睛】本题考查列表法和树状图法、不等式,解题的关键是明确题意,求出相应的概率.
17.
【分析】先列表,再利用表格信息得到所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
【详解】解:列表如下:
1 2 3
2 1+2=3 2+2=4 2+3=5
3 3+1=4 3+2=5 3+3=6
4 4+1=5 4+2=6 4+3=7
可得:所有的等可能的结果数有9种,而和为5的结果数有3种,
摸出的这两个小球标记的数字之和为5的概率为:
故答案为:
【点睛】本题考查的是利用列表法或画树状图的方法求解简单随机事件的概率,掌握“列表或画树状图的方法”是解本题的关键.
18.0.1
【分析】大量重复试验下“发芽种子”的频率可以估计“发芽种子”的概率,据此求解.
【详解】观察表格发现随着实验次数的增多频率逐渐稳定在0.9附近,
故“发芽种子”的概率估计值为0.9.
∴这种植物种子不发芽的概率是0.1.
故答案为:0.1.
【点睛】本题考查了利用频率估计概率的知识,解题的关键是了解大量重复试验中某个事件发生的频率能估计概率.
19.(1);(2).
【分析】(1)根据概率公式直接填即可;
(2)依据题意分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
【详解】解:(1)有4个开关,只有D开关一个闭合小灯发亮,
所以任意闭合其中一个开关,则小灯泡发光的概率是;
(2)画树状图如右图:
结果任意闭合其中两个开关的情况共有12种,
其中能使小灯泡发光的情况有6种,
小灯泡发光的概率是.
【点睛】本题考查的知识点是概率的求法,解题关键是熟记概率=所求情况数与总情况数之比.
20.(1)40,30
(2)见解析
(3)
【分析】(1)用“二等奖”人数除以它所占的百分比得到获奖总人数,然后计算“三等奖”人数所占的百分比得到m的值;
(2)利用“三等奖”人数为12补全条形统计图;
(3)画树状图展示所有12种等可能的结果,找出抽取同学中恰有一名男生和一名女生的结果数,然后根据概率公式求解.
(1)
解:获奖总人数为8÷20%=40(人),
m%=×100%=30%,
即m=30;
故答案为40;30;
(2)
解:“三等奖”人数为40-4-8-16=12(人),
条形统计图补充为:
(3)
解:画树状图为:
共有12种等可能的结果,抽取同学中恰有一名男生和一名女生的结果数为6,
所以抽取同学中恰有一名男生和一名女生的概率==.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.
21.(1);
(2)见解析
(3)
【分析】(1)根据扇形统计图中“完全了解”的占比为60%,图形统计图中“完全了解”的人数为60人,用60除以60%即可求得总人数,根据“基本了解”的占比为25%,用25%乘以360°即可求得扇形统计图中“基本了解”部分所对应扇形的圆心角的度数;
(2)根据总人数乘以25%即可求得“基本了解”的人数,进而根据总人数减去“完全了解”, “基本了解”和“不了解”的人数即可求得“了解很少”的人数,进而补全统计图;
(3)根据列表法求概率即可.
(1)
接受问卷调查的学生共有(人),
故答案为:;
(2)
“基本了解”的人数为:(人)
“了解很少”的人数为:(人)
补全统计图如下,
(3)
设3个女生分别为,两个男生分别为
列表如下
共有20种等可能情形,其中一男一女的情形有12种,
恰好抽到1个男生和1个女生的概率为
【点睛】本题考查了根据样本求总体,求扇形统计图的圆心角的度数,求条形统计图中某一项,列表法求概率,从统计图中获取信息是解题的关键.
22.(1)
(2)
(3)
【分析】(1)根据众数和中位数的概念求解可得;
(2)用总人数乘以样本中七、八年级不低于9分的学生人数和所占比例即可得,
(3)根据列表法求概率即可.
(1)
根据抽取的20名七年级学生的成绩找到第10个和第11个成绩都是8,则中位数为8,即,
根据条形统计图可知9分的有6人,人数最多,则众数为9,即
(2)
解:∵此次测试成绩不低于9分的七年级学生有8人,八年级学生有9人
∴此次测试成绩不低于9分的学生有(人)
(3)
解:∵七年级得10分的有2人,八年级得10分的有3人
设七年级的2人分别为,八年级的3人分别
列表如下,
根据列表可知,共有20种等可能结果,其中1名七年级学生和1名八年级学生的情形有12钟
则所抽取的2名学生恰好是1名七年级学生和1名八年级学生的概率为
【点睛】本题考查了求中位数,众数,根据样本估计总体,列表法求概率,掌握以上知识是解题的关键.
23.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画出树状图,共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,由概率公式求解即可.
(1)
小李走到十字道口A向北走的概率为;
(2)
画树状图如下:
共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,
∴向西参观的概率为.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
24.(1)
(2)
【分析】(1)根据概率的公式计算可得答案;
(2)画树状图,共有12个等可能的结果,该同学恰好选中思想政治和地理化两科的结果有2个,再由概率公式求解即可.
(1)
解:选择物理、历史共有2中等可能结果,选择历史学科的结果有1种,所以选择历史学科的概率是;
(2)
假设A表示化学、B表示生物、C表示思想政治、D表示地理,画树状图如下图:
共有12个等可能的结果,该同学恰好选中思想政治和地理的结果有2个,所以该同学恰好选中思想政治和地理的概率为.
【点睛】此题考查了概率的求法,利用如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,还考查了用列表法或树状图法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,做题的关键是掌握概率的求法.
25.(1)
(2)
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次传花后,花恰在B手中的情况,再利用概率公式即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与三次传花后,花恰在A手中的情况,再利用概率公式即可求得答案.
(1)
解:画树状图得:
∵共有4种等可能的结果,两次传花后,花恰在B手中的只有1种情况,
∴两次传花后,花恰在B手中的概率为:;
(2)
解:画树状图得:
∵共有8种等可能的结果,三次传花后,花恰在手中的有2种情况,
∴三次传花后,花恰在手中的概率为:.
【点睛】本题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
26.(1)布袋里有1个黄球
(2)公平,表格见解析
【分析】(1)设布袋里黄球有x个,根据“白球的概率为”可得关于x的分式方程,解之可得答案;
(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
(1)
解:设布袋里黄球有x个,
根据题意,得:,
解得:x=1,
经检验:x=1是原分式方程的解,
所以布袋里有1个黄球;
(2)
解:公平;
列表如下:
白 白 黑 黄
白 (白,白) (白,黑) (白,黄)
白 (白,白) (白,黑) (白,黄)
黑 (黑,白) (黑,白) (黑,黄)
黄 (黄,白) (黄,白) (黄,黑)
由表知,共有12种等可能结果,其中两个球中有黄球的有6种情况,两个球中没有黄球的有6种情况,
∴P(小张胜)=P(小王胜)= ,
∴这个游戏公平.
【点睛】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
一、单选题
1.(2022·重庆永川·九年级期末)一个布袋里装有6个只有颜色不同的球,其中2个红球,4个白球.从布袋里任意摸出1个球,则摸出的球是白球的概率为( )
A. B. C. D.
2.(2022·重庆梁平·九年级期末)一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上.如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是( )
A. B. C. D.
3.(2022·重庆渝中·九年级期末)下列说法错误的是( )
A.必然事件发生的概率是1 B.不可能事件发生的概率为0
C.随机事件发生的可能性越大,它的概率就越接近1 D.概率很小的事件不可能发生
4.(2022·重庆綦江·九年级期末)图2是由图1的窗户抽象出来的平面图形,半圆的直径与长方形的宽相等,此平面图形的对称轴与半圆的直径将图形分成四个部分,半圆的圆心点处有一任意转动指针,指针停止的位置是等可能的,则指针指向阴影部分的概率是( )
A. B.
C. D.因为长方形的长未知,所以概率不确定
5.(2022·重庆云阳·九年级期末)下列事件是随机事件的是( )
A.抛出的篮球会下落
B.经过有交通信号灯的路口,遇到红灯
C.任意画一个三角形,其内角和是
D.400人中有两人的生日在同一天
6.(2022·重庆梁平·九年级期末)如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,两个指针同时落在偶数上的概率是( ).
A. B. C. D.
7.(2022·重庆九龙坡·九年级期末)有4张正面分别标有数字、、0、3的卡片,它们除数字不同外其余全部相同.先将它们背面朝上,洗匀后从中随机抽取一张,得到的数记为m,不放回,再从剩余卡片中随机抽取一张,得到的数记为n,则使的概率为( )
A. B. C. D.
8.(2022·重庆黔江·九年级期末)在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率分别稳定在15%和35%,则口袋中白色球的个数可能是( )
A.6个 B.14个 C.20个 D.40个
二、填空题
9.(2022·重庆·中考真题)有三张完全一样正面分别写有字母A,B,C的卡片.将其背面朝上并洗匀,从中随机抽取一张,记下卡片上的字母后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的字母相同的概率是_________.
10.(2022·重庆·中考真题)不透明的袋子中装有个红球和个白球,除颜色外无其他差别,随机摸出一个球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率是________.
11.(2022·重庆市武隆区江口中学校九年级期末)在桌面上放有四张背面完全一样的卡片.卡片的正面分别标有数字﹣1,0,1,3.把四张卡片背面朝上,随机抽取一张,记下数字且放回洗匀,再从中随机抽取一张.则两次抽取卡片上的数字之积为负数的概率是_______.
12.(2022·重庆渝中·九年级期末)从,0,1,2这四个数中任取一个数,作为关于x的方程中a的值,则该方程有实数根的概率为_________.
13.(2022·重庆梁平·九年级期末)某商店设计了一种促销活动来吸引顾客:在一个不透明的箱子里放有个相同的乒乓球,乒乓球上分别标有“元”、“元”、“元”、“元”的字样.规定:顾客在本超市一次性消费满元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费元,则该顾客所获得购物券的金额不低于元的概率是________.
14.(2022·重庆开州·九年级期末)将2本艺术类、4本文学类、6本科技类的书籍混在一起.若小陈从中随机抽取一本,则抽中文学类的概率为__________.
15.(2022·重庆巴蜀中学九年级期末)有四张完全相同的卡片,正面分别标有数字,,,,将四张卡片背面朝上,任抽一张卡片,卡片上的数字记为,再从剩下卡片中抽一张,卡片上的数字记为,则二次函数的对称轴在轴左侧的概率是__________.
16.(2022·重庆南开中学九年级期末)在一个不透明的口袋里装有除标号外完全一样的三个小球,小球上分别标有2,﹣1,3这三个数字,从袋中随机摸出一个小球,记标号为a,然后放回摇匀后再随机摸出一个小球,记标号为b,则满足的概率是______.
17.(2022·重庆八中九年级期末)现有A、B两个不透明的袋子,各装有三个小球,A袋中的三个小球上分别标记数字1,2,3;B袋中的三个小球上分别标记数字2,3,4.这六个小球除标记的数字外,其余完全相同.将A、B两个袋子中的小球摇匀,然后从A、B袋中各随机摸出一个小球,则摸出的这两个小球标记的数字之和为5的概率为______.
18.(2022·重庆江津·九年级期末)某农科所为了深入践行“绿水青山就是金山银山”的理念,大力开展对植物生长的研究,该农科所在相同条件下做某植物种子发芽率的试验,得到的结果如下表所示:
种子个数 100 200 300 400 500 600 700 800 900 1000 …
发芽种子个数 94 188 281 349 435 531 625 719 812 902 …
发芽种子频率 (结果保留两位小数) 0.94 0.94 0.94 0.87 0.87 0.89 0.89 0.90 0.90 0.90 …
根据频率的稳定性,估计这种植物种子不发芽的概率是______.
三、解答题
19.(2022·重庆梁平·九年级期末)如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于多少;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
20.(2022·重庆开州·九年级期末)2021年8月,国务院教育督导委员会办公室印发《关于组织责任督学进行“五项管理”督导的通知》(简称通知),要求各省(区、市)教育督导部门,组织当地中小学校责任督学开展“五项管理”督导工作.为贯彻《通知》精神,开州区某学校团委组织了“手机管理”为主题的演讲比赛,根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图(其中A表示“一等奖”,B表示“二等奖”,C表示“三等奖”,D表示“优秀奖”).
请你根据统计图中所提供的信息解答下列问题:
(1)获奖总人数为 人, ;
(2)请将条形统计图补充完整;
(3)学校将从获得一等奖的4名同学(其中有一名男生,三名女姓)中随机抽取两名参加全市的比赛,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.
21.(2022·重庆万州·九年级期末)2021年1月以来,教育部相继出台文件,对加强中小学生手机、睡眠、读物、作业、体质管理(简称“五项管理”)做出部署,万州区各级各类学校坚决落实五项管理规定.某学校对部分学生就“五项管理”的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为____;
(2)请补全条形统计图;
(3)若从对“五项管理”的了解程度为“不了解”程度的3个女生和2个男生中随机抽取2人参加“五项管理”专项学习,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
22.(2022·重庆江津·九年级期末)新冠病毒在全球肆虐,疫情防控刻不容缓.某校为了解学生对新冠疫情防控知识的了解程度,组织七、八年级学生开展新冠疫情防控知识测试(满分为10分).学校学生处从七、八年级学生中各随机抽取了20名学生的成绩进行了统计.下面提供了部分信息.
抽取的20名七年级学生的成绩(单位:分)为:10,10,9,9,9,9,9,9,8,8,8,8,8,8,8,7,7,6,5,5.
抽取的40名学生成绩分析表:
年级 七年级 八年级
平均分 8 8.1
众 数 8 b
中位数 a 8
方 差 1.9 1.89
请根据以上信息,解答下列问题:
(1)直接写出上表中a,b的值;
(2)该校七、八年级共有学生2000人,估计此次测试成绩不低于9分的学生有多少人?
(3)在所抽取的七年级与八年级得10分的学生中,随机抽取2名学生在全校学生大会上进行新冠疫情防控知识宣讲,求所抽取的2名学生恰好是1名七年级学生和1名八年级学生的概率.
23.(2022·重庆南岸·九年级期末)如图,是一个智慧教育产品的展销厅的俯视示意图,小李进入展厅后,开始自由参观,每走到一个十字道口,他可能直行,也可能向左转成向右转,且这三种可能性均相同.
(1)求小李走进展厅的十字道口A后,向北走的概率;
(2)请用树状图或表格分析,小李到达第二个十字道口后向西方向参观的概率.
24.(2022·重庆渝中·九年级期末)从2021年开始,重庆市新高考采用“”模式:“3”指全国统考科目,即:语文、数学、外语三个学科为必选科目;“1”为首选科目,即:物理、历史这2个学科中任选1科,且必须选1科;“2”为再选科目,即:化学、生物、思想政治、地理这4个学科中任选2科,且必须选2科.小红在高一上期期末结束后,需要选择高考科目.
(1)小红在“首选科目”中,选择历史学科的概率是___________.
(2)用列表法或画树状图法,求小红在“再选科目”中选择思想政治和地理这两门学科的概率.
25.(2022·重庆黔江·九年级期末) A、B、C三人玩传花游戏,游戏规则是:第一次由A将花随机地传给B、C两人中的某一人,以后的每一次传花都是由上次的得花者随机地传给其他两人中的某一人.请你通过列表或画树状图,
(1)求第二次传花后,花在B手中的概率;
(2)求第三次传花后,花回到A手中的概率.
26.(2022·重庆潼南·九年级期末)一个不透明的盒子里装有5个黑球,2个白球和若干个黄球.它们除颜色不同外其余都相同,从中任意摸出1个球,是白球的概率为.
(1)求盒子里有几个黄球?
(2)小张和小王将盒子中的黑球取出4个,利用剩下的球进行摸球游戏.他们约定:先摸出1个球后不放回,再摸出1个球,若这两个球中有黄球,则小张胜,否则小王胜、你认为这个游戏公平吗?请用列表或画树状图说明理由.
参考答案:
1.C
【分析】用白球的个数除以球的总个数即为所求的概率.
【详解】解:因为一共有6个球,白球有4个,
所以从布袋里任意摸出1个球,摸到白球的概率为:.
故选C.
【点睛】本题考查了概率公式,用到的知识点为:概率等于所求情况数与总情况数之比.
2.B
【分析】根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.
【详解】解:观察这个图可知:黑色区域(5块)的面积占总面积(9块)的,
∴它最终停留在黑砖上的概率是.
故选:B.
【点睛】本题考查了几何概率的求法:首先根据题意将代数关系用面积表示出来,一般用阴影区域表示所求事件(A);然后计算阴影区域的面积在总面积中占的比例,这个比例即事件(A)发生的概率.
3.D
【分析】根据概率的意义分别判断后即可确定正确的选项.
【详解】解:A. 必然事件发生的概率是1,故该选项正确,不符合题意;
B. 不可能事件发生的概率是0,故该选项正确,不符合题意;
C. 随机事件发生的可能性越大,它的概率就越接近1,故该选项正确,不符合题意;
D. 概率很小的事件也可能发生,故该选项不正确,符合题意;
故选D
【点睛】本题考查概率的意义,理解概率的意义反映的只是这一事件发生的可能性的大小:必然发生的事件发生的概率为1,随机事件发生的概率大于0且小于1,不可能事件发生的概率为0.
4.A
【分析】指针转一圈360°,阴影部分的,占整个圆周的,根据概率公式计算即可.
【详解】解:指针指向阴影部分的概率是,
故选:A.
【点睛】本题考查简单的概率,是基础考点,难度较易,掌握相关知识是解题关键.
5.B
【分析】根据事件的确定性和不确定性,以及随机事件的含义和特征,逐项判断即可.
【详解】A.抛出的篮球会下落是必然事件,故此选项不符合题意;
B.经过有交通信号灯的路口,遇到红灯是随机事件,故此选项符合题意;
C.任意画一个三角形,其内角和是是不可能事件,故此选项不符合题意;
D. 400人中有两人的生日在同一天是必然事件,故此选项不符合题意;
故选B
【点睛】此题主要考查了事件的确定性和不确定性,要熟练掌握,解答此题的关键是要明确:事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件.
6.A
【分析】根据题意列表,然后根据表格即可求得所有等可能的结果数与两个指针同时落在偶数上的情况数,再根据概率公式求解即可求得答案.
【详解】解:列表得:
∴一共有25种等可能的结果,两个指针同时落在偶数上的有4种情况,
∴两个指针同时落在偶数上的概率是.
故选:A.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
7.C
【分析】画树状图,共有12种等可能的结果,其中使m+ n <0的结果有6种,再由概率公式求解即可
【详解】解:根据题意,画出树状图,如下图:
得到12种等可能结果,其中使的有6种,
∴使的概率为.
故选:C
【点睛】此题考查了列表法或树状图法求概率.正确画出树状图是解题的关键,用到的知识点为:概率=所求情况数与总情况数之比.
8.C
【分析】根据题意先由频率之和为1计算出白球的频率,再由数据总数×频率=频数计算白球的个数,即可求出答案.
【详解】解:∵摸到红色球、黑色球的频率稳定在15%和35%,
∴摸到白球的频率为1-15%-35%=50%,
故口袋中白色球的个数可能是40×50%=20(个).
故选:C.
【点睛】本题考查利用频率估计概率,大量反复试验下频率稳定值即概率.注意掌握频率=所求情况数与总情况数之比.
9.
【分析】根据题意列出图表得出所有等情况数和抽取的两张卡片上的字母相同的情况数,然后根据概率公式即可得出答案.
【详解】解:根据题意列表如下:
A B C
A AA BA CA
B AB BB CB
C AC BC CC
共有9种等可能的结果数,其中两次抽出的卡片上的字母相同的有3种情况,
所以P(抽取的两张卡片上的字母相同)==.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.
10.
【分析】画树状图列出所有等可能结果,从中找出符合条件的结果数,再根据概率公式求解即可.
【详解】解:画树状图如下:
由树状图可知,共有9种等可能结果,其中两次都摸到红球的有4种结果,
所以两次都摸到红球的概率为,
故答案为:.
【点睛】本题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
11.
【分析】画出树状图,由树状图求得所有等可能的结果与抽到的两张卡片上标有的数字之积为负数的结果,再由概率公式即可求得答案.
【详解】画树状图如图:
共有16个等可能的结果,两次抽取的卡片上的数字之积为负数的结果有4个,
∴两次抽取的卡片上的数字之积为负数的概率=.
故答案为:.
【点睛】本题考查了列表法与树状图法、概率公式,解答本题的关键是明确题意,画出相应的树状图,求出相应的概率.
12.##0.75
【分析】根据一元二次方程的定义,可得,根据一元二次方程的判别式的意义得到,可得,然后根据概率公式求解.
【详解】解:∵当且,一元二次方程有实数根
∴且
当a=0时,方程有实数根
从,0,1,2这四个数中任取一个数,符合条件的结果有,0
所得方程有实数根的概率为
故答案为:
【点睛】本题考查了列举法求概率,一元二次方程的定义,一元二次方程根的判别式,掌握以上知识是解题的关键.
13.
【详解】试题解析:列表:
第二次 第一次 0 10 20 30
0 -- 10 20 30
10 10 -- 30 40
20 20 30 -- 50
30 30 40 50 --
从上表可以看出,共有12种可能结果,其中大于或等于30元共有8种可能结果,
因此P(不低于30元)=.
【点睛】本题主要考查用列表法或树状图求概率.解决本题的关键是弄清题意,满200元可以摸两次,但摸出一个后不放回,概率在变化.用到的知识点为:概率=所求情况数与总情况数之比.
14.
【分析】结合题意,根据列举法求概率,即可得到答案.
【详解】根据题意,将2本艺术类、4本文学类、6本科技类的书籍混在一起,随机抽取一本,共12种情况,其中抽中文学类共4种情况;
∴抽中文学类的概率为:
故答案为:.
【点睛】本题考查了概率的知识;结果的关键是熟练掌握列举法求概率的性质,从而完成求解.
15.
【分析】根据二次函数的性质,对称轴为,进而可得同号,根据列表法即可求得二次函数的对称轴在轴左侧的概率
【详解】解:二次函数的对称轴在轴左侧
对称轴为,即同号,
列表如下
共有12种等可能结果,其中同号的结果有4种
则二次函数的对称轴在轴左侧的概率为
故答案为:
【点睛】本题考查了二次函数图象的性质,列表法求概率,掌握二次函数的图象与系数的关系以及列表法求概率是解题的关键.
16.
【分析】根据题意可以写出所有的可能性,从而可以得到可能性,进而求得概率.
【详解】解:由题意可得,
从袋子中随机抽取一个小球,记标号为,放回后将袋子摇匀,再随机抽取一个小球,记标号为,共9种情况,
满足可能性为:,,,,,
满足的概率为:.
故答案为:
【点睛】本题考查列表法和树状图法、不等式,解题的关键是明确题意,求出相应的概率.
17.
【分析】先列表,再利用表格信息得到所有的等可能的结果数与符合条件的结果数,再利用概率公式进行计算即可.
【详解】解:列表如下:
1 2 3
2 1+2=3 2+2=4 2+3=5
3 3+1=4 3+2=5 3+3=6
4 4+1=5 4+2=6 4+3=7
可得:所有的等可能的结果数有9种,而和为5的结果数有3种,
摸出的这两个小球标记的数字之和为5的概率为:
故答案为:
【点睛】本题考查的是利用列表法或画树状图的方法求解简单随机事件的概率,掌握“列表或画树状图的方法”是解本题的关键.
18.0.1
【分析】大量重复试验下“发芽种子”的频率可以估计“发芽种子”的概率,据此求解.
【详解】观察表格发现随着实验次数的增多频率逐渐稳定在0.9附近,
故“发芽种子”的概率估计值为0.9.
∴这种植物种子不发芽的概率是0.1.
故答案为:0.1.
【点睛】本题考查了利用频率估计概率的知识,解题的关键是了解大量重复试验中某个事件发生的频率能估计概率.
19.(1);(2).
【分析】(1)根据概率公式直接填即可;
(2)依据题意分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
【详解】解:(1)有4个开关,只有D开关一个闭合小灯发亮,
所以任意闭合其中一个开关,则小灯泡发光的概率是;
(2)画树状图如右图:
结果任意闭合其中两个开关的情况共有12种,
其中能使小灯泡发光的情况有6种,
小灯泡发光的概率是.
【点睛】本题考查的知识点是概率的求法,解题关键是熟记概率=所求情况数与总情况数之比.
20.(1)40,30
(2)见解析
(3)
【分析】(1)用“二等奖”人数除以它所占的百分比得到获奖总人数,然后计算“三等奖”人数所占的百分比得到m的值;
(2)利用“三等奖”人数为12补全条形统计图;
(3)画树状图展示所有12种等可能的结果,找出抽取同学中恰有一名男生和一名女生的结果数,然后根据概率公式求解.
(1)
解:获奖总人数为8÷20%=40(人),
m%=×100%=30%,
即m=30;
故答案为40;30;
(2)
解:“三等奖”人数为40-4-8-16=12(人),
条形统计图补充为:
(3)
解:画树状图为:
共有12种等可能的结果,抽取同学中恰有一名男生和一名女生的结果数为6,
所以抽取同学中恰有一名男生和一名女生的概率==.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.
21.(1);
(2)见解析
(3)
【分析】(1)根据扇形统计图中“完全了解”的占比为60%,图形统计图中“完全了解”的人数为60人,用60除以60%即可求得总人数,根据“基本了解”的占比为25%,用25%乘以360°即可求得扇形统计图中“基本了解”部分所对应扇形的圆心角的度数;
(2)根据总人数乘以25%即可求得“基本了解”的人数,进而根据总人数减去“完全了解”, “基本了解”和“不了解”的人数即可求得“了解很少”的人数,进而补全统计图;
(3)根据列表法求概率即可.
(1)
接受问卷调查的学生共有(人),
故答案为:;
(2)
“基本了解”的人数为:(人)
“了解很少”的人数为:(人)
补全统计图如下,
(3)
设3个女生分别为,两个男生分别为
列表如下
共有20种等可能情形,其中一男一女的情形有12种,
恰好抽到1个男生和1个女生的概率为
【点睛】本题考查了根据样本求总体,求扇形统计图的圆心角的度数,求条形统计图中某一项,列表法求概率,从统计图中获取信息是解题的关键.
22.(1)
(2)
(3)
【分析】(1)根据众数和中位数的概念求解可得;
(2)用总人数乘以样本中七、八年级不低于9分的学生人数和所占比例即可得,
(3)根据列表法求概率即可.
(1)
根据抽取的20名七年级学生的成绩找到第10个和第11个成绩都是8,则中位数为8,即,
根据条形统计图可知9分的有6人,人数最多,则众数为9,即
(2)
解:∵此次测试成绩不低于9分的七年级学生有8人,八年级学生有9人
∴此次测试成绩不低于9分的学生有(人)
(3)
解:∵七年级得10分的有2人,八年级得10分的有3人
设七年级的2人分别为,八年级的3人分别
列表如下,
根据列表可知,共有20种等可能结果,其中1名七年级学生和1名八年级学生的情形有12钟
则所抽取的2名学生恰好是1名七年级学生和1名八年级学生的概率为
【点睛】本题考查了求中位数,众数,根据样本估计总体,列表法求概率,掌握以上知识是解题的关键.
23.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画出树状图,共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,由概率公式求解即可.
(1)
小李走到十字道口A向北走的概率为;
(2)
画树状图如下:
共有9种等可能的结果,小李经过两个十字道口后向西参观的结果有3种,向南参观的结果有2种,向北参观的结果有2种,向东参观的结果有2种,
∴向西参观的概率为.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.
24.(1)
(2)
【分析】(1)根据概率的公式计算可得答案;
(2)画树状图,共有12个等可能的结果,该同学恰好选中思想政治和地理化两科的结果有2个,再由概率公式求解即可.
(1)
解:选择物理、历史共有2中等可能结果,选择历史学科的结果有1种,所以选择历史学科的概率是;
(2)
假设A表示化学、B表示生物、C表示思想政治、D表示地理,画树状图如下图:
共有12个等可能的结果,该同学恰好选中思想政治和地理的结果有2个,所以该同学恰好选中思想政治和地理的概率为.
【点睛】此题考查了概率的求法,利用如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,还考查了用列表法或树状图法求概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,做题的关键是掌握概率的求法.
25.(1)
(2)
【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次传花后,花恰在B手中的情况,再利用概率公式即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与三次传花后,花恰在A手中的情况,再利用概率公式即可求得答案.
(1)
解:画树状图得:
∵共有4种等可能的结果,两次传花后,花恰在B手中的只有1种情况,
∴两次传花后,花恰在B手中的概率为:;
(2)
解:画树状图得:
∵共有8种等可能的结果,三次传花后,花恰在手中的有2种情况,
∴三次传花后,花恰在手中的概率为:.
【点睛】本题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
26.(1)布袋里有1个黄球
(2)公平,表格见解析
【分析】(1)设布袋里黄球有x个,根据“白球的概率为”可得关于x的分式方程,解之可得答案;
(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
(1)
解:设布袋里黄球有x个,
根据题意,得:,
解得:x=1,
经检验:x=1是原分式方程的解,
所以布袋里有1个黄球;
(2)
解:公平;
列表如下:
白 白 黑 黄
白 (白,白) (白,黑) (白,黄)
白 (白,白) (白,黑) (白,黄)
黑 (黑,白) (黑,白) (黑,黄)
黄 (黄,白) (黄,白) (黄,黑)
由表知,共有12种等可能结果,其中两个球中有黄球的有6种情况,两个球中没有黄球的有6种情况,
∴P(小张胜)=P(小王胜)= ,
∴这个游戏公平.
【点睛】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
同课章节目录
