人教A版(2019)高中数学必修第二册 第十章《概率---章末复习》名师课件(共28张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 第十章《概率---章末复习》名师课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 09:04:15 | ||
图片预览








文档简介
(共28张PPT)
人教A版同步教材名师课件
概率
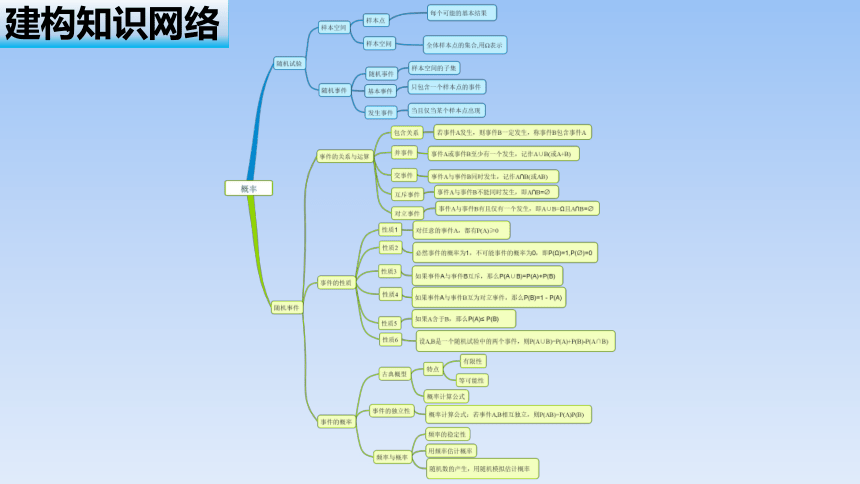
建构知识网络
洞悉高考
专题分布 考点频次 考试分值 命题热点
了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别 ★★ 5年18考 学考赋分 5~10分 【内容特点】利用频率估计概率;求古典概型的概率,求几何概型的概率,古典概型与统计的综合问题
【题型形式】以选择题、填空题、解答题.
如2017·江苏·T3,2018·全国I·T19,全国卷Ⅱ·理·T10,2018·北京·T17,2018·江苏·T7,2018·天津·T15.
了解两个互斥事件的概率加法公式 ★★ 5年18考
了解事件的相互独立性 ★★ 5年18考
理解古典概型及其概率计算公式 ★★ 5年24考 高考赋分 5~12分
会用列举法计算一些随机事件所含的样本,点个数及事件发生的概率 ★★ 5年24考
了解随机数的意义,能运用随机模拟的方法估计概率 ★★★ 5年36考
知识归纳
随机事件主要包括三个方面的内容:有限样本空间、事件的关系和运算、概率的基本性质.
1. 对于有限样本空间,要紧紧抓住随机试验的三个特点和样本空间的概念,正确列出样本空间,为后面解决古典概型打下良好的基础.
2. 关于事件的关系和运算,类比集合的相关运算法则,重点区分互斥事件和对立事件.
一、随机事件
知识归纳
3. 关于概率的六条基本性质,其中互斥事件的概率之和与对立事件的概率之差仍是我们求概率运算的主体.对于性质6;设A,B是一个随机试验中的两个事件,有
要引起高度的注意,注意其使用的条件.
4. 应用互斥事件的概率的加法公式解题时,一定要注意首先各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于复杂事件的概率,可以转化为求其对立事件的概率.主要考查角度:(1)事件的样本空间;(2)事件关系的判定; (3)互斥事件与对立事件的概率.
一、随机事件
例1、2021年某省新高考将实行“3+1+2”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件A:“他选择政治和地理”,事件B:“他选择化学和地理”,则事件A与事件B ( )
A.是互斥事件,但不是对立事件 B.是对立事件,但不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件,也不是对立事件
事件A:“他选择政治和地理”,事件B:“他选择化学和地理”,则事件A与事件B不能同时发生,但能同时不发生,故事件A和事件B是互斥事件,但不是对立事件.
解析
一、随机事件
典例讲解
例2、某商场有奖销售中,每购物满100元可抽取1张奖券,多购多得,每1000张奖券为一个开奖单位.设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为求:
;
抽取1张奖券中奖的概率;
抽取1张奖券不中特等奖或一等奖的概率
对于(1)直接求解;对于(2)(3)应明确要求事件中包含哪些事件.
解析
一、随机事件
典例讲解
一、随机事件
解
由题意知,事件为互斥事件.
(1)每1000张奖券中设特等奖1个,一等奖10个,二等奖50个,
(2) 设“抽取1张奖券中奖”为事件D,则
(3) 设“抽取1张奖券不中特等奖或一等奖”为事件E
典例讲解
知识归纳
1. 古典概型是一种最基本的概型,也是学习其他概型的基础,解决这类问题要紧紧抓住古典概型的两个基本特征,即有限性和等可能性.
2. 对古典概型概率的计算,关键是分清样本空间包含个样本点,事件A包含其中的个样本点,有时需要用列举法把样本空间一一列举出来,再利用公式求出事件的概率,这是一个形象、直观的好方法,但列举时必须按某一顺序做到不重复、不遗漏.
主要考查角度:古典概型的概率求解.
二、古典概型的概率求解
例3、某购物中心举行抽奖活动,顾客从装有编号分别为 四个球的抽奖箱中,每次取出1个球,记下编号后放回,连续取两次(假设取到任何一个小球的可能性相同).若取出的两个小球号码相加之和等于5,则中一等奖;若取出的两个小球号码相加之和等于4,则中二等奖;若取出的两个小球号码相加之和等于3,则中三等奖;其他情况不中奖.
(1)求顾客中三等奖的概率;(2)求顾客未中奖的概率.
根据题目条件,列出样本空间,然后按照古典概型和概率的性质进行求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)设事件A为“顾客中三等奖”,所有样本点包括
所以顾客中三等奖的概率为
典例讲解
二、古典概型的概率求解
解
(2)设事件B为“顾客未中奖”,
“两个小球号码相加之和等于5”这一事件包括样本点(2,3),(3,2),共2个.
“两个小球号码相加之和等于4”这一事件包括样本点
所以
所以顾客未中奖的概率为
典例讲解
例4、已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(i i )设为事件“抽取的2名同学来自同一年级”,求事件发生的概率.
根据分层抽样的方法确定从甲、乙、丙三个年级的学生志愿者中分别抽取的人数,然后按照要求列出样本空间,进行概率求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人、2人、2人.
(2)(i)从抽出的7名同学中随机抽取2名同学的所有可能结果为
,共21种.
(ii)由(1),不妨设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为 共5种.所以事件 发生的概率
典例讲解
例5、2021年福建省高考实行“3+1+2” 模式.“3+1+2”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
(1)若学生甲在“1”中选物理,在“2”中任选2科,求学生甲选化学和生物的概率;(2)若学生乙在“1”中任选1科,在“2”中任选2科,求学生乙不选政治但选生物的概率.
对于(1)(2)两问,由于各自要求的条件不一样,需要各自列出样本空间,然后找出发生事件,从而按照古典概型的概率公式求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)记“学生甲选化学和生物”为事件A
学生甲在“1”中选物理,在“2”中任选2科的样本点有:(生,化),(生,政),(生,地),(化,政),(化,地),(政,地),共6个.
事件A包含的样本点有:(生,化),共1个
由古典概型概率计算公式得
所以学生甲选化学和生物的概率是.
典例讲解
二、古典概型的概率求解
解
(2)记“学生乙不选政治但选生物”为事件B.
学生乙在“1”中任选1科,在“2”中任选2科的样本点有:(物,生,化),(物,生,政),(物,生,地),(物,化,政), (物,化,地),(物,政,地),(史,生,化),(史,生,政),(史,生,地),(史,化,政),(史,化,地),(史,政,地),共12个.事件B包含的样本点有:(物,生,化),(物,生,地),(史,生,化),(史,生,地),共4个.
由古典概型概率计算公式得所以学生乙不选政治但选生物的概率是
典例讲解
知识归纳
1. 对任意两个事件A与B,如果它们满足,那么它们就是相互独立事件,是相互独立事件就可以利用这个公式进行概率计算,也就是说两个相互独立事件同时发生的概率等于每个事件发生的概率的乘积.
2. 还需注意独立性的一个重要性质,即:如果事件 与 相互独立,那么也都相互独立.
主要考查角度:
相互独立事件的概率计算.
三、事件的相互独立性
例6、甲、乙、丙三人进行投篮练习,他们投中的概率分别是,且三人投中与否相互之间没有影响,则他们三人中至少有一人投中的概率为 ( )
甲、乙、丙三人进行投篮练习,他们投中的概率分别是
且三人投中与否相互之间没有影响,
他们三人中至少有一人投中的概率为
解析
三、事件的相互独立性
典例讲解
例7、一道试题,A,B,C三人可解出的概率分别为,则三人独立解答,只有一人解出试题的概率为( )
根据题意,只有一人解出试题的事件包含“解出而其余两人没有解出,解出而其余两人没有解出,解出而其余两人没有解出”三个互斥事件,而三人解出试题是相互独立的,则(只有一人解出试题)
解析
三、事件的相互独立性
典例讲解
知识归纳
1. 随机事件在一次试验中是否发生具有不确定性,但是,在相同条件下的大量重复试验中,频率偏离概率的幅度会缩小,即事件发生的频率
会逐渐稳定于事件发生的概率,称频率的这个性质为频率的稳定性.用频率估计概率
2. 用整数随机模拟试验估计概率时,首先要确定随机数的范围和用哪些数代表不同的试验结果.当试验的基本事件等可能时,基本事件总数即产生随机数的范围,每个随机数代表一个样本点.
主要考查角度:(1)利用频率估计概率;(2)随机模拟问题.
四、频率与概率
典例讲解
例8、已知种植某种树苗的成活率为0.9,现采用随机模拟的方法估计种植这种树苗5棵恰好成活4棵的概率:先利用计算器产生0到9之间的取整数值的随机数,用0代表不成活,用1~9的数字代表成活,再以5个随机数为1组,代表种植5棵树苗的结果.通过模拟试验产生了30组随机数:
据此估计种植这种树苗5棵恰好成活4棵的概率是( )
四、频率与概率
这就相当于做了30次试验,在这些数组中,如果恰有一个0,则表示恰有4棵成活,共有9组这样的数,于是我们得到种植5棵这种树苗恰有4棵成活的概率约为
解析
四、频率与概率
典例讲解
例9、某险种的基本保费为(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
四、频率与概率
典例讲解
(1)记为事件“一续保人本年度的保费不高于基本保费”,求的估计值;
(2)记 为事件“一续保人本年度的保费高于基本保费但不高于基本保费的”,求的估计值;
(3)求续保人本年度平均保费的估计值.
将频数转化为频率,利用频率估计概率.
解析
四、频率与概率
典例讲解
解
(1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为,故的估计值为
(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为,故的估计值为.
(3)由所给数据得下表:
调查的200名续保人的平均保费为
四、频率与概率
因此,续保人本年度平均保费的估计值为1.1925
典例讲解
例10、为备战奥运会,某射击运动员在相同条件下进行射击训练,结果如下表:
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
四、频率与概率
典例讲解
利用频率估计概率.
解析
解
(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270.
(3)由概率的意义可知概率是个常数,不因试验次数的变化而变化,故第10次击中靶心的概率仍大约是0.9,所以不一定击中靶心.
四、频率与概率
典例讲解
人教A版同步教材名师课件
概率
建构知识网络
洞悉高考
专题分布 考点频次 考试分值 命题热点
了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别 ★★ 5年18考 学考赋分 5~10分 【内容特点】利用频率估计概率;求古典概型的概率,求几何概型的概率,古典概型与统计的综合问题
【题型形式】以选择题、填空题、解答题.
如2017·江苏·T3,2018·全国I·T19,全国卷Ⅱ·理·T10,2018·北京·T17,2018·江苏·T7,2018·天津·T15.
了解两个互斥事件的概率加法公式 ★★ 5年18考
了解事件的相互独立性 ★★ 5年18考
理解古典概型及其概率计算公式 ★★ 5年24考 高考赋分 5~12分
会用列举法计算一些随机事件所含的样本,点个数及事件发生的概率 ★★ 5年24考
了解随机数的意义,能运用随机模拟的方法估计概率 ★★★ 5年36考
知识归纳
随机事件主要包括三个方面的内容:有限样本空间、事件的关系和运算、概率的基本性质.
1. 对于有限样本空间,要紧紧抓住随机试验的三个特点和样本空间的概念,正确列出样本空间,为后面解决古典概型打下良好的基础.
2. 关于事件的关系和运算,类比集合的相关运算法则,重点区分互斥事件和对立事件.
一、随机事件
知识归纳
3. 关于概率的六条基本性质,其中互斥事件的概率之和与对立事件的概率之差仍是我们求概率运算的主体.对于性质6;设A,B是一个随机试验中的两个事件,有
要引起高度的注意,注意其使用的条件.
4. 应用互斥事件的概率的加法公式解题时,一定要注意首先各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于复杂事件的概率,可以转化为求其对立事件的概率.主要考查角度:(1)事件的样本空间;(2)事件关系的判定; (3)互斥事件与对立事件的概率.
一、随机事件
例1、2021年某省新高考将实行“3+1+2”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件A:“他选择政治和地理”,事件B:“他选择化学和地理”,则事件A与事件B ( )
A.是互斥事件,但不是对立事件 B.是对立事件,但不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件,也不是对立事件
事件A:“他选择政治和地理”,事件B:“他选择化学和地理”,则事件A与事件B不能同时发生,但能同时不发生,故事件A和事件B是互斥事件,但不是对立事件.
解析
一、随机事件
典例讲解
例2、某商场有奖销售中,每购物满100元可抽取1张奖券,多购多得,每1000张奖券为一个开奖单位.设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为求:
;
抽取1张奖券中奖的概率;
抽取1张奖券不中特等奖或一等奖的概率
对于(1)直接求解;对于(2)(3)应明确要求事件中包含哪些事件.
解析
一、随机事件
典例讲解
一、随机事件
解
由题意知,事件为互斥事件.
(1)每1000张奖券中设特等奖1个,一等奖10个,二等奖50个,
(2) 设“抽取1张奖券中奖”为事件D,则
(3) 设“抽取1张奖券不中特等奖或一等奖”为事件E
典例讲解
知识归纳
1. 古典概型是一种最基本的概型,也是学习其他概型的基础,解决这类问题要紧紧抓住古典概型的两个基本特征,即有限性和等可能性.
2. 对古典概型概率的计算,关键是分清样本空间包含个样本点,事件A包含其中的个样本点,有时需要用列举法把样本空间一一列举出来,再利用公式求出事件的概率,这是一个形象、直观的好方法,但列举时必须按某一顺序做到不重复、不遗漏.
主要考查角度:古典概型的概率求解.
二、古典概型的概率求解
例3、某购物中心举行抽奖活动,顾客从装有编号分别为 四个球的抽奖箱中,每次取出1个球,记下编号后放回,连续取两次(假设取到任何一个小球的可能性相同).若取出的两个小球号码相加之和等于5,则中一等奖;若取出的两个小球号码相加之和等于4,则中二等奖;若取出的两个小球号码相加之和等于3,则中三等奖;其他情况不中奖.
(1)求顾客中三等奖的概率;(2)求顾客未中奖的概率.
根据题目条件,列出样本空间,然后按照古典概型和概率的性质进行求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)设事件A为“顾客中三等奖”,所有样本点包括
所以顾客中三等奖的概率为
典例讲解
二、古典概型的概率求解
解
(2)设事件B为“顾客未中奖”,
“两个小球号码相加之和等于5”这一事件包括样本点(2,3),(3,2),共2个.
“两个小球号码相加之和等于4”这一事件包括样本点
所以
所以顾客未中奖的概率为
典例讲解
例4、已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(i i )设为事件“抽取的2名同学来自同一年级”,求事件发生的概率.
根据分层抽样的方法确定从甲、乙、丙三个年级的学生志愿者中分别抽取的人数,然后按照要求列出样本空间,进行概率求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人、2人、2人.
(2)(i)从抽出的7名同学中随机抽取2名同学的所有可能结果为
,共21种.
(ii)由(1),不妨设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为 共5种.所以事件 发生的概率
典例讲解
例5、2021年福建省高考实行“3+1+2” 模式.“3+1+2”模式是指:“3”为全国统考科目语文、数学、外语,所有学生必考;“1”为首选科目,考生须在高中学业水平考试的物理、历史科目中选择1科;“2”为再选科目,考生可在化学、生物、政治、地理4个科目中选择2科,共计6个考试科目.
(1)若学生甲在“1”中选物理,在“2”中任选2科,求学生甲选化学和生物的概率;(2)若学生乙在“1”中任选1科,在“2”中任选2科,求学生乙不选政治但选生物的概率.
对于(1)(2)两问,由于各自要求的条件不一样,需要各自列出样本空间,然后找出发生事件,从而按照古典概型的概率公式求解.
解析
二、古典概型的概率求解
典例讲解
二、古典概型的概率求解
解
(1)记“学生甲选化学和生物”为事件A
学生甲在“1”中选物理,在“2”中任选2科的样本点有:(生,化),(生,政),(生,地),(化,政),(化,地),(政,地),共6个.
事件A包含的样本点有:(生,化),共1个
由古典概型概率计算公式得
所以学生甲选化学和生物的概率是.
典例讲解
二、古典概型的概率求解
解
(2)记“学生乙不选政治但选生物”为事件B.
学生乙在“1”中任选1科,在“2”中任选2科的样本点有:(物,生,化),(物,生,政),(物,生,地),(物,化,政), (物,化,地),(物,政,地),(史,生,化),(史,生,政),(史,生,地),(史,化,政),(史,化,地),(史,政,地),共12个.事件B包含的样本点有:(物,生,化),(物,生,地),(史,生,化),(史,生,地),共4个.
由古典概型概率计算公式得所以学生乙不选政治但选生物的概率是
典例讲解
知识归纳
1. 对任意两个事件A与B,如果它们满足,那么它们就是相互独立事件,是相互独立事件就可以利用这个公式进行概率计算,也就是说两个相互独立事件同时发生的概率等于每个事件发生的概率的乘积.
2. 还需注意独立性的一个重要性质,即:如果事件 与 相互独立,那么也都相互独立.
主要考查角度:
相互独立事件的概率计算.
三、事件的相互独立性
例6、甲、乙、丙三人进行投篮练习,他们投中的概率分别是,且三人投中与否相互之间没有影响,则他们三人中至少有一人投中的概率为 ( )
甲、乙、丙三人进行投篮练习,他们投中的概率分别是
且三人投中与否相互之间没有影响,
他们三人中至少有一人投中的概率为
解析
三、事件的相互独立性
典例讲解
例7、一道试题,A,B,C三人可解出的概率分别为,则三人独立解答,只有一人解出试题的概率为( )
根据题意,只有一人解出试题的事件包含“解出而其余两人没有解出,解出而其余两人没有解出,解出而其余两人没有解出”三个互斥事件,而三人解出试题是相互独立的,则(只有一人解出试题)
解析
三、事件的相互独立性
典例讲解
知识归纳
1. 随机事件在一次试验中是否发生具有不确定性,但是,在相同条件下的大量重复试验中,频率偏离概率的幅度会缩小,即事件发生的频率
会逐渐稳定于事件发生的概率,称频率的这个性质为频率的稳定性.用频率估计概率
2. 用整数随机模拟试验估计概率时,首先要确定随机数的范围和用哪些数代表不同的试验结果.当试验的基本事件等可能时,基本事件总数即产生随机数的范围,每个随机数代表一个样本点.
主要考查角度:(1)利用频率估计概率;(2)随机模拟问题.
四、频率与概率
典例讲解
例8、已知种植某种树苗的成活率为0.9,现采用随机模拟的方法估计种植这种树苗5棵恰好成活4棵的概率:先利用计算器产生0到9之间的取整数值的随机数,用0代表不成活,用1~9的数字代表成活,再以5个随机数为1组,代表种植5棵树苗的结果.通过模拟试验产生了30组随机数:
据此估计种植这种树苗5棵恰好成活4棵的概率是( )
四、频率与概率
这就相当于做了30次试验,在这些数组中,如果恰有一个0,则表示恰有4棵成活,共有9组这样的数,于是我们得到种植5棵这种树苗恰有4棵成活的概率约为
解析
四、频率与概率
典例讲解
例9、某险种的基本保费为(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
四、频率与概率
典例讲解
(1)记为事件“一续保人本年度的保费不高于基本保费”,求的估计值;
(2)记 为事件“一续保人本年度的保费高于基本保费但不高于基本保费的”,求的估计值;
(3)求续保人本年度平均保费的估计值.
将频数转化为频率,利用频率估计概率.
解析
四、频率与概率
典例讲解
解
(1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为,故的估计值为
(2)事件B发生当且仅当一年内出险次数大于1且小于4.由所给数据知,一年内出险次数大于1且小于4的频率为,故的估计值为.
(3)由所给数据得下表:
调查的200名续保人的平均保费为
四、频率与概率
因此,续保人本年度平均保费的估计值为1.1925
典例讲解
例10、为备战奥运会,某射击运动员在相同条件下进行射击训练,结果如下表:
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?
四、频率与概率
典例讲解
利用频率估计概率.
解析
解
(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270.
(3)由概率的意义可知概率是个常数,不因试验次数的变化而变化,故第10次击中靶心的概率仍大约是0.9,所以不一定击中靶心.
四、频率与概率
典例讲解
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
