人教A版(2019)高中数学必修第二册 第十章_概率测试(解析版)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册 第十章_概率测试(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 452.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 09:05:44 | ||
图片预览




文档简介
第十章 概率测试
一、单选题(每题5分,共60分)
1.有编号为,,的三个盒子和编号分别为,,的三个小球,每个盒子放入一个小球,则小球的编号与盒子编号全不相同的概率为( )
A. B. C. D.
2.把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
3.从这五个数字中随机选择两个不同的数字,则它们之和为偶数的概率为( )
A. B. C. D.
4.设事件,,已知, ,,则,之间的关系一定为
A.两个任意事件 B.互斥事件 C.非互斥事件 D.对立事件
5.以下现象是随机现象的是( )
A.标准大气压下,水加热到100℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为
C.走到十字路口,遇到红灯
D.三角形内角和为180°
6.某种彩票中奖的概率为,这是指( )
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
7.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
A.4件都是正品 B.至少有一件次品
C.4件都是次品 D.至少有一件正品
8.一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件是
A.随机事件 B.必然事件 C.不可能事件 D.不能确定
9.掷一枚骰子的试验中,出现各点的概率均为,事件表示“出现小于5的偶数点”,事件表示“出现小于5的点数”,则一次试验中,事件(表示事件的对立事件)发生的概率为
A. B. C. D.
10.甲:、是互斥事件;乙:、是对立事件,那么( )
A.甲是乙的充要条件B.甲是乙的充分但不必要条件
C.甲是乙的必要但不充分条件D.甲既不是乙的充分条件,也不是乙的必要条件
11.若某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,则仅用非现金支付的概率为( )
A.0.2 B.0.4 C.0.5 D.0.8
12.青岛二中戏剧节中,6个MT除人文MT有两个节目参加决赛外,其他MT各有一个节目参加决赛,一共7个节目,在决赛中,要从这7支队伍中随机抽取两支队伍比赛,则人文MT两支队伍不同时被抽到的概率为( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个,取得两个红玻璃球的概率为,取得两个绿玻璃球的概率为,则取得两个同颜色的玻璃球的概率为________;至少取得一个红玻璃球的概率为________.
14.有以下说法:
①一年按365天计算,两名学生的生日相同的概率是;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
15.①某人射击一次,中靶;②从一副牌中抽到红桃A;③种下一粒种子发芽;④掷一枚骰子,出现6点.其中是随机现象的是_____.
16.从1,2,3,4,5这5个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;
②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;
④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是________.
三、解答题(17题10分,其余12分,共70分)
17.某单位利用“学习强国”平台,开展网上学习,实行积分制.为了了解积分情况,随机调查了名员工,得到这些员工学习得分频数分布表:
得分
人数
(Ⅰ)求这些员工学习得分的平均数(同一组中的数据用该组区间的中点值为代表);
(Ⅱ)用分层抽样的方法从得分在和的员工中选取人.从选取的人中,再任选取人,求得分在和中各有人的概率.
18.某超市随机选取位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
√ × √ √
× √ × √
√ √ √ ×
√ × √ ×
85 √ × × ×
× √ × ×
(1)估计顾客同时购买乙和丙的概率;
(2)估计顾客在甲、乙、丙、丁中同时购买中商品的概率;
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
19.某班选派5人,参加学校举行的数学竞赛,获奖的人数及其概率如下:
获奖人数 0 1 2 3 4 5
概率 0.1 0.16 x y 0.2 z
(1)若获奖人数不超过2人的概率为0.56,求x的值;
(2)若获奖人数最多4人的概率为0.96,最少3人的概率为0.44,求y,z的值.
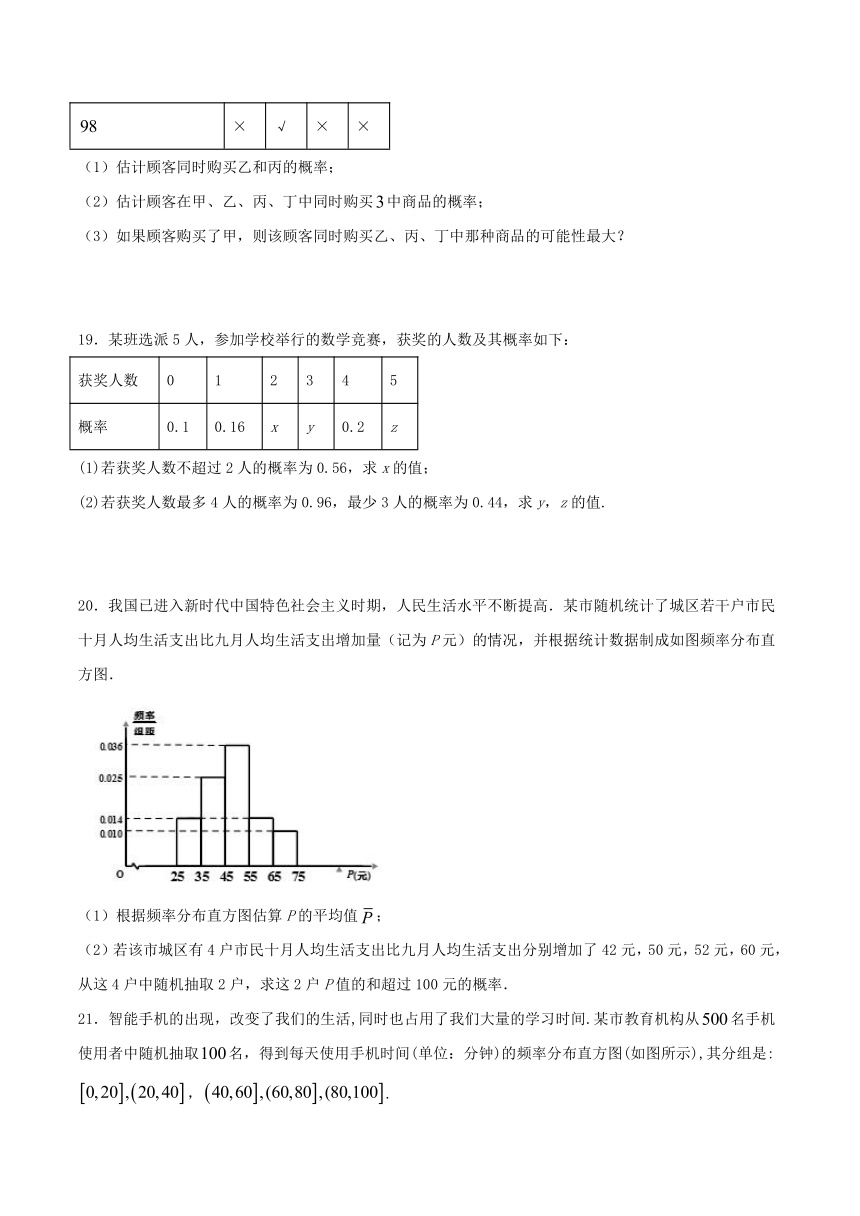
20.我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
(1)根据频率分布直方图估算P的平均值;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
21.智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从名手机使用者中随机抽取名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: ,.
(1)根据频率分布直方图,估计这名手机使用者中使用时间的中位数是多少分钟 (精确到整数)
(2)估计手机使用者平均每天使用手机多少分钟 (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的名手机使用者中在和中按比例分别抽取人和人组成研究小组,然后再从研究小组中选出名组长.求这名组长分别选自和的概率是多少?
22.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 第一类 第二类 第三类 第四类 第五类 第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
第十章 概率测试答案
一、单选题(每题5分,共60分)
1.有编号为,,的三个盒子和编号分别为,,的三个小球,每个盒子放入一个小球,则小球的编号与盒子编号全不相同的概率为( )
A. B. C. D.
【来源】2020届陕西省咸阳市高三上学期期末考试数学(文)试题
【答案】D以表示编号为、、的盒子分别放编号为、、的小球,则所有的基本事件有:、、、、、,共种,
其中,事件“小球的编号与盒子编号全不相同”所包含的基本事件有:、,共个,因此,小球的编号与盒子编号全不相同的概率为.故选:D.
2.把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
【来源】2019年3月21日《每日一题》必修3概率的基本性质(1)
【答案】B
【解析】因为事件“甲分得红牌”与事件“乙分得红牌”不可能同时发生,所以它们是互斥事件,因为事件“甲分得红牌”与事件“乙分得红牌”不包含所有的可能事件,所以它们不是对立事件,所以它们是互斥但不对立事件,故选B。
3.从这五个数字中随机选择两个不同的数字,则它们之和为偶数的概率为()
A. B. C. D.
【来源】四川省百校2019年高三模拟冲刺卷理科数学试题
【答案】B
【解析】从1、2、3、4、5、这五个数字中,随机抽取两个不同的数字,
基本事件总数n,
这两个数字的和为偶数包含的基本事件个数m4,
∴这两个数字的和为偶数的概率为p.
故选:B.
4.设事件,,已知, ,,则,之间的关系一定为
A.两个任意事件 B.互斥事件 C.非互斥事件 D.对立事件
【来源】专题11.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】B
【解析】,,
又
.为互相斥事件
故选:.
5.以下现象是随机现象的是()
A.标准大气压下,水加热到100℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为
C.走到十字路口,遇到红灯
D.三角形内角和为180°
【来源】辽宁省葫芦岛市2018-2019学年高一下学期期末考试数学试题
【答案】C
【解析】A. 标准大气压下,水加热到100℃,必会沸腾,是必然事件;
B. 长和宽分别为a,b的矩形,其面积为,是必然事件;
C. 走到十字路口,遇到红灯,是随机事件;
D. 三角形内角和为180°,是必然事件.
故选C
6.某种彩票中奖的概率为,这是指( )
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
【来源】江苏省无锡市普通高中2018-2019学年高一下学期期末数学试题
【答案】D
【解析】彩票中奖的概率为,只是指中奖的可能性为,
不是买10000张彩票一定能中奖,
概率是指试验次数越来越大时,频率越接近概率。所以选D.
7.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
A.4件都是正品 B.至少有一件次品
C.4件都是次品 D.至少有一件正品
【来源】黑龙江省双鸭山市第一中学2016-2017学年高二4月月考数学(文)试题
【答案】D
【解析】抽取4件中至多3件次品,即至少有一件正品,选D.
8.一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件是
A.随机事件 B.必然事件 C.不可能事件 D.不能确定
【来源】黑龙江省哈尔滨六中2018-2019学年高二(上)期中考试数学(文)试题
【答案】A
【解析】一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件可能发生也可能不发生,所以是随机事件,故选A.
9.掷一枚骰子的试验中,出现各点的概率均为,事件表示“出现小于5的偶数点”,事件表示“出现小于5的点数”,则一次试验中,事件(表示事件的对立事件)发生的概率为
A. B. C. D.
【来源】专题10.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】C
【解析】事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:.
10.甲:、是互斥事件;乙:、是对立事件,那么( )
A.甲是乙的充要条件B.甲是乙的充分但不必要条件
C.甲是乙的必要但不充分条件D.甲既不是乙的充分条件,也不是乙的必要条件
【来源】辽宁省部分重点中学协作体2018届高三模拟考试文科数学试题
【答案】C
【解析】当、是互斥事件时,、不一定是对立事件,所以甲是乙的非充分条件.
当、是对立事件时,、一定是互斥事件,所以甲是乙的必要条件.
所以甲是乙的必要非充分条件.
故选C.
11.若某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,则仅用非现金支付的概率为( )
A.0.2 B.0.4 C.0.5 D.0.8
【来源】北京市石景山区2019-2020学年高一上学期期末数学试题
【答案】C
【解析】某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,∴不用现金支付的概率为:p=1-0.15-0.35=0.5.故选:C
12.青岛二中戏剧节中,6个MT除人文MT有两个节目参加决赛外,其他MT各有一个节目参加决赛,一共7个节目,在决赛中,要从这7支队伍中随机抽取两支队伍比赛,则人文MT两支队伍不同时被抽到的概率为( )
A. B. C. D.
【来源】山东省青岛市青岛第二中学2018-2019学年高二上学期期末数学试题
【答案】B
【解析】从这7支队伍中随机抽取两支队伍比赛,总共有种可能,
人文两支队伍同时被抽到的共有2种情况,
所以人文两支队伍不同时被抽到的概率为,
故选:.
二、填空题(每题5分,共20分)
13.在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个,取得两个红玻璃球的概率为,取得两个绿玻璃球的概率为,则取得两个同颜色的玻璃球的概率为________;至少取得一个红玻璃球的概率为________.
【来源】专题10.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】
【解析】取得两个同颜色的玻璃球包括两个红玻璃球或两个绿玻璃球故取得两个同颜色的玻璃球的概率;
“至少取得一个红玻璃球”的对立事件是“取得两个绿玻璃球”
故至少取得一个红玻璃球的概率
故答案为:;
14.有以下说法:
①一年按365天计算,两名学生的生日相同的概率是;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
【来源】人教B版高中数学必修三同步测试:模块复习课3 概率
【答案】①③
【解析】根据“概率的意义”求解,买彩票中奖的概率0.001,并不意味着买1 000张彩票一定能中奖,只有当买彩票的数量非常大时,我们可以看成大量买彩票的重复试验,中奖的次数为;
昨天气象局的天气预报降水概率是90%,是指可能性非常大,并不一定会下雨.
说法②④是错误的,而利用概率知识可知①③是正确的.
故答案为①③.
15.①某人射击一次,中靶;②从一副牌中抽到红桃A;③种下一粒种子发芽;④掷一枚骰子,出现6点.其中是随机现象的是_____.
【来源】人教B版高中数学必修三同步测试:3.1.1-3.1.2 随机现象 事件与基本事件空间
【答案】①②③④
【解析】根据随机现象的定义知①②③④是随机现象,故填①②③④.
16.从1,2,3,4,5这5个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;
②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;
④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是________.
【来源】陕西省宝鸡市金台区2019-2020学年高三教学质量检测数学文试题
【答案】③
【解析】①恰有一个是偶数和恰有一个是奇数不是互斥事件,也不是对立事件;
②至少有一个是奇数和两个都是奇数不是互斥事件,也不是对立事件;
③至少有一个是奇数和两个都是偶数是互斥事件,也是对立事件;
④至少有一个是奇数和至少有一个是偶数不是互斥事件,也不是对立事件;
故答案为:③
三、解答题(17题10分,其余12分,共70分)
17.某单位利用“学习强国”平台,开展网上学习,实行积分制.为了了解积分情况,随机调查了名员工,得到这些员工学习得分频数分布表:
得分
人数
(Ⅰ)求这些员工学习得分的平均数(同一组中的数据用该组区间的中点值为代表);
(Ⅱ)用分层抽样的方法从得分在和的员工中选取人.从选取的人中,再任选取人,求得分在和中各有人的概率.
【来源】2020届陕西省咸阳市高三上学期期末考试数学(文)试题
【答案】(Ⅰ);(Ⅱ).
【解析】(Ⅰ)记这名员工学习得分的平均数为,
则;
(Ⅱ)用分层抽样可知从中选人,记这人分别为、,
从中选人,记这人分别为、、.
从、、、、中再任取人的情况有:
、、、、、、、、、,共种.
其中得分在和中各有人的情况有:
、、、、、,共种.
记事件为“得分在和中各有人”,则.
18.某超市随机选取位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
√ × √ √
× √ × √
√ √ √ ×
√ × √ ×
85 √ × × ×
× √ × ×
(1)估计顾客同时购买乙和丙的概率;
(2)估计顾客在甲、乙、丙、丁中同时购买中商品的概率;
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
【来源】北京十二中2016-2017学年下学期高二期中试卷 数学(文科)
【答案】(1)0.2;(2)0.3;(3)丙
【解析】 (1)从统计表可以看出,在这1 000位顾客中有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为=0.2.
(2)从统计表可以看出,在这1 000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品.
所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为=0.3.
(3)与(1)同理,可得:顾客同时购买甲和乙的概率可以估计为=0.2,顾客同时购买甲和丙的概率可以估计为=0.6,顾客同时购买甲和丁的概率可以估计为=0.1.所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大.
19.某班选派5人,参加学校举行的数学竞赛,获奖的人数及其概率如下:
获奖人数 0 1 2 3 4 5
概率 0.1 0.16 x y 0.2 z
(1)若获奖人数不超过2人的概率为0.56,求x的值;
(2)若获奖人数最多4人的概率为0.96,最少3人的概率为0.44,求y,z的值.
【来源】专题10.7第十章 统计与统计案例、概率(单元测试)(测)-《2020年高考一轮复习讲练测》
【答案】(1) 0.3;(2) y=0.2, z=0.04.
【解析】记事件“在竞赛中,有k人获奖”为Ak(k∈N,k≤5),则事件Ak彼此互斥.
(1)∵获奖人数不超过2人的概率为0.56,
∴P(A0)+P(A1)+P(A2)=0.1+0.16+x=0.56.
解得x=0.3.
(2)由获奖人数最多4人的概率为0.96,得P(A5)=1-0.96=0.04,即z=0.04.
由获奖人数最少3人的概率为0.44,得P(A3)+P(A4)+P(A5)=0.44,即y+0.2+0.04=0.44.
解得y=0.2.
20.我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
(1)根据频率分布直方图估算P的平均值;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
【来源】2020届四川省达州市普通高中高三第一次诊断性测试数学(文)试题
【答案】(1)48 (2)
【解析】(1)根据频率分布直方图估算的平均值:
.
(2)该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,
从这4户中随机抽取2户,
基本事件总数,
这2户值的和超过100元包含的基本事件有,,,,共4个,
这2户值的和超过100元的概率.
21.智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从名手机使用者中随机抽取名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: ,.
(1)根据频率分布直方图,估计这名手机使用者中使用时间的中位数是多少分钟 (精确到整数)
(2)估计手机使用者平均每天使用手机多少分钟 (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的名手机使用者中在和中按比例分别抽取人和人组成研究小组,然后再从研究小组中选出名组长.求这名组长分别选自和的概率是多少?
【来源】辽宁省锦州市2018-2019学年高一下学期期末数学试题
【答案】(1) 分钟. (2)58分钟;(3)
【解析】(1)设中位数为,则
解得:(分钟)
这名手机使用者中使用时间的中位数是分钟
(2)平均每天使用手机时间为:(分钟)
即手机使用者平均每天使用手机时间为分钟
(3)设在内抽取的两人分别为,在内抽取的三人分别为,
则从五人中选出两人共有以下种情况:
两名组长分别选自和的共有以下种情况:
所求概率
22.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 第一类 第二类 第三类 第四类 第五类 第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
【来源】2018年全国普通高等学校招生统一考试文科数学(北京卷)
【答案】(Ⅰ);(Ⅱ);(Ⅲ)增加第五类电影的好评率,减少第二类电影的好评率.
【解析】(Ⅰ)由题意知,样本中电影的总部数是,
第四类电影中获得好评的电影部数是,
故所求概率为;
(Ⅱ)设“随机选取部电影,这部电影没有获得好评”为事件B.
没有获得好评的电影共有部,
由古典概型概率公式得;
(Ⅲ)增加第五类电影的好评率, 减少第二类电影的好评率.
一、单选题(每题5分,共60分)
1.有编号为,,的三个盒子和编号分别为,,的三个小球,每个盒子放入一个小球,则小球的编号与盒子编号全不相同的概率为( )
A. B. C. D.
2.把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
3.从这五个数字中随机选择两个不同的数字,则它们之和为偶数的概率为( )
A. B. C. D.
4.设事件,,已知, ,,则,之间的关系一定为
A.两个任意事件 B.互斥事件 C.非互斥事件 D.对立事件
5.以下现象是随机现象的是( )
A.标准大气压下,水加热到100℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为
C.走到十字路口,遇到红灯
D.三角形内角和为180°
6.某种彩票中奖的概率为,这是指( )
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
7.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
A.4件都是正品 B.至少有一件次品
C.4件都是次品 D.至少有一件正品
8.一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件是
A.随机事件 B.必然事件 C.不可能事件 D.不能确定
9.掷一枚骰子的试验中,出现各点的概率均为,事件表示“出现小于5的偶数点”,事件表示“出现小于5的点数”,则一次试验中,事件(表示事件的对立事件)发生的概率为
A. B. C. D.
10.甲:、是互斥事件;乙:、是对立事件,那么( )
A.甲是乙的充要条件B.甲是乙的充分但不必要条件
C.甲是乙的必要但不充分条件D.甲既不是乙的充分条件,也不是乙的必要条件
11.若某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,则仅用非现金支付的概率为( )
A.0.2 B.0.4 C.0.5 D.0.8
12.青岛二中戏剧节中,6个MT除人文MT有两个节目参加决赛外,其他MT各有一个节目参加决赛,一共7个节目,在决赛中,要从这7支队伍中随机抽取两支队伍比赛,则人文MT两支队伍不同时被抽到的概率为( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个,取得两个红玻璃球的概率为,取得两个绿玻璃球的概率为,则取得两个同颜色的玻璃球的概率为________;至少取得一个红玻璃球的概率为________.
14.有以下说法:
①一年按365天计算,两名学生的生日相同的概率是;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
15.①某人射击一次,中靶;②从一副牌中抽到红桃A;③种下一粒种子发芽;④掷一枚骰子,出现6点.其中是随机现象的是_____.
16.从1,2,3,4,5这5个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;
②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;
④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是________.
三、解答题(17题10分,其余12分,共70分)
17.某单位利用“学习强国”平台,开展网上学习,实行积分制.为了了解积分情况,随机调查了名员工,得到这些员工学习得分频数分布表:
得分
人数
(Ⅰ)求这些员工学习得分的平均数(同一组中的数据用该组区间的中点值为代表);
(Ⅱ)用分层抽样的方法从得分在和的员工中选取人.从选取的人中,再任选取人,求得分在和中各有人的概率.
18.某超市随机选取位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
√ × √ √
× √ × √
√ √ √ ×
√ × √ ×
85 √ × × ×
× √ × ×
(1)估计顾客同时购买乙和丙的概率;
(2)估计顾客在甲、乙、丙、丁中同时购买中商品的概率;
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
19.某班选派5人,参加学校举行的数学竞赛,获奖的人数及其概率如下:
获奖人数 0 1 2 3 4 5
概率 0.1 0.16 x y 0.2 z
(1)若获奖人数不超过2人的概率为0.56,求x的值;
(2)若获奖人数最多4人的概率为0.96,最少3人的概率为0.44,求y,z的值.
20.我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
(1)根据频率分布直方图估算P的平均值;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
21.智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从名手机使用者中随机抽取名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: ,.
(1)根据频率分布直方图,估计这名手机使用者中使用时间的中位数是多少分钟 (精确到整数)
(2)估计手机使用者平均每天使用手机多少分钟 (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的名手机使用者中在和中按比例分别抽取人和人组成研究小组,然后再从研究小组中选出名组长.求这名组长分别选自和的概率是多少?
22.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 第一类 第二类 第三类 第四类 第五类 第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
第十章 概率测试答案
一、单选题(每题5分,共60分)
1.有编号为,,的三个盒子和编号分别为,,的三个小球,每个盒子放入一个小球,则小球的编号与盒子编号全不相同的概率为( )
A. B. C. D.
【来源】2020届陕西省咸阳市高三上学期期末考试数学(文)试题
【答案】D以表示编号为、、的盒子分别放编号为、、的小球,则所有的基本事件有:、、、、、,共种,
其中,事件“小球的编号与盒子编号全不相同”所包含的基本事件有:、,共个,因此,小球的编号与盒子编号全不相同的概率为.故选:D.
2.把红、黄、蓝、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件 B.互斥但不对立事件
C.不可能事件 D.以上都不对
【来源】2019年3月21日《每日一题》必修3概率的基本性质(1)
【答案】B
【解析】因为事件“甲分得红牌”与事件“乙分得红牌”不可能同时发生,所以它们是互斥事件,因为事件“甲分得红牌”与事件“乙分得红牌”不包含所有的可能事件,所以它们不是对立事件,所以它们是互斥但不对立事件,故选B。
3.从这五个数字中随机选择两个不同的数字,则它们之和为偶数的概率为()
A. B. C. D.
【来源】四川省百校2019年高三模拟冲刺卷理科数学试题
【答案】B
【解析】从1、2、3、4、5、这五个数字中,随机抽取两个不同的数字,
基本事件总数n,
这两个数字的和为偶数包含的基本事件个数m4,
∴这两个数字的和为偶数的概率为p.
故选:B.
4.设事件,,已知, ,,则,之间的关系一定为
A.两个任意事件 B.互斥事件 C.非互斥事件 D.对立事件
【来源】专题11.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】B
【解析】,,
又
.为互相斥事件
故选:.
5.以下现象是随机现象的是()
A.标准大气压下,水加热到100℃,必会沸腾
B.长和宽分别为a,b的矩形,其面积为
C.走到十字路口,遇到红灯
D.三角形内角和为180°
【来源】辽宁省葫芦岛市2018-2019学年高一下学期期末考试数学试题
【答案】C
【解析】A. 标准大气压下,水加热到100℃,必会沸腾,是必然事件;
B. 长和宽分别为a,b的矩形,其面积为,是必然事件;
C. 走到十字路口,遇到红灯,是随机事件;
D. 三角形内角和为180°,是必然事件.
故选C
6.某种彩票中奖的概率为,这是指( )
A.买10000张彩票一定能中奖
B.买10000张彩票只能中奖1次
C.若买9999张彩票未中奖,则第10000张必中奖
D.买一张彩票中奖的可能性是
【来源】江苏省无锡市普通高中2018-2019学年高一下学期期末数学试题
【答案】D
【解析】彩票中奖的概率为,只是指中奖的可能性为,
不是买10000张彩票一定能中奖,
概率是指试验次数越来越大时,频率越接近概率。所以选D.
7.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
A.4件都是正品 B.至少有一件次品
C.4件都是次品 D.至少有一件正品
【来源】黑龙江省双鸭山市第一中学2016-2017学年高二4月月考数学(文)试题
【答案】D
【解析】抽取4件中至多3件次品,即至少有一件正品,选D.
8.一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件是
A.随机事件 B.必然事件 C.不可能事件 D.不能确定
【来源】黑龙江省哈尔滨六中2018-2019学年高二(上)期中考试数学(文)试题
【答案】A
【解析】一个口袋中装有大小和形状都相同的一个白球和一个黑球,那么“从中任意摸一个球得到白球”,这个事件可能发生也可能不发生,所以是随机事件,故选A.
9.掷一枚骰子的试验中,出现各点的概率均为,事件表示“出现小于5的偶数点”,事件表示“出现小于5的点数”,则一次试验中,事件(表示事件的对立事件)发生的概率为
A. B. C. D.
【来源】专题10.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】C
【解析】事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:.
10.甲:、是互斥事件;乙:、是对立事件,那么( )
A.甲是乙的充要条件B.甲是乙的充分但不必要条件
C.甲是乙的必要但不充分条件D.甲既不是乙的充分条件,也不是乙的必要条件
【来源】辽宁省部分重点中学协作体2018届高三模拟考试文科数学试题
【答案】C
【解析】当、是互斥事件时,、不一定是对立事件,所以甲是乙的非充分条件.
当、是对立事件时,、一定是互斥事件,所以甲是乙的必要条件.
所以甲是乙的必要非充分条件.
故选C.
11.若某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,则仅用非现金支付的概率为( )
A.0.2 B.0.4 C.0.5 D.0.8
【来源】北京市石景山区2019-2020学年高一上学期期末数学试题
【答案】C
【解析】某群体中的成员只用现金支付的概率为0.15,既用现金支付也用非现金支付的概率为0.35,∴不用现金支付的概率为:p=1-0.15-0.35=0.5.故选:C
12.青岛二中戏剧节中,6个MT除人文MT有两个节目参加决赛外,其他MT各有一个节目参加决赛,一共7个节目,在决赛中,要从这7支队伍中随机抽取两支队伍比赛,则人文MT两支队伍不同时被抽到的概率为( )
A. B. C. D.
【来源】山东省青岛市青岛第二中学2018-2019学年高二上学期期末数学试题
【答案】B
【解析】从这7支队伍中随机抽取两支队伍比赛,总共有种可能,
人文两支队伍同时被抽到的共有2种情况,
所以人文两支队伍不同时被抽到的概率为,
故选:.
二、填空题(每题5分,共20分)
13.在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个,取得两个红玻璃球的概率为,取得两个绿玻璃球的概率为,则取得两个同颜色的玻璃球的概率为________;至少取得一个红玻璃球的概率为________.
【来源】专题10.4随机事件的概率(练)-《2020年高考一轮复习讲练测》
【答案】
【解析】取得两个同颜色的玻璃球包括两个红玻璃球或两个绿玻璃球故取得两个同颜色的玻璃球的概率;
“至少取得一个红玻璃球”的对立事件是“取得两个绿玻璃球”
故至少取得一个红玻璃球的概率
故答案为:;
14.有以下说法:
①一年按365天计算,两名学生的生日相同的概率是;②买彩票中奖的概率为0.001,那么买1 000张彩票就一定能中奖;③乒乓球赛前,决定谁先发球,抽签方法是从1~10共10个数字中各抽取1个,再比较大小,这种抽签方法是公平的;④昨天没有下雨,则说明“昨天气象局的天气预报降水概率是90%”是错误的.
根据我们所学的概率知识,其中说法正确的序号是___.
【来源】人教B版高中数学必修三同步测试:模块复习课3 概率
【答案】①③
【解析】根据“概率的意义”求解,买彩票中奖的概率0.001,并不意味着买1 000张彩票一定能中奖,只有当买彩票的数量非常大时,我们可以看成大量买彩票的重复试验,中奖的次数为;
昨天气象局的天气预报降水概率是90%,是指可能性非常大,并不一定会下雨.
说法②④是错误的,而利用概率知识可知①③是正确的.
故答案为①③.
15.①某人射击一次,中靶;②从一副牌中抽到红桃A;③种下一粒种子发芽;④掷一枚骰子,出现6点.其中是随机现象的是_____.
【来源】人教B版高中数学必修三同步测试:3.1.1-3.1.2 随机现象 事件与基本事件空间
【答案】①②③④
【解析】根据随机现象的定义知①②③④是随机现象,故填①②③④.
16.从1,2,3,4,5这5个数中任取两个数,其中:
①恰有一个是偶数和恰有一个是奇数;
②至少有一个是奇数和两个都是奇数;
③至少有一个是奇数和两个都是偶数;
④至少有一个是奇数和至少有一个是偶数.
上述事件中,是对立事件的是________.
【来源】陕西省宝鸡市金台区2019-2020学年高三教学质量检测数学文试题
【答案】③
【解析】①恰有一个是偶数和恰有一个是奇数不是互斥事件,也不是对立事件;
②至少有一个是奇数和两个都是奇数不是互斥事件,也不是对立事件;
③至少有一个是奇数和两个都是偶数是互斥事件,也是对立事件;
④至少有一个是奇数和至少有一个是偶数不是互斥事件,也不是对立事件;
故答案为:③
三、解答题(17题10分,其余12分,共70分)
17.某单位利用“学习强国”平台,开展网上学习,实行积分制.为了了解积分情况,随机调查了名员工,得到这些员工学习得分频数分布表:
得分
人数
(Ⅰ)求这些员工学习得分的平均数(同一组中的数据用该组区间的中点值为代表);
(Ⅱ)用分层抽样的方法从得分在和的员工中选取人.从选取的人中,再任选取人,求得分在和中各有人的概率.
【来源】2020届陕西省咸阳市高三上学期期末考试数学(文)试题
【答案】(Ⅰ);(Ⅱ).
【解析】(Ⅰ)记这名员工学习得分的平均数为,
则;
(Ⅱ)用分层抽样可知从中选人,记这人分别为、,
从中选人,记这人分别为、、.
从、、、、中再任取人的情况有:
、、、、、、、、、,共种.
其中得分在和中各有人的情况有:
、、、、、,共种.
记事件为“得分在和中各有人”,则.
18.某超市随机选取位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
甲 乙 丙 丁
√ × √ √
× √ × √
√ √ √ ×
√ × √ ×
85 √ × × ×
× √ × ×
(1)估计顾客同时购买乙和丙的概率;
(2)估计顾客在甲、乙、丙、丁中同时购买中商品的概率;
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
【来源】北京十二中2016-2017学年下学期高二期中试卷 数学(文科)
【答案】(1)0.2;(2)0.3;(3)丙
【解析】 (1)从统计表可以看出,在这1 000位顾客中有200位顾客同时购买了乙和丙,所以顾客同时购买乙和丙的概率可以估计为=0.2.
(2)从统计表可以看出,在这1 000位顾客中,有100位顾客同时购买了甲、丙、丁,另有200位顾客同时购买了甲、乙、丙,其他顾客最多购买了2种商品.
所以顾客在甲、乙、丙、丁中同时购买3种商品的概率可以估计为=0.3.
(3)与(1)同理,可得:顾客同时购买甲和乙的概率可以估计为=0.2,顾客同时购买甲和丙的概率可以估计为=0.6,顾客同时购买甲和丁的概率可以估计为=0.1.所以,如果顾客购买了甲,则该顾客同时购买丙的可能性最大.
19.某班选派5人,参加学校举行的数学竞赛,获奖的人数及其概率如下:
获奖人数 0 1 2 3 4 5
概率 0.1 0.16 x y 0.2 z
(1)若获奖人数不超过2人的概率为0.56,求x的值;
(2)若获奖人数最多4人的概率为0.96,最少3人的概率为0.44,求y,z的值.
【来源】专题10.7第十章 统计与统计案例、概率(单元测试)(测)-《2020年高考一轮复习讲练测》
【答案】(1) 0.3;(2) y=0.2, z=0.04.
【解析】记事件“在竞赛中,有k人获奖”为Ak(k∈N,k≤5),则事件Ak彼此互斥.
(1)∵获奖人数不超过2人的概率为0.56,
∴P(A0)+P(A1)+P(A2)=0.1+0.16+x=0.56.
解得x=0.3.
(2)由获奖人数最多4人的概率为0.96,得P(A5)=1-0.96=0.04,即z=0.04.
由获奖人数最少3人的概率为0.44,得P(A3)+P(A4)+P(A5)=0.44,即y+0.2+0.04=0.44.
解得y=0.2.
20.我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
(1)根据频率分布直方图估算P的平均值;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
【来源】2020届四川省达州市普通高中高三第一次诊断性测试数学(文)试题
【答案】(1)48 (2)
【解析】(1)根据频率分布直方图估算的平均值:
.
(2)该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,
从这4户中随机抽取2户,
基本事件总数,
这2户值的和超过100元包含的基本事件有,,,,共4个,
这2户值的和超过100元的概率.
21.智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从名手机使用者中随机抽取名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: ,.
(1)根据频率分布直方图,估计这名手机使用者中使用时间的中位数是多少分钟 (精确到整数)
(2)估计手机使用者平均每天使用手机多少分钟 (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的名手机使用者中在和中按比例分别抽取人和人组成研究小组,然后再从研究小组中选出名组长.求这名组长分别选自和的概率是多少?
【来源】辽宁省锦州市2018-2019学年高一下学期期末数学试题
【答案】(1) 分钟. (2)58分钟;(3)
【解析】(1)设中位数为,则
解得:(分钟)
这名手机使用者中使用时间的中位数是分钟
(2)平均每天使用手机时间为:(分钟)
即手机使用者平均每天使用手机时间为分钟
(3)设在内抽取的两人分别为,在内抽取的三人分别为,
则从五人中选出两人共有以下种情况:
两名组长分别选自和的共有以下种情况:
所求概率
22.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型 第一类 第二类 第三类 第四类 第五类 第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
【来源】2018年全国普通高等学校招生统一考试文科数学(北京卷)
【答案】(Ⅰ);(Ⅱ);(Ⅲ)增加第五类电影的好评率,减少第二类电影的好评率.
【解析】(Ⅰ)由题意知,样本中电影的总部数是,
第四类电影中获得好评的电影部数是,
故所求概率为;
(Ⅱ)设“随机选取部电影,这部电影没有获得好评”为事件B.
没有获得好评的电影共有部,
由古典概型概率公式得;
(Ⅲ)增加第五类电影的好评率, 减少第二类电影的好评率.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
