整式的乘除---单项式乘以单项式[上学期]
文档属性
| 名称 | 整式的乘除---单项式乘以单项式[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 466.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-30 00:00:00 | ||
图片预览








文档简介
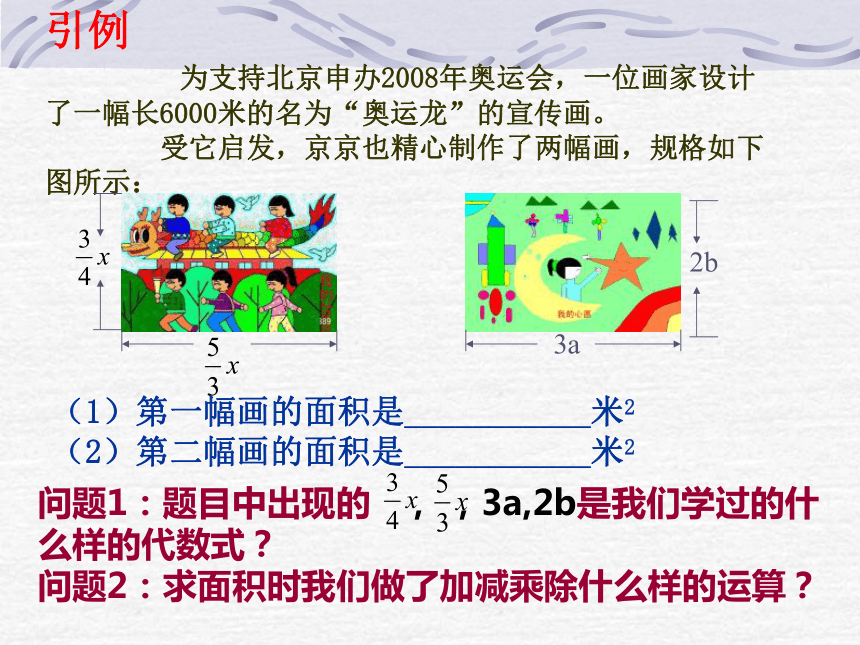
课件24张PPT。引例
为支持北京申办2008年奥运会,一位画家设计了一幅长6000米的名为“奥运龙”的宣传画。
受它启发,京京也精心制作了两幅画,规格如下图所示:(1)第一幅画的面积是___________米2
(2)第二幅画的面积是___________米2问题1:题目中出现的 , ,3a,2b是我们学过的什么样的代数式?
问题2:求面积时我们做了加减乘除什么样的运算?
(2×5)(-4 ×5)[(-2) ×(-3) ]试一试=10x5=-20x3y2=6x3y2你能从这里总结出怎样进行单项式乘以单项式吗?(同位或前后位互相讨论一下)·(x3·x2)·(x2·x)·(y·y)·(x2·x)·y22b·3a=(2×3)=6ab·b·a(1)系数相乘(2)相同字母的幂相乘
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式。
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。单项式乘以单项式法则:快速抢答!
判断正误(如果不对应如何改正?)
(1)4a3·2a2=8a6 ( )
(2)2x4·3x4=5x8 ( )
(3)-6x2·3xy=18x3y ( )
(4)(-2ab2)(-3abc)=-6a2b3 ( )×× ××例1:计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)比一比看谁做的有快又准!
3a2·(-2a3)
(-3x2y)·(-4y2z)
(3)
=[3×(-2)]·(a2·a3) =-6a5=[(-3)·(-4)]·x2·(y·y2)·z=12x2y3z请同学们自已编一道单项式乘以单项式的题目,同位互相换过来做一做,做完之后再换过来互相检查一下。例2 计算
(-2a2)3 ·(-3a3)2
观察一下,例2比例1多了什么运算?例1 计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)(1)先做乘方,再做单项式相乘。(2)系数相乘不要漏掉负号讨论解答:遇到积的乘方怎么办?运算时应先算什么?(同位或前后位讨论一下)试一试!
计算
我们可以用单项式乘以单项式来解决许多生活中的实际问题 ,例如例3:
卫星绕地球运动的速度(即第一宇宙速度)约为7.9 ×103米/秒,则卫星运行3 ×102秒所走的路程约是多少?1、光速约为3 ×108米/秒,太阳光射到地球上的时间约为5 ×102秒,则地球与太阳的距离约是多少米?
2、小明的步长为a米,他量得客厅长15步,宽14步,请问小明家客厅有多少平方米?试一试,你能行!如果a·a可以看做是边长为a的正方形的面积,那么你会说明3a·2b, 3a·5a·b的几何意义吗?探究·讨论aaa·a的几何意义:a·a可以看作边长是a的正方形的面积单项式相乘的几何意义探究·讨论如果a·a可以看做是边长为a的正方形的面积,那么你会说明3a·2b, 3a·5a·b的几何意义吗?3a·2b3a·5a·b 3a·5a·b的几何意义: 3a·5a·b可以看作长是5a ,宽是b,高是3a的长方体的体积.1.这节课你有什么样的收获?
2.还有哪些疑问?讨论(1)单项式乘以单项式的法则(2)单项式乘以单项式幂的乘法运算小结(3)可以用单项式乘以单项式来解决现实生活中的问题作业布置:
必做题:
P80第1题
看谁更聪明,试一试!
P80第2题
动手实践一下!
用12块边长为a的正方形纸片拼成一个长方形,并用不同的方法表示你所拼出来的长方形的面积。从不同的表示方法中,你能得到什么结论?你有几种不同的拼法?在每种拼法中你都能得到类似的结论吗?探索题234511211109876用12块边长为a的正方形纸片拼成一个长方形。有几种不同的拼法?请你找出来。探究性作业234511211109876234511211109876(1)234511211109876234516121110987234511211109876(1)(2)234511211109876234516121110987231458761211109234511211109876(1)(2)(3)祝同学们学习愉快!
为支持北京申办2008年奥运会,一位画家设计了一幅长6000米的名为“奥运龙”的宣传画。
受它启发,京京也精心制作了两幅画,规格如下图所示:(1)第一幅画的面积是___________米2
(2)第二幅画的面积是___________米2问题1:题目中出现的 , ,3a,2b是我们学过的什么样的代数式?
问题2:求面积时我们做了加减乘除什么样的运算?
(2×5)(-4 ×5)[(-2) ×(-3) ]试一试=10x5=-20x3y2=6x3y2你能从这里总结出怎样进行单项式乘以单项式吗?(同位或前后位互相讨论一下)·(x3·x2)·(x2·x)·(y·y)·(x2·x)·y22b·3a=(2×3)=6ab·b·a(1)系数相乘(2)相同字母的幂相乘
(3)只在一个单项式中出
现的字母,则连同它的
指数一起作为积的一个
因式。
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式中出现的字母,则连同它的指数一起作为积的一个因式。单项式乘以单项式法则:快速抢答!
判断正误(如果不对应如何改正?)
(1)4a3·2a2=8a6 ( )
(2)2x4·3x4=5x8 ( )
(3)-6x2·3xy=18x3y ( )
(4)(-2ab2)(-3abc)=-6a2b3 ( )×× ××例1:计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)比一比看谁做的有快又准!
3a2·(-2a3)
(-3x2y)·(-4y2z)
(3)
=[3×(-2)]·(a2·a3) =-6a5=[(-3)·(-4)]·x2·(y·y2)·z=12x2y3z请同学们自已编一道单项式乘以单项式的题目,同位互相换过来做一做,做完之后再换过来互相检查一下。例2 计算
(-2a2)3 ·(-3a3)2
观察一下,例2比例1多了什么运算?例1 计算
(1) 3x2y·(-2xy3)
(2) (-5a2b3)·(-4b2c)(1)先做乘方,再做单项式相乘。(2)系数相乘不要漏掉负号讨论解答:遇到积的乘方怎么办?运算时应先算什么?(同位或前后位讨论一下)试一试!
计算
我们可以用单项式乘以单项式来解决许多生活中的实际问题 ,例如例3:
卫星绕地球运动的速度(即第一宇宙速度)约为7.9 ×103米/秒,则卫星运行3 ×102秒所走的路程约是多少?1、光速约为3 ×108米/秒,太阳光射到地球上的时间约为5 ×102秒,则地球与太阳的距离约是多少米?
2、小明的步长为a米,他量得客厅长15步,宽14步,请问小明家客厅有多少平方米?试一试,你能行!如果a·a可以看做是边长为a的正方形的面积,那么你会说明3a·2b, 3a·5a·b的几何意义吗?探究·讨论aaa·a的几何意义:a·a可以看作边长是a的正方形的面积单项式相乘的几何意义探究·讨论如果a·a可以看做是边长为a的正方形的面积,那么你会说明3a·2b, 3a·5a·b的几何意义吗?3a·2b3a·5a·b 3a·5a·b的几何意义: 3a·5a·b可以看作长是5a ,宽是b,高是3a的长方体的体积.1.这节课你有什么样的收获?
2.还有哪些疑问?讨论(1)单项式乘以单项式的法则(2)单项式乘以单项式幂的乘法运算小结(3)可以用单项式乘以单项式来解决现实生活中的问题作业布置:
必做题:
P80第1题
看谁更聪明,试一试!
P80第2题
动手实践一下!
用12块边长为a的正方形纸片拼成一个长方形,并用不同的方法表示你所拼出来的长方形的面积。从不同的表示方法中,你能得到什么结论?你有几种不同的拼法?在每种拼法中你都能得到类似的结论吗?探索题234511211109876用12块边长为a的正方形纸片拼成一个长方形。有几种不同的拼法?请你找出来。探究性作业234511211109876234511211109876(1)234511211109876234516121110987234511211109876(1)(2)234511211109876234516121110987231458761211109234511211109876(1)(2)(3)祝同学们学习愉快!
