【核心素养目标】5.4应用二元一次方程 教学设计
文档属性
| 名称 | 【核心素养目标】5.4应用二元一次方程 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 894.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-06 09:09:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
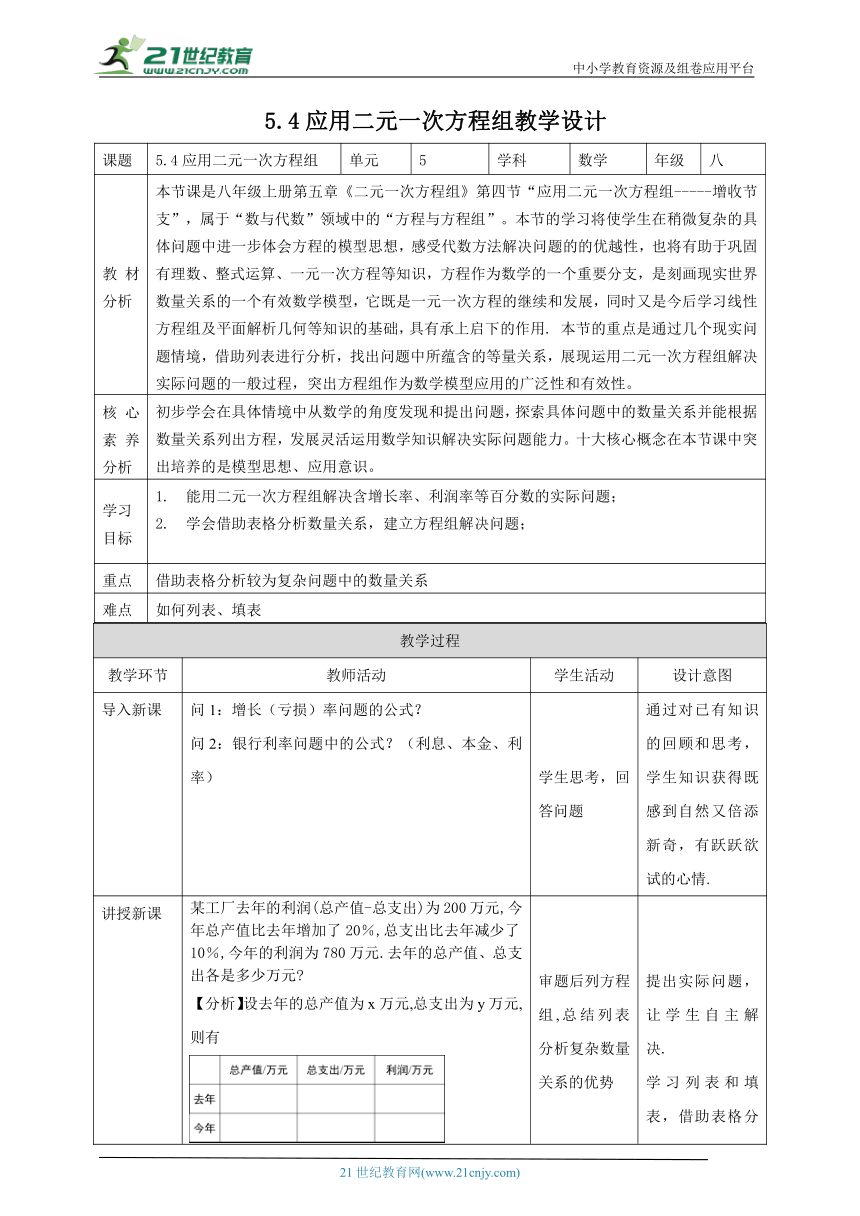
5.4应用二元一次方程组教学设计
课题 5.4应用二元一次方程组 单元 5 学科 数学 年级 八
教材分析 本节课是八年级上册第五章《二元一次方程组》第四节“应用二元一次方程组-----增收节支”,属于“数与代数”领域中的“方程与方程组”。本节的学习将使学生在稍微复杂的具体问题中进一步体会方程的模型思想,感受代数方法解决问题的的优越性,也将有助于巩固有理数、整式运算、一元一次方程等知识,方程作为数学的一个重要分支,是刻画现实世界数量关系的一个有效数学模型,它既是一元一次方程的继续和发展,同时又是今后学习线性方程组及平面解析几何等知识的基础,具有承上启下的作用. 本节的重点是通过几个现实问题情境,借助列表进行分析,找出问题中所蕴含的等量关系,展现运用二元一次方程组解决实际问题的一般过程,突出方程组作为数学模型应用的广泛性和有效性。
核心素养分析 初步学会在具体情境中从数学的角度发现和提出问题,探索具体问题中的数量关系并能根据数量关系列出方程,发展灵活运用数学知识解决实际问题能力。十大核心概念在本节课中突出培养的是模型思想、应用意识。
学习 目标 1. 能用二元一次方程组解决含增长率、利润率等百分数的实际问题; 2. 学会借助表格分析数量关系,建立方程组解决问题;
重点 借助表格分析较为复杂问题中的数量关系
难点 如何列表、填表
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 问1:增长(亏损)率问题的公式? 问2:银行利率问题中的公式?(利息、本金、利率) 学生思考,回答问题 通过对已有知识的回顾和思考,学生知识获得既感到自然又倍添新奇,有跃跃欲试的心情.
讲授新课 某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元 【分析】设去年的总产值为x万元,总支出为y万元,则有 审题: 找等量关系: 解:设去年的总产值为x万元,总支出为y万元,则有 解得: 答:去年的总产值是2 000万元,总支出是1800万元. 技巧: 1.图表分析有利于理清题中的未知量,已知量以及等量关系,条理清楚. 2.借助方程组解决实际问题. 典例精析: 例、医院用甲、乙两种原料为手术后的病人配制营养品.每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质.若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰好满足病人的需要? 设每餐需要甲、乙两种原料各x,y克,则有下表 解:设每餐需要甲、乙两种原料各x克,y克, 根据题意可得 解得 答:每餐需甲原料28克,乙原料30克. 审题后列方程组,总结列表分析复杂数量关系的优势 借助表格分析问题,解决问题 提出实际问题,让学生自主解决. 学习列表和填表,借助表格分析数量关系,通过对比感受列表分析的便捷性. 充分感受解决数量关系复杂的实际问题,列表分析的优势,进而提高分析问题的能力和学习兴趣
课堂练习 1.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲、乙两种商品原来的单价分别为x元、y元,则下列方程组正确的是 ( ) A B C . D . 2.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( ) A. B. C. D. 3.学校去年有学生3 100名,今年比去年增加4.4% ,其中寄宿学生增加了6% ,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x名,走读学生y名,则可列出方程组为: 。 4.某公司购买甲、乙两种货物,设甲、乙两种货物的进货价分别为x元和y元.若已知两种货物的进货价共30000元,则可列方程______________;若共获利3150元,已知甲种货物的利润率是10%,乙种货物的利润率是11%,则可列方程__________________ ,由此可得方程组__________________. 5.某人以两种形式存8000元,一种储蓄的年利率为10%,另一种储蓄的年利率为11%.一年到期后,他共得利息855元(没有利息税),问两种储蓄他各存了多少钱 学生课堂练习,然后上台演示自己的答案。 学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:5.4应用二元一次方程组 1.一般步骤:审、设、列、解、验、答 2.找等量关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.4应用二元一次方程组教学设计
课题 5.4应用二元一次方程组 单元 5 学科 数学 年级 八
教材分析 本节课是八年级上册第五章《二元一次方程组》第四节“应用二元一次方程组-----增收节支”,属于“数与代数”领域中的“方程与方程组”。本节的学习将使学生在稍微复杂的具体问题中进一步体会方程的模型思想,感受代数方法解决问题的的优越性,也将有助于巩固有理数、整式运算、一元一次方程等知识,方程作为数学的一个重要分支,是刻画现实世界数量关系的一个有效数学模型,它既是一元一次方程的继续和发展,同时又是今后学习线性方程组及平面解析几何等知识的基础,具有承上启下的作用. 本节的重点是通过几个现实问题情境,借助列表进行分析,找出问题中所蕴含的等量关系,展现运用二元一次方程组解决实际问题的一般过程,突出方程组作为数学模型应用的广泛性和有效性。
核心素养分析 初步学会在具体情境中从数学的角度发现和提出问题,探索具体问题中的数量关系并能根据数量关系列出方程,发展灵活运用数学知识解决实际问题能力。十大核心概念在本节课中突出培养的是模型思想、应用意识。
学习 目标 1. 能用二元一次方程组解决含增长率、利润率等百分数的实际问题; 2. 学会借助表格分析数量关系,建立方程组解决问题;
重点 借助表格分析较为复杂问题中的数量关系
难点 如何列表、填表
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 问1:增长(亏损)率问题的公式? 问2:银行利率问题中的公式?(利息、本金、利率) 学生思考,回答问题 通过对已有知识的回顾和思考,学生知识获得既感到自然又倍添新奇,有跃跃欲试的心情.
讲授新课 某工厂去年的利润(总产值-总支出)为200万元,今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.去年的总产值、总支出各是多少万元 【分析】设去年的总产值为x万元,总支出为y万元,则有 审题: 找等量关系: 解:设去年的总产值为x万元,总支出为y万元,则有 解得: 答:去年的总产值是2 000万元,总支出是1800万元. 技巧: 1.图表分析有利于理清题中的未知量,已知量以及等量关系,条理清楚. 2.借助方程组解决实际问题. 典例精析: 例、医院用甲、乙两种原料为手术后的病人配制营养品.每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质.若病人每餐需要35单位蛋白质和40单位铁质,那么每餐甲、乙两种原料各多少克恰好满足病人的需要? 设每餐需要甲、乙两种原料各x,y克,则有下表 解:设每餐需要甲、乙两种原料各x克,y克, 根据题意可得 解得 答:每餐需甲原料28克,乙原料30克. 审题后列方程组,总结列表分析复杂数量关系的优势 借助表格分析问题,解决问题 提出实际问题,让学生自主解决. 学习列表和填表,借助表格分析数量关系,通过对比感受列表分析的便捷性. 充分感受解决数量关系复杂的实际问题,列表分析的优势,进而提高分析问题的能力和学习兴趣
课堂练习 1.甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.若设甲、乙两种商品原来的单价分别为x元、y元,则下列方程组正确的是 ( ) A B C . D . 2.某校春季运动会比赛中,八年级(1)班、(5)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(5)班得分比为6:5;乙同学说:(1)班得分比(5)班得分的2倍少40分.若设(1)班得x分,(5)班得y分,根据题意所列的方程组应为( ) A. B. C. D. 3.学校去年有学生3 100名,今年比去年增加4.4% ,其中寄宿学生增加了6% ,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名?设去年有寄宿学生x名,走读学生y名,则可列出方程组为: 。 4.某公司购买甲、乙两种货物,设甲、乙两种货物的进货价分别为x元和y元.若已知两种货物的进货价共30000元,则可列方程______________;若共获利3150元,已知甲种货物的利润率是10%,乙种货物的利润率是11%,则可列方程__________________ ,由此可得方程组__________________. 5.某人以两种形式存8000元,一种储蓄的年利率为10%,另一种储蓄的年利率为11%.一年到期后,他共得利息855元(没有利息税),问两种储蓄他各存了多少钱 学生课堂练习,然后上台演示自己的答案。 学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:5.4应用二元一次方程组 1.一般步骤:审、设、列、解、验、答 2.找等量关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
