北师大版八年级数学上册6.1.2加权平均数的计算 课件(共25张PPT)
文档属性
| 名称 | 北师大版八年级数学上册6.1.2加权平均数的计算 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 747.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 11:56:34 | ||
图片预览







文档简介
(共25张PPT)
6.1.2 加权平均数的计算
八年级上册
学习目标
1、进一步理解加权平均数的含义,会求实际情境中的加权平均数.
2、体会算术平均数和加权平均数的联系与区别,并能利用他们解决一些实际问题.
3、体会数学与社会生活的密切联系,了解数学的价值,增进对数学的理解和学好数学的信心.
学习重难点
重点
难点
进一步理解加权平均数的含义,会求实际情境中的加权平均数.
体会算术平均数和加权平均数的联系与区别.
上一节课,我们学会求算术平均数和加权平均数。
知识回顾
一般地,对于n个数x1,x2,...,xn,我们把 叫做这n个数的算术平均数,简称平均数,记作 .
练一练1.
在一次数学测试中,小明所在小组的8个同学的成绩(单位:分)分别是95,88,92,90,87,89,94,93,则这组数据的平均分是 .
91分
知识回顾
叫做这n个数的加权平均数.
练一练2.
在某公司的面试中,李明的得分情况为:个人形象89分,工作能力93分,交际能力83分已知个人形象、工作能力和交际能力的权重为2:4:4,则李明的最终成绩是 .
88.2分
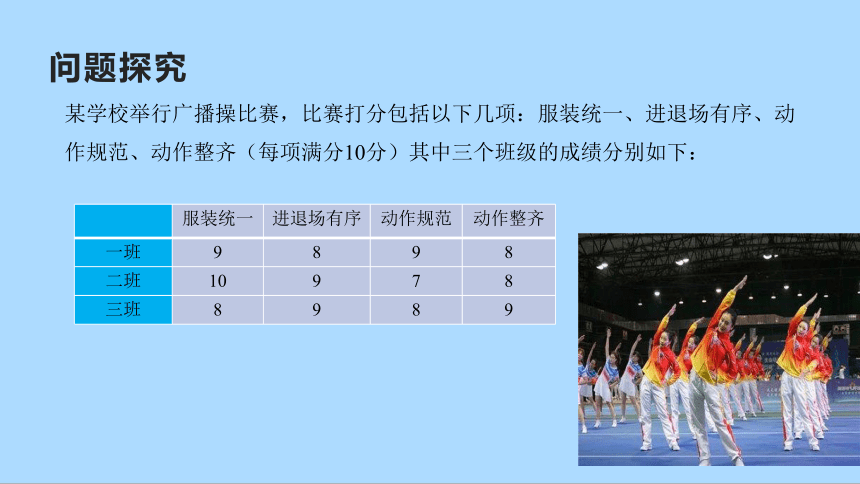
问题探究
某学校举行广播操比赛,比赛打分包括以下几项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分)其中三个班级的成绩分别如下:
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
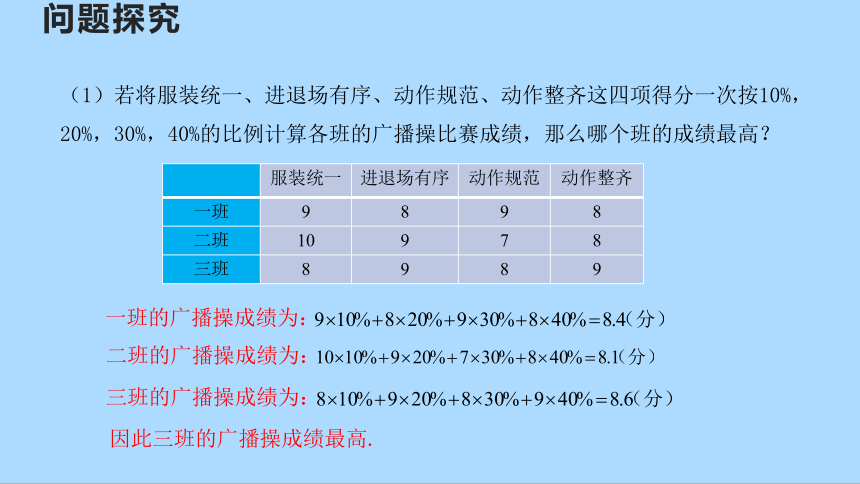
问题探究
(1)若将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此三班的广播操成绩最高.
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
问题探究
(2)你认为上述四项中哪一项更为重要?请你按自己的想法设计一个评分方案,根据你的评分方案,哪一个班的广播操比赛成绩最高?
同学1:我认为动作规范更为重要,将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按10%,10%,50%,30%的比例计算各班的广播操比赛成绩.得到
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此一班的广播操成绩最高.
问题探究
同学2:我认为服装统一更为重要,将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按40%,30%,20%,10%的比例计算各班的广播操比赛成绩.得到
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此二班的广播操成绩最高.
问题总结
利用加权平均数解决应用题时,“权”有差异,得出的结果就会不同,也就是说权的差异对结果有影响。
议一议
1.小明骑自行车的速度是15千米/时,步行的速度是5千米/时。
(1)如果小明先骑自行车1小时,然后又步行了1小时,那么他的平均速度是多少?
(2)如果小明先骑自行车2小时,然后步行了3小时,那么他的平均速度是多少?
解:(1)1小明的平均速度是
(15×1+5×1)÷(1+1)=10(千米/时)
(2)小明的平均速度是
(15×2+5×3)÷(2+3)=9(千米/时)
(3)举出生活中加权平均数的几个实例.
问题探究
同学1:甲、乙、丙三种糖果售价分别为每千克6元、7元、8元,若将甲种8千克、乙种10千克、丙种2千克混在一起,则售价应定为每千克6.7元.
问题探究
同学2:某次歌咏比赛中,选手张华的唱功、音乐常识、综合知识分别得了90分、80分、85分,若这三项按5∶3∶2的比例计算平均分,则张华的平均分是86分.
问题探究
同学3:某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试成绩占60%.小海这个学期的期中、期末体育成绩(百分制)分别是80分,90分,则小海这个学期的体育综合成绩是86分.
方法总结
加权平均数的常见形式:
3、百分比:如 30%、30%、20%和20%
2、比:如 3:3:2:2.
1、频数:如 2,4,4.
B
课堂练习
1.某校调查了20名同学某一周玩手机游戏的次数,调查结果如下表所示,那么这20名同学玩手机游戏次数的平均数为( )
A.5 B.5.5 C.6 D.6.5
次数 2 4 5 8
人数 2 2 10 6
课堂练习
2.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树_______棵.
4
3.某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按2:4:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是94分,91分和94分,则他本学期数学学期综合成绩是______分.
课堂练习
92.8
课堂练习
4.面试时,某人的基本知识、表达能力、工作态度的得分分别是80分,70分,85分,若依次按30%,30%,40%的比例确定成绩,则这个人的面试成绩是多少?
答:这个人的面试成绩是79分.
解:面试成绩=80×30%+70×30%+85×40%=79(分)
课堂练习
5.某学校欲招一名语文教师,对甲、乙、丙三名候选人进行了三项素质测试,她们的各项测试成绩如表所示:
测试项目 测试成绩 甲 乙 丙
课堂教学 74 87 69
普通话 58 74 70
粉笔字 87 43 65
则学校将课堂教学、普通话和粉笔字三项测试得分按50%∶30%∶20%的比例确定各人的测试成绩,此时谁将被录用?
解:甲的成绩=74×50%+58×30%+87×20%=71.8(分)
乙的成绩=87×50%+74×30%+43×20%=74.3(分)
丙的成绩=69×50%+70×30%+65×20%=68.5(分)
答:乙将会被录取.
课堂总结
权的常见形式
算术平均数与加权平均数有哪些联系与区别
1、频数:如 2,4,4.
2、比:如 3:3:2:2.
3、百分比:如 30%、30%、和20%
联系:算术平均数是加权平均数各项的权都相等
的一种特殊情况,即算术平均数是加权平均数,而
加权平均数不一定是算术平均数。
区别:由于权的不同,导致结果不同,故权的差异对结果有影响。
课后作业
1、在A,B,C,D四块实验田进行水稻新品种种植实验,各块实验田的面积和所种水稻的单位产量如下表:
则这四块实验田中水稻的平均单位产量是多少?
A B C D
单位产量/(kg/hm2 ) 8250 7875 7125 6375
面积//hm2 4 3 1 2
课后作业
2、某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙进行了初步测试,测试成绩如下表.
(1)如果将学历、经验和工作态度三项得分按1:2:2的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者?说说理由.
甲 乙 丙
学历 7 9 8
经验 8 7 7
工作态度 6 8 5
课后作业
3、某学校对各个班级的教室卫生情况的检查包括以下几项,黑板、门窗、桌椅、地面.一天,三个班级的各项卫生成绩(单位;分)分别如下:
(1)小明将黑板、门窗、桌椅、地面这四项得分依次按15%、10%、35%、40%的比例计算各班的卫生成绩,那么哪个班的成绩最高?
(2)你认为上述四项中,哪一项更为重要请你按自己的想法设计一个评分方案,根据你的方案,哪一个班的卫生成绩最高?
黑板 门窗 桌椅 地面
一班 95 90 90 86
二班 90 95 85 90
三班 85 90 95 90
再 见
6.1.2 加权平均数的计算
八年级上册
学习目标
1、进一步理解加权平均数的含义,会求实际情境中的加权平均数.
2、体会算术平均数和加权平均数的联系与区别,并能利用他们解决一些实际问题.
3、体会数学与社会生活的密切联系,了解数学的价值,增进对数学的理解和学好数学的信心.
学习重难点
重点
难点
进一步理解加权平均数的含义,会求实际情境中的加权平均数.
体会算术平均数和加权平均数的联系与区别.
上一节课,我们学会求算术平均数和加权平均数。
知识回顾
一般地,对于n个数x1,x2,...,xn,我们把 叫做这n个数的算术平均数,简称平均数,记作 .
练一练1.
在一次数学测试中,小明所在小组的8个同学的成绩(单位:分)分别是95,88,92,90,87,89,94,93,则这组数据的平均分是 .
91分
知识回顾
叫做这n个数的加权平均数.
练一练2.
在某公司的面试中,李明的得分情况为:个人形象89分,工作能力93分,交际能力83分已知个人形象、工作能力和交际能力的权重为2:4:4,则李明的最终成绩是 .
88.2分
问题探究
某学校举行广播操比赛,比赛打分包括以下几项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分)其中三个班级的成绩分别如下:
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
问题探究
(1)若将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按10%,20%,30%,40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此三班的广播操成绩最高.
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
问题探究
(2)你认为上述四项中哪一项更为重要?请你按自己的想法设计一个评分方案,根据你的评分方案,哪一个班的广播操比赛成绩最高?
同学1:我认为动作规范更为重要,将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按10%,10%,50%,30%的比例计算各班的广播操比赛成绩.得到
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此一班的广播操成绩最高.
问题探究
同学2:我认为服装统一更为重要,将服装统一、进退场有序、动作规范、动作整齐这四项得分一次按40%,30%,20%,10%的比例计算各班的广播操比赛成绩.得到
一班的广播操成绩为:
二班的广播操成绩为:
三班的广播操成绩为:
因此二班的广播操成绩最高.
问题总结
利用加权平均数解决应用题时,“权”有差异,得出的结果就会不同,也就是说权的差异对结果有影响。
议一议
1.小明骑自行车的速度是15千米/时,步行的速度是5千米/时。
(1)如果小明先骑自行车1小时,然后又步行了1小时,那么他的平均速度是多少?
(2)如果小明先骑自行车2小时,然后步行了3小时,那么他的平均速度是多少?
解:(1)1小明的平均速度是
(15×1+5×1)÷(1+1)=10(千米/时)
(2)小明的平均速度是
(15×2+5×3)÷(2+3)=9(千米/时)
(3)举出生活中加权平均数的几个实例.
问题探究
同学1:甲、乙、丙三种糖果售价分别为每千克6元、7元、8元,若将甲种8千克、乙种10千克、丙种2千克混在一起,则售价应定为每千克6.7元.
问题探究
同学2:某次歌咏比赛中,选手张华的唱功、音乐常识、综合知识分别得了90分、80分、85分,若这三项按5∶3∶2的比例计算平均分,则张华的平均分是86分.
问题探究
同学3:某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占40%,期末考试成绩占60%.小海这个学期的期中、期末体育成绩(百分制)分别是80分,90分,则小海这个学期的体育综合成绩是86分.
方法总结
加权平均数的常见形式:
3、百分比:如 30%、30%、20%和20%
2、比:如 3:3:2:2.
1、频数:如 2,4,4.
B
课堂练习
1.某校调查了20名同学某一周玩手机游戏的次数,调查结果如下表所示,那么这20名同学玩手机游戏次数的平均数为( )
A.5 B.5.5 C.6 D.6.5
次数 2 4 5 8
人数 2 2 10 6
课堂练习
2.某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
植树棵数 3 4 5 6
人数 20 15 10 5
那么这50名学生平均每人植树_______棵.
4
3.某校规定:学生的数学学期综合成绩是由平时、期中和期末三项成绩按2:4:4的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是94分,91分和94分,则他本学期数学学期综合成绩是______分.
课堂练习
92.8
课堂练习
4.面试时,某人的基本知识、表达能力、工作态度的得分分别是80分,70分,85分,若依次按30%,30%,40%的比例确定成绩,则这个人的面试成绩是多少?
答:这个人的面试成绩是79分.
解:面试成绩=80×30%+70×30%+85×40%=79(分)
课堂练习
5.某学校欲招一名语文教师,对甲、乙、丙三名候选人进行了三项素质测试,她们的各项测试成绩如表所示:
测试项目 测试成绩 甲 乙 丙
课堂教学 74 87 69
普通话 58 74 70
粉笔字 87 43 65
则学校将课堂教学、普通话和粉笔字三项测试得分按50%∶30%∶20%的比例确定各人的测试成绩,此时谁将被录用?
解:甲的成绩=74×50%+58×30%+87×20%=71.8(分)
乙的成绩=87×50%+74×30%+43×20%=74.3(分)
丙的成绩=69×50%+70×30%+65×20%=68.5(分)
答:乙将会被录取.
课堂总结
权的常见形式
算术平均数与加权平均数有哪些联系与区别
1、频数:如 2,4,4.
2、比:如 3:3:2:2.
3、百分比:如 30%、30%、和20%
联系:算术平均数是加权平均数各项的权都相等
的一种特殊情况,即算术平均数是加权平均数,而
加权平均数不一定是算术平均数。
区别:由于权的不同,导致结果不同,故权的差异对结果有影响。
课后作业
1、在A,B,C,D四块实验田进行水稻新品种种植实验,各块实验田的面积和所种水稻的单位产量如下表:
则这四块实验田中水稻的平均单位产量是多少?
A B C D
单位产量/(kg/hm2 ) 8250 7875 7125 6375
面积//hm2 4 3 1 2
课后作业
2、某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙进行了初步测试,测试成绩如下表.
(1)如果将学历、经验和工作态度三项得分按1:2:2的比例确定各人的最终得分,并以此为据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者?说说理由.
甲 乙 丙
学历 7 9 8
经验 8 7 7
工作态度 6 8 5
课后作业
3、某学校对各个班级的教室卫生情况的检查包括以下几项,黑板、门窗、桌椅、地面.一天,三个班级的各项卫生成绩(单位;分)分别如下:
(1)小明将黑板、门窗、桌椅、地面这四项得分依次按15%、10%、35%、40%的比例计算各班的卫生成绩,那么哪个班的成绩最高?
(2)你认为上述四项中,哪一项更为重要请你按自己的想法设计一个评分方案,根据你的方案,哪一个班的卫生成绩最高?
黑板 门窗 桌椅 地面
一班 95 90 90 86
二班 90 95 85 90
三班 85 90 95 90
再 见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
