粤教版(2019) 必修1 数据与计算 进制转换 课件(15PPT)
文档属性
| 名称 | 粤教版(2019) 必修1 数据与计算 进制转换 课件(15PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
XXXXX学校
进制转换
作者:XXX
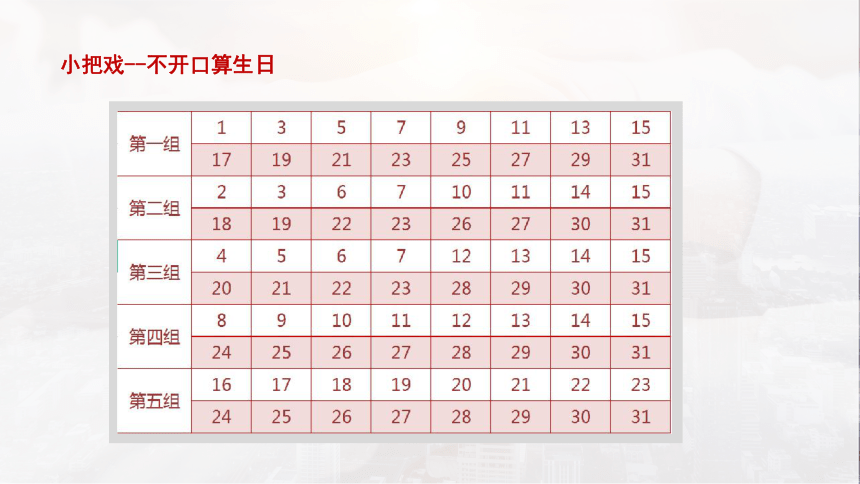
小把戏--不开口算生日
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
第一部分
初识进制
第一部分
初识进制
生活总常见的进制
十进制--逢十进一
七进制--7天为一周
十二进制--12月为一年
二十四进制--24小时为一天
六十进制--60秒一分钟...
...
二进制 - -计算机内部进制
八进制 - -计算机常用进制
十六进制--计算机常用进制
(1)技术实现简单:计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示
第一部分
初识进制
(2)运算规则简单:与十进制数相比,二进制数的运算规则要简单得多,这不仅可以使运算器的结构得到简化,而且有利于提高运算速度
计算机内部采用二进制的主要原因:
(4)易于进行转换:二进制与十进制数易于互相转换
(3)适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
第一部分
初识进制
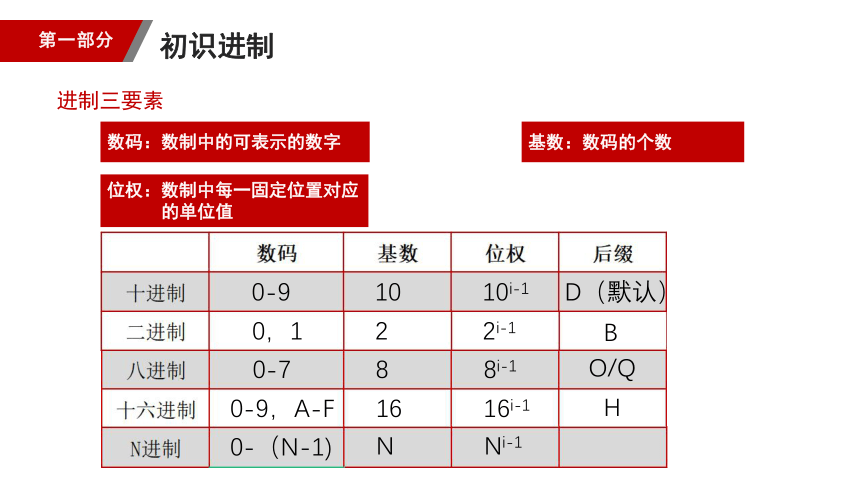
数码:数制中的可表示的数字
位权:数制中每一固定位置对应
的单位值
基数:数码的个数
进制三要素
0-9
10
10i-1
D(默认)
0,1
2
2i-1
B
0-7
8
8i-1
O/Q
0-9,A-F
16
16i-1
H
0-(N-1)
N
Ni-1
第二部分
进制转换
N转十:按权相加法
以10作为中转站
十转N:除以N取余倒序法
转换规律
第二部分
进制转换
十转N:除以N取余倒序法
10进制 2/8/16进制
(22)10 ( )2
22
2
11
0
2
5
1
2
2
1
2
0
10110
1
2
0
1
0
(35)10 ( )2
(35)10 ( )8
(35)10 ( )16
100011
43
23
第二部分
进制转换(拓展)
十转N:按位权拆分法
10进制 2/8/16进制
位权:数制中每一固定位置对应的单位值
101-1
104-1
102-1
103-1
105-1
4 0 8
101-1
102-1
103-1
=
4*100+0*100+8*1
第二部分
进制转换(拓展)
十转N:按位权拆分法
10进制 2/8/16进制
位权:数制中每一固定位置对应的单位值
(22)10 ( )2
10110
=1 0 1 1 0
22=
1*16 +0*8 +1*4 +1*2 +0*1
=1*2^4+0*2^3+1*2^2+1*2^1+0*2^0
(22)10 ( )8
26
22=
2*8+6*1
=2*8^1+6*8^0
=2 6
(22)10 ( )16
16
22=
1*16+6*1
=1*16^1+6*16^0
=1 6
第二部分
进制转换
N转十:按权相加法
2/8/16进制 10进制
( 1 0 1 1 0)2 ( )10
22
20
22
24
21
23
=0*20+1*21+1*22+0*23+1*24
=0*1 +1*2 +1*4 +0*8+1*16
=0+2+4+0+16
=(22)10
(101010)2 ( )10
(127)8 ( )10
(A7)16 ( )10
42
167
87
第三部分
进制应用
n位十进制数可以表示 多少 个不同的数字、字符、颜色…
0-9
10
101
0-99
100
102
0-999
1000
103
......
......
10n
10n
第三部分
进制应用
n位二进制数可以表示 多少 个不同的数字、字符、颜色…
0、1
2
21
00、01、10、11
4
22
000、001...111
8
23
......
......
2n
2n
第三部分
进制应用
n位二进制数可以表示 多少 个不同的数字、字符、颜色…
2n
需要多少位二进制数才能表示出最大值31天?
5
3
1
1
0
0
0
第一组没有
第二组有
第三组有
第四组没有
第五组有
20
0
01
1
0
1
22
0
1
1
0
1
24
0
0
0
1
1
25
1
0
0
1
1
...
29
1
0
1
1
1
30
0
1
1
1
1
1
1
0
0
0
0
31
1
1
1
1
1
...
21
1
0
1
0
1
23
1
1
1
0
1
2
0
1
0
0
0
第三部分
进制小结
XXXXX学校
进制转换
作者:XXX
小把戏--不开口算生日
进制也就是进位计数制,是人为定义的带进位的计数方法。对于任何一种进制—N进制,就表示每一位上的数运算时都是逢N进一。
第一部分
初识进制
第一部分
初识进制
生活总常见的进制
十进制--逢十进一
七进制--7天为一周
十二进制--12月为一年
二十四进制--24小时为一天
六十进制--60秒一分钟...
...
二进制 - -计算机内部进制
八进制 - -计算机常用进制
十六进制--计算机常用进制
(1)技术实现简单:计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示
第一部分
初识进制
(2)运算规则简单:与十进制数相比,二进制数的运算规则要简单得多,这不仅可以使运算器的结构得到简化,而且有利于提高运算速度
计算机内部采用二进制的主要原因:
(4)易于进行转换:二进制与十进制数易于互相转换
(3)适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
第一部分
初识进制
数码:数制中的可表示的数字
位权:数制中每一固定位置对应
的单位值
基数:数码的个数
进制三要素
0-9
10
10i-1
D(默认)
0,1
2
2i-1
B
0-7
8
8i-1
O/Q
0-9,A-F
16
16i-1
H
0-(N-1)
N
Ni-1
第二部分
进制转换
N转十:按权相加法
以10作为中转站
十转N:除以N取余倒序法
转换规律
第二部分
进制转换
十转N:除以N取余倒序法
10进制 2/8/16进制
(22)10 ( )2
22
2
11
0
2
5
1
2
2
1
2
0
10110
1
2
0
1
0
(35)10 ( )2
(35)10 ( )8
(35)10 ( )16
100011
43
23
第二部分
进制转换(拓展)
十转N:按位权拆分法
10进制 2/8/16进制
位权:数制中每一固定位置对应的单位值
101-1
104-1
102-1
103-1
105-1
4 0 8
101-1
102-1
103-1
=
4*100+0*100+8*1
第二部分
进制转换(拓展)
十转N:按位权拆分法
10进制 2/8/16进制
位权:数制中每一固定位置对应的单位值
(22)10 ( )2
10110
=1 0 1 1 0
22=
1*16 +0*8 +1*4 +1*2 +0*1
=1*2^4+0*2^3+1*2^2+1*2^1+0*2^0
(22)10 ( )8
26
22=
2*8+6*1
=2*8^1+6*8^0
=2 6
(22)10 ( )16
16
22=
1*16+6*1
=1*16^1+6*16^0
=1 6
第二部分
进制转换
N转十:按权相加法
2/8/16进制 10进制
( 1 0 1 1 0)2 ( )10
22
20
22
24
21
23
=0*20+1*21+1*22+0*23+1*24
=0*1 +1*2 +1*4 +0*8+1*16
=0+2+4+0+16
=(22)10
(101010)2 ( )10
(127)8 ( )10
(A7)16 ( )10
42
167
87
第三部分
进制应用
n位十进制数可以表示 多少 个不同的数字、字符、颜色…
0-9
10
101
0-99
100
102
0-999
1000
103
......
......
10n
10n
第三部分
进制应用
n位二进制数可以表示 多少 个不同的数字、字符、颜色…
0、1
2
21
00、01、10、11
4
22
000、001...111
8
23
......
......
2n
2n
第三部分
进制应用
n位二进制数可以表示 多少 个不同的数字、字符、颜色…
2n
需要多少位二进制数才能表示出最大值31天?
5
3
1
1
0
0
0
第一组没有
第二组有
第三组有
第四组没有
第五组有
20
0
01
1
0
1
22
0
1
1
0
1
24
0
0
0
1
1
25
1
0
0
1
1
...
29
1
0
1
1
1
30
0
1
1
1
1
1
1
0
0
0
0
31
1
1
1
1
1
...
21
1
0
1
0
1
23
1
1
1
0
1
2
0
1
0
0
0
第三部分
进制小结
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
