单项式的乘法[上学期]
图片预览


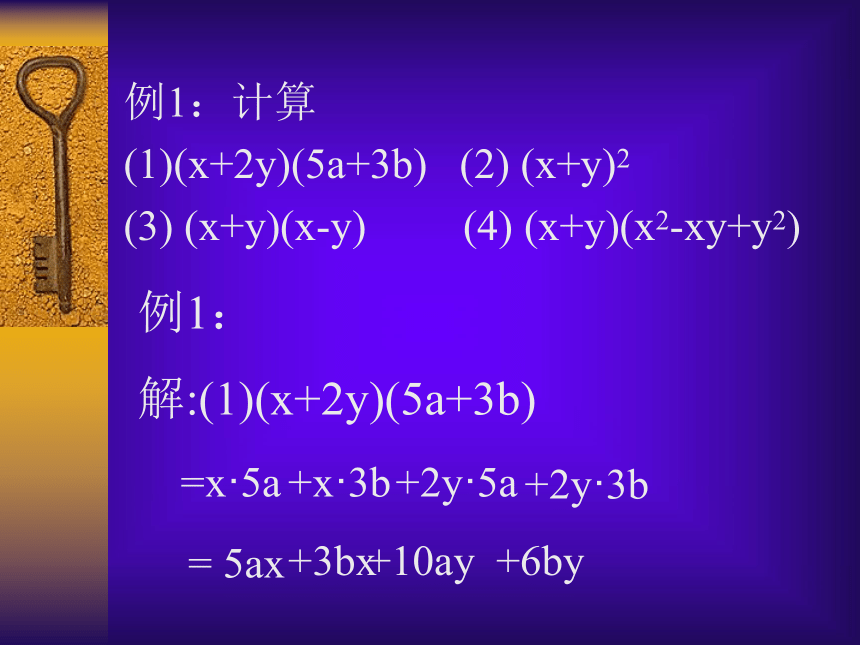
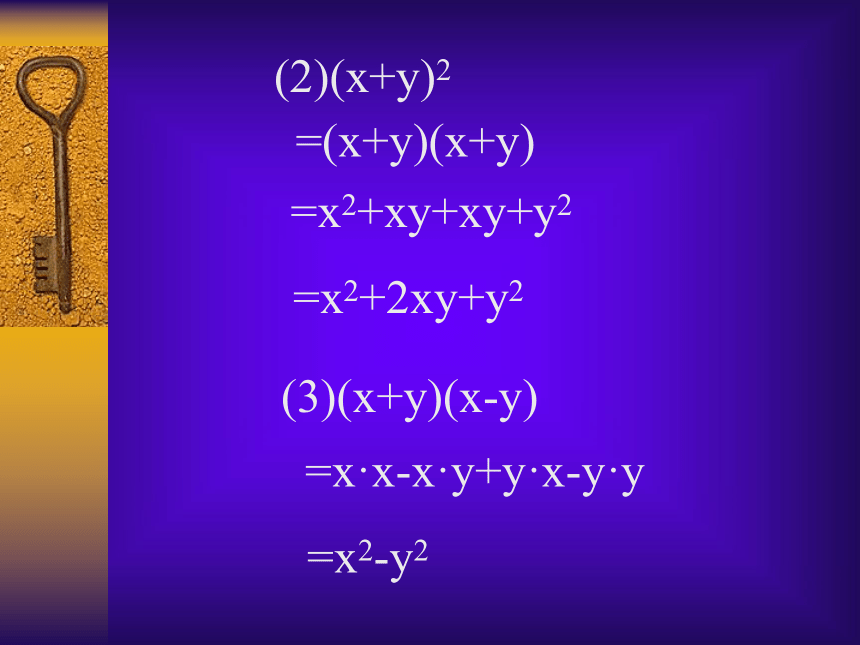
文档简介
课件10张PPT。第五节 多项式的乘法1.单项式与多项式的乘法法则练习:
(1) 3x(-x+y) =2. (a+b)(m+n) =
第2题的特点是什么? -3xy+3xy2
(a+b)(m+n)=?
把(a+b)作为一个整体,利用单项式与多项式的乘法法则:
(a+b)(m+n)
=(a+b)m+(a+b)n
=am+bm+an+bn
=am+an+bm+bn
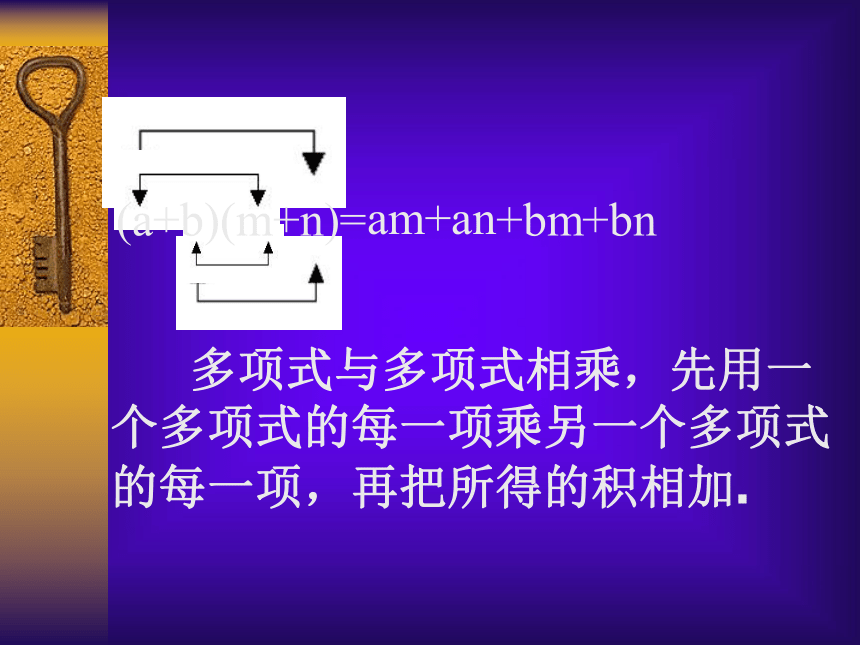
观察:( a+b)(m+n) =am+an+bm+bn的特征am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=例1:计算
(1)(x+2y)(5a+3b) (2) (x+y)2
(3) (x+y)(x-y) (4) (x+y)(x2-xy+y2)例1:
解:(1)(x+2y)(5a+3b)=x·5a +x·3b +2y·5a +2y·3b = 5ax +3bx +10ay +6by (2)(x+y)2=(x+y)(x+y) =x2+xy+xy+y2
=x2+2xy+y2(3)(x+y)(x-y) =x·x-x·y+y·x-y·y
=x2-y2 (4)(x+y)(x2 -xy+y2 ) =x·x2-x·xy+x·y2+y·x2-y·xy+y·y2
=x3-x2y+xy2+yx2-xy2+y3
=x3+y3例2 计算:解:(1)(2)(1)(2)原式原式练习1:
(m+n)(u+v)
(a+b)2
(a-b)2
(4) (8y+5)(8y-5)
(5) (x-y)(x2+xy+y2)
(6) (m+2n)(m-2n)练习2:
(1)(2n+6)(n-3)
(2)(2x+3)(3x-1)
(3)(2a-3b)(a+5b)
(4)(3x-2y)(3x+2y)
(5)(2a+3b)(2a-3b)
(6)(x+y)2
(7)(2a+b)2
(8)(2x+5)2
小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式 相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式想乘的展开式中,有同类项要合并同类项.
(1) 3x(-x+y) =2. (a+b)(m+n) =
第2题的特点是什么? -3xy+3xy2
(a+b)(m+n)=?
把(a+b)作为一个整体,利用单项式与多项式的乘法法则:
(a+b)(m+n)
=(a+b)m+(a+b)n
=am+bm+an+bn
=am+an+bm+bn
观察:( a+b)(m+n) =am+an+bm+bn的特征am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=例1:计算
(1)(x+2y)(5a+3b) (2) (x+y)2
(3) (x+y)(x-y) (4) (x+y)(x2-xy+y2)例1:
解:(1)(x+2y)(5a+3b)=x·5a +x·3b +2y·5a +2y·3b = 5ax +3bx +10ay +6by (2)(x+y)2=(x+y)(x+y) =x2+xy+xy+y2
=x2+2xy+y2(3)(x+y)(x-y) =x·x-x·y+y·x-y·y
=x2-y2 (4)(x+y)(x2 -xy+y2 ) =x·x2-x·xy+x·y2+y·x2-y·xy+y·y2
=x3-x2y+xy2+yx2-xy2+y3
=x3+y3例2 计算:解:(1)(2)(1)(2)原式原式练习1:
(m+n)(u+v)
(a+b)2
(a-b)2
(4) (8y+5)(8y-5)
(5) (x-y)(x2+xy+y2)
(6) (m+2n)(m-2n)练习2:
(1)(2n+6)(n-3)
(2)(2x+3)(3x-1)
(3)(2a-3b)(a+5b)
(4)(3x-2y)(3x+2y)
(5)(2a+3b)(2a-3b)
(6)(x+y)2
(7)(2a+b)2
(8)(2x+5)2
小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式 相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式想乘的展开式中,有同类项要合并同类项.
