人教版选择性必修一 3.2 双向性多解专题(含答案)
文档属性
| 名称 | 人教版选择性必修一 3.2 双向性多解专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 955.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-02 12:28:58 | ||
图片预览


文档简介
人教版选择性必修一第三章双向性多解专题(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,一列简谐横波沿轴传播,时刻与时刻在轴上的区间内的波形相同.下列说法正确的是( )
A. 该波一定沿轴正方向传播 B. 该波的周期一定为
C. 该波的最小传播速度为 D. 该波的最大传播速度为
如图所示,一列简谐横波沿轴传播,时刻的波形图如实线所示,此时起经,第一次出现如虚线所示的波形图.已知波长为,则下列说法中正确的是( )
A. 若波向右传播,则该波的周期为
B. 若波向左传播,则该波的周期为
C. 距离波源越远的质点振动频率越小
D. 波峰位置处质点的加速度小于平衡位置处质点的加速度
、两点相距。一列简谐横波沿从到的方向传播。平衡位置在、的两个质点的振动图像分别如图中实线和虚线所示。则此列波的波长可能是
A. B. C. D.
在波的传播方向上有、两点,相距,它们的振动图象如图所示,则波的传播速度大小可能为
A. B. C. D.
简谐横波在同一均匀介质中沿轴正方向传播,波速为若某时刻在波的传播方向上,位于平衡位置的两质点、相距均为,、之间只存在一个波谷,则从该时刻起,下列四幅波形图中质点最早到达波谷的是( )
A. B.
C. D.
如图甲为一列简谐横波在某一时刻的波形图,图乙为介质中处的质点以此时刻为计时起点的振动图像.下列说法正确的是( )
A. 这列波沿轴负方向传播
B. 这列波的传播速度是
C. 经过,质点的运动方向沿轴负方向
D. 经过,质点距平衡位置的距离大于质点距平衡位置的距离
、是简谐横波传播方向上的两个质点,它们的平衡位置间的距离为。此波波速为,振幅为,周期为。在时刻,点位于平衡位置上方最大位移处。则点( )
A. 在时的加速度最大 B. 在时的速度最大
C. 在时的位移为 D. 在时的位移为
如图所示,甲图为时某向左传播的横波的波形图像,乙图为该波传播方向上某一质点的振动图像,距该质点处质点的振动图像可能是( )
A. B.
C. D.
如图所示,一列简谐横波沿轴传播,实线和虚线分别为时刻和时刻的波形图,其中,、分别是平衡位置为和的两质点。图为质点的振动图像,下列说法正确的是( )
A. B. 时刻的速度达到最大
C. 简谐横波沿轴传播的速度大小为 D. 到内,、运动的路程相等
如图甲所示,一列简谐横波沿轴传播,,为平衡位置相距的两个质点,它们的振动图像如图乙所示,则该波的波速可能是
A. B. C. D.
二、计算题(本大题共3小题,共40.0分)
一列横波在轴上传播着,在和时的波形曲线如图所示。
设周期大于,波速多大?
设周期小于,并且波速为,求波的传播方向.
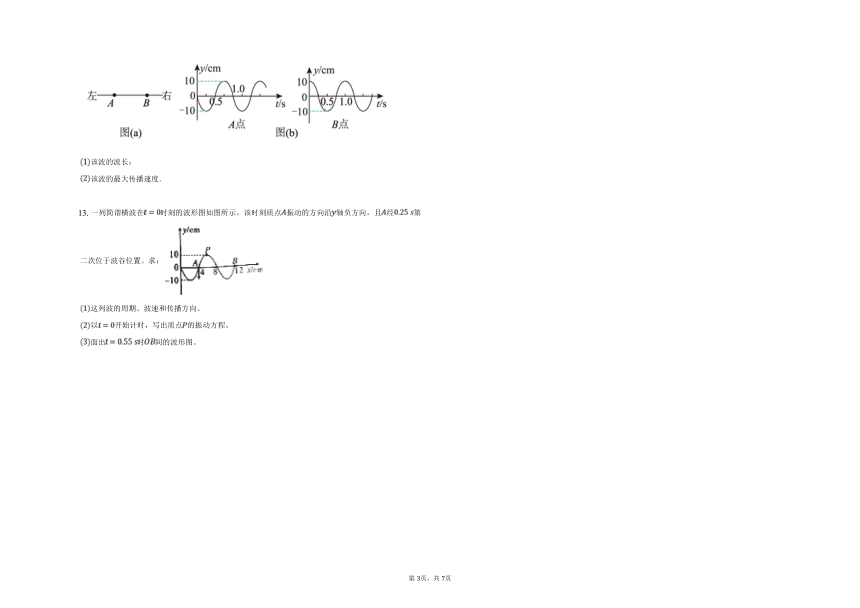
如图所示,一简谐横波沿、两点的连线传播,、两点相距,点和点的振动图像如图所示,求:
该波的波长;
该波的最大传播速度.
一列简谐横波在时刻的波形图如图所示。该时刻质点振动的方向沿轴负方向,且经第二次位于波谷位置。求:
这列波的周期、波速和传播方向。
以开始计时,写出质点的振动方程。
面出时间的波形图。
答案和解析
1.【答案】
【解析】
【分析】
不知质点的振动情况,只根据时刻与时刻在轴上的区间内的波形相同不能判断波的传播方向;根据波的传播周期性与重复性确定周期的表达式,根据波速公式确定波速。
此题要理解波的传播周期性与重复性,明确时间与周期的关系,掌握波速、频率与波长的关系。
【解答】
A.由图不能判断波的传播方向,故A错误;
由题意可知,在与两时刻在轴上至区间内的波形图相同,则有,得:所以当时,周期最大,为,波长,根据,知当时,波速最小为,故BD错误,C正确;
故选:。
2.【答案】
【解析】略
3.【答案】
【解析】
【分析】
根据根据平衡位置在、的两个质点的振动图像可知:当在波峰时,在平衡位置向下振动,画出、间最简波形图,得出此列波的波长的通式,即可解答。
本题主要考查振动图像、波的图像、机械波的多解问题。
【解答】
一列简谐横波沿从到的方向传播,根据平衡位置在、的两个质点的振动图像可知:当在波峰时,在平衡位置向下振动,画出、间最简波形图如图所示:
根据波传播的周期性可得:,,
解得此列波的波长为:,,
当时,,其它选项对应的值都不是正整数,故C正确,ABD错误。
故选C。
4.【答案】
【解析】
【分析】
此题查考机械波的图像及其多解问题,难度较易。关键要掌握由图像获得的信息。
【解析】
由振动图象可看出,,时,均处于原点,时,处于波峰,处于波谷,可知、间隔距离为半波长的奇数倍,,,,,由得,将,,代入得选项正确,选项错误。
故选B。
5.【答案】
【解析】
【分析】
根据波的传播方向判断出点的振动方向,读出波长,求出周期.分别得到质点从图示位置到达波谷的时间,从而进行比较.
解决本题的关键要确定波长与的关系,求得周期.能熟练根据波的传播方向判断质点的振动方向.
【解答】
解:图中,波长为,周期为点正向上振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向下振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向上振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向下振动,质点从图示位置到达波谷的时间;
故D图中质点最早到达波谷,故D正确,ABC错误。
故选D。
6.【答案】
【解析】A.由乙图读出,时刻质点的速度向下,则由波形的平移法可知,这列波沿轴正方向传播.故A错误; 由图知:,,则波速故B错误; 图示时刻点沿轴正方向运动,,质点的运动方向沿轴负方向,故C正确; .,经过时,质点到达波峰,而质点位于平衡位置与波谷之间,故质点距平衡位置的距离不等于质点距平衡位置的距离,故D错误; 故选:.
点睛:由振动图象读出时刻点的振动方向,判断波的传播方向.由波动图象读出波长,由振动图象读出周期,可求出波速.分析波动过程,根据时间与周期的关系,判断点的运动方向.
7.【答案】
【解析】由波速和周期可得:波长,故质点、平衡位置间的距离;那么,质点和质点正好相反;所以,在时刻,点位于平衡位置上方最大位移处波峰,质点则位于平衡位置下方最大位移处波谷;故经过后,在时,质点在平衡位置,且向轴负方向振动;质点在平衡位置,则速度最大,加速度为零,位移为零;在时,点在平衡位置,位移为零;故B正确,ACD错误;故选B。
点睛:机械振动问题中,一般根据振动图或质点振动得到周期、质点振动方向;再根据波形图得到波长和波的传播方向,从而得到波速及质点振动,进而根据周期得到路程。
8.【答案】
【解析】从题图甲可以得到波长为,从题图乙可以得到周期为,即波速为;由题图乙的振动图像可以找到时,该质点位移为负,并且向下运动,再经过就到达波谷,在题图甲中,大致标出这个质点,距该质点处的质点有左右两个点,若是该点左侧的点,在时位移为正方向且向下运动,对应选项中振动图像时刻,只有选项正确;若是该点右侧的点,在时位移为负方向且向上运动,对应选项中振动图像时刻,没有选项正确。
9.【答案】
【解析】
【分析】
本题考查识别、理解振动图像和波动图像的能力,以及把握两种图像联系的能力。
振源的振动图像反映同一质点在不同时刻的位置;波动图像反映不同质点在相同时刻的位置。要分清波的传播和质点的振动。对于波的图像往往先判断质点的振动方向和波的传播方向间的关系。同时,能熟练分析波动形成的过程,分析物理量的变化情况.
【解答】
A.因为没有说明时刻是哪个时刻,假设,根据图可知,质点在时刻正在沿轴正方向振动,则波向轴正方向传播,可得、、、,假设,根据图可知,质点在时刻正在沿轴负方向振动,则波向轴负方向传播,同理可得、、、,故A错误
B.由分析可知,无论是哪种情况,时刻质点都在波峰,振动速度等于零,最小,故 B错误
C.由图可看出波长为,周期为,则波速为,故C正确
D.到内,运动的路程可能是、、或、、,
如果,在第一个时间内,沿轴负方向运动到与轴对称的位置,路程大于振幅,则到内的路程,
同理如果,在第一个时间内,沿轴正方向运动到波峰,又沿轴负方向回到原位置,路程小于振幅,则到内的路程,可知、运动的路程不相等,故 D错误。
故选C。
10.【答案】
【解析】
【分析】
该题不是普通的横波图象题,题设给出了横波中两个质点的振动图象,因不知两质点的滞后关系因此可能会存在多解性答案,根据题设条件给出的两质点的距离关系,结合波的周期性列出周期性方程即可得出波速的表达式,进而再判断选项正确与否。
【解答】
由质点振动图像可知,周期,若波从质点传到质点,则传播时间为:
则该波的波速为:,
当时,,
当时,,
当时,,
若波从质点传到质点,则传播时间为:
则该波的波速为:,
当时,,
当时,,
当时,,
故B正确,ACD错误。
11.【答案】解:当波传播时间小于周期时,波沿传播方向前进的距离小于一个波长,当波传播的时间大于周期时,波沿传播方向前进的距离大于波长,这时从波形的变化上看出的传播距离加上个波长才是波实际传播的距离。
由图知,波长
因,所以波传播的距离可以直接由图读出,若波向右传播,则在 内传播了 ,故波速为 ;
若波向左传播,则在 内传播了 ,故速度为 。
因,所以波传播的距离大于一个波长,在 内传播的距离为 ,
因,即,因此,可得波的传播方向沿轴的负方向。
答:周期大于,波右传时,速度为 ;左传时,波速为 ;
波的传播方向向左轴负方向。
【解析】本题关键要抓住波的周期性,根据波形的平移法确定波传播距离与波长的关系,求解波速。
由图读出波长,根据波形的平移法,结合波的周期性,得出波传播的距离与波长的关系,求出波长的通项,再求解波速通项。
当波速为时,求出时间内波的传播距离,根据波形的平移法确定波传播方向。
12.【答案】解:由两质点的振动图像可知,在时刻质点在平衡位置向下振动,质点在波峰位置;
若波沿传播,则
、、、
解得:、、、
若波沿传播,则
、、、
解得:、、、
周期为,则
若波沿传播,波速
、、、
当时,
若波沿传播,波速
、、、
当时
则波速的最大值。
答:若波沿传播,则、、、若波沿传播,则、、、;
该波的最大传播速度为。
【解析】假设波的传播方向,根据两点之间的距离和波长的关系得出波长的大小;
根据公式计算出波速的大小,从而得到波速的最大值。
本题主要考查了简谐横波的相关应用,解题的关键点是熟悉公式的推导,同时要注意对波的传播情况进行分类讨论。
13.【答案】【小题】时刻质点振动的方向沿轴负方向,可知波沿轴正向传播;因点经第二次位于波谷位置,可知,解得;;
【小题】因,,则以开始计时,写出质点的振动方程为:
【小题】
,则此时原点处的质点在最低点,此时间的波形图:
【解析】 略
略
略
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
如图所示,一列简谐横波沿轴传播,时刻与时刻在轴上的区间内的波形相同.下列说法正确的是( )
A. 该波一定沿轴正方向传播 B. 该波的周期一定为
C. 该波的最小传播速度为 D. 该波的最大传播速度为
如图所示,一列简谐横波沿轴传播,时刻的波形图如实线所示,此时起经,第一次出现如虚线所示的波形图.已知波长为,则下列说法中正确的是( )
A. 若波向右传播,则该波的周期为
B. 若波向左传播,则该波的周期为
C. 距离波源越远的质点振动频率越小
D. 波峰位置处质点的加速度小于平衡位置处质点的加速度
、两点相距。一列简谐横波沿从到的方向传播。平衡位置在、的两个质点的振动图像分别如图中实线和虚线所示。则此列波的波长可能是
A. B. C. D.
在波的传播方向上有、两点,相距,它们的振动图象如图所示,则波的传播速度大小可能为
A. B. C. D.
简谐横波在同一均匀介质中沿轴正方向传播,波速为若某时刻在波的传播方向上,位于平衡位置的两质点、相距均为,、之间只存在一个波谷,则从该时刻起,下列四幅波形图中质点最早到达波谷的是( )
A. B.
C. D.
如图甲为一列简谐横波在某一时刻的波形图,图乙为介质中处的质点以此时刻为计时起点的振动图像.下列说法正确的是( )
A. 这列波沿轴负方向传播
B. 这列波的传播速度是
C. 经过,质点的运动方向沿轴负方向
D. 经过,质点距平衡位置的距离大于质点距平衡位置的距离
、是简谐横波传播方向上的两个质点,它们的平衡位置间的距离为。此波波速为,振幅为,周期为。在时刻,点位于平衡位置上方最大位移处。则点( )
A. 在时的加速度最大 B. 在时的速度最大
C. 在时的位移为 D. 在时的位移为
如图所示,甲图为时某向左传播的横波的波形图像,乙图为该波传播方向上某一质点的振动图像,距该质点处质点的振动图像可能是( )
A. B.
C. D.
如图所示,一列简谐横波沿轴传播,实线和虚线分别为时刻和时刻的波形图,其中,、分别是平衡位置为和的两质点。图为质点的振动图像,下列说法正确的是( )
A. B. 时刻的速度达到最大
C. 简谐横波沿轴传播的速度大小为 D. 到内,、运动的路程相等
如图甲所示,一列简谐横波沿轴传播,,为平衡位置相距的两个质点,它们的振动图像如图乙所示,则该波的波速可能是
A. B. C. D.
二、计算题(本大题共3小题,共40.0分)
一列横波在轴上传播着,在和时的波形曲线如图所示。
设周期大于,波速多大?
设周期小于,并且波速为,求波的传播方向.
如图所示,一简谐横波沿、两点的连线传播,、两点相距,点和点的振动图像如图所示,求:
该波的波长;
该波的最大传播速度.
一列简谐横波在时刻的波形图如图所示。该时刻质点振动的方向沿轴负方向,且经第二次位于波谷位置。求:
这列波的周期、波速和传播方向。
以开始计时,写出质点的振动方程。
面出时间的波形图。
答案和解析
1.【答案】
【解析】
【分析】
不知质点的振动情况,只根据时刻与时刻在轴上的区间内的波形相同不能判断波的传播方向;根据波的传播周期性与重复性确定周期的表达式,根据波速公式确定波速。
此题要理解波的传播周期性与重复性,明确时间与周期的关系,掌握波速、频率与波长的关系。
【解答】
A.由图不能判断波的传播方向,故A错误;
由题意可知,在与两时刻在轴上至区间内的波形图相同,则有,得:所以当时,周期最大,为,波长,根据,知当时,波速最小为,故BD错误,C正确;
故选:。
2.【答案】
【解析】略
3.【答案】
【解析】
【分析】
根据根据平衡位置在、的两个质点的振动图像可知:当在波峰时,在平衡位置向下振动,画出、间最简波形图,得出此列波的波长的通式,即可解答。
本题主要考查振动图像、波的图像、机械波的多解问题。
【解答】
一列简谐横波沿从到的方向传播,根据平衡位置在、的两个质点的振动图像可知:当在波峰时,在平衡位置向下振动,画出、间最简波形图如图所示:
根据波传播的周期性可得:,,
解得此列波的波长为:,,
当时,,其它选项对应的值都不是正整数,故C正确,ABD错误。
故选C。
4.【答案】
【解析】
【分析】
此题查考机械波的图像及其多解问题,难度较易。关键要掌握由图像获得的信息。
【解析】
由振动图象可看出,,时,均处于原点,时,处于波峰,处于波谷,可知、间隔距离为半波长的奇数倍,,,,,由得,将,,代入得选项正确,选项错误。
故选B。
5.【答案】
【解析】
【分析】
根据波的传播方向判断出点的振动方向,读出波长,求出周期.分别得到质点从图示位置到达波谷的时间,从而进行比较.
解决本题的关键要确定波长与的关系,求得周期.能熟练根据波的传播方向判断质点的振动方向.
【解答】
解:图中,波长为,周期为点正向上振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向下振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向上振动,质点从图示位置到达波谷的时间;
图中,波长为,周期为点正向下振动,质点从图示位置到达波谷的时间;
故D图中质点最早到达波谷,故D正确,ABC错误。
故选D。
6.【答案】
【解析】A.由乙图读出,时刻质点的速度向下,则由波形的平移法可知,这列波沿轴正方向传播.故A错误; 由图知:,,则波速故B错误; 图示时刻点沿轴正方向运动,,质点的运动方向沿轴负方向,故C正确; .,经过时,质点到达波峰,而质点位于平衡位置与波谷之间,故质点距平衡位置的距离不等于质点距平衡位置的距离,故D错误; 故选:.
点睛:由振动图象读出时刻点的振动方向,判断波的传播方向.由波动图象读出波长,由振动图象读出周期,可求出波速.分析波动过程,根据时间与周期的关系,判断点的运动方向.
7.【答案】
【解析】由波速和周期可得:波长,故质点、平衡位置间的距离;那么,质点和质点正好相反;所以,在时刻,点位于平衡位置上方最大位移处波峰,质点则位于平衡位置下方最大位移处波谷;故经过后,在时,质点在平衡位置,且向轴负方向振动;质点在平衡位置,则速度最大,加速度为零,位移为零;在时,点在平衡位置,位移为零;故B正确,ACD错误;故选B。
点睛:机械振动问题中,一般根据振动图或质点振动得到周期、质点振动方向;再根据波形图得到波长和波的传播方向,从而得到波速及质点振动,进而根据周期得到路程。
8.【答案】
【解析】从题图甲可以得到波长为,从题图乙可以得到周期为,即波速为;由题图乙的振动图像可以找到时,该质点位移为负,并且向下运动,再经过就到达波谷,在题图甲中,大致标出这个质点,距该质点处的质点有左右两个点,若是该点左侧的点,在时位移为正方向且向下运动,对应选项中振动图像时刻,只有选项正确;若是该点右侧的点,在时位移为负方向且向上运动,对应选项中振动图像时刻,没有选项正确。
9.【答案】
【解析】
【分析】
本题考查识别、理解振动图像和波动图像的能力,以及把握两种图像联系的能力。
振源的振动图像反映同一质点在不同时刻的位置;波动图像反映不同质点在相同时刻的位置。要分清波的传播和质点的振动。对于波的图像往往先判断质点的振动方向和波的传播方向间的关系。同时,能熟练分析波动形成的过程,分析物理量的变化情况.
【解答】
A.因为没有说明时刻是哪个时刻,假设,根据图可知,质点在时刻正在沿轴正方向振动,则波向轴正方向传播,可得、、、,假设,根据图可知,质点在时刻正在沿轴负方向振动,则波向轴负方向传播,同理可得、、、,故A错误
B.由分析可知,无论是哪种情况,时刻质点都在波峰,振动速度等于零,最小,故 B错误
C.由图可看出波长为,周期为,则波速为,故C正确
D.到内,运动的路程可能是、、或、、,
如果,在第一个时间内,沿轴负方向运动到与轴对称的位置,路程大于振幅,则到内的路程,
同理如果,在第一个时间内,沿轴正方向运动到波峰,又沿轴负方向回到原位置,路程小于振幅,则到内的路程,可知、运动的路程不相等,故 D错误。
故选C。
10.【答案】
【解析】
【分析】
该题不是普通的横波图象题,题设给出了横波中两个质点的振动图象,因不知两质点的滞后关系因此可能会存在多解性答案,根据题设条件给出的两质点的距离关系,结合波的周期性列出周期性方程即可得出波速的表达式,进而再判断选项正确与否。
【解答】
由质点振动图像可知,周期,若波从质点传到质点,则传播时间为:
则该波的波速为:,
当时,,
当时,,
当时,,
若波从质点传到质点,则传播时间为:
则该波的波速为:,
当时,,
当时,,
当时,,
故B正确,ACD错误。
11.【答案】解:当波传播时间小于周期时,波沿传播方向前进的距离小于一个波长,当波传播的时间大于周期时,波沿传播方向前进的距离大于波长,这时从波形的变化上看出的传播距离加上个波长才是波实际传播的距离。
由图知,波长
因,所以波传播的距离可以直接由图读出,若波向右传播,则在 内传播了 ,故波速为 ;
若波向左传播,则在 内传播了 ,故速度为 。
因,所以波传播的距离大于一个波长,在 内传播的距离为 ,
因,即,因此,可得波的传播方向沿轴的负方向。
答:周期大于,波右传时,速度为 ;左传时,波速为 ;
波的传播方向向左轴负方向。
【解析】本题关键要抓住波的周期性,根据波形的平移法确定波传播距离与波长的关系,求解波速。
由图读出波长,根据波形的平移法,结合波的周期性,得出波传播的距离与波长的关系,求出波长的通项,再求解波速通项。
当波速为时,求出时间内波的传播距离,根据波形的平移法确定波传播方向。
12.【答案】解:由两质点的振动图像可知,在时刻质点在平衡位置向下振动,质点在波峰位置;
若波沿传播,则
、、、
解得:、、、
若波沿传播,则
、、、
解得:、、、
周期为,则
若波沿传播,波速
、、、
当时,
若波沿传播,波速
、、、
当时
则波速的最大值。
答:若波沿传播,则、、、若波沿传播,则、、、;
该波的最大传播速度为。
【解析】假设波的传播方向,根据两点之间的距离和波长的关系得出波长的大小;
根据公式计算出波速的大小,从而得到波速的最大值。
本题主要考查了简谐横波的相关应用,解题的关键点是熟悉公式的推导,同时要注意对波的传播情况进行分类讨论。
13.【答案】【小题】时刻质点振动的方向沿轴负方向,可知波沿轴正向传播;因点经第二次位于波谷位置,可知,解得;;
【小题】因,,则以开始计时,写出质点的振动方程为:
【小题】
,则此时原点处的质点在最低点,此时间的波形图:
【解析】 略
略
略
第1页,共1页
