北师大版八年级数学上册7.1为什么要证明 课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上册7.1为什么要证明 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 852.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 19:10:22 | ||
图片预览







文档简介
(共21张PPT)
八年级上册
7.1 为什么要证明
理解通过观察、猜测得到的结论不一定正确.
01
02
本节目标
了解要判定一个数学结论正确与否,需要进行有根有据的推理.
03
初步感受数学中证明的必要性,发展推理意识.
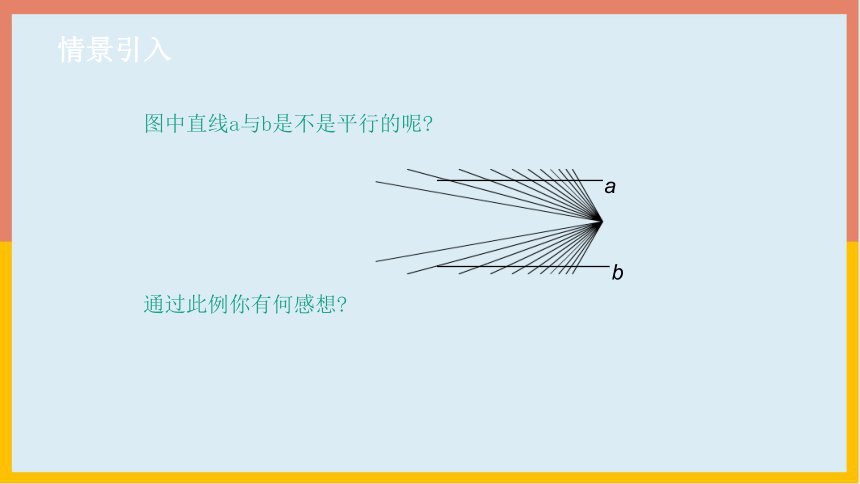
图中直线a与b是不是平行的呢
通过此例你有何感想
情景引入
a
b
图中直线a与b是不是平行的呢
通过此例你有何感想
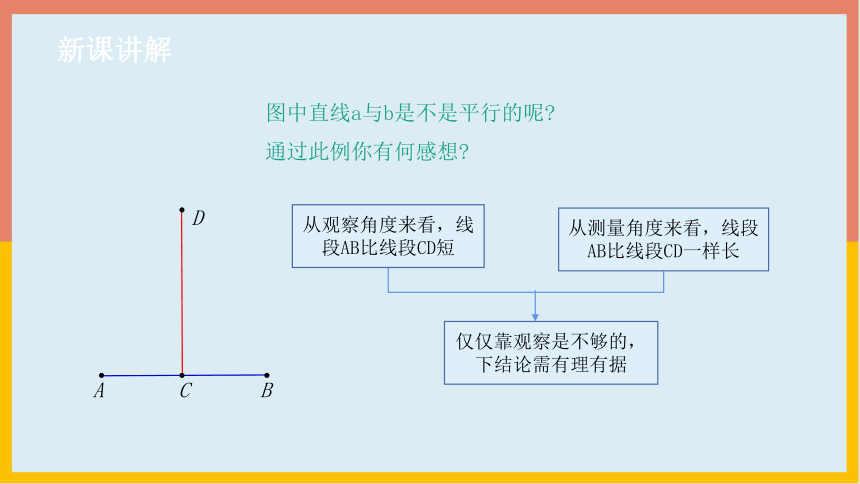
A
B
C
D
从观察角度来看,线段AB比线段CD短
从测量角度来看,线段AB比线段CD一样长
仅仅靠观察是不够的,下结论需有理有据
新课讲解
新课讲解
注意:
(1)直觉有时会产生错误,不是永远可信的.
(2)图形的性质并不都是通过测量得出的.
(3)对少数具体例子的观察、测量或计算得出的结论.并不能保证一般情况下都成立.
(4)只有通过推理的方法研究问题,才能揭示问题的本质.
新课讲解
2.检验数学结论常用的方法
主要有:实验验证、举出反例、推理论证.
实验验证法:通过实验、测量、计算等手段验证结论正确与否;实验验证是最基本的方法,它直接反映由具体到抽象、由特殊到一般的逻辑思维方法.
举出反例:举出一个例子,说明结论是错误的,举出反例常用于说明该数学结论不一定成立.
推理论证:任何推理都包含两个部分,前提是推理的依据部分,可以一个。也可以多个,结论是前提推出的判断.在“前提”下,严格推理论证“结论”正确是否可靠. 推理论证是最可靠、最科学的方法.是我们要掌握的重点.实际上每一个正确的结论都需要我们进行严格的推理证明才能得出.
检验数学结论的具体过程:观察、度量、实验→猜想归纳→结论→推理正确结论.
新课讲解
(1)说明一个结论错误,只需举出一个反例即可,反例的选取一定要满足所给题设的要求,而不能满足原结论.
(2)要证明一个结论正确,仅靠举例说明是不够的,需要进行推理证明.
(3)推理是从一个或几个已知的判断,得出另一个判断的思维方式.
1.证明的必要性
例1 一个两位数,它的十位数字为a,个位数字为b,若把它的十位数字与个位数字对调,将得到一个新的两位数,这两个数的和能被11整除吗 我们可验证一下:比如23,把它的十位数字与个位数字对调后得到新的两位数32,而23 + 32 =55,因此我们断定,这两个数的和能被11整除问:上述说法正确吗
解:上述验证过程只是一个特例,为了验证结论的正确性,可作如下推理:
原两位数为10a +b,得到的新两位数为10b +a,
(10a+b) +(10b+a) =11(a +b),
∵11(a +b)是11的整数倍,
∴这两个数的和能被11整除.
例题精讲
方法总结
观察、归纳以及对少数具体例子的计算得出的结论不一定都正确,只有通过推理论证的方法研究问题,才能揭示问题的本质.
变式训练
如图,甲、乙两只小虫从A点同时出发,甲虫沿着大的半圆爬行,乙虫沿着内部的3个半圆爬行,如果两只虫爬行的速度相同,则先到达B点的虫子是( )
A.甲 B.同时到达 C.乙 D.不能确定
B
例题精讲
2. 证明的方法
例2观察下列等式;;…
根据以上规律,写出第n个等式,并证明第n个等式成立.
解:第n个等式为.
证明:左边=
=
=
=
=.
∴左边=右边
即.
方法总结
证明常用的三种方法:实验验证、举出反例、推理证明.实验验证法常用于检验一些比较直观、简单的结论,举出反例法多用于验证某结论不是正确的,推理证明主要用来进行严格的推理论证.
如图所示,一根细长的绳子,对折5次,用剪刀沿5次对折后的中间将绳子全部剪断,此时细绳被剪成______段.
解析:对折零次后,沿中间将绳子剪断,细绳被剪成2段;
对折一次后,沿中间将绳子剪断,细绳被剪成2+1=3段;
对折两次后,沿中间将绳子剪断,细绳被剪成2 +1=5段;
对折三次后,沿中间将绳子剪断,细绳被剪成2 +1=9段;
从而可得对折n次后,沿中间将绳子剪断,细绳被剪成2 +1段;
故对折五次后,沿中间将绳子剪断,细绳被剪成25+1=33段.
变式训练
33
设a =3 -1 ,a =5 -3 ,a =7 -5 .....容易知道a =8,a =16,a =24,如果一个数能表示为8的倍数,我们就说它能被8整除,所以a 、a 、a 都能被8整除.
(1)试证明an是否能被8整除;
(2)若一个数是一个自然数的平方,则称这个数是“幸运数”,试找出a 、a 、…an这一系列数中从小到大排列的前4个“幸运数”,并探索当n满足什么条件时,an为“幸运数”.
解:(1)由规律可知:an =(2n+1) -(2n-1) ,
则an =(2n+1) -(2n-1)
=(2n+1+2n-1)(2n+1-2n+1)= 8n;
∴an是能被8整除;
深入探究
设a =3 -1 ,a =5 -3 ,a =7 -5 .....容易知道a =8,a =16,a =24,如果一个数能表示为8的倍数,我们就说它能被8整除,所以a 、a 、a 都能被8整除.
(1)试证明an是否能被8整除;
(2)若一个数是一个自然数的平方,则称这个数是“幸运数”,试找出a 、a 、…an这一系列数中从小到大排列的前4个“幸运数”,并探索当n满足什么条件时,an为“幸运数”.
解: (2)前四个:
a =2×8=16=4 ,a8 =8×8=8 ,a18=8×18=12 ,a32=32×8=16 ,
n= 2m (m为正整数),an为“幸运数”
深入探究
1.如右图,点O在直线AB上,若∠l=40°,则∠2的度数是( )
A.50° B.60° C.140° D.150°
2.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.三角形两边之和大于第三边,
课堂练习
C
C
3. 法常用于检验一些比较直观、简单的结论; 法多用于验证某结论不正确; 主要用来进行严格的推理论证,既可以验证某结论是正确的,也可以验证某结论是不正确的.
4. 下列图案均由边长为单位长度的小正方形按一定的规律拼接而成.依此规律,第5个图案中小正方形的个数为 .
课堂练习
实验验证
41
举出反例
推理证明
5. 我们知道:2×2=4,2+2=4.试问:对于任意数a与b,是否一定有结论a×b=a+ b
解:3×2=6,而3+2=5,因为6≠5,
所以不是任意数a与b,都有结论a×b=a+b.
课堂练习
6. 如图,在□ABCD中,DF.上AC于点F,BE⊥AC于点E,试问:DF与BE的位置关系和数量关系如何 你能肯定吗 请说明理由.
解:观察得:DF // BE,
DF= BE.
理由:由DF⊥AC,BE.⊥AC,
可知∠DFC=∠BEA=90°,
故DF// BE.
由∵AB//CD,得∠DCF=∠BAE.
又AB=CD,∠CFD=∠AEB=90°,
所以△DCF≌△BAE.所以DF= BE.
课堂练习
本节总结
为什么要证明
推理的意义:数学结论必须经过严格的论证
验证数学结论的常用方法
实验验证
举出反例
推理证明
再见
八年级上册
7.1 为什么要证明
理解通过观察、猜测得到的结论不一定正确.
01
02
本节目标
了解要判定一个数学结论正确与否,需要进行有根有据的推理.
03
初步感受数学中证明的必要性,发展推理意识.
图中直线a与b是不是平行的呢
通过此例你有何感想
情景引入
a
b
图中直线a与b是不是平行的呢
通过此例你有何感想
A
B
C
D
从观察角度来看,线段AB比线段CD短
从测量角度来看,线段AB比线段CD一样长
仅仅靠观察是不够的,下结论需有理有据
新课讲解
新课讲解
注意:
(1)直觉有时会产生错误,不是永远可信的.
(2)图形的性质并不都是通过测量得出的.
(3)对少数具体例子的观察、测量或计算得出的结论.并不能保证一般情况下都成立.
(4)只有通过推理的方法研究问题,才能揭示问题的本质.
新课讲解
2.检验数学结论常用的方法
主要有:实验验证、举出反例、推理论证.
实验验证法:通过实验、测量、计算等手段验证结论正确与否;实验验证是最基本的方法,它直接反映由具体到抽象、由特殊到一般的逻辑思维方法.
举出反例:举出一个例子,说明结论是错误的,举出反例常用于说明该数学结论不一定成立.
推理论证:任何推理都包含两个部分,前提是推理的依据部分,可以一个。也可以多个,结论是前提推出的判断.在“前提”下,严格推理论证“结论”正确是否可靠. 推理论证是最可靠、最科学的方法.是我们要掌握的重点.实际上每一个正确的结论都需要我们进行严格的推理证明才能得出.
检验数学结论的具体过程:观察、度量、实验→猜想归纳→结论→推理正确结论.
新课讲解
(1)说明一个结论错误,只需举出一个反例即可,反例的选取一定要满足所给题设的要求,而不能满足原结论.
(2)要证明一个结论正确,仅靠举例说明是不够的,需要进行推理证明.
(3)推理是从一个或几个已知的判断,得出另一个判断的思维方式.
1.证明的必要性
例1 一个两位数,它的十位数字为a,个位数字为b,若把它的十位数字与个位数字对调,将得到一个新的两位数,这两个数的和能被11整除吗 我们可验证一下:比如23,把它的十位数字与个位数字对调后得到新的两位数32,而23 + 32 =55,因此我们断定,这两个数的和能被11整除问:上述说法正确吗
解:上述验证过程只是一个特例,为了验证结论的正确性,可作如下推理:
原两位数为10a +b,得到的新两位数为10b +a,
(10a+b) +(10b+a) =11(a +b),
∵11(a +b)是11的整数倍,
∴这两个数的和能被11整除.
例题精讲
方法总结
观察、归纳以及对少数具体例子的计算得出的结论不一定都正确,只有通过推理论证的方法研究问题,才能揭示问题的本质.
变式训练
如图,甲、乙两只小虫从A点同时出发,甲虫沿着大的半圆爬行,乙虫沿着内部的3个半圆爬行,如果两只虫爬行的速度相同,则先到达B点的虫子是( )
A.甲 B.同时到达 C.乙 D.不能确定
B
例题精讲
2. 证明的方法
例2观察下列等式;;…
根据以上规律,写出第n个等式,并证明第n个等式成立.
解:第n个等式为.
证明:左边=
=
=
=
=.
∴左边=右边
即.
方法总结
证明常用的三种方法:实验验证、举出反例、推理证明.实验验证法常用于检验一些比较直观、简单的结论,举出反例法多用于验证某结论不是正确的,推理证明主要用来进行严格的推理论证.
如图所示,一根细长的绳子,对折5次,用剪刀沿5次对折后的中间将绳子全部剪断,此时细绳被剪成______段.
解析:对折零次后,沿中间将绳子剪断,细绳被剪成2段;
对折一次后,沿中间将绳子剪断,细绳被剪成2+1=3段;
对折两次后,沿中间将绳子剪断,细绳被剪成2 +1=5段;
对折三次后,沿中间将绳子剪断,细绳被剪成2 +1=9段;
从而可得对折n次后,沿中间将绳子剪断,细绳被剪成2 +1段;
故对折五次后,沿中间将绳子剪断,细绳被剪成25+1=33段.
变式训练
33
设a =3 -1 ,a =5 -3 ,a =7 -5 .....容易知道a =8,a =16,a =24,如果一个数能表示为8的倍数,我们就说它能被8整除,所以a 、a 、a 都能被8整除.
(1)试证明an是否能被8整除;
(2)若一个数是一个自然数的平方,则称这个数是“幸运数”,试找出a 、a 、…an这一系列数中从小到大排列的前4个“幸运数”,并探索当n满足什么条件时,an为“幸运数”.
解:(1)由规律可知:an =(2n+1) -(2n-1) ,
则an =(2n+1) -(2n-1)
=(2n+1+2n-1)(2n+1-2n+1)= 8n;
∴an是能被8整除;
深入探究
设a =3 -1 ,a =5 -3 ,a =7 -5 .....容易知道a =8,a =16,a =24,如果一个数能表示为8的倍数,我们就说它能被8整除,所以a 、a 、a 都能被8整除.
(1)试证明an是否能被8整除;
(2)若一个数是一个自然数的平方,则称这个数是“幸运数”,试找出a 、a 、…an这一系列数中从小到大排列的前4个“幸运数”,并探索当n满足什么条件时,an为“幸运数”.
解: (2)前四个:
a =2×8=16=4 ,a8 =8×8=8 ,a18=8×18=12 ,a32=32×8=16 ,
n= 2m (m为正整数),an为“幸运数”
深入探究
1.如右图,点O在直线AB上,若∠l=40°,则∠2的度数是( )
A.50° B.60° C.140° D.150°
2.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.三角形两边之和大于第三边,
课堂练习
C
C
3. 法常用于检验一些比较直观、简单的结论; 法多用于验证某结论不正确; 主要用来进行严格的推理论证,既可以验证某结论是正确的,也可以验证某结论是不正确的.
4. 下列图案均由边长为单位长度的小正方形按一定的规律拼接而成.依此规律,第5个图案中小正方形的个数为 .
课堂练习
实验验证
41
举出反例
推理证明
5. 我们知道:2×2=4,2+2=4.试问:对于任意数a与b,是否一定有结论a×b=a+ b
解:3×2=6,而3+2=5,因为6≠5,
所以不是任意数a与b,都有结论a×b=a+b.
课堂练习
6. 如图,在□ABCD中,DF.上AC于点F,BE⊥AC于点E,试问:DF与BE的位置关系和数量关系如何 你能肯定吗 请说明理由.
解:观察得:DF // BE,
DF= BE.
理由:由DF⊥AC,BE.⊥AC,
可知∠DFC=∠BEA=90°,
故DF// BE.
由∵AB//CD,得∠DCF=∠BAE.
又AB=CD,∠CFD=∠AEB=90°,
所以△DCF≌△BAE.所以DF= BE.
课堂练习
本节总结
为什么要证明
推理的意义:数学结论必须经过严格的论证
验证数学结论的常用方法
实验验证
举出反例
推理证明
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
