北师大版八年级数学上册第5章二元一次方程组章末复习课件(共35张PPT)
文档属性
| 名称 | 北师大版八年级数学上册第5章二元一次方程组章末复习课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
八年级上册
二元一次方程组章末复习
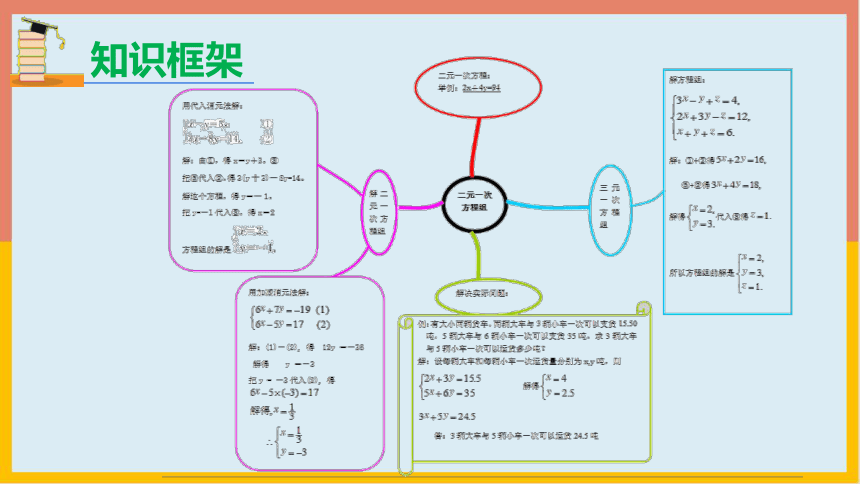
知识框架
(一)二元一次方程组及其解法
1.二元一次方程概念:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
2. 二元一次方程组概念:共含有两个未知数的两个方程所组成的方程组,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
3.二元一次方程的解:适合一个二元一次方程的一组未知数的值,叫这个二元一次方程的一组解.
注意:一个二元一次方程有无数解.
知识回顾
4. 二元一次方程组的解:
二元一次方程组中各个方程的公共解叫做二元一次方程组的解.
5.二元一次方程组的解法:代入消元法和加减消元法.
1.已知方程 是关于x,y的二元一次方程,则m= 1 ,n= 2 .
2.在(1) ,(2) ,(3) 中, ⑴ ⑶ 是方程 的解; ⑵ ⑶ 是程 的解; ⑶ 是方程组
的解.
考点对接
3.下列方程组属于二元一次方程组的是( )
4.求二元一次方程3x+2y=12的非负整数解.
解:原方程可化为
由于x、y为非负整数,所以x必为偶数.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0.
所以原方程的的非负整数解为
B
5.用代入法解方程组
解:由①得y=2x-3 ③,
把③代代入②得,3x+4(2x-3)=10,
解得:x=2,
把x=2代入③得,y=1
所以原方程的解为
6.解方程组
解:①×3-②得,2y=4,
y=2,
把y=2代入①得
则原方程的解为
7. 上数学课时,陈老师让同学们解一道关于x、y的方程组并请小方和小龙两位同学到黑板上板演.可是小方同学看错了方程①中的a,得到方程组的解为小龙同学看错了方程②中的b,得到方程组的解为你能按正确的a、 b值求出方程组的解吗?请试一试.
解:由题意得方程组
解得
代入原方程组,得
解得
(二)二元一次方程组的应用
1.列方程组解应用题:设出两个未知量,列方程组解应用题.
2.二元一次方程与一次函数:一般的,以二元一次方程的解为坐标的点组成的图像与相应的一次函数的图像相同,是一条直线.
3. 用二元一次方程组确定一次函数的表达式:
用待定系数法确定一次函数的表达式的步骤:
(1)设一次函数的表达式为y=kx+b,
(2)把函数的两组对应值代入所设函数中,得到一个关于k、b的二元一次方程组,解方程组求出k,b的值,
(3)把k、b的值代入所设的函数中,写出一次函数的表达式.
知识回顾
(二)二元一次方程组的应用
4. 三元一次方程组
三元一次方程的概念:三元一次方程就是含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1, 2a-3b+c=0等都是三元一次方程.
三元一次方程组的概念: 一般地,由几个一次方程组成,并且一共只含三个未知数的方程组,叫做三元一次方程组.
三元一次方程组的解法
解三元一次方程组的基本思想也是消元,一般地,应利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.
1. 某校课外小组的学生准备分组外出活动,若每组7人,则余下3人;若每组8人,则少5人,求课外小组的人数x和应分成的组数y.依题意得( )
A. B.
C. D.
C
考点对接
2. 为了改善住房条件,小亮父母考察了某小区的 A,B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房比A套楼房的面积大24平方米,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A套楼房的面积为x平方米,B套楼房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
A. B. C. D.
D
3. 一个两位数,数字之和为11,若原数加45,等于此两位数交换其数位上的数的位置后得到的新数,求原数是多少?若设原数十位数字为x,个位数字为y,根据题意列出的下列方程组中正确的是( )
A. B.
C. D.以上都不对
C
4.一条船在一条河上的顺流航行速度是逆流航行速度的3倍,这条船在静水中的航速与河水的流速之比是( )
A.3∶1 B.2∶1
C.1∶1 D.5∶2
5. 一次函数y=kx+b的图象与x 轴、y轴的交点坐标分别是(2,0)、(0,-1),这个一次函数的表达式为( )
A.y=x-1 B.y=2x+2
C.y=-x-1 D.y=2x-1
B
A
6.弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
A.9 cm
B.10 cm
C.10.5 cm
D.11 cm
B
7.甲、乙两人以相同路线前往距离单位10 km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程s(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
B
8. 甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50﹪的利润定价,乙服装按40﹪的利润定价。在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
解:设甲服装的成本是x元,乙服装的成本是y元,
依题意得,
解得
答:甲、乙两件服装的成本分别为300元、200元
9. 百货大楼购进某种商品后,加价40%作为销售价,商场搞优惠促销活动,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款399元,这两种商品原销售价之和为490元.
(1)这两种商品的进价分别为多少元?(保留到个位)
(2)对这两种商品而言,商场是赔了,还是赚了?赔、赚了多少钱?
(3)请你帮助商店设计一下,以这两种商品为例,折扣最低为多少方能保证商场只赚不赔?
(4)如果依然让顾客感到低折扣的实惠,那你看怎样设计商品的折扣作为奖励,既使顾客尝到低折扣的购物满足感,而又能保证商场在旺销中有钱可赚?
10.从小华家到姥姥家,有一段上坡路和一段下坡路.星期天,小华骑自行车去姥姥家,如果保持上坡每小时行3 km,下坡每小时行5 km,他到姥姥家需要行66分钟,从姥姥家回来时需要行78分钟才能到家.那么,从小华家到姥姥家上坡路和下坡路各有多少千米,姥姥家离小华家有多远?
解:设小华到姥姥家上坡路有x km,下坡路有y km,那么小华从姥姥家回来,需要走上坡路y km,下坡路x km.根据题意得:
所以,小华到姥姥家有1.5 km上坡路,3 km下坡路,姥姥家离小华家4.5 km.
11.如图,l甲、l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:
(1)乙出发时,与甲相距________千米;
(2)走了一段路程后,乙的自行车发生故障,
停下来修理,修车的时间为______小时;
(3)乙从出发起,经过______小时与甲相遇;
(4)甲行走的路程s(千米)与时间t(时)之间的函数关系是 ;
(5)如果乙的自行车不出现故障,那么乙出发后经过______时与甲相遇,相遇处离乙的出发点______千米,并在图中标出其相遇点.
10
1
3
12.在等式y=ax2+bx+c中,当x=1时,y=0;当x=-1时,y=0;当x=0时,y=5.求a,b,c的值.
解:依题意,得:
解得
1.下列方程是二元一次方程的是( ).
A.x2+x=1 B.2x+3y-1=0
C.x+y-z=0 D.x+ +1=0
2.若 与 的和是单项式,则( ).
A. B.
C. D.
B
B
随堂检测
3.如果 是方程组 的解,则m,n的值是( ).
A. B.
C. D.
4.若方程x+y=3,x-y=5和x+ky=2有公共解,则k的值是( ).
A.3 B.-2
C.1 D.2
B
D
5.李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.已知他骑自行车的平均速度是250米/分,步行的平均速度是80米/分,他家到学校的距离是2 900米.如果设他骑车和步行的时间分别为x 分钟,y分钟,那么可列出的方程组是 ( )
A. B.
C. D.
D
6.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是18岁.”如果设现在弟弟的年龄是x 岁,哥哥的年龄是y岁,那么下列方程组正确的是 ( )
A. B.
C. D.
D
7.2016年春季我国部分地区大旱,导致农田减产,图是一对农民父子的对话内容,请根据对话内容分别求出该农户今年第一块和第二块农田的花生产量分别是( )
A.100千克和370 千克 B.370千克和100千克
C.20千克和37千克 D.37千克和20千克
C
8.已知ax=by+2 018的一个解是 求a+b的值.
解:把
代入ax =by+2 018中,
得a=-b+2 018,
所以a+b=2 018.
9.已知:4x-3y-6z=0,x+2y-7z=0,且x,y,z都不为零.求 的值.
解:解关于x、y的二元一次方程组
解得
把x=3z,y=2z代入得,原式 =
10.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需 315元;若购甲4件,乙10件,丙1件,共需420元.现在购甲、乙、丙各一件共需多少元
解:设购甲、乙、丙各一件分别需要x,y,z元,则
①×3-②×2得:x+y+z=105.
购甲、乙、丙各一件共需105元.
11.某校七年级200名学生参加期中考试,数学成绩的情况如下表,这次 考试中及格和不及格的学生人数各是多少?
平均分
及格学生 87
不及格学生 43
七年级 76
解:设这次考试中及格和不及格的学生分别有x人和y人.由题意,得
解得
答:这次考试中及格和不及格的学生分别有150人和50人.
二元一次方程组
定义
解法
代入消元法
加减消元法
应用
实际问题
课堂小结
布置作业
书面作业:完成相关书本作业
再见
八年级上册
二元一次方程组章末复习
知识框架
(一)二元一次方程组及其解法
1.二元一次方程概念:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
2. 二元一次方程组概念:共含有两个未知数的两个方程所组成的方程组,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
3.二元一次方程的解:适合一个二元一次方程的一组未知数的值,叫这个二元一次方程的一组解.
注意:一个二元一次方程有无数解.
知识回顾
4. 二元一次方程组的解:
二元一次方程组中各个方程的公共解叫做二元一次方程组的解.
5.二元一次方程组的解法:代入消元法和加减消元法.
1.已知方程 是关于x,y的二元一次方程,则m= 1 ,n= 2 .
2.在(1) ,(2) ,(3) 中, ⑴ ⑶ 是方程 的解; ⑵ ⑶ 是程 的解; ⑶ 是方程组
的解.
考点对接
3.下列方程组属于二元一次方程组的是( )
4.求二元一次方程3x+2y=12的非负整数解.
解:原方程可化为
由于x、y为非负整数,所以x必为偶数.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0.
所以原方程的的非负整数解为
B
5.用代入法解方程组
解:由①得y=2x-3 ③,
把③代代入②得,3x+4(2x-3)=10,
解得:x=2,
把x=2代入③得,y=1
所以原方程的解为
6.解方程组
解:①×3-②得,2y=4,
y=2,
把y=2代入①得
则原方程的解为
7. 上数学课时,陈老师让同学们解一道关于x、y的方程组并请小方和小龙两位同学到黑板上板演.可是小方同学看错了方程①中的a,得到方程组的解为小龙同学看错了方程②中的b,得到方程组的解为你能按正确的a、 b值求出方程组的解吗?请试一试.
解:由题意得方程组
解得
代入原方程组,得
解得
(二)二元一次方程组的应用
1.列方程组解应用题:设出两个未知量,列方程组解应用题.
2.二元一次方程与一次函数:一般的,以二元一次方程的解为坐标的点组成的图像与相应的一次函数的图像相同,是一条直线.
3. 用二元一次方程组确定一次函数的表达式:
用待定系数法确定一次函数的表达式的步骤:
(1)设一次函数的表达式为y=kx+b,
(2)把函数的两组对应值代入所设函数中,得到一个关于k、b的二元一次方程组,解方程组求出k,b的值,
(3)把k、b的值代入所设的函数中,写出一次函数的表达式.
知识回顾
(二)二元一次方程组的应用
4. 三元一次方程组
三元一次方程的概念:三元一次方程就是含有三个未知数,并且含有未知数的项的次数都是1的整式方程.如x+y-z=1, 2a-3b+c=0等都是三元一次方程.
三元一次方程组的概念: 一般地,由几个一次方程组成,并且一共只含三个未知数的方程组,叫做三元一次方程组.
三元一次方程组的解法
解三元一次方程组的基本思想也是消元,一般地,应利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.
1. 某校课外小组的学生准备分组外出活动,若每组7人,则余下3人;若每组8人,则少5人,求课外小组的人数x和应分成的组数y.依题意得( )
A. B.
C. D.
C
考点对接
2. 为了改善住房条件,小亮父母考察了某小区的 A,B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房比A套楼房的面积大24平方米,两套楼房的总房价相同,第3层楼和第5层楼每平方米的价格分别是平均价格的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设A套楼房的面积为x平方米,B套楼房的面积为y平方米,根据以上信息得出了下列方程组,其中正确的是( )
A. B. C. D.
D
3. 一个两位数,数字之和为11,若原数加45,等于此两位数交换其数位上的数的位置后得到的新数,求原数是多少?若设原数十位数字为x,个位数字为y,根据题意列出的下列方程组中正确的是( )
A. B.
C. D.以上都不对
C
4.一条船在一条河上的顺流航行速度是逆流航行速度的3倍,这条船在静水中的航速与河水的流速之比是( )
A.3∶1 B.2∶1
C.1∶1 D.5∶2
5. 一次函数y=kx+b的图象与x 轴、y轴的交点坐标分别是(2,0)、(0,-1),这个一次函数的表达式为( )
A.y=x-1 B.y=2x+2
C.y=-x-1 D.y=2x-1
B
A
6.弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如图所示,则弹簧不挂物体时的长度是( )
A.9 cm
B.10 cm
C.10.5 cm
D.11 cm
B
7.甲、乙两人以相同路线前往距离单位10 km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程s(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 km后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
B
8. 甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50﹪的利润定价,乙服装按40﹪的利润定价。在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
解:设甲服装的成本是x元,乙服装的成本是y元,
依题意得,
解得
答:甲、乙两件服装的成本分别为300元、200元
9. 百货大楼购进某种商品后,加价40%作为销售价,商场搞优惠促销活动,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款399元,这两种商品原销售价之和为490元.
(1)这两种商品的进价分别为多少元?(保留到个位)
(2)对这两种商品而言,商场是赔了,还是赚了?赔、赚了多少钱?
(3)请你帮助商店设计一下,以这两种商品为例,折扣最低为多少方能保证商场只赚不赔?
(4)如果依然让顾客感到低折扣的实惠,那你看怎样设计商品的折扣作为奖励,既使顾客尝到低折扣的购物满足感,而又能保证商场在旺销中有钱可赚?
10.从小华家到姥姥家,有一段上坡路和一段下坡路.星期天,小华骑自行车去姥姥家,如果保持上坡每小时行3 km,下坡每小时行5 km,他到姥姥家需要行66分钟,从姥姥家回来时需要行78分钟才能到家.那么,从小华家到姥姥家上坡路和下坡路各有多少千米,姥姥家离小华家有多远?
解:设小华到姥姥家上坡路有x km,下坡路有y km,那么小华从姥姥家回来,需要走上坡路y km,下坡路x km.根据题意得:
所以,小华到姥姥家有1.5 km上坡路,3 km下坡路,姥姥家离小华家4.5 km.
11.如图,l甲、l乙分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:
(1)乙出发时,与甲相距________千米;
(2)走了一段路程后,乙的自行车发生故障,
停下来修理,修车的时间为______小时;
(3)乙从出发起,经过______小时与甲相遇;
(4)甲行走的路程s(千米)与时间t(时)之间的函数关系是 ;
(5)如果乙的自行车不出现故障,那么乙出发后经过______时与甲相遇,相遇处离乙的出发点______千米,并在图中标出其相遇点.
10
1
3
12.在等式y=ax2+bx+c中,当x=1时,y=0;当x=-1时,y=0;当x=0时,y=5.求a,b,c的值.
解:依题意,得:
解得
1.下列方程是二元一次方程的是( ).
A.x2+x=1 B.2x+3y-1=0
C.x+y-z=0 D.x+ +1=0
2.若 与 的和是单项式,则( ).
A. B.
C. D.
B
B
随堂检测
3.如果 是方程组 的解,则m,n的值是( ).
A. B.
C. D.
4.若方程x+y=3,x-y=5和x+ky=2有公共解,则k的值是( ).
A.3 B.-2
C.1 D.2
B
D
5.李明同学早上骑自行车上学,中途因道路施工步行一段路,到学校共用时15分钟.已知他骑自行车的平均速度是250米/分,步行的平均速度是80米/分,他家到学校的距离是2 900米.如果设他骑车和步行的时间分别为x 分钟,y分钟,那么可列出的方程组是 ( )
A. B.
C. D.
D
6.哥哥与弟弟的年龄和是18岁,弟弟对哥哥说:“当我的年龄是你现在年龄的时候,你就是18岁.”如果设现在弟弟的年龄是x 岁,哥哥的年龄是y岁,那么下列方程组正确的是 ( )
A. B.
C. D.
D
7.2016年春季我国部分地区大旱,导致农田减产,图是一对农民父子的对话内容,请根据对话内容分别求出该农户今年第一块和第二块农田的花生产量分别是( )
A.100千克和370 千克 B.370千克和100千克
C.20千克和37千克 D.37千克和20千克
C
8.已知ax=by+2 018的一个解是 求a+b的值.
解:把
代入ax =by+2 018中,
得a=-b+2 018,
所以a+b=2 018.
9.已知:4x-3y-6z=0,x+2y-7z=0,且x,y,z都不为零.求 的值.
解:解关于x、y的二元一次方程组
解得
把x=3z,y=2z代入得,原式 =
10.有甲、乙、丙三种货物,若购甲3件,乙7件,丙1件,共需 315元;若购甲4件,乙10件,丙1件,共需420元.现在购甲、乙、丙各一件共需多少元
解:设购甲、乙、丙各一件分别需要x,y,z元,则
①×3-②×2得:x+y+z=105.
购甲、乙、丙各一件共需105元.
11.某校七年级200名学生参加期中考试,数学成绩的情况如下表,这次 考试中及格和不及格的学生人数各是多少?
平均分
及格学生 87
不及格学生 43
七年级 76
解:设这次考试中及格和不及格的学生分别有x人和y人.由题意,得
解得
答:这次考试中及格和不及格的学生分别有150人和50人.
二元一次方程组
定义
解法
代入消元法
加减消元法
应用
实际问题
课堂小结
布置作业
书面作业:完成相关书本作业
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
