人教A版(2019)高中数学选择性必修第二册 《等差数列---概念和通项公式》名师课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 《等差数列---概念和通项公式》名师课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 14:55:00 | ||
图片预览










文档简介
(共37张PPT)
1.数列的定义:
按一定次序排列的一列数
2.数列的通项公式:
数列的第项与项数之间的函数关系式,即.
复习引入
人教A版同步教材名师课件
等差数列
---概念和通项公式
学习目标
学 习 目 标 核心素养
理解等差数列的概念 数学抽象
掌握等差数列通项公式的求法 数学运算
理解等差数列与一次函数的关系 直观想象
学习目标
学习目标:
1.理解等差数列的概念.
2.掌握等差数列的通项公式及应用.
3.掌握等差数列的判定方法.
学科核心素养:
1.通过学习等差中项及等差数列通项公式的应用,体现了数学运算素养.
2.借助等差数列的判断与证明,培养学生的逻辑推理素养.
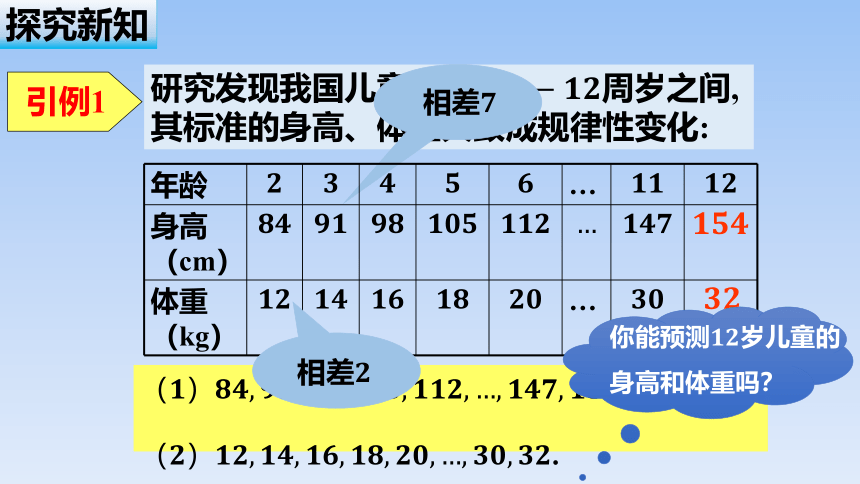
研究发现我国儿童年龄在周岁之间,其标准的身高、体重大致成规律性变化:
相差
年龄 …
身高(cm)
体重(kg) …
.
引例1
探究新知
相差
你能预测岁儿童的
身高和体重吗?
,雅典举行第一届现代奥运会,到年的北京奥运会已经是第届奥运会
你能预测出第届
奥运会的时间吗?
相差
探究新知
引例2
.
请问:它们有什么共同特点?
共同特点:从第项起,每一项与它的前一项的差等于同一个常数.
定义:如果一个数列从第项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
探究新知
即.
1.等差数列
这个常数叫做等差数列的公差,公差通常用表示.
.
2.等差中项
(1)前提:三个数成等差数列.
(2)结论:_____叫做的等差中项.
(3)满足的关系式:________.
提示:.
探究新知
【思考】等式“” 有哪些等价形式
是
不是
不是
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项和公差, 如果不是,说明理由.
(1)
(2)
(3)
(4)
(5)
(6)
说明:判断一个数列是不是等差数列,主要是由定义进行判断:
看同一个常数.
是
是
是
新知练习
当 时,
当 时,
当 时,
说明:由定义知
数列是常数列;
数列是递增数列;
数列是递减数列.
探究新知
思 考:在这个数列中?
请试着找规律填空:
探究新知
所以
由此得到:
问题:如果已知一个等差数列的首项是 ,公差是 ,那么这个数列的通项 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
探究新知
由此得到:
分析2:根据等差数列的定义:
探究新知
将上面个等式相加得:
累加法
(通项公式)
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
探究新知
2.等差数列的通项公式
,当时,是一次函数,当时的函数.
等差数列的图象是点组成的集合,这些点均匀分布在直线上;
反之一次函数可以构成等差数列,首项为,公差为.
探究新知
等差数列的通项公式与一次函数有怎样的关系
探究:已知等差数列{}中,公差为,则与有什么关系?
由等差数列的通项公式知
(这是等差数列通项公式的推广形式 )
探究新知
,
推广
探究新知
等差数列的通项公式
当.
(1)∵
例1、(1) 求等差数列 的第项.
这道题是在等差数列通项公式的四个量中,知道求.体现了等差数列通项公式中的 “知三求一”方程思想.
典例讲解
解析
说明
(2)∵
,
令,解得:.
即 是数列的第项,
.
判断一个数是否为数列的项,只须令通项公式等于这个数,得到关于的方程.若方程有正整数解,则它就是,否则不是.
典例讲解
例1、(2) 是不是等差数列 的项?如果是,是第几项?
说明
解析
典例讲解
①因为,所以数列{}是等差数列,其公差为2,
因为,所以.
②方法一:因为 ,所以,
所以,所以=3,
又因为 (),所以=3(),且.
所以数列{}是等差数列,首项为,公差为3.
解析
例2、①已知数列满足且,则_____.
②已知数列满足 (), ().
求证:数列是等差数列,并求出首项和公差.
典例讲解
②方法二:因为,且,
所以 ,
所以(),.
所以数列{}是等差数列,首项为,公差为3.
例2、①已知数列满足且,则_____.
②已知数列满足 (), ().
求证:数列是等差数列,并求出首项和公差.
①因为,所以数列{}是等差数列,其公差为2,
因为,所以.
解析
(1)作差;
(2)对差式进行变形;
(3)当是一个与无关的常数时,数列{}是等差数列;
当不是常数,是与有关的代数式时,数列{}不是等差数列.
方法归纳
定义法判定数列{}是等差数列的步骤
1.若数列的通项公式为求证:数列为等差数列.
变式训练
因为,
所以.
所以.
所以数列{}为等差数列.
证明
例3、已知 , , 成等差数列,证明: , , 成等差数列.
典例讲解
因为, , 成等差数列,所以 ,化简得,
又
,
所以, , 成等差数列.
证明
(1)涉及等差数列中相邻三项问题可用等差中项求解.
(2)在一个等差数列中,从第项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项,即;
实际上,等差数列中的某一项是与其等距离的前后两项的等差中项,
即.
方法归纳
1.等差中项的应用策略
2.等差中项法判定等差数列
若数列满足则可判定数列是等差数列.
2.已知成等差数列,试证: 也成等差数列.
变式训练
由已知成等差数列,
可得,所以,
所以,
所以,所以也成等差数列.
证明
例4、等差数列中,已知.
(1)求及通项公式;
(2)和是不是该数列中的项 若不是,说明原因;若是,是第几项
(1)在等差数列中,由,
得 解得 ,所以.
(2)由+,解得,故是第项;
由 ,得,
故不是数列中的项.
典例讲解
解析
(1)已知中的任意三个量,求出第四个量.
(2)由等差数列的通项公式可以求出该数列中的任意项,
也可以判断某一个数是不是该数列中的项.
(3)根据等差数列的两个已知条件建立关于“基本量”和的方程组,
求出和,从而确定通项公式,求得所需求的项.
(4)若数列的通项公式是关于的一次函数或常数函数,
则可判断数列是等差数列.
方法归纳
等差数列通项公式的四个主要应用
3.已知等差数列求它的通项公式及第项.
由题意可知
所以公差.
所以.
所以.
即该数列的通项公式为,第项为.
变式训练
解析
1.等差数列的定义
(1)条件:①从第__项起.
②每一项与它的_______的差都等于_______常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫做等差数列的_____,常用__表示.
前一项
同一个
公差
素养提炼
推广
素养提炼
等差数列的通项公式
当.
1.数列的通项公式,则此数列 ( )
A.是公差为的等差数列
B.是公差为的等差数列
C.是首项为的等差数列
D.是公差为的等差数列
当堂练习
解析
因为,所以,
所以
所以数列是公差为的等差数列,.所以选.
2.已知的等差中项为,则为( )
A. B. C. D.
当堂练习
3.已知等差数列则是这个数列的( )
A.第项 B.第项
C.第项 D.第项
解析
解析
因为的等差中项为,所以,所以,所以.
等差数列的首项为,公差为,所以通项公式.令,所以.
D
4.已知数列满足则此数列的通项________.
当堂练习
因为即,
所以数列是等差数列,公差为,又因为,
所以.
解析
5.等差数列中,.
(1)求的通项公式;
(2)设,求,其中表示不超过的最大整数,如,.
(1)设数列的公差为,由题意有.
解得.所以的通项公式为
(2)由知,
当时,;当时,;
当时,当时
所以.
当堂练习
解析
1.等差数列的定义:
;
2.等差数列的通项公式
.
3.等差数列的通项公式的推广
.
4.当.
归纳小结
1.教材第15页 练习:2,4,5
作 业
1.数列的定义:
按一定次序排列的一列数
2.数列的通项公式:
数列的第项与项数之间的函数关系式,即.
复习引入
人教A版同步教材名师课件
等差数列
---概念和通项公式
学习目标
学 习 目 标 核心素养
理解等差数列的概念 数学抽象
掌握等差数列通项公式的求法 数学运算
理解等差数列与一次函数的关系 直观想象
学习目标
学习目标:
1.理解等差数列的概念.
2.掌握等差数列的通项公式及应用.
3.掌握等差数列的判定方法.
学科核心素养:
1.通过学习等差中项及等差数列通项公式的应用,体现了数学运算素养.
2.借助等差数列的判断与证明,培养学生的逻辑推理素养.
研究发现我国儿童年龄在周岁之间,其标准的身高、体重大致成规律性变化:
相差
年龄 …
身高(cm)
体重(kg) …
.
引例1
探究新知
相差
你能预测岁儿童的
身高和体重吗?
,雅典举行第一届现代奥运会,到年的北京奥运会已经是第届奥运会
你能预测出第届
奥运会的时间吗?
相差
探究新知
引例2
.
请问:它们有什么共同特点?
共同特点:从第项起,每一项与它的前一项的差等于同一个常数.
定义:如果一个数列从第项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列.
探究新知
即.
1.等差数列
这个常数叫做等差数列的公差,公差通常用表示.
.
2.等差中项
(1)前提:三个数成等差数列.
(2)结论:_____叫做的等差中项.
(3)满足的关系式:________.
提示:.
探究新知
【思考】等式“” 有哪些等价形式
是
不是
不是
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项和公差, 如果不是,说明理由.
(1)
(2)
(3)
(4)
(5)
(6)
说明:判断一个数列是不是等差数列,主要是由定义进行判断:
看同一个常数.
是
是
是
新知练习
当 时,
当 时,
当 时,
说明:由定义知
数列是常数列;
数列是递增数列;
数列是递减数列.
探究新知
思 考:在这个数列中?
请试着找规律填空:
探究新知
所以
由此得到:
问题:如果已知一个等差数列的首项是 ,公差是 ,那么这个数列的通项 能求出吗?
分析1:根据等差数列的定义:
不完全归纳
(通项公式)
探究新知
由此得到:
分析2:根据等差数列的定义:
探究新知
将上面个等式相加得:
累加法
(通项公式)
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
探究新知
2.等差数列的通项公式
,当时,是一次函数,当时的函数.
等差数列的图象是点组成的集合,这些点均匀分布在直线上;
反之一次函数可以构成等差数列,首项为,公差为.
探究新知
等差数列的通项公式与一次函数有怎样的关系
探究:已知等差数列{}中,公差为,则与有什么关系?
由等差数列的通项公式知
(这是等差数列通项公式的推广形式 )
探究新知
,
推广
探究新知
等差数列的通项公式
当.
(1)∵
例1、(1) 求等差数列 的第项.
这道题是在等差数列通项公式的四个量中,知道求.体现了等差数列通项公式中的 “知三求一”方程思想.
典例讲解
解析
说明
(2)∵
,
令,解得:.
即 是数列的第项,
.
判断一个数是否为数列的项,只须令通项公式等于这个数,得到关于的方程.若方程有正整数解,则它就是,否则不是.
典例讲解
例1、(2) 是不是等差数列 的项?如果是,是第几项?
说明
解析
典例讲解
①因为,所以数列{}是等差数列,其公差为2,
因为,所以.
②方法一:因为 ,所以,
所以,所以=3,
又因为 (),所以=3(),且.
所以数列{}是等差数列,首项为,公差为3.
解析
例2、①已知数列满足且,则_____.
②已知数列满足 (), ().
求证:数列是等差数列,并求出首项和公差.
典例讲解
②方法二:因为,且,
所以 ,
所以(),.
所以数列{}是等差数列,首项为,公差为3.
例2、①已知数列满足且,则_____.
②已知数列满足 (), ().
求证:数列是等差数列,并求出首项和公差.
①因为,所以数列{}是等差数列,其公差为2,
因为,所以.
解析
(1)作差;
(2)对差式进行变形;
(3)当是一个与无关的常数时,数列{}是等差数列;
当不是常数,是与有关的代数式时,数列{}不是等差数列.
方法归纳
定义法判定数列{}是等差数列的步骤
1.若数列的通项公式为求证:数列为等差数列.
变式训练
因为,
所以.
所以.
所以数列{}为等差数列.
证明
例3、已知 , , 成等差数列,证明: , , 成等差数列.
典例讲解
因为, , 成等差数列,所以 ,化简得,
又
,
所以, , 成等差数列.
证明
(1)涉及等差数列中相邻三项问题可用等差中项求解.
(2)在一个等差数列中,从第项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等差中项,即;
实际上,等差数列中的某一项是与其等距离的前后两项的等差中项,
即.
方法归纳
1.等差中项的应用策略
2.等差中项法判定等差数列
若数列满足则可判定数列是等差数列.
2.已知成等差数列,试证: 也成等差数列.
变式训练
由已知成等差数列,
可得,所以,
所以,
所以,所以也成等差数列.
证明
例4、等差数列中,已知.
(1)求及通项公式;
(2)和是不是该数列中的项 若不是,说明原因;若是,是第几项
(1)在等差数列中,由,
得 解得 ,所以.
(2)由+,解得,故是第项;
由 ,得,
故不是数列中的项.
典例讲解
解析
(1)已知中的任意三个量,求出第四个量.
(2)由等差数列的通项公式可以求出该数列中的任意项,
也可以判断某一个数是不是该数列中的项.
(3)根据等差数列的两个已知条件建立关于“基本量”和的方程组,
求出和,从而确定通项公式,求得所需求的项.
(4)若数列的通项公式是关于的一次函数或常数函数,
则可判断数列是等差数列.
方法归纳
等差数列通项公式的四个主要应用
3.已知等差数列求它的通项公式及第项.
由题意可知
所以公差.
所以.
所以.
即该数列的通项公式为,第项为.
变式训练
解析
1.等差数列的定义
(1)条件:①从第__项起.
②每一项与它的_______的差都等于_______常数.
(2)结论:这个数列是等差数列.
(3)相关概念:这个常数叫做等差数列的_____,常用__表示.
前一项
同一个
公差
素养提炼
推广
素养提炼
等差数列的通项公式
当.
1.数列的通项公式,则此数列 ( )
A.是公差为的等差数列
B.是公差为的等差数列
C.是首项为的等差数列
D.是公差为的等差数列
当堂练习
解析
因为,所以,
所以
所以数列是公差为的等差数列,.所以选.
2.已知的等差中项为,则为( )
A. B. C. D.
当堂练习
3.已知等差数列则是这个数列的( )
A.第项 B.第项
C.第项 D.第项
解析
解析
因为的等差中项为,所以,所以,所以.
等差数列的首项为,公差为,所以通项公式.令,所以.
D
4.已知数列满足则此数列的通项________.
当堂练习
因为即,
所以数列是等差数列,公差为,又因为,
所以.
解析
5.等差数列中,.
(1)求的通项公式;
(2)设,求,其中表示不超过的最大整数,如,.
(1)设数列的公差为,由题意有.
解得.所以的通项公式为
(2)由知,
当时,;当时,;
当时,当时
所以.
当堂练习
解析
1.等差数列的定义:
;
2.等差数列的通项公式
.
3.等差数列的通项公式的推广
.
4.当.
归纳小结
1.教材第15页 练习:2,4,5
作 业
