2013-2014学年第一学期单元质量检测九年级数学试题
文档属性
| 名称 | 2013-2014学年第一学期单元质量检测九年级数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 76.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-27 11:24:23 | ||
图片预览

文档简介
2013-2014学年第一学期单元质量检测
九年级数学试题
一、选择题(每题3分,共36分)
1.下列命题中,正确的是( )
A.三点确定一个圆 B.三角形的外心在三角形的外部
C.任何一个圆都有唯一一个内接三角形 D.任何一个三角形只有一个外接圆
2.在半径为4的圆中,垂直平分半径的弦长为( )
A. B.2 C.3 D.4
3.⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么以P为圆心,且与⊙O 相切的圆的半径是( ) A.1或5 B.1 C.5 D.1或4
4.半径为1cm和2cm的两个圆外切,那么与这两个圆都相切且半径为3cm 的圆的个数是( ) A.5个 B.4个 C.3个 D.2个
5.如图,BD是⊙O的直径,∠CBD=,则∠A的度数为( ).
A.30 B.45 C.60 D.75
6.如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A.B,且O1A⊥O2A,则图中阴影部分的面积是
A.4π-8 B. 8π-16 C.16π-16 D. 16π-32
7.在中,=90°,=10,若以点为圆心,长为半径的圆恰好经过的中点,则的长等于( )
A. B.5 C. D.6
(第7题)
8.⊙O1、⊙O2、⊙O3两两外切,且半径分别为2cm,3cm,10cm,则△O1O2O3 的形状是( )
A.锐角三角形 B.等腰直角三角形; C.钝角三角形 D.直角三角形
9、甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后,甲的速度小于乙的速度;(5)甲、乙两人同时到达目的地。其中,符合图象描述的说法有( )
A、2个 B、3个 C、4个 D、5个
10、若函数是反比例函数,则的值为( )
A B C 或 D 且
11、若时,则在下列函数①,②,③,④中,值随值的增大而增大的是( )
A ①② B ②③ C ①③ D ②④
12、如图所示矩形的面积为4,则反比例函数的解析式为( )
A B C D
二、填空题(每题3分,共18分)
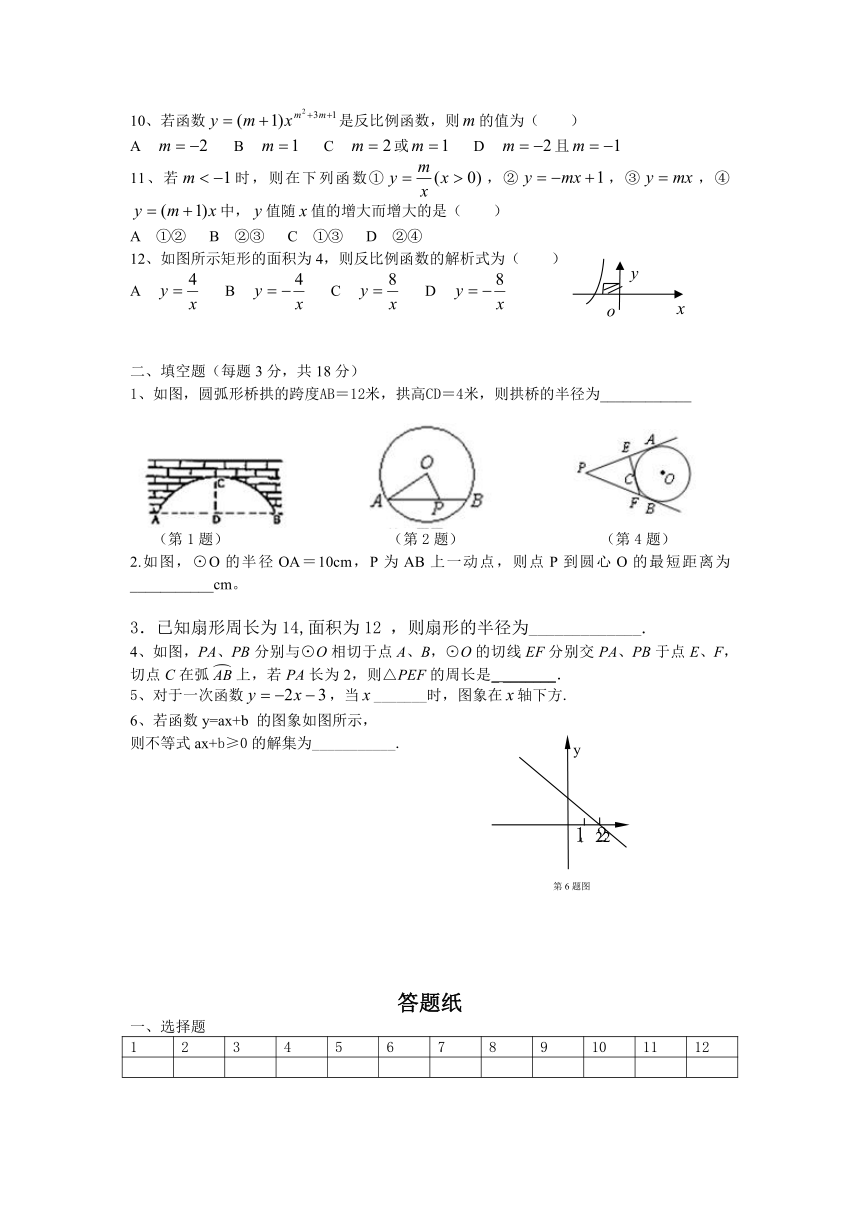
1、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为____________
(第1题) (第2题) (第4题)
2.如图,⊙O的半径OA=10cm,P为AB上一动点,则点P到圆心O的最短距离为___________cm。
3.已知扇形周长为14,面积为12 ,则扇形的半径为_____________.
4、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在弧上,若PA长为2,则△PEF的周长是_ _______.
5、对于一次函数,当_______时,图象在轴下方.
6、若函数y=ax+b 的图象如图所示,
则不等式ax+b≥0的解集为___________.
1 2
答题纸
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
二、填空题
1、______________________ 2、______________________ 3、______________________
4、______________________ 5、______________________ 6、______________________
三.解答题
1、(8分)已知反比例函数的图象经过点(,1),一次函数的图象经过点(0,3)与点,且与反比例函数的图象相交于另一点.
(1)分别求出反比例函数与一次函数的解析式.
(2)求点的坐标.
2.(8分)如图,△ABC为等腰三角形,O是底边BC的中点,圆O与腰AB相切于点D证明:AC与圆O相切
3、(8分)如图在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线过点
A(—1,0),与⊙C相切于点D,求直线的解析式。
4.(10分)如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知,.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
5、(12分)A市和B市分别库存某种机器12台和6台,现决定支援给C市10台和D市8台.已知从A市调运一台机器到C市和D市的运费分别为400元和800元;从B市调运一台机器到C市和D市的运费分别为300元和500元.
(1)设B市运往C市机器x台,求总运费W(元)关于x的函数关系式.
(2)若要求总运费不超过9000元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少?
y
1
第6题图
22
C
O
A
B
D
九年级数学试题
一、选择题(每题3分,共36分)
1.下列命题中,正确的是( )
A.三点确定一个圆 B.三角形的外心在三角形的外部
C.任何一个圆都有唯一一个内接三角形 D.任何一个三角形只有一个外接圆
2.在半径为4的圆中,垂直平分半径的弦长为( )
A. B.2 C.3 D.4
3.⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么以P为圆心,且与⊙O 相切的圆的半径是( ) A.1或5 B.1 C.5 D.1或4
4.半径为1cm和2cm的两个圆外切,那么与这两个圆都相切且半径为3cm 的圆的个数是( ) A.5个 B.4个 C.3个 D.2个
5.如图,BD是⊙O的直径,∠CBD=,则∠A的度数为( ).
A.30 B.45 C.60 D.75
6.如图,把⊙O1向右平移8个单位长度得⊙O2,两圆相交于A.B,且O1A⊥O2A,则图中阴影部分的面积是
A.4π-8 B. 8π-16 C.16π-16 D. 16π-32
7.在中,=90°,=10,若以点为圆心,长为半径的圆恰好经过的中点,则的长等于( )
A. B.5 C. D.6
(第7题)
8.⊙O1、⊙O2、⊙O3两两外切,且半径分别为2cm,3cm,10cm,则△O1O2O3 的形状是( )
A.锐角三角形 B.等腰直角三角形; C.钝角三角形 D.直角三角形
9、甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:(1)他们都行驶了18千米;(2)甲在途中停留了0.5小时;(3)乙比甲晚出发了0.5小时;(4)相遇后,甲的速度小于乙的速度;(5)甲、乙两人同时到达目的地。其中,符合图象描述的说法有( )
A、2个 B、3个 C、4个 D、5个
10、若函数是反比例函数,则的值为( )
A B C 或 D 且
11、若时,则在下列函数①,②,③,④中,值随值的增大而增大的是( )
A ①② B ②③ C ①③ D ②④
12、如图所示矩形的面积为4,则反比例函数的解析式为( )
A B C D
二、填空题(每题3分,共18分)
1、如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,则拱桥的半径为____________
(第1题) (第2题) (第4题)
2.如图,⊙O的半径OA=10cm,P为AB上一动点,则点P到圆心O的最短距离为___________cm。
3.已知扇形周长为14,面积为12 ,则扇形的半径为_____________.
4、如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在弧上,若PA长为2,则△PEF的周长是_ _______.
5、对于一次函数,当_______时,图象在轴下方.
6、若函数y=ax+b 的图象如图所示,
则不等式ax+b≥0的解集为___________.
1 2
答题纸
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
二、填空题
1、______________________ 2、______________________ 3、______________________
4、______________________ 5、______________________ 6、______________________
三.解答题
1、(8分)已知反比例函数的图象经过点(,1),一次函数的图象经过点(0,3)与点,且与反比例函数的图象相交于另一点.
(1)分别求出反比例函数与一次函数的解析式.
(2)求点的坐标.
2.(8分)如图,△ABC为等腰三角形,O是底边BC的中点,圆O与腰AB相切于点D证明:AC与圆O相切
3、(8分)如图在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线过点
A(—1,0),与⊙C相切于点D,求直线的解析式。
4.(10分)如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知,.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
5、(12分)A市和B市分别库存某种机器12台和6台,现决定支援给C市10台和D市8台.已知从A市调运一台机器到C市和D市的运费分别为400元和800元;从B市调运一台机器到C市和D市的运费分别为300元和500元.
(1)设B市运往C市机器x台,求总运费W(元)关于x的函数关系式.
(2)若要求总运费不超过9000元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少?
y
1
第6题图
22
C
O
A
B
D
同课章节目录
