代数式整式[下学期]
图片预览





文档简介
课件17张PPT。精品
中考复习方案
数学分册第一章第三课时:
代数式、整式要点、考点聚焦
课前热身
典型例题解析
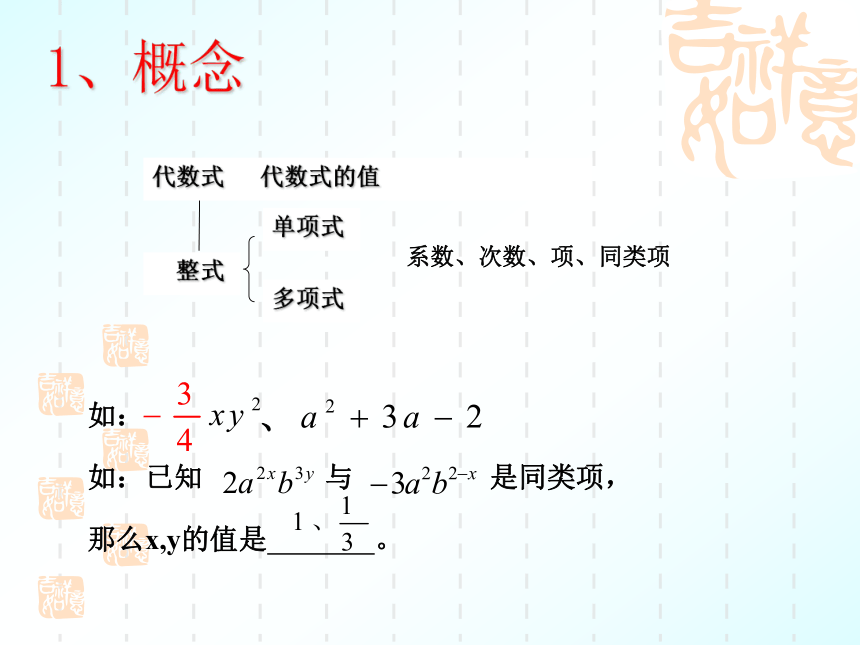
课时训练1、概念如:已知 与 是同类项,
那么x,y的值是 。
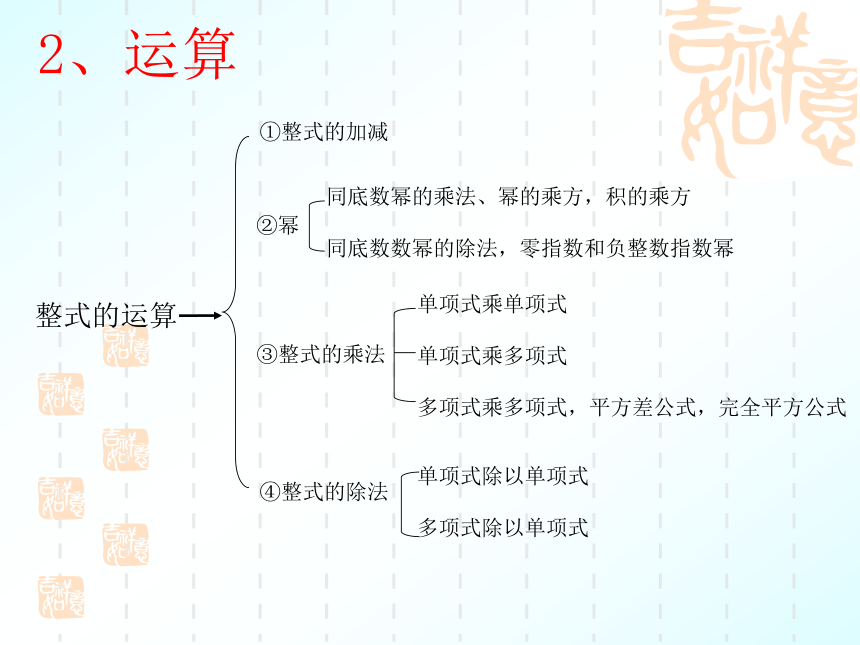
数与字母或字母与字母的积的代数式叫做单项式,单独的一个数或字母也是单项式.一个单项式中,所有字母的指数和叫做这个单项式的次数,单独一个非0数的次数是0.几个单项式的和叫做多项式.一个多项式中,次数最高的项的次数,叫做这个多项式的次数.单项式和多项式统称整式.单项式中数字因数叫做单项式的系数.2、运算要点、考点聚焦整式加减的一般步骤: 先去括号 ,再合并同类项.(去括号法则,合并同类项法则.)
[例1] (2005日照)下列运算正确的是( )
(A) (B)
(C) (D)
[例2] (2004厦门)计算:3x2y+2x2y= 。 [例3](2005四川)化简:
. [例4]化简(1)(3x+2y)(3x-2y)
(2)(2a-3b)2
课前热身2、(2004年·昆明)下列运算正确的是 ( )
A. a2·a3= a6 B. (-a+2b)2=(a-2b)2
C. D.1、(2004年·山西临汾)计算?B课前热身4、(2004年·安徽)计算:2a2 ·a3÷a4= .
2aC3、下列计算正确的是 ( )
A. 22 ·20=23=8
B. (23)2 =25 =32
C. ( ― 2)×( ― 2)2= ― 23= ― 8
D. 23÷23=2 ? 课前热身5、先化简,在求值:
[(x-y)2 +(x+y)(x-y)]÷2x,其中x=3,y=-1.5解:原式=(x2-2xy+y2+x2-y2) ÷2x
=(2x2-2xy) ÷2x
=4.56、(2004年·哈尔滨)观察下列等式:
9-1=8 16-4=12 25-9=16 36-16=20
……
这些等式反映自然数间的某种规律,设
n(n≥1)表示自然数,用关于n的等式表示这
个规律为 。【例1】
(1)多项式-2+6x+4x2是 次 项式,其中最高次项的系数是 ,常数项是 .
(2)若- x3m-1y3和- x5y2n+1是同类项,求6m-3n的值.典型例题解析解: (2)由同类项的定义可知:
二三4-2∴6m-3n=6×2-3×1=9正确区别平方差公式和完全平方公式,同时不要写成(a+b)2=a2+b2.
注意合并同类项与同底数幂相乘的区别.
如:x3+x2≠x5,而x3·x2=x5.方法小结:课时训练1、(2004年·山西临汾市)下列计算错误的是 ( )
A.a2 · a3=a6 B.3-1=1/3
C.( -3)0=1 D.2、(2004年·广西)下列运算正确的是 ( )
A.x3+x3=x6 B.x·x5=x6
C.(xy)3=xy3 D.x6÷x2=x33、(2004年·黑龙江)下列运算正确的是 ( )
A. x2·x3=x6 B.x2+x2=2x4
C.(-2x)2=4x2 D.(-2x2)(-3x3)=6x5
BAD4、(2001年·江苏连云港)在公式(a+1)2=a2+2a+1中,
当a分别取1,2,3,…,n时,可得下列几个不等式:将这n个等式的左、右两边分
别相加,可推出求和公式:
1+2+3+…+n=
(用含n的代数式表示).
(1+1)2=12+2×1+1
(2+1)2=22+2×2+1
(3+1)2=32+2×3+1
…
(n+1)2=n2+2×n+1
课时训练1.(2005四川)计算: =_____
2.(2005枣庄)下列运算正确的是( )
(A) a3+ a 3=2 a 3 (B) a 3- a 2= a
(C) a 3·a 3=2 a 6 (D) a 6÷a 2= a 3
3.(2005无锡)下列各式中,与 是同类项的是( )
A、 B、2xy C、- D、
4.(2005温州)计算:2xy+3xy=_______。
5.(2004潍坊) 计算的结果是( )
A、 B、 C、 D、
6.(2005福州)小马虎在下面的计算中只做对了一道题,他做对的题目是( )
A、 B、
C、 D、
7.(2005厦门) “比a的大1的数”用代数式表示是( )
A、 a+1 B、 a+1 C、 a D、 a-1
8.(2004海口)某商场4月份的营业额为x万元,5月份的营业额比4月份多10万元.如果该商场第二季度的营业额为4x万元,那么6月份的营业额为
万元,这个代数式的实际意义是 .
〖考题训练〗 再见!
中考复习方案
数学分册第一章第三课时:
代数式、整式要点、考点聚焦
课前热身
典型例题解析
课时训练1、概念如:已知 与 是同类项,
那么x,y的值是 。
数与字母或字母与字母的积的代数式叫做单项式,单独的一个数或字母也是单项式.一个单项式中,所有字母的指数和叫做这个单项式的次数,单独一个非0数的次数是0.几个单项式的和叫做多项式.一个多项式中,次数最高的项的次数,叫做这个多项式的次数.单项式和多项式统称整式.单项式中数字因数叫做单项式的系数.2、运算要点、考点聚焦整式加减的一般步骤: 先去括号 ,再合并同类项.(去括号法则,合并同类项法则.)
[例1] (2005日照)下列运算正确的是( )
(A) (B)
(C) (D)
[例2] (2004厦门)计算:3x2y+2x2y= 。 [例3](2005四川)化简:
. [例4]化简(1)(3x+2y)(3x-2y)
(2)(2a-3b)2
课前热身2、(2004年·昆明)下列运算正确的是 ( )
A. a2·a3= a6 B. (-a+2b)2=(a-2b)2
C. D.1、(2004年·山西临汾)计算?B课前热身4、(2004年·安徽)计算:2a2 ·a3÷a4= .
2aC3、下列计算正确的是 ( )
A. 22 ·20=23=8
B. (23)2 =25 =32
C. ( ― 2)×( ― 2)2= ― 23= ― 8
D. 23÷23=2 ? 课前热身5、先化简,在求值:
[(x-y)2 +(x+y)(x-y)]÷2x,其中x=3,y=-1.5解:原式=(x2-2xy+y2+x2-y2) ÷2x
=(2x2-2xy) ÷2x
=4.56、(2004年·哈尔滨)观察下列等式:
9-1=8 16-4=12 25-9=16 36-16=20
……
这些等式反映自然数间的某种规律,设
n(n≥1)表示自然数,用关于n的等式表示这
个规律为 。【例1】
(1)多项式-2+6x+4x2是 次 项式,其中最高次项的系数是 ,常数项是 .
(2)若- x3m-1y3和- x5y2n+1是同类项,求6m-3n的值.典型例题解析解: (2)由同类项的定义可知:
二三4-2∴6m-3n=6×2-3×1=9正确区别平方差公式和完全平方公式,同时不要写成(a+b)2=a2+b2.
注意合并同类项与同底数幂相乘的区别.
如:x3+x2≠x5,而x3·x2=x5.方法小结:课时训练1、(2004年·山西临汾市)下列计算错误的是 ( )
A.a2 · a3=a6 B.3-1=1/3
C.( -3)0=1 D.2、(2004年·广西)下列运算正确的是 ( )
A.x3+x3=x6 B.x·x5=x6
C.(xy)3=xy3 D.x6÷x2=x33、(2004年·黑龙江)下列运算正确的是 ( )
A. x2·x3=x6 B.x2+x2=2x4
C.(-2x)2=4x2 D.(-2x2)(-3x3)=6x5
BAD4、(2001年·江苏连云港)在公式(a+1)2=a2+2a+1中,
当a分别取1,2,3,…,n时,可得下列几个不等式:将这n个等式的左、右两边分
别相加,可推出求和公式:
1+2+3+…+n=
(用含n的代数式表示).
(1+1)2=12+2×1+1
(2+1)2=22+2×2+1
(3+1)2=32+2×3+1
…
(n+1)2=n2+2×n+1
课时训练1.(2005四川)计算: =_____
2.(2005枣庄)下列运算正确的是( )
(A) a3+ a 3=2 a 3 (B) a 3- a 2= a
(C) a 3·a 3=2 a 6 (D) a 6÷a 2= a 3
3.(2005无锡)下列各式中,与 是同类项的是( )
A、 B、2xy C、- D、
4.(2005温州)计算:2xy+3xy=_______。
5.(2004潍坊) 计算的结果是( )
A、 B、 C、 D、
6.(2005福州)小马虎在下面的计算中只做对了一道题,他做对的题目是( )
A、 B、
C、 D、
7.(2005厦门) “比a的大1的数”用代数式表示是( )
A、 a+1 B、 a+1 C、 a D、 a-1
8.(2004海口)某商场4月份的营业额为x万元,5月份的营业额比4月份多10万元.如果该商场第二季度的营业额为4x万元,那么6月份的营业额为
万元,这个代数式的实际意义是 .
〖考题训练〗 再见!
