18.2.1 第1课时 矩形的性质 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
18.2 特殊的平行四边形
18.2.1 矩 形
第1课时 矩形的性质
教学目标
【知识与技能】
1.理解并能说出矩形的定义和性质,理解矩形与平行四边形的区别与联系;
2.能够运用矩形的定义和性质,证明或解决有关的问题.
【过程与方法】
经历矩形中的有关问题的提出以及解题方法的探索,体会数形结合、化归等数学思想.
【情感、态度与价值观】
从学习活动中获得成功的体验,增强学习数学的自信心,培养严谨的推理能力以及自主合作精神,体会逻辑推理的思维价值.21教育网
教学重难点
【教学重点】
矩形的意义和性质,矩形与平行四边形的联系与区别.
【教学难点】
灵活应用矩形的性质证明或解决有关问题.
教学过程
一、情境导入
拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗 为什么
再次演示平行四边形的移动过程,当移动到一个角是直角时停止,观察这是什么图形
二、合作探究
探究点1 矩形的四个角都是直角
典例1 如图所示,在矩形ABCD中,AD的长为8 cm,对角线BD比AB边长4 cm.
(1)求AB的长;
(2)求点A到BD的距离AE的长.
[解析] (1)设AB为x cm,则BD为(x+4) cm.
∵四边形ABCD是矩形,∴∠BAD=90°,
∴AB2+AD2=BD2,即x2+82=(x+4)2,
解得x=6,
∴AB的长为6 cm.
(2)由(1)知BD=6 cm+4 cm=10 cm.
∵S△ABD=BD·AE=AB·AD,
∴×10×AE=×6×8,
∴AE=4.8 cm.
探究点2 矩形的对角线相等
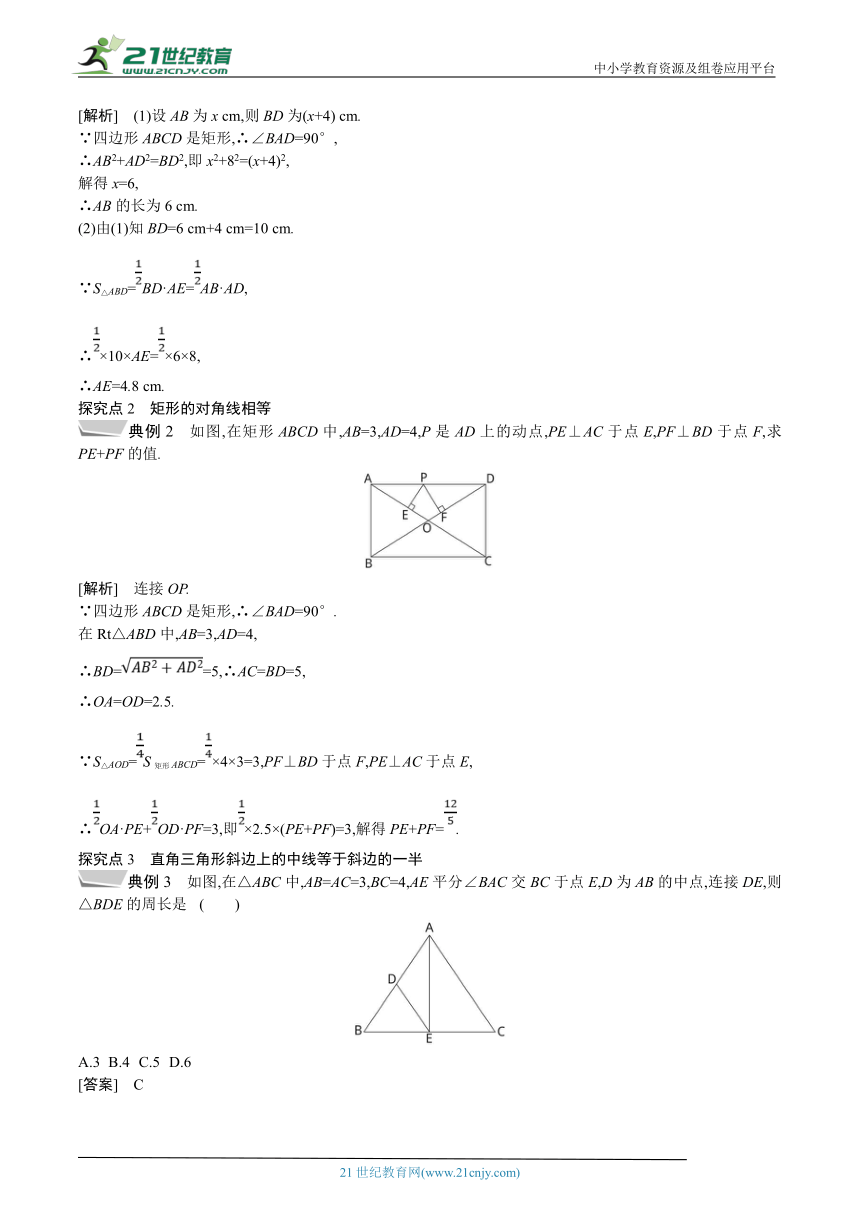
典例2 如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,求PE+PF的值.21世纪教育网版权所有
[解析] 连接OP.
∵四边形ABCD是矩形,∴∠BAD=90°.
在Rt△ABD中,AB=3,AD=4,
∴BD==5,∴AC=BD=5,
∴OA=OD=2.5.
∵S△AOD=S矩形ABCD=×4×3=3,PF⊥BD于点F,PE⊥AC于点E,
∴OA·PE+OD·PF=3,即×2.5×(PE+PF)=3,解得PE+PF=.
探究点3 直角三角形斜边上的中线等于斜边的一半
典例3 如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,D为AB的中点,连接DE,则△BDE的周长是 ( )21cnjy.com
A.3 B.4 C.5 D.6
[答案] C
三、板书设计
矩形的性质
教学反思
本节课在学生已有的认知水平上,在实际问题情境中,由学生自主探索发现矩形的性质定理,使学生经历实践、推理、交流等数学活动过程,亲身体验数学思想方法,培养学生的学习能力及运用所学知识解决问题的能力,促进学生发展.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
18.2 特殊的平行四边形
18.2.1 矩 形
第1课时 矩形的性质
教学目标
【知识与技能】
1.理解并能说出矩形的定义和性质,理解矩形与平行四边形的区别与联系;
2.能够运用矩形的定义和性质,证明或解决有关的问题.
【过程与方法】
经历矩形中的有关问题的提出以及解题方法的探索,体会数形结合、化归等数学思想.
【情感、态度与价值观】
从学习活动中获得成功的体验,增强学习数学的自信心,培养严谨的推理能力以及自主合作精神,体会逻辑推理的思维价值.21教育网
教学重难点
【教学重点】
矩形的意义和性质,矩形与平行四边形的联系与区别.
【教学难点】
灵活应用矩形的性质证明或解决有关问题.
教学过程
一、情境导入
拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗 为什么
再次演示平行四边形的移动过程,当移动到一个角是直角时停止,观察这是什么图形
二、合作探究
探究点1 矩形的四个角都是直角
典例1 如图所示,在矩形ABCD中,AD的长为8 cm,对角线BD比AB边长4 cm.
(1)求AB的长;
(2)求点A到BD的距离AE的长.
[解析] (1)设AB为x cm,则BD为(x+4) cm.
∵四边形ABCD是矩形,∴∠BAD=90°,
∴AB2+AD2=BD2,即x2+82=(x+4)2,
解得x=6,
∴AB的长为6 cm.
(2)由(1)知BD=6 cm+4 cm=10 cm.
∵S△ABD=BD·AE=AB·AD,
∴×10×AE=×6×8,
∴AE=4.8 cm.
探究点2 矩形的对角线相等
典例2 如图,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于点E,PF⊥BD于点F,求PE+PF的值.21世纪教育网版权所有
[解析] 连接OP.
∵四边形ABCD是矩形,∴∠BAD=90°.
在Rt△ABD中,AB=3,AD=4,
∴BD==5,∴AC=BD=5,
∴OA=OD=2.5.
∵S△AOD=S矩形ABCD=×4×3=3,PF⊥BD于点F,PE⊥AC于点E,
∴OA·PE+OD·PF=3,即×2.5×(PE+PF)=3,解得PE+PF=.
探究点3 直角三角形斜边上的中线等于斜边的一半
典例3 如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,D为AB的中点,连接DE,则△BDE的周长是 ( )21cnjy.com
A.3 B.4 C.5 D.6
[答案] C
三、板书设计
矩形的性质
教学反思
本节课在学生已有的认知水平上,在实际问题情境中,由学生自主探索发现矩形的性质定理,使学生经历实践、推理、交流等数学活动过程,亲身体验数学思想方法,培养学生的学习能力及运用所学知识解决问题的能力,促进学生发展.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
