18.2.2 第2课时 菱形的判定 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
第2课时 菱形的判定
教学目标
【知识与技能】
1.理解并能够说出菱形的判定定理;
2.能够运用菱形的判定定理判定菱形;
3.能够综合应用菱形的性质和判定定理,证明或解决有关的问题.
【过程与方法】
经历探索菱形判定定理的过程,发展学生实验探索的意识;形成几何分析的思路和方法.
【情感、态度与价值观】
让学生在探索过程中,加深对菱形的理解,养成主动探索的学习习惯,通过菱形与矩形判定方法的类比,进一步体会类比的思想方法.21世纪教育网版权所有
教学重难点
【教学重点】
用菱形的判定定理判定菱形.
【教学难点】
综合应用菱形的性质和判定定理,证明或解决有关的问题.
教学过程
一、情境导入
用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的“十字”,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形 21教育网
二、合作探究
探究点1 对角线互相垂直的平行四边形是菱形
典例1 如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
[解析] ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵DE=BF,∴AE=CF.
∵AE∥CF,
∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
探究点2 四条边相等的四边形是菱形
典例2 如图,在四边形ABCF中,∠ACB=90°,E是AB边的中点,点F恰好是点E关于AC所在直线的对称点.21cnjy.com
(1)证明:四边形CFAE为菱形;
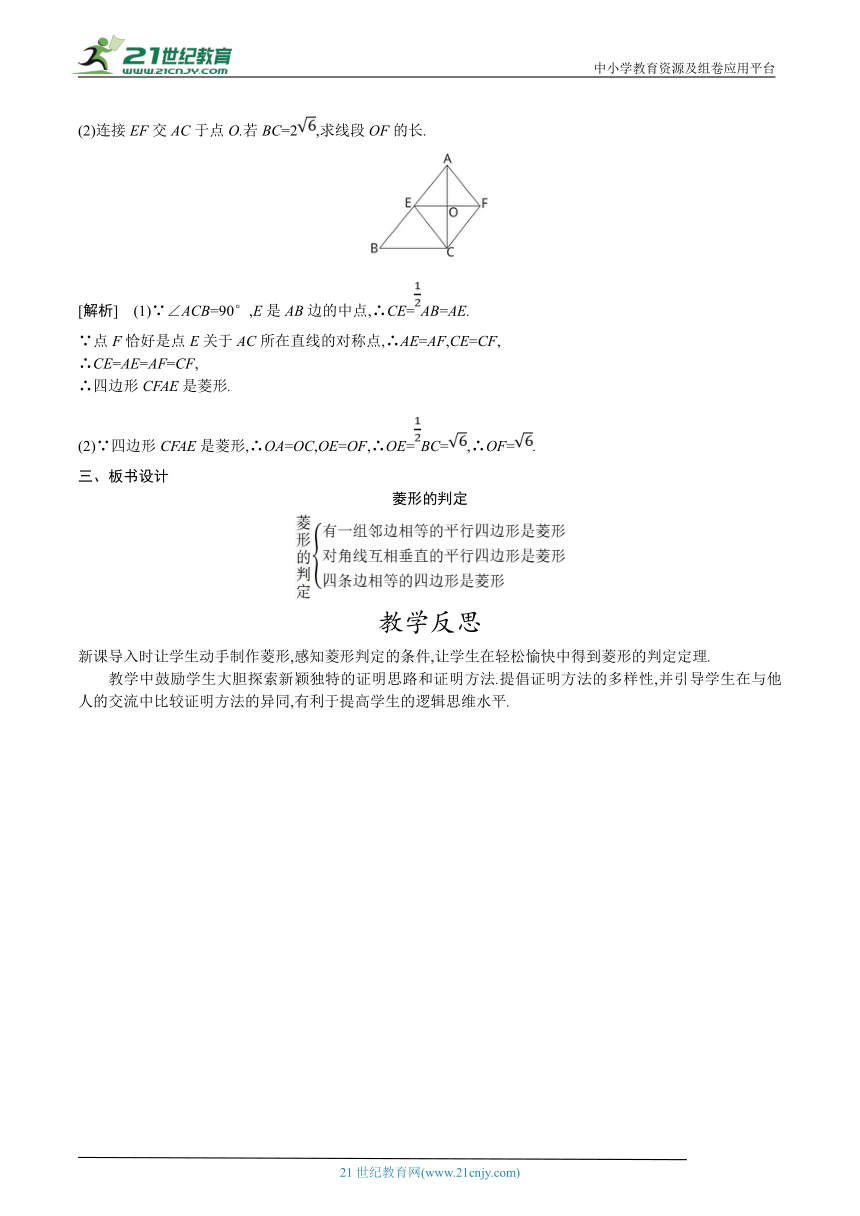
(2)连接EF交AC于点O.若BC=2,求线段OF的长.
[解析] (1)∵∠ACB=90°,E是AB边的中点,∴CE=AB=AE.
∵点F恰好是点E关于AC所在直线的对称点,∴AE=AF,CE=CF,
∴CE=AE=AF=CF,
∴四边形CFAE是菱形.
(2)∵四边形CFAE是菱形,∴OA=OC,OE=OF,∴OE=BC=,∴OF=.
三、板书设计
菱形的判定
教学反思
新课导入时让学生动手制作菱形,感知菱形判定的条件,让学生在轻松愉快中得到菱形的判定定理.
教学中鼓励学生大胆探索新颖独特的证明思路和证明方法.提倡证明方法的多样性,并引导学生在与他人的交流中比较证明方法的异同,有利于提高学生的逻辑思维水平.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第2课时 菱形的判定
教学目标
【知识与技能】
1.理解并能够说出菱形的判定定理;
2.能够运用菱形的判定定理判定菱形;
3.能够综合应用菱形的性质和判定定理,证明或解决有关的问题.
【过程与方法】
经历探索菱形判定定理的过程,发展学生实验探索的意识;形成几何分析的思路和方法.
【情感、态度与价值观】
让学生在探索过程中,加深对菱形的理解,养成主动探索的学习习惯,通过菱形与矩形判定方法的类比,进一步体会类比的思想方法.21世纪教育网版权所有
教学重难点
【教学重点】
用菱形的判定定理判定菱形.
【教学难点】
综合应用菱形的性质和判定定理,证明或解决有关的问题.
教学过程
一、情境导入
用一长一短两根木条,在它们的中点处固定一个小钉,做成一个可转动的“十字”,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形 21教育网
二、合作探究
探究点1 对角线互相垂直的平行四边形是菱形
典例1 如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
[解析] ∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵DE=BF,∴AE=CF.
∵AE∥CF,
∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
探究点2 四条边相等的四边形是菱形
典例2 如图,在四边形ABCF中,∠ACB=90°,E是AB边的中点,点F恰好是点E关于AC所在直线的对称点.21cnjy.com
(1)证明:四边形CFAE为菱形;
(2)连接EF交AC于点O.若BC=2,求线段OF的长.
[解析] (1)∵∠ACB=90°,E是AB边的中点,∴CE=AB=AE.
∵点F恰好是点E关于AC所在直线的对称点,∴AE=AF,CE=CF,
∴CE=AE=AF=CF,
∴四边形CFAE是菱形.
(2)∵四边形CFAE是菱形,∴OA=OC,OE=OF,∴OE=BC=,∴OF=.
三、板书设计
菱形的判定
教学反思
新课导入时让学生动手制作菱形,感知菱形判定的条件,让学生在轻松愉快中得到菱形的判定定理.
教学中鼓励学生大胆探索新颖独特的证明思路和证明方法.提倡证明方法的多样性,并引导学生在与他人的交流中比较证明方法的异同,有利于提高学生的逻辑思维水平.21·cn·jy·com
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
