人教A版(2019)高中数学选择性必修第二册 【整合课件】4.3.1_等比数列的概念1(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】4.3.1_等比数列的概念1(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 18:13:17 | ||
图片预览








文档简介
(共21张PPT)
§4.3.1 等比数列
目标定位
【学习目标】
1.通过类比,理解等比数列的概念并学会简单应用.
2.通过类比,掌握等比中项的概念并会应用.
3.通过类比,掌握等比数列的通项公式并了解其推导过程.
【重、难点】
重点:等比数列的定义和通项公式.
难点:等比数列与指数函数的关系.
学习目标和重难点
新知探究
(一)等比数列的概念
等比数列的定义、通项公式的推导、等比中项、等比数列与指数函数的关系等的研究方法都与等差数列相似,你能否根据研究等差数列的方法来研究等比数列呢?请尝试完成下表.
新知探究
(一)等比数列的概念
等差数列 等比数列
定 义 语言描述 如果一个数列从第2项起,数列的每一项与前一项的差都等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母d表示.
如果一个数列从第2项起,数列的每一项与前一项的比都等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母q表示.
新知探究
(一)等比数列的概念
等差数列 等比数列
定 义 符号表示 或
或
新知探究
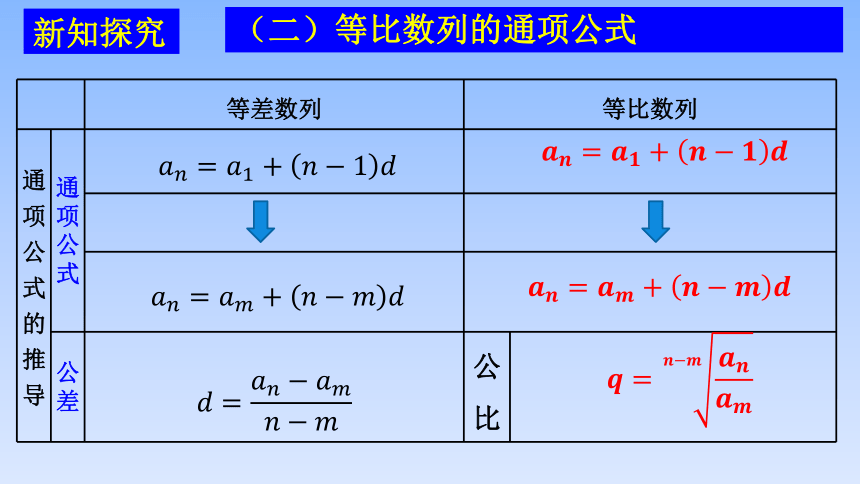
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 不完全归纳法 根据等差数列的定义,得 . ∴ , , , … , .
根据等比数列的定义,得 .
∴ ,
,
,
… ,
.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 累加法 根据等差数列的定义, ,,,…, . 将以上个等式相加,得 即 , ∴
根据等比数列的定义,,
,,…, .
将以上个等式相乘,得
, 即
∴
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 迭代法 根据等差数列的定义, .
根据等比数列的定义,
.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 通项公式
公差 公 比
新知探究
(一)等差数列前n项和与的关系
等差数列 等比数列
中 项 定义 当三个数 a,A,b成等差数列时,A叫做a与b的等差中项.
性质 2A=a+b
注意事项 任意两个数a与b都有等差中项,且等差中项是唯一的.
当三个数 a,A,b成等比数列时,A叫做a与b的等比中项.
只有当时,a与b才
有等比中项,且等比中项有
两个,它们互为相反数.
典例突破
例1. 某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84%,这种物质的半衰期为多长(精确到1年)?(放射性物质衰变到原来的一半所需时间称为这种物质的半衰期)
【解析】设这种物质最初的质量是1,经过n年,剩留量是an.
由条件可得数列{an}是一个等比数列.其中a1=0.84,q=0.84.
设an=0.5,则0.84n=0.5. 两边取对数,得nlg 0.84=lg 0.5,用计算器算得n≈4.
∴ 这种物质的半衰期大约为4年.
(一)等比数列通项公式的应用
典例突破
【解题反思】如何求解等比数列应用题?
答:求解数列应用题的关键是读懂题意,建立数学模型,弄清问题的哪一部分是数列问题,是哪种数列.在求解过程中应注意首项的确立,时间的推算.不要在运算中出现问题.
(一)等比数列通项公式的应用
典例突破
变式. 某人买了一辆价值13.5万元的新车.专家预测这种车每年
按10%的速度折旧.
(1)用一个式子表示n 年后这辆车的价值;
(2)如果他打算用满4年时卖掉这辆车,他大概能得多少钱?
【解析】(1)设n 年后这辆车的价值为,
则
(2)用满4年时,这两车的价值为
(元)
∴ 他大概能得到约元.
(一)等比数列通项公式的应用
典例突破
(二)等比数列的判定
例2. 根据下图中的框图,写出所打印数列的前5 项,并建立数列的递推公式.这个数列是等比数列吗?
【解析】若将打印出来的数依次记为a1(即A),a2,a3,… .由框图可知,
a1=1,,,,.
典例突破
(二)等比数列的判定
于是,可得递推公式,所以,
从而这个数列是等比数列,其通项公式是.
【解题反思】如何判定一个数列是否为等比数列?
要判定一个数列是等比数列,只需证明对于任意正整数n ,是一个与n无关的常数就可以了.
典例突破
变式2. 已知数列{an}的前n项和为Sn,Sn= (an-1) ().
(1) 求a1,a2;
(2) 求证:数列{an}是等比数列.
(二)等比数列的判定
【解析】(1) 由S1= (a1-1),得a1= (a1-1),解得a1=-.
又S2= (a2-1),即a1+a2= (a2-1),得a2=.
(2) 证明:当n≥2时,an=Sn-Sn-1= (an-1)- (an-1-1),
得 ∴{an}是首项为-,公比为-的等比数列.
典例突破
(三)等差比数列的项
例3. 一个等比数列的第3项与第4项分别是12与18,求它的第
1项与第2项.
【解析】 设这个等比数列的第1项是a1,公比是q,那么
a1q2=12 ……………… ①
a1q3=18 ……………… ②
由②÷①,得q=,将q=代入①,得a1=.
∴ a2=a1q=×=8.
∴ 这个数列的第1项与第2项分别是与8.
典例突破
【解题反思】在等比数列{an}中,如何求解a1,q,n,an中的量?
答:在上述四个量中,至少要知道其中的三个量,才能求其他的量,而且求解时常常利用方程思想,通过方程组解得.
(三)等比数列的项
典例突破
变式3. 在等比数列{an}中,已知a2+a5=18,a3+a6=9,求an.
【解析】∵ ,解得,a1=32.
∴ an=a1qn-1=32×n-1=26-n.
(三)等差数列的项
典例突破
例4. 已知等比数列的前三项和为168,a2-a5=42,求a5,a7
的等比中项.
【解析】设该等比数列的公比为q,首项为a1,则
, 即 ,
解得a1=96, ∴
设G是a5,a7的等比中项,则
∴ ,即a5,a7的等比中项为.
(四)等比中项的应用
典例突破
变式4. 若a,2a+2,3a+3成等比数列,求实数a的值.
【解析】∵ a,2a+2,3a+3成等比数列
∴ (2a+2)2=a(3a+3),解得a=-1,或a=-4.
当 a=-1时,2a+2,3a+3均为0,舍去.
∴ a=-4.
(四)等比中项的应用
§4.3.1 等比数列
目标定位
【学习目标】
1.通过类比,理解等比数列的概念并学会简单应用.
2.通过类比,掌握等比中项的概念并会应用.
3.通过类比,掌握等比数列的通项公式并了解其推导过程.
【重、难点】
重点:等比数列的定义和通项公式.
难点:等比数列与指数函数的关系.
学习目标和重难点
新知探究
(一)等比数列的概念
等比数列的定义、通项公式的推导、等比中项、等比数列与指数函数的关系等的研究方法都与等差数列相似,你能否根据研究等差数列的方法来研究等比数列呢?请尝试完成下表.
新知探究
(一)等比数列的概念
等差数列 等比数列
定 义 语言描述 如果一个数列从第2项起,数列的每一项与前一项的差都等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母d表示.
如果一个数列从第2项起,数列的每一项与前一项的比都等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差,通常用字母q表示.
新知探究
(一)等比数列的概念
等差数列 等比数列
定 义 符号表示 或
或
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 不完全归纳法 根据等差数列的定义,得 . ∴ , , , … , .
根据等比数列的定义,得 .
∴ ,
,
,
… ,
.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 累加法 根据等差数列的定义, ,,,…, . 将以上个等式相加,得 即 , ∴
根据等比数列的定义,,
,,…, .
将以上个等式相乘,得
, 即
∴
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 迭代法 根据等差数列的定义, .
根据等比数列的定义,
.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
通项公式的推导 通项公式
公差 公 比
新知探究
(一)等差数列前n项和与的关系
等差数列 等比数列
中 项 定义 当三个数 a,A,b成等差数列时,A叫做a与b的等差中项.
性质 2A=a+b
注意事项 任意两个数a与b都有等差中项,且等差中项是唯一的.
当三个数 a,A,b成等比数列时,A叫做a与b的等比中项.
只有当时,a与b才
有等比中项,且等比中项有
两个,它们互为相反数.
典例突破
例1. 某种放射性物质不断变化为其他物质,每经过一年剩留的这种物质是原来的84%,这种物质的半衰期为多长(精确到1年)?(放射性物质衰变到原来的一半所需时间称为这种物质的半衰期)
【解析】设这种物质最初的质量是1,经过n年,剩留量是an.
由条件可得数列{an}是一个等比数列.其中a1=0.84,q=0.84.
设an=0.5,则0.84n=0.5. 两边取对数,得nlg 0.84=lg 0.5,用计算器算得n≈4.
∴ 这种物质的半衰期大约为4年.
(一)等比数列通项公式的应用
典例突破
【解题反思】如何求解等比数列应用题?
答:求解数列应用题的关键是读懂题意,建立数学模型,弄清问题的哪一部分是数列问题,是哪种数列.在求解过程中应注意首项的确立,时间的推算.不要在运算中出现问题.
(一)等比数列通项公式的应用
典例突破
变式. 某人买了一辆价值13.5万元的新车.专家预测这种车每年
按10%的速度折旧.
(1)用一个式子表示n 年后这辆车的价值;
(2)如果他打算用满4年时卖掉这辆车,他大概能得多少钱?
【解析】(1)设n 年后这辆车的价值为,
则
(2)用满4年时,这两车的价值为
(元)
∴ 他大概能得到约元.
(一)等比数列通项公式的应用
典例突破
(二)等比数列的判定
例2. 根据下图中的框图,写出所打印数列的前5 项,并建立数列的递推公式.这个数列是等比数列吗?
【解析】若将打印出来的数依次记为a1(即A),a2,a3,… .由框图可知,
a1=1,,,,.
典例突破
(二)等比数列的判定
于是,可得递推公式,所以,
从而这个数列是等比数列,其通项公式是.
【解题反思】如何判定一个数列是否为等比数列?
要判定一个数列是等比数列,只需证明对于任意正整数n ,是一个与n无关的常数就可以了.
典例突破
变式2. 已知数列{an}的前n项和为Sn,Sn= (an-1) ().
(1) 求a1,a2;
(2) 求证:数列{an}是等比数列.
(二)等比数列的判定
【解析】(1) 由S1= (a1-1),得a1= (a1-1),解得a1=-.
又S2= (a2-1),即a1+a2= (a2-1),得a2=.
(2) 证明:当n≥2时,an=Sn-Sn-1= (an-1)- (an-1-1),
得 ∴{an}是首项为-,公比为-的等比数列.
典例突破
(三)等差比数列的项
例3. 一个等比数列的第3项与第4项分别是12与18,求它的第
1项与第2项.
【解析】 设这个等比数列的第1项是a1,公比是q,那么
a1q2=12 ……………… ①
a1q3=18 ……………… ②
由②÷①,得q=,将q=代入①,得a1=.
∴ a2=a1q=×=8.
∴ 这个数列的第1项与第2项分别是与8.
典例突破
【解题反思】在等比数列{an}中,如何求解a1,q,n,an中的量?
答:在上述四个量中,至少要知道其中的三个量,才能求其他的量,而且求解时常常利用方程思想,通过方程组解得.
(三)等比数列的项
典例突破
变式3. 在等比数列{an}中,已知a2+a5=18,a3+a6=9,求an.
【解析】∵ ,解得,a1=32.
∴ an=a1qn-1=32×n-1=26-n.
(三)等差数列的项
典例突破
例4. 已知等比数列的前三项和为168,a2-a5=42,求a5,a7
的等比中项.
【解析】设该等比数列的公比为q,首项为a1,则
, 即 ,
解得a1=96, ∴
设G是a5,a7的等比中项,则
∴ ,即a5,a7的等比中项为.
(四)等比中项的应用
典例突破
变式4. 若a,2a+2,3a+3成等比数列,求实数a的值.
【解析】∵ a,2a+2,3a+3成等比数列
∴ (2a+2)2=a(3a+3),解得a=-1,或a=-4.
当 a=-1时,2a+2,3a+3均为0,舍去.
∴ a=-4.
(四)等比中项的应用
