人教A版(2019)高中数学选择性必修第二册 【整合课件】4.3.1_等比数列的概念2(共21张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】4.3.1_等比数列的概念2(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
§4.3.1 等比数列
目标定位
【学习目标】
1.结合等差数列的性质,类比出等比数列的性质.
2.理解等比数列的性质.
3.掌握等比数列的性质并能综合应用.
【重、难点】
重点:理解等比数列的性质.
难点:掌握等比数列的性质并能综合应用.
学习目标和重难点
新知探究
(一)等比数列的概念
等比数列的性质的研究方法与等差数列的性质的研究方法也是相似的,你能否根据研究等差数列也通过类比的方法来研究等比数列的性质呢?请尝试完成下表.
新知探究
(一)与函数的关系类比
等差数列 等比数列
与 函 数 的 关 系 图像 当 时, 是关于序号n 的一次函数,其图象是直线 上一系列孤立的点,d 为该直线的斜率,a1-d是该直线在y轴上的截距.
当 时, 是关于序号n的指数型函数,其图像是曲线,上一系列孤立的点.
新知探究
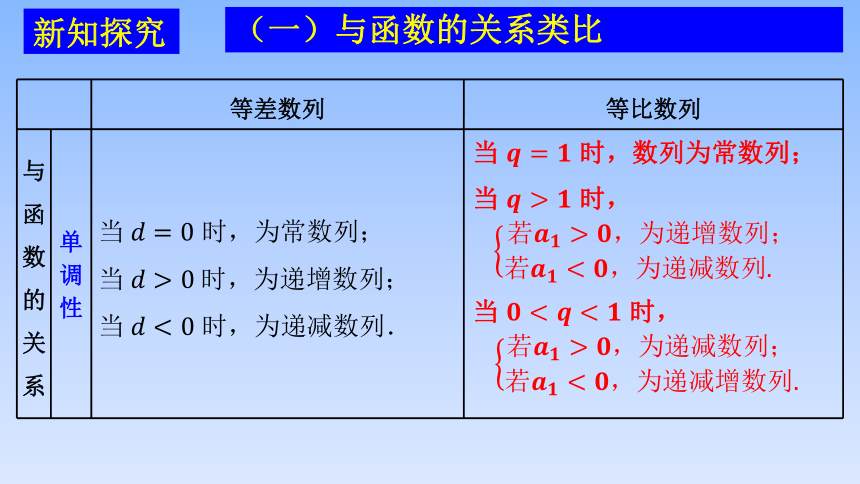
(一)与函数的关系类比
等差数列 等比数列
与 函 数 的 关 系 单调性 当 时,为常数列; 当 时,为递增数列; 当 时,为递减数列.
当 时,数列为常数列;
当 时,
当 时,
新知探究
(二)性质类比
等差数列 等比数列
数列中的项与序号的关系 性质1 若m+n=p+q,则 am+an=ap+aq . 特别地,若m+n=2p,则 am+an=2ap .
若m+n=s+t,则
.
特别地,若m+n=2p,则
.
证明:左边
右边
又m+n=s+t ∴ 左边
新知探究
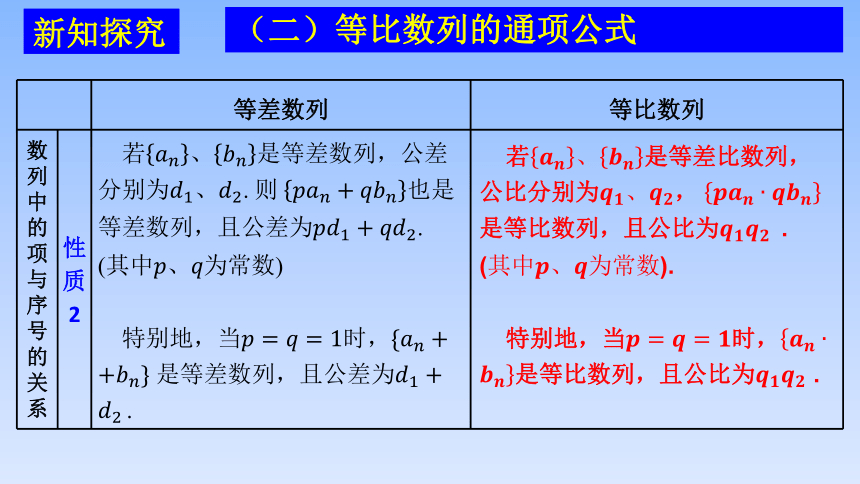
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质2 若是等差数列,公差 分别为. . () 特别地,当时, 是等差数列,且公差为 .
若是等差比数列,公比分别为,
是等比数列,且公比为. ().
特别地,当时,
是等比数列,且公比为 .
新知探究
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质3 若是等差数列,公差为.则也是等差数列,且公差为.
若是等比数列,公比为,则也是等差数列,且公比仍为.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质4 若数列{an}和{kn}都是等差数列,公差分别为,则 也是等差数列,且公差为.
若数列{an}是等比数列,公比为,{kn}是等差数列,公差为,则 是等比数列,且公比为.
典例突破
例1. 已知是互异的正数, 是
的等差中项, 是的正的等比
中项,则 与 的大小关系是( )
A. B.
C. D.无法确定
(一)等比数列通项公式与指数函数的关系
A
a
b
A
B
1
2
3
n
O
【解析】若则由等差数列和等
比数列与函数的关系,由两个数列的
图像(如图)
. 易得;
同样,若也有. 故选A.
典例突破
变式1. 在1,4两个数之间插入两个数,使它们成等差数
列,再在1,4两个数之间插入两个数,使它们成
等比数列,则下列关系正确的是( )
A. B.
C. D.
(一)等比数列通项公式的应用
B
典例突破
例2. 若等比数列{an}中,a3=2,a11=8,则a7=________.
【解析】∵ {an}是等比数列 ∴
又 ∴
(二)等比数列性质的应用1
典例突破
(二)等比数列性质的应用1
【解题反思】等比数列{an}中,利用等比中项求某一项时,如
何确定该项的符号?
答:等比数列{an}中,奇数项的符号一定相同,偶数项的符号一定相同. 所以,要确定某项的符号,只需看同类的项(奇数项或偶数项)的符号. 如果没有同类的项的符号,就要根据公比的正负判断.
典例突破
(二)等比数列性质的应用1
变式2.(1)若a5=2,a15=8,则a10=_____.
(2)在 和 之间插入三个数,使这五个数成等比数列,
则插入的三个数的乘积为____________.
【解析】 (2)
设插入的三个数依次为a2,a3,a4,其中设a1=,a5=.
∵ 这5个数成等比数列 ∴ a2a3a4=.
又 =a1a5=×=36,a3>0 ∴ a3=
∴ a2a3a4==63=216.
216
典例突破
(三)等比数列性质的应用2
例3. 等比数列{an}的各项均为正数,且,,则
_____.
【解析】∵ 得
∴ ∴
∴ ∴
又 ∴ 是首项为,公差为1的等差数列
∴ .
25
典例突破
(三)等比数列性质的应用2
【解题反思】若数列{an}是正项等比数列,{an}是等差数列
吗?若是,首项和公差各是多少?若不是,请说明理由.
答:{an}一定是等差数列,首项是a1,公差是
()
典例突破
(三)等比数列性质的应用2
变式3. 已知{an}是在正项等比数列,则下列说法正确的是
__________.
① 数列{a}是等比数列; ② 数列{2an}是等比数列;
③ 数列{lgan}是等比数列; ④ 数列{nan}是等比数列;
⑤ 数列{an+ an+1 }是等比数列; ⑥ 数列是等比数列.
①②⑤⑥
典例突破
(四)等差、等比数列的综合应用
例4. 有四个实数,前三个数依次成等比,它们的积是-8,后三
个数依次成等差,它们的积为-80,求出这四个数.
【解析】由题意设这四个数为,b,bq,a,则有
,解得或,
∴ 这四个数为1,-2,4,10或,-2,-5,-8.
典例突破
(四)等差、等比数列的综合应用
【解题反思】当几个数成等比数列时,如何设最合适?
答:(1)三个数成等比数列,常设为,a,aq (a≠0).
(2)四个数成等比数列,常设为a,aq,aq2,aq3 (a≠0),而不
设为,,aq,aq3,因为这样设会因等比数列的公比为
q2而失根.
典例突破
(四)等差、等比数列的综合应用
变式4. 三个互不相等的数成等差数列,如果适当排列三个数,
又可成为等比数列,这三个数的和为6,则这三个数为
________.
【解析】由已知,设这三个数为a-d,a,a+d,
则a-d+a+a+d=6,解得 a=2,
∴ 这三个数可表示为2-d,2,2+d,
-4,2,8
典例突破
(四)等差、等比数列的综合应用
① 若2-d为等比中项,则有(2-d)2=2(2+d),解之得d=6,
或d=0(舍去).此时三个数为-4,2,8.
② 若2+d是等比中项,则有(2+d)2=2(2-d),解之得d=-6,
或d=0(舍去).此时三个数为8,2,-4.
③ 若2为等比中项,则22=(2+d)·(2-d), 解之得 d=0(舍).
综上可知此三数为-4,2,8.
§4.3.1 等比数列
目标定位
【学习目标】
1.结合等差数列的性质,类比出等比数列的性质.
2.理解等比数列的性质.
3.掌握等比数列的性质并能综合应用.
【重、难点】
重点:理解等比数列的性质.
难点:掌握等比数列的性质并能综合应用.
学习目标和重难点
新知探究
(一)等比数列的概念
等比数列的性质的研究方法与等差数列的性质的研究方法也是相似的,你能否根据研究等差数列也通过类比的方法来研究等比数列的性质呢?请尝试完成下表.
新知探究
(一)与函数的关系类比
等差数列 等比数列
与 函 数 的 关 系 图像 当 时, 是关于序号n 的一次函数,其图象是直线 上一系列孤立的点,d 为该直线的斜率,a1-d是该直线在y轴上的截距.
当 时, 是关于序号n的指数型函数,其图像是曲线,上一系列孤立的点.
新知探究
(一)与函数的关系类比
等差数列 等比数列
与 函 数 的 关 系 单调性 当 时,为常数列; 当 时,为递增数列; 当 时,为递减数列.
当 时,数列为常数列;
当 时,
当 时,
新知探究
(二)性质类比
等差数列 等比数列
数列中的项与序号的关系 性质1 若m+n=p+q,则 am+an=ap+aq . 特别地,若m+n=2p,则 am+an=2ap .
若m+n=s+t,则
.
特别地,若m+n=2p,则
.
证明:左边
右边
又m+n=s+t ∴ 左边
新知探究
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质2 若是等差数列,公差 分别为. . () 特别地,当时, 是等差数列,且公差为 .
若是等差比数列,公比分别为,
是等比数列,且公比为. ().
特别地,当时,
是等比数列,且公比为 .
新知探究
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质3 若是等差数列,公差为.则也是等差数列,且公差为.
若是等比数列,公比为,则也是等差数列,且公比仍为.
新知探究
(二)等比数列的通项公式
等差数列 等比数列
数列中的项与序号的关系 性质4 若数列{an}和{kn}都是等差数列,公差分别为,则 也是等差数列,且公差为.
若数列{an}是等比数列,公比为,{kn}是等差数列,公差为,则 是等比数列,且公比为.
典例突破
例1. 已知是互异的正数, 是
的等差中项, 是的正的等比
中项,则 与 的大小关系是( )
A. B.
C. D.无法确定
(一)等比数列通项公式与指数函数的关系
A
a
b
A
B
1
2
3
n
O
【解析】若则由等差数列和等
比数列与函数的关系,由两个数列的
图像(如图)
. 易得;
同样,若也有. 故选A.
典例突破
变式1. 在1,4两个数之间插入两个数,使它们成等差数
列,再在1,4两个数之间插入两个数,使它们成
等比数列,则下列关系正确的是( )
A. B.
C. D.
(一)等比数列通项公式的应用
B
典例突破
例2. 若等比数列{an}中,a3=2,a11=8,则a7=________.
【解析】∵ {an}是等比数列 ∴
又 ∴
(二)等比数列性质的应用1
典例突破
(二)等比数列性质的应用1
【解题反思】等比数列{an}中,利用等比中项求某一项时,如
何确定该项的符号?
答:等比数列{an}中,奇数项的符号一定相同,偶数项的符号一定相同. 所以,要确定某项的符号,只需看同类的项(奇数项或偶数项)的符号. 如果没有同类的项的符号,就要根据公比的正负判断.
典例突破
(二)等比数列性质的应用1
变式2.(1)若a5=2,a15=8,则a10=_____.
(2)在 和 之间插入三个数,使这五个数成等比数列,
则插入的三个数的乘积为____________.
【解析】 (2)
设插入的三个数依次为a2,a3,a4,其中设a1=,a5=.
∵ 这5个数成等比数列 ∴ a2a3a4=.
又 =a1a5=×=36,a3>0 ∴ a3=
∴ a2a3a4==63=216.
216
典例突破
(三)等比数列性质的应用2
例3. 等比数列{an}的各项均为正数,且,,则
_____.
【解析】∵ 得
∴ ∴
∴ ∴
又 ∴ 是首项为,公差为1的等差数列
∴ .
25
典例突破
(三)等比数列性质的应用2
【解题反思】若数列{an}是正项等比数列,{an}是等差数列
吗?若是,首项和公差各是多少?若不是,请说明理由.
答:{an}一定是等差数列,首项是a1,公差是
()
典例突破
(三)等比数列性质的应用2
变式3. 已知{an}是在正项等比数列,则下列说法正确的是
__________.
① 数列{a}是等比数列; ② 数列{2an}是等比数列;
③ 数列{lgan}是等比数列; ④ 数列{nan}是等比数列;
⑤ 数列{an+ an+1 }是等比数列; ⑥ 数列是等比数列.
①②⑤⑥
典例突破
(四)等差、等比数列的综合应用
例4. 有四个实数,前三个数依次成等比,它们的积是-8,后三
个数依次成等差,它们的积为-80,求出这四个数.
【解析】由题意设这四个数为,b,bq,a,则有
,解得或,
∴ 这四个数为1,-2,4,10或,-2,-5,-8.
典例突破
(四)等差、等比数列的综合应用
【解题反思】当几个数成等比数列时,如何设最合适?
答:(1)三个数成等比数列,常设为,a,aq (a≠0).
(2)四个数成等比数列,常设为a,aq,aq2,aq3 (a≠0),而不
设为,,aq,aq3,因为这样设会因等比数列的公比为
q2而失根.
典例突破
(四)等差、等比数列的综合应用
变式4. 三个互不相等的数成等差数列,如果适当排列三个数,
又可成为等比数列,这三个数的和为6,则这三个数为
________.
【解析】由已知,设这三个数为a-d,a,a+d,
则a-d+a+a+d=6,解得 a=2,
∴ 这三个数可表示为2-d,2,2+d,
-4,2,8
典例突破
(四)等差、等比数列的综合应用
① 若2-d为等比中项,则有(2-d)2=2(2+d),解之得d=6,
或d=0(舍去).此时三个数为-4,2,8.
② 若2+d是等比中项,则有(2+d)2=2(2-d),解之得d=-6,
或d=0(舍去).此时三个数为8,2,-4.
③ 若2为等比中项,则22=(2+d)·(2-d), 解之得 d=0(舍).
综上可知此三数为-4,2,8.
