人教A版(2019)数学必修第一册5.5.1.1两角差的余弦公式 课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册5.5.1.1两角差的余弦公式 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 902.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 20:21:41 | ||
图片预览






文档简介
(共27张PPT)
5.5.1.1 两角差的余弦公式
高一
必修一
本节目标
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
任务一:知识预习
课前预习
预习课本P215~217,思考并完成以下问题
(1)如何用α的三角函数与β的三角函数表示cos(α-β)
(2)两角差的余弦公式是如何推导的?
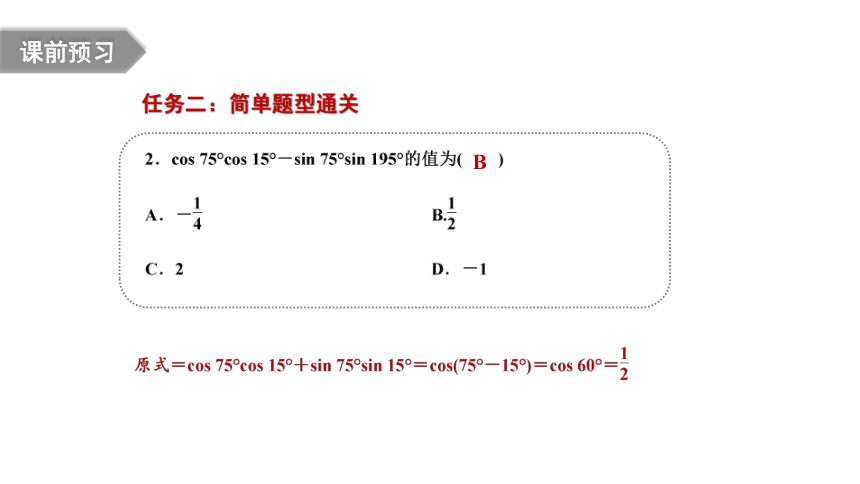
任务二:简单题型通关
课前预习
B
课前预习
任务二:简单题型通关
B
课前预习
任务二:简单题型通关
新知精讲
两角差的余弦公式
公式 cos(α-β)=___________________
简记符号 C(α-β)
使用条件 α,β为任意角
cos αcos β+sin αsin β
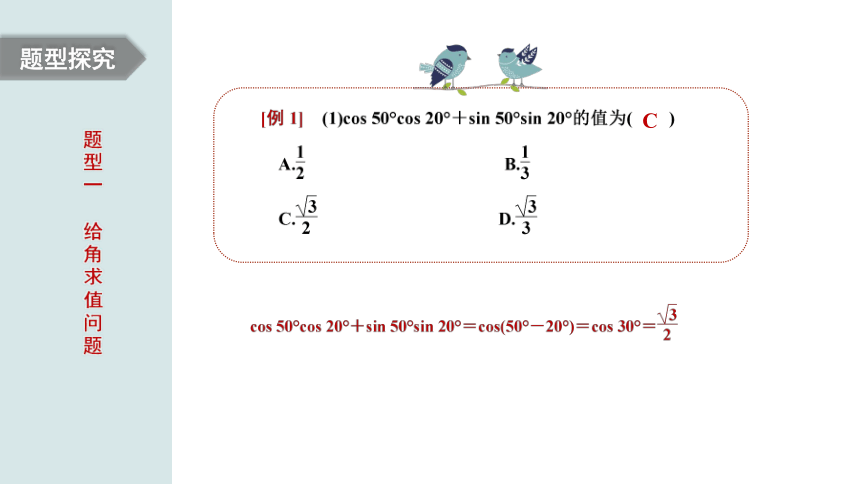
题型探究
题型一
给角求值问题
C
题型探究
题型一
给角求值问题
C
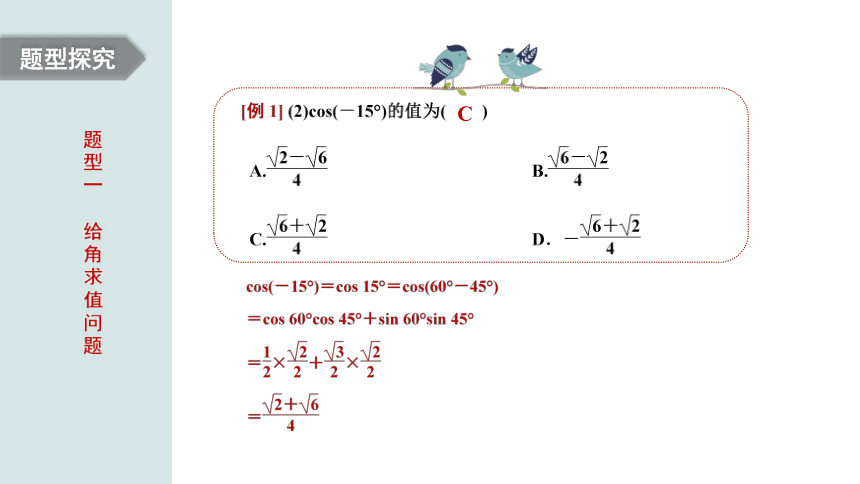
题型探究
题型一
给角求值问题
[例1] (3)化简cos(α+45°)cos α+sin(α+45°)sin α=________.
归纳总结
利用公式C(α-β)求值的方法技巧
在利用两角差的余弦公式解含有非特殊角的三角函数式的求值问题时,要先把非特殊角转化为特殊角的差(或同一个非特殊角与特殊角的差),再用公式直接化简求值,在转化过程中,充分利用诱导公式,构造出两角差的余弦公式的结构形式,正确地顺用公式或逆用公式求值.
技巧总结
活学活用
1. 计算下列各式的值:
(1)cos 56°cos 26°+sin 56°sin 26°;
(2)cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°).
题型探究
题型二
给值求值问题
题型探究
题型二
给值求值问题
归纳总结
给值求值的解题策略
(1)已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.常见角的变换有:
解题策略
活学活用
题型探究
题型三
给值求角问题
题型探究
题型三
给值求角问题
题型探究
一题多变
1.[变条件] 若本例(1)中“sin α”变为“cos α”,“sin β ”变为“cos β ”,则α-β=________.
-
题型探究
一题多变
归纳总结
已知三角函数值求角的解题步骤
(1)界定角的范围.
(2)求所求角的某种三角函数值
(为防止增解最好选取在上述范围内单调的三角函数).
(3)结合三角函数值及角的范围求角.
解题策略
达标检测
A
达标检测
2.化简:cos(-42°)cos 18°+sin 42°sin(-18°)=________.
达标检测
达标检测
本课小结
1.两角差的余弦公式是什么?
2.利用公式C(α-β)求值的方法技巧.
3.已知三角函数值求角的解题步骤.
再见
5.5.1.1 两角差的余弦公式
高一
必修一
本节目标
1.熟悉两角差的余弦公式的推导过程.
2.熟记两角差的余弦公式,并能灵活运用.
任务一:知识预习
课前预习
预习课本P215~217,思考并完成以下问题
(1)如何用α的三角函数与β的三角函数表示cos(α-β)
(2)两角差的余弦公式是如何推导的?
任务二:简单题型通关
课前预习
B
课前预习
任务二:简单题型通关
B
课前预习
任务二:简单题型通关
新知精讲
两角差的余弦公式
公式 cos(α-β)=___________________
简记符号 C(α-β)
使用条件 α,β为任意角
cos αcos β+sin αsin β
题型探究
题型一
给角求值问题
C
题型探究
题型一
给角求值问题
C
题型探究
题型一
给角求值问题
[例1] (3)化简cos(α+45°)cos α+sin(α+45°)sin α=________.
归纳总结
利用公式C(α-β)求值的方法技巧
在利用两角差的余弦公式解含有非特殊角的三角函数式的求值问题时,要先把非特殊角转化为特殊角的差(或同一个非特殊角与特殊角的差),再用公式直接化简求值,在转化过程中,充分利用诱导公式,构造出两角差的余弦公式的结构形式,正确地顺用公式或逆用公式求值.
技巧总结
活学活用
1. 计算下列各式的值:
(1)cos 56°cos 26°+sin 56°sin 26°;
(2)cos(α-35°)cos(α+25°)+sin(α-35°)sin(α+25°).
题型探究
题型二
给值求值问题
题型探究
题型二
给值求值问题
归纳总结
给值求值的解题策略
(1)已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.常见角的变换有:
解题策略
活学活用
题型探究
题型三
给值求角问题
题型探究
题型三
给值求角问题
题型探究
一题多变
1.[变条件] 若本例(1)中“sin α”变为“cos α”,“sin β ”变为“cos β ”,则α-β=________.
-
题型探究
一题多变
归纳总结
已知三角函数值求角的解题步骤
(1)界定角的范围.
(2)求所求角的某种三角函数值
(为防止增解最好选取在上述范围内单调的三角函数).
(3)结合三角函数值及角的范围求角.
解题策略
达标检测
A
达标检测
2.化简:cos(-42°)cos 18°+sin 42°sin(-18°)=________.
达标检测
达标检测
本课小结
1.两角差的余弦公式是什么?
2.利用公式C(α-β)求值的方法技巧.
3.已知三角函数值求角的解题步骤.
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
