人教A版(2019)数学必修第一册期末复习: 函数的单调性与最值 课件(共30张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册期末复习: 函数的单调性与最值 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 869.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
函数的单调性与最值
期 末
复 习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
1.函数的单调性
核心考点
①增函数与减函数
②单调区间
注意事项
求单调区间或讨论单调性必须先求定义域
一个函数的同一种单调区间用“和”或“,”连接,不能用“∪”连接
函数在某个区间上单调时,在整个定义域上不一定就单调
如函数y=
核心考点
1.函数的单调性
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 ①对于任意的x∈I,都有f(x)≤M ②存在x0∈I,使得f(x0)=M ①对于任意x∈I,都有f(x)≥M
②存在x0∈I,使得f(x0)=M
结论 M为函数y=f(x)的最大值 M为函数y=f(x)的最小值
核心考点
2.函数的最值
若函数f(x),g(x)在区间I上具有单调性,则在区间I上具有以下性质:
(1) f(x)与a·f(x)在a>0时具有相同的单调性,在a<0时具有相反的单调性.
(2) f(x),g(x)都是增(减)函数,则f(x)+g(x)是增(减)函数.
(3) 当f(x),g(x)都是增(减)函数时
若两者都恒大于零,则f(x)·g(x)也是增(减)函数;
若两者都恒小于零,则f(x)·g(x)是减(增)函数.
常用结论
核心考点
重 要
结 论
复合函数 y=f [g(x)]的单调性:同增异减
开区间上的“单峰”函数一定存在最大值(最小值)
1.下列函数中,在区间(0,1)上是增函数的是( )
A.y=|x| B.y=3-x
C.y= D.y=-x2+4
A
R上递减
(0,+∞)递减
(0,+∞)递减
过关检测
y=-x递减
y=递减
f(x)=-x+ 递减
f(x)的最大值为f(-2)=
A
过关检测
3.若函数f(x)满足“对任意的x1,x2∈R,当x1<x2时,都有f(x1)>f(x2)”,则满足f(2x-1)<f(1)的实数x的取值范围为__________.
对任意的x1,x2∈R,当x1<x2时,都有f(x1)>f(x2)
函数f(x)在定义域内为减函数
f(2x-1)<f(1)
2x-1>1
x>1
(1,+∞)
过关检测
题型一
确定函数的单调性
考法(一) 确定不含参函数的单调性(区间)
例1 函数f(x)=|x2-3x+2|的单调递增区间是( )
A. B. 和[2,+∞)
C.(-∞,1]和 D. 和[2,+∞)
常考题型
如图所示,函数的单调递增区间是和[2,+∞)
B
例2 函数y=的单调递增区间为__________,单调递减区间为____________.
常考题型
题型一
确定函数的单调性
考法(一) 确定不含参函数的单调性(区间)
令u=x2+x-6
u≥0
u=x2+x-6在(-∞,-3]上是减函数,在[2,+∞)上是增函数
y=在[0,+∞)上是增函数
y= 的单调递减区间为(-∞,-3],单调递增区间为[2,+∞)
x≤-3或x≥2
[2,+∞)
(-∞,-3]
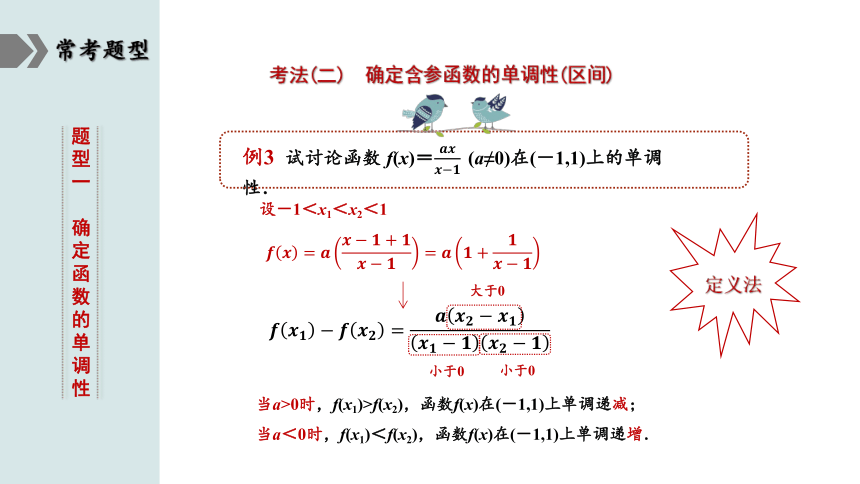
例3 试讨论函数 f(x)=(a≠0)在(-1,1)上的单调性.
考法(二) 确定含参函数的单调性(区间)
常考题型
题型一
确定函数的单调性
设-1<x1<x2<1
大于0
小于0
小于0
当a>0时,f(x1)>f(x2),函数f(x)在(-1,1)上单调递减;
当a<0时,f(x1)<f(x2),函数f(x)在(-1,1)上单调递增.
定义法
确定函数单调性的方法
定义法
图象法
性质法
①对于和、差构成的函数,根据各初等函数的增减性及f(x)±g(x)增减性判断;
②对于复合函数,根据 “同增异减”判断
技巧点拨
令t=
函数的定义域为[0,1]
g(t)=是减函数
t= 的单调递减区间为
原函数的单调递增区间为
D
过关检测
2.判断函数f(x)=x+(a>0)在(0,+∞)上的单调性.
设x1,x2是任意两个正数,且x1<x2
f(x1)-f(x2)=(x1x2-a).
当0<x1<x2≤时
0<x1x2<a,x1-x2<0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数f(x)在(0, ]上是减函数;
当≤x1<x2时
x1x2>a,x1-x2<0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
所以函数f(x)在[,+∞)上是增函数.
过关检测
题型二
函数单调性的应用
考法(一) 比较函数值的大小
例4 已知函数f(x)的图象关于直线x=1对称,当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,设a=f,b=f(2),c=f(e),则a,b,c的大小关系为( )
A.c>a>b B.c>b>a C.a>c>b D.b>a>c
常考题型
f(x)的图象关于直线x=1对称
f= f
x2>x1>1时,[f(x2)-f(x1)]·(x2-x1)<0恒成立
f(x)在(1,+∞)上单调递减
1<2<<e
f(2)>f >f(e)
b>a>c
D
考法(二) 解函数不等式
例5 已知函数f(x)为R上的减函数,则满足<f(1)的实数x的取值范围是 ( )
A.(-1,1) B.(0,1)
C.(-1,0)∪(0,1) D.(-∞,-1)∪(1,+∞)
题型二
函数单调性的应用
常考题型
f(x)为R上的减函数
<f(1)
>1,且x≠0
-1<x<0或0<x<1
C
考法(三) 利用函数的单调性求参数
例6 若f(x)=是定义在R上的减函数,则a的取值范围为________.
题型二
函数单调性的应用
常考题型
看个性
找共性
技巧点拨
看个性
考法(一)比较函数值的大小
考法(二)求解与函数单调性有关的抽象函数不等式
考法(三)是在考法(一)(二)基础上的更深一步拓展
根据函数的性质将自变量转化到同一单调区间上
利用单调性比较大小
利用函数的单调性将“f ”符号脱掉
转化为具体的不等式求解
根据单调性把问题转化为单调区间关系
技巧点拨
找共性
1.明确函数在定义域内的单调性
2.利用单调性,结合已知,把要求问题转化为易处理问题
3.求解转化后的问题,得结果
技巧点拨
1.已知函数f(x)=log2x+,若x1∈(1,2),x2∈(2,+∞),则 ( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
(1,+∞)上为增函数,且f(2)=0
x1∈(1,2)时,f(x1)<f(2)=0
x2∈(2,+∞)时,f(x2)>f(2)=0
f(x1)<0,f(x2)>0
B
过关检测
2.设函数f(x)=,若函数f(x)在区间(a,a+1)上单调递增,则实数a的取值范围是 ( )
A.(-∞,1] B.[1,4]
C.[4,+∞) D.(-∞,1]∪[4,+∞)
由图象可知,若f(x)在(a,a+1)上单调递增,需满足a≥4或a+1≤2,
即a≤1或a≥4.
D
过关检测
题型
三
函数的最值或值域
例7 函数y=的值域为________.
x2≥0
-1≤y<1
[-1,1)
常考题型
例8 函数f(x)=的最大值为________.
x≥1时,函数f(x)=为减函数
f(x)在x=1处取得最大值,为f(1)=1
x<1时,函数f(x)=-x2+2在x=0处取得最大值,为f(0)=2
故函数f(x)的最大值为2
2
题型
三
函数的最值或值域
常考题型
求最值的
常用方法
单调性法
图象法
基本不等式法
技巧点拨
1.函数f(x)=在区间[a,b]上的最大值是1,最小值是,则a+b=________.
6
f(x)在[a,b]上为减函数
单调性法
过关检测
2.函数y=-x(x≥0)的最大值为________.
令t=,则t≥0
y=t-t2=
当t=,即x=时,ymax=
过关检测
3.设0<x<,则函数y=4x(3-2x)的最大值为________.
当且仅当2x=3-2x,即x=时,等号成立.
∈
基本不等式法
过关检测
再见
函数的单调性与最值
期 末
复 习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
1.函数的单调性
核心考点
①增函数与减函数
②单调区间
注意事项
求单调区间或讨论单调性必须先求定义域
一个函数的同一种单调区间用“和”或“,”连接,不能用“∪”连接
函数在某个区间上单调时,在整个定义域上不一定就单调
如函数y=
核心考点
1.函数的单调性
前提 设函数y=f(x)的定义域为I,如果存在实数M满足 条件 ①对于任意的x∈I,都有f(x)≤M ②存在x0∈I,使得f(x0)=M ①对于任意x∈I,都有f(x)≥M
②存在x0∈I,使得f(x0)=M
结论 M为函数y=f(x)的最大值 M为函数y=f(x)的最小值
核心考点
2.函数的最值
若函数f(x),g(x)在区间I上具有单调性,则在区间I上具有以下性质:
(1) f(x)与a·f(x)在a>0时具有相同的单调性,在a<0时具有相反的单调性.
(2) f(x),g(x)都是增(减)函数,则f(x)+g(x)是增(减)函数.
(3) 当f(x),g(x)都是增(减)函数时
若两者都恒大于零,则f(x)·g(x)也是增(减)函数;
若两者都恒小于零,则f(x)·g(x)是减(增)函数.
常用结论
核心考点
重 要
结 论
复合函数 y=f [g(x)]的单调性:同增异减
开区间上的“单峰”函数一定存在最大值(最小值)
1.下列函数中,在区间(0,1)上是增函数的是( )
A.y=|x| B.y=3-x
C.y= D.y=-x2+4
A
R上递减
(0,+∞)递减
(0,+∞)递减
过关检测
y=-x递减
y=递减
f(x)=-x+ 递减
f(x)的最大值为f(-2)=
A
过关检测
3.若函数f(x)满足“对任意的x1,x2∈R,当x1<x2时,都有f(x1)>f(x2)”,则满足f(2x-1)<f(1)的实数x的取值范围为__________.
对任意的x1,x2∈R,当x1<x2时,都有f(x1)>f(x2)
函数f(x)在定义域内为减函数
f(2x-1)<f(1)
2x-1>1
x>1
(1,+∞)
过关检测
题型一
确定函数的单调性
考法(一) 确定不含参函数的单调性(区间)
例1 函数f(x)=|x2-3x+2|的单调递增区间是( )
A. B. 和[2,+∞)
C.(-∞,1]和 D. 和[2,+∞)
常考题型
如图所示,函数的单调递增区间是和[2,+∞)
B
例2 函数y=的单调递增区间为__________,单调递减区间为____________.
常考题型
题型一
确定函数的单调性
考法(一) 确定不含参函数的单调性(区间)
令u=x2+x-6
u≥0
u=x2+x-6在(-∞,-3]上是减函数,在[2,+∞)上是增函数
y=在[0,+∞)上是增函数
y= 的单调递减区间为(-∞,-3],单调递增区间为[2,+∞)
x≤-3或x≥2
[2,+∞)
(-∞,-3]
例3 试讨论函数 f(x)=(a≠0)在(-1,1)上的单调性.
考法(二) 确定含参函数的单调性(区间)
常考题型
题型一
确定函数的单调性
设-1<x1<x2<1
大于0
小于0
小于0
当a>0时,f(x1)>f(x2),函数f(x)在(-1,1)上单调递减;
当a<0时,f(x1)<f(x2),函数f(x)在(-1,1)上单调递增.
定义法
确定函数单调性的方法
定义法
图象法
性质法
①对于和、差构成的函数,根据各初等函数的增减性及f(x)±g(x)增减性判断;
②对于复合函数,根据 “同增异减”判断
技巧点拨
令t=
函数的定义域为[0,1]
g(t)=是减函数
t= 的单调递减区间为
原函数的单调递增区间为
D
过关检测
2.判断函数f(x)=x+(a>0)在(0,+∞)上的单调性.
设x1,x2是任意两个正数,且x1<x2
f(x1)-f(x2)=(x1x2-a).
当0<x1<x2≤时
0<x1x2<a,x1-x2<0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数f(x)在(0, ]上是减函数;
当≤x1<x2时
x1x2>a,x1-x2<0,所以f(x1)-f(x2)<0,即f(x1)<f(x2),
所以函数f(x)在[,+∞)上是增函数.
过关检测
题型二
函数单调性的应用
考法(一) 比较函数值的大小
例4 已知函数f(x)的图象关于直线x=1对称,当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,设a=f,b=f(2),c=f(e),则a,b,c的大小关系为( )
A.c>a>b B.c>b>a C.a>c>b D.b>a>c
常考题型
f(x)的图象关于直线x=1对称
f= f
x2>x1>1时,[f(x2)-f(x1)]·(x2-x1)<0恒成立
f(x)在(1,+∞)上单调递减
1<2<<e
f(2)>f >f(e)
b>a>c
D
考法(二) 解函数不等式
例5 已知函数f(x)为R上的减函数,则满足<f(1)的实数x的取值范围是 ( )
A.(-1,1) B.(0,1)
C.(-1,0)∪(0,1) D.(-∞,-1)∪(1,+∞)
题型二
函数单调性的应用
常考题型
f(x)为R上的减函数
<f(1)
>1,且x≠0
-1<x<0或0<x<1
C
考法(三) 利用函数的单调性求参数
例6 若f(x)=是定义在R上的减函数,则a的取值范围为________.
题型二
函数单调性的应用
常考题型
看个性
找共性
技巧点拨
看个性
考法(一)比较函数值的大小
考法(二)求解与函数单调性有关的抽象函数不等式
考法(三)是在考法(一)(二)基础上的更深一步拓展
根据函数的性质将自变量转化到同一单调区间上
利用单调性比较大小
利用函数的单调性将“f ”符号脱掉
转化为具体的不等式求解
根据单调性把问题转化为单调区间关系
技巧点拨
找共性
1.明确函数在定义域内的单调性
2.利用单调性,结合已知,把要求问题转化为易处理问题
3.求解转化后的问题,得结果
技巧点拨
1.已知函数f(x)=log2x+,若x1∈(1,2),x2∈(2,+∞),则 ( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
(1,+∞)上为增函数,且f(2)=0
x1∈(1,2)时,f(x1)<f(2)=0
x2∈(2,+∞)时,f(x2)>f(2)=0
f(x1)<0,f(x2)>0
B
过关检测
2.设函数f(x)=,若函数f(x)在区间(a,a+1)上单调递增,则实数a的取值范围是 ( )
A.(-∞,1] B.[1,4]
C.[4,+∞) D.(-∞,1]∪[4,+∞)
由图象可知,若f(x)在(a,a+1)上单调递增,需满足a≥4或a+1≤2,
即a≤1或a≥4.
D
过关检测
题型
三
函数的最值或值域
例7 函数y=的值域为________.
x2≥0
-1≤y<1
[-1,1)
常考题型
例8 函数f(x)=的最大值为________.
x≥1时,函数f(x)=为减函数
f(x)在x=1处取得最大值,为f(1)=1
x<1时,函数f(x)=-x2+2在x=0处取得最大值,为f(0)=2
故函数f(x)的最大值为2
2
题型
三
函数的最值或值域
常考题型
求最值的
常用方法
单调性法
图象法
基本不等式法
技巧点拨
1.函数f(x)=在区间[a,b]上的最大值是1,最小值是,则a+b=________.
6
f(x)在[a,b]上为减函数
单调性法
过关检测
2.函数y=-x(x≥0)的最大值为________.
令t=,则t≥0
y=t-t2=
当t=,即x=时,ymax=
过关检测
3.设0<x<,则函数y=4x(3-2x)的最大值为________.
当且仅当2x=3-2x,即x=时,等号成立.
∈
基本不等式法
过关检测
再见
同课章节目录
