人教A版(2019)数学必修第一册期末复习:函数的奇偶性与周期性 课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册期末复习:函数的奇偶性与周期性 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 719.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
函数的奇偶性与周期性
期末
复习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
奇偶性 定义 图象特点
偶函数 如果对于f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)叫偶函数
关于y轴对称
奇函数 如果对于f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)叫奇函数
关于原点对称
核心考点
1.函数的奇偶性
奇偶性的5个重要结论
(1)若一个奇函数f(x)在原点处有定义,那么一定有f(0)=0.
(2)若函数f(x)是偶函数,那么f(x)=f(-x)=f(|x|).
(3)既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.
(4)奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.
(5)偶函数在关于原点对称的区间上有相同的最大(小)值,取最值时的自变量互为相反数;
奇函数在关于原点对称的区间上的最值互为相反数,取最值时的自变量也互为相反数.
核心考点
周期性的4个
常用结论
若f (x+a)=-f (x),则函数的周期为2a
若f (x+a)=,则函数的周期为2a
若f (x+a)=- ,则函数的周期为2a
若f (x+a)=f (x-a),则周期为2a
核心考点
若y=f (x+a)是偶函数,则y=f (x)的图象关于直线x=a对称
若对于R上的任意 x 都有f (2a-x)=f (x)或f (-x)=f (2a+x),则y=f(x)的图象关于直线x=a对称
若y=f (x+b)是奇函数,则函数y=f (x)关于点(b,0)中心对称
对称性的3个常用结论
核心考点
1.下列函数中为偶函数的是 ( )
A.y=x2sin x B.y=x2cos x
C.y=|ln x| D.y=2-x
奇
偶
非奇非偶
非奇非偶
B
过关检测
2.若y=f(x)(x∈R)是奇函数,则下列坐标表示的点一定在y=f(x)图象上的是 ( )
A.(a,-f(a)) B.(-a,-f(a))
C.(-a,-f(-a)) D.(a,f(-a))
y=f(x)是奇函数
图象关于原点对称
(a,f(a))是y=f(x)图象上的点
(-a,-f(a))一定在y=f(x)的图象上
B
过关检测
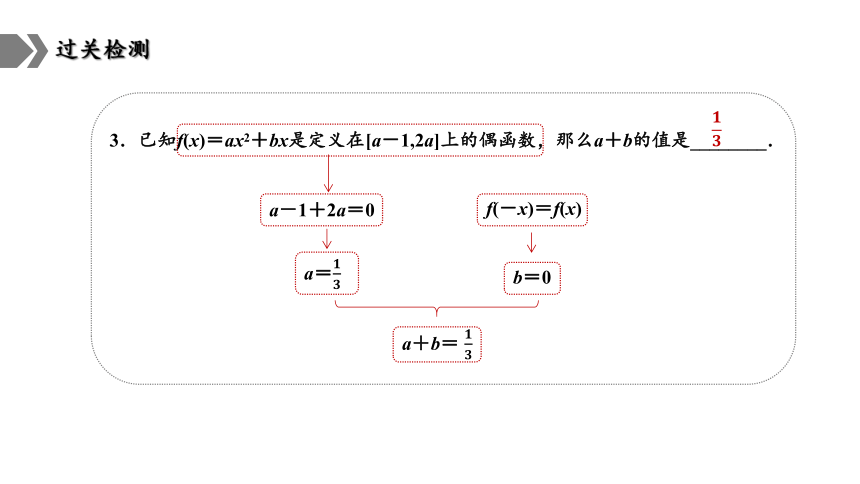
3.已知f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,那么a+b的值是________.
a-1+2a=0
a=
f(-x)=f(x)
b=0
a+b=
过关检测
4.设f(x)是定义在R上的周期为2的函数,当x∈[-1,1)时,f(x)=, 则f =________.
1
过关检测
题型一
函数奇偶性的判定
例1 判断下列函数的奇偶性
(1)f(x)=(x+1) ;
(2)
常考题型
-1<x≤1
f(x)的定义域不关于原点对称
f(x)为非奇非偶函数
所以f(x)为奇函数.
-x<0,f(-x) =x2-2x-1=-f(x)
-x>0,f(-x) =-x2-2x+1=-f(x)
当x>0时,f(x)=-x2+2x+1
当x<0时,f(x)=x2+2x-1
定义法
题型一
函数奇偶性的判定
例1 判断下列函数的奇偶性
(1)f(x)=(x+1) ;
(2)
常考题型
-1<x≤1
f(x)的定义域不关于原点对称
f(x)为非奇非偶函数
图象法
由奇函数的图象关于原点对称的特征知函数f(x)为奇函数
判断奇偶性的
3种方法
图象法
性质法
定义法
技巧点拨
定义法
第二步:验证f(-x)=±f(x)
第一步:判断定义域是否关于原点对称
技巧点拨
图象法
技巧点拨
设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:
奇+奇=奇,奇×奇=偶,
偶+偶=偶,偶×偶=偶,
奇×偶=奇.
分段函数只有当对称的两个区间上满足相同关系时,分段函数才具有确定的奇偶性。
技巧点拨
性质法
易错提示
题型二
函数奇偶性的应用
例2 (广州调研)已知函数f(x)=+a为奇函数,则实数a=________.
f(x)的定义域为(-∞,0)∪(0,+∞)
f(x)为奇函数
f(-x)=-f(x)
+a= ﹣a
2a=﹣
常考题型
例3 函数f(x)在R上为奇函数,且x>0时,f(x)=x+1,则当x<0时,f(x)=________.
x-1
x>0时,f(x)=x+1
当x<0时,-x>0
f(x)=-f(-x)=-(-x+1)=x-1
f(x)为奇函数
题型二
函数奇偶性的应用
常考题型
例4 已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2017)+f(2019)的值为________.
g(-x)=f(-x-1)
g(-x)=-g(x),f(-x)=f(x)
f(x-1)=-f(x+1)
f(x-1)+f(x+1)=0
f(2017)+f(2019)=f(2018-1)+f(2018+1)=0
0
题型二
函数奇偶性的应用
常考题型
函数奇偶性问题的解题策略
利用奇函数、偶函数的定义求解
特殊值法求解
x=0处有定义的奇函数 f(x),可考虑 f(0)=0
求函数解析式:将待求区间上的自变量转化到已知区间上,再用奇偶性求
求解析式中的参数值
求函数值:用奇偶性将待求值转化为已知区间上的函数值求解
技巧点拨
1.设f(x)-x2=g(x),x∈R,若函数f(x)为偶函数,则g(x)的解析式可以为 ( )
A.g(x)=x3 B.g(x)=cos x
C.g(x)=1+x D.g(x)=xex
B
f(x)=x2+g(x)
f(x)为偶函数
(-x)2+g(-x)=x2+g(x)
g(-x)=g(x)
g(x)为偶函数
过关检测
2.设函数f(x)=,若f(x)是奇函数,则g(3)的值是 ( )
A.1 B.3 C.-3 D.-1
C
f(x)是奇函数
f(-3)=-f(3)
f(x)=
log2(1+3)=-(g(3)+1)
g(3)=-3
过关检测
3.若关于x的函数f(x)=(t≠0)的最大值为a,最小值为b,且a+b=2,则t=________.
f(x)==
设g(x)=
g(x)为奇函数
g(x)max+g(x)min=0
g(x)max=a-t
g(x)min=b-t
a+b-2t=0
a+b=2
t=1
1
过关检测
题型
三
函数的周期性
例5 设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2019)=________.
f(x+2)=f(x)
当x∈[0,2)时,f(x)=2x-x2
f(x)的周期T=2
f(0)=0,f(1)=1
f(0)=f(2)=f(4)=…=f(2 018)=0
f(1)=f(3)=f(5)=…=f(2 019)=1
f(0)+f(1)+f(2)+…+f(2019)=1010
1010
常考题型
函数周期性有关问题的求解策略
(1)求解与函数的周期性有关的问题,应根据题目特征及周期定义,求出函数的周期.
(2)周期函数的图象具有周期性,如果发现一个函数的图象具有两个对称性(注意:对称中心在平行于x轴的直线上,对称轴平行于y轴),那么这个函数一定具有周期性.
技巧点拨
1.已知函数f(x)的定义域为R,当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>时,,则f(6)等于 ( )
A.-2 B.-1 C.0 D.2
D
当x>时,
周期为1
f(6)=f(1)=-f(-1)=-[(-1)3-1]=2
过关检测
题型
四
函数性质的综合应用
考法(一) 单调性与奇偶性综合
例6 (石家庄质检)已知f(x)为奇函数,且当x>0时,f(x)单调递增,f(1)=0,若f(x-1)>0,则x的取值范围为( )
A.{x|0<x<1或x>2} B.{x|x<0或x>2}
C.{x|x<0或x>3} D.{x|x<-1或x>1}
常考题型
例6 (石家庄质检)已知f(x)为奇函数,且当x>0时,f(x)单调递增,f(1)=0,若f(x-1)>0,则x的取值范围为 ( )
A.{x|0<x<1或x>2} B.{x|x<0或x>2}
C.{x|x<0或x>3}
D.{x|x<-1或x>1}
f(x)的示意图
A
f(x-1)>0
-1<x-1<0或x-1>1
0<x<1或x>2
f(x)为奇函数
f(-1)=-f(1)=0
f(x)在(0,+∞)上单调递增
常考题型
考法(二) 奇偶性与周期性综合
例7 (赣州月考)定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为 ( )
A.(-∞,-3) B.(3,+∞)
C.(-∞,-1) D.(1,+∞)
题型
四
函数性质的综合应用
常考题型
例7 (2019·赣州月考)定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为 ( )
A.(-∞,-3)
B.(3,+∞)
C.(-∞,-1)
D.(1,+∞)
D
f(x+3)=f(x)
f(x)是定义在R上的以3为周期的函数
f(7)=f(7-9)=f(-2)
函数f(x)是偶函数
f(-2)=f(2)
f(7)=f(2)>1
a>1
常考题型
考法(三) 单调性、奇偶性与周期性综合
例8 (达州模拟)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[-1,0]上单调递减,设a=f(-2.8),b=f(-1.6), c=f(0.5),则a,b,c的大小关系是 ( )
A.a>b>c B.c>a>b
C.b>c>a D.a>c>b
题型
四
函数性质的综合应用
常考题型
例8 (达州模拟)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[-1,0]上单调递减,设a=f(-2.8),b=f(-1.6), c=f(0.5),则a,b,c的大小关系是 ( )
A.a>b>c
B.c>a>b
C.b>c>a
D.a>c>b
D
f(x+2)=f(x)
函数的周期为2
a=f(-2.8)=f(-0.8)
b=f(-1.6)=f(0.4)=f(-0.4)
c=f(0.5)=f(-0.5)
函数f(x)在 [-1,0]上单调递减
a>c>b
常考题型
考法(一) 已知函数单调递增且为奇函数,求自变量范围,有时也比较大小
常利用奇、偶函数图象的对称性;
考法(二)已知f(x)是周期函数且为偶函数,求函数值的范围
常利用奇偶性及周期性进行转换,将所求函数值的自变量转化到已知解析式的函数定义域内求解;
考法(三)函数周期性、奇偶性与单调性结合
解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.
技巧点拨
1.已知f(x)是定义在R上的偶函数,且f(x+1)=-f(x),若f(x)在[-1,0]上单调递减,则f(x)在[1,3]上是 ( )
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
D
f(x+1)=-f(x)
f(x+2)=-f(x+1)=f(x)
f(x)的周期是2
f(x)在定义域R上是偶函数
在[-1,0]上是减函数
f(x)在[0,1]上是增函数
f(x)在[1,2]上是减函数在[2,3]上是增函数
f(x)在[1,3]上是先减后增的函数
过关检测
2.(2018·全国卷Ⅱ)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)= ( )
A.-50 B.0
C.2 D.50
f(x)是奇函数
f(1-x)=-f(x-1)
f(1-x)=f(1+x)
-f(x-1)=f(x+1)
f(x+2)=-f(x)
f(x+4)=-f(x+2)=f(x)
f(1-x)=f(1+x)
f(x)的图象关于直线x=1对称
f(2)=f(0)=0
f(-2)=0
f(1)=2
f(-1)=-2
f(1)+f(2)+f(3)+f(4)=f(1)+f(2)+f(-1)+f(0)=0
C
f(1)+f(2)+f(3)+f(4)+…+f(49)+f(50)=0×12+f(49)+f(50)=f(1)+f(2) =2
周期为4
过关检测
3.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f(-),则a的取值范围是________.
f(x)在(0,+∞)上单调递减,f(- )=f()
f(2|a-1|)>f(-)
f(2|a-1|)>f()
2|a-1|< =
|a-1|<
过关检测
再见
函数的奇偶性与周期性
期末
复习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
奇偶性 定义 图象特点
偶函数 如果对于f(x)定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)叫偶函数
关于y轴对称
奇函数 如果对于f(x)定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)叫奇函数
关于原点对称
核心考点
1.函数的奇偶性
奇偶性的5个重要结论
(1)若一个奇函数f(x)在原点处有定义,那么一定有f(0)=0.
(2)若函数f(x)是偶函数,那么f(x)=f(-x)=f(|x|).
(3)既是奇函数又是偶函数的函数只有一种类型,即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.
(4)奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.
(5)偶函数在关于原点对称的区间上有相同的最大(小)值,取最值时的自变量互为相反数;
奇函数在关于原点对称的区间上的最值互为相反数,取最值时的自变量也互为相反数.
核心考点
周期性的4个
常用结论
若f (x+a)=-f (x),则函数的周期为2a
若f (x+a)=,则函数的周期为2a
若f (x+a)=- ,则函数的周期为2a
若f (x+a)=f (x-a),则周期为2a
核心考点
若y=f (x+a)是偶函数,则y=f (x)的图象关于直线x=a对称
若对于R上的任意 x 都有f (2a-x)=f (x)或f (-x)=f (2a+x),则y=f(x)的图象关于直线x=a对称
若y=f (x+b)是奇函数,则函数y=f (x)关于点(b,0)中心对称
对称性的3个常用结论
核心考点
1.下列函数中为偶函数的是 ( )
A.y=x2sin x B.y=x2cos x
C.y=|ln x| D.y=2-x
奇
偶
非奇非偶
非奇非偶
B
过关检测
2.若y=f(x)(x∈R)是奇函数,则下列坐标表示的点一定在y=f(x)图象上的是 ( )
A.(a,-f(a)) B.(-a,-f(a))
C.(-a,-f(-a)) D.(a,f(-a))
y=f(x)是奇函数
图象关于原点对称
(a,f(a))是y=f(x)图象上的点
(-a,-f(a))一定在y=f(x)的图象上
B
过关检测
3.已知f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,那么a+b的值是________.
a-1+2a=0
a=
f(-x)=f(x)
b=0
a+b=
过关检测
4.设f(x)是定义在R上的周期为2的函数,当x∈[-1,1)时,f(x)=, 则f =________.
1
过关检测
题型一
函数奇偶性的判定
例1 判断下列函数的奇偶性
(1)f(x)=(x+1) ;
(2)
常考题型
-1<x≤1
f(x)的定义域不关于原点对称
f(x)为非奇非偶函数
所以f(x)为奇函数.
-x<0,f(-x) =x2-2x-1=-f(x)
-x>0,f(-x) =-x2-2x+1=-f(x)
当x>0时,f(x)=-x2+2x+1
当x<0时,f(x)=x2+2x-1
定义法
题型一
函数奇偶性的判定
例1 判断下列函数的奇偶性
(1)f(x)=(x+1) ;
(2)
常考题型
-1<x≤1
f(x)的定义域不关于原点对称
f(x)为非奇非偶函数
图象法
由奇函数的图象关于原点对称的特征知函数f(x)为奇函数
判断奇偶性的
3种方法
图象法
性质法
定义法
技巧点拨
定义法
第二步:验证f(-x)=±f(x)
第一步:判断定义域是否关于原点对称
技巧点拨
图象法
技巧点拨
设f(x),g(x)的定义域分别是D1,D2,那么在它们的公共定义域上:
奇+奇=奇,奇×奇=偶,
偶+偶=偶,偶×偶=偶,
奇×偶=奇.
分段函数只有当对称的两个区间上满足相同关系时,分段函数才具有确定的奇偶性。
技巧点拨
性质法
易错提示
题型二
函数奇偶性的应用
例2 (广州调研)已知函数f(x)=+a为奇函数,则实数a=________.
f(x)的定义域为(-∞,0)∪(0,+∞)
f(x)为奇函数
f(-x)=-f(x)
+a= ﹣a
2a=﹣
常考题型
例3 函数f(x)在R上为奇函数,且x>0时,f(x)=x+1,则当x<0时,f(x)=________.
x-1
x>0时,f(x)=x+1
当x<0时,-x>0
f(x)=-f(-x)=-(-x+1)=x-1
f(x)为奇函数
题型二
函数奇偶性的应用
常考题型
例4 已知f(x)是定义在R上的偶函数,g(x)是定义在R上的奇函数,且g(x)=f(x-1),则f(2017)+f(2019)的值为________.
g(-x)=f(-x-1)
g(-x)=-g(x),f(-x)=f(x)
f(x-1)=-f(x+1)
f(x-1)+f(x+1)=0
f(2017)+f(2019)=f(2018-1)+f(2018+1)=0
0
题型二
函数奇偶性的应用
常考题型
函数奇偶性问题的解题策略
利用奇函数、偶函数的定义求解
特殊值法求解
x=0处有定义的奇函数 f(x),可考虑 f(0)=0
求函数解析式:将待求区间上的自变量转化到已知区间上,再用奇偶性求
求解析式中的参数值
求函数值:用奇偶性将待求值转化为已知区间上的函数值求解
技巧点拨
1.设f(x)-x2=g(x),x∈R,若函数f(x)为偶函数,则g(x)的解析式可以为 ( )
A.g(x)=x3 B.g(x)=cos x
C.g(x)=1+x D.g(x)=xex
B
f(x)=x2+g(x)
f(x)为偶函数
(-x)2+g(-x)=x2+g(x)
g(-x)=g(x)
g(x)为偶函数
过关检测
2.设函数f(x)=,若f(x)是奇函数,则g(3)的值是 ( )
A.1 B.3 C.-3 D.-1
C
f(x)是奇函数
f(-3)=-f(3)
f(x)=
log2(1+3)=-(g(3)+1)
g(3)=-3
过关检测
3.若关于x的函数f(x)=(t≠0)的最大值为a,最小值为b,且a+b=2,则t=________.
f(x)==
设g(x)=
g(x)为奇函数
g(x)max+g(x)min=0
g(x)max=a-t
g(x)min=b-t
a+b-2t=0
a+b=2
t=1
1
过关检测
题型
三
函数的周期性
例5 设定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[0,2)时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2019)=________.
f(x+2)=f(x)
当x∈[0,2)时,f(x)=2x-x2
f(x)的周期T=2
f(0)=0,f(1)=1
f(0)=f(2)=f(4)=…=f(2 018)=0
f(1)=f(3)=f(5)=…=f(2 019)=1
f(0)+f(1)+f(2)+…+f(2019)=1010
1010
常考题型
函数周期性有关问题的求解策略
(1)求解与函数的周期性有关的问题,应根据题目特征及周期定义,求出函数的周期.
(2)周期函数的图象具有周期性,如果发现一个函数的图象具有两个对称性(注意:对称中心在平行于x轴的直线上,对称轴平行于y轴),那么这个函数一定具有周期性.
技巧点拨
1.已知函数f(x)的定义域为R,当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=-f(x);当x>时,,则f(6)等于 ( )
A.-2 B.-1 C.0 D.2
D
当x>时,
周期为1
f(6)=f(1)=-f(-1)=-[(-1)3-1]=2
过关检测
题型
四
函数性质的综合应用
考法(一) 单调性与奇偶性综合
例6 (石家庄质检)已知f(x)为奇函数,且当x>0时,f(x)单调递增,f(1)=0,若f(x-1)>0,则x的取值范围为( )
A.{x|0<x<1或x>2} B.{x|x<0或x>2}
C.{x|x<0或x>3} D.{x|x<-1或x>1}
常考题型
例6 (石家庄质检)已知f(x)为奇函数,且当x>0时,f(x)单调递增,f(1)=0,若f(x-1)>0,则x的取值范围为 ( )
A.{x|0<x<1或x>2} B.{x|x<0或x>2}
C.{x|x<0或x>3}
D.{x|x<-1或x>1}
f(x)的示意图
A
f(x-1)>0
-1<x-1<0或x-1>1
0<x<1或x>2
f(x)为奇函数
f(-1)=-f(1)=0
f(x)在(0,+∞)上单调递增
常考题型
考法(二) 奇偶性与周期性综合
例7 (赣州月考)定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为 ( )
A.(-∞,-3) B.(3,+∞)
C.(-∞,-1) D.(1,+∞)
题型
四
函数性质的综合应用
常考题型
例7 (2019·赣州月考)定义在R上的偶函数f(x)满足f(x+3)=f(x).若f(2)>1,f(7)=a,则实数a的取值范围为 ( )
A.(-∞,-3)
B.(3,+∞)
C.(-∞,-1)
D.(1,+∞)
D
f(x+3)=f(x)
f(x)是定义在R上的以3为周期的函数
f(7)=f(7-9)=f(-2)
函数f(x)是偶函数
f(-2)=f(2)
f(7)=f(2)>1
a>1
常考题型
考法(三) 单调性、奇偶性与周期性综合
例8 (达州模拟)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[-1,0]上单调递减,设a=f(-2.8),b=f(-1.6), c=f(0.5),则a,b,c的大小关系是 ( )
A.a>b>c B.c>a>b
C.b>c>a D.a>c>b
题型
四
函数性质的综合应用
常考题型
例8 (达州模拟)定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[-1,0]上单调递减,设a=f(-2.8),b=f(-1.6), c=f(0.5),则a,b,c的大小关系是 ( )
A.a>b>c
B.c>a>b
C.b>c>a
D.a>c>b
D
f(x+2)=f(x)
函数的周期为2
a=f(-2.8)=f(-0.8)
b=f(-1.6)=f(0.4)=f(-0.4)
c=f(0.5)=f(-0.5)
函数f(x)在 [-1,0]上单调递减
a>c>b
常考题型
考法(一) 已知函数单调递增且为奇函数,求自变量范围,有时也比较大小
常利用奇、偶函数图象的对称性;
考法(二)已知f(x)是周期函数且为偶函数,求函数值的范围
常利用奇偶性及周期性进行转换,将所求函数值的自变量转化到已知解析式的函数定义域内求解;
考法(三)函数周期性、奇偶性与单调性结合
解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.
技巧点拨
1.已知f(x)是定义在R上的偶函数,且f(x+1)=-f(x),若f(x)在[-1,0]上单调递减,则f(x)在[1,3]上是 ( )
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
D
f(x+1)=-f(x)
f(x+2)=-f(x+1)=f(x)
f(x)的周期是2
f(x)在定义域R上是偶函数
在[-1,0]上是减函数
f(x)在[0,1]上是增函数
f(x)在[1,2]上是减函数在[2,3]上是增函数
f(x)在[1,3]上是先减后增的函数
过关检测
2.(2018·全国卷Ⅱ)已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x).若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)= ( )
A.-50 B.0
C.2 D.50
f(x)是奇函数
f(1-x)=-f(x-1)
f(1-x)=f(1+x)
-f(x-1)=f(x+1)
f(x+2)=-f(x)
f(x+4)=-f(x+2)=f(x)
f(1-x)=f(1+x)
f(x)的图象关于直线x=1对称
f(2)=f(0)=0
f(-2)=0
f(1)=2
f(-1)=-2
f(1)+f(2)+f(3)+f(4)=f(1)+f(2)+f(-1)+f(0)=0
C
f(1)+f(2)+f(3)+f(4)+…+f(49)+f(50)=0×12+f(49)+f(50)=f(1)+f(2) =2
周期为4
过关检测
3.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f(-),则a的取值范围是________.
f(x)在(0,+∞)上单调递减,f(- )=f()
f(2|a-1|)>f(-)
f(2|a-1|)>f()
2|a-1|< =
|a-1|<
过关检测
再见
同课章节目录
