人教A版(2019)数学必修第一册期末复习: 集合重难点剖析 课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册期末复习: 集合重难点剖析 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 904.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
集合重难点剖析
期 末
复 习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
元素的三个特性
元素与集合的关系
集合的表示方法
确定性
无序性
互异性
属于,记为∈
不属于,记为
列举法
描述法
图示法
集合的
相关概念
此性质常用于题目中
对参数的取舍
核心考点
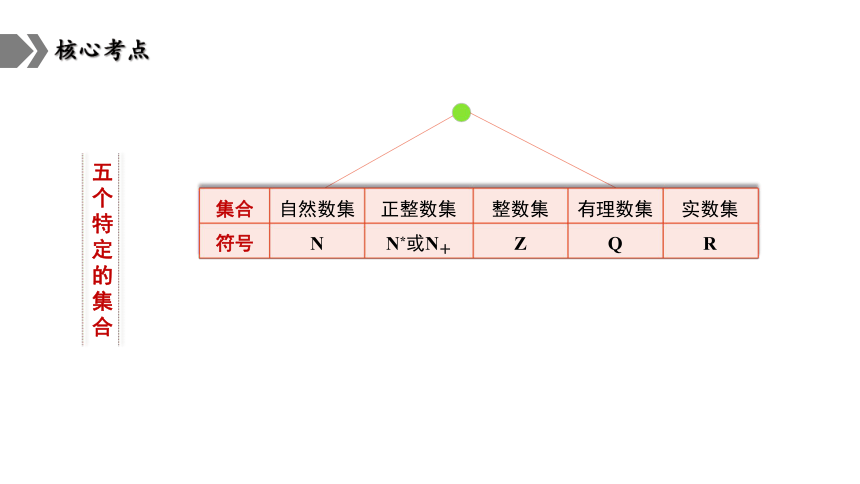
集合 自然数集 正整数集 整数集 有理数集 实数集
符号 N N*或N+ Z Q R
五
个
特
定
的
集
合
核心考点
集
合
间
的
基
本
关
系
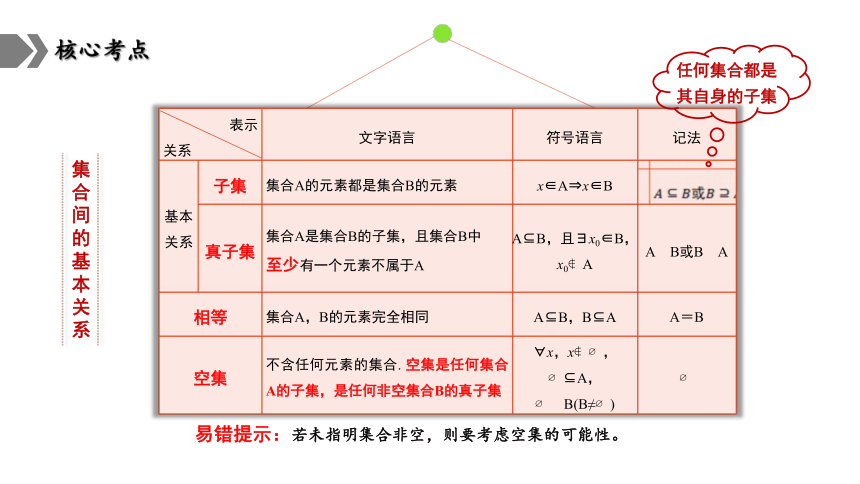
表示 关系 文字语言 符号语言 记法
基本关系 子集 集合A的元素都是集合B的元素 x∈A x∈B 或
真子集 集合A是集合B的子集,且集合B中 至少有一个元素不属于A A B,且 x0∈B,x0 A A B或B A
相等 集合A,B的元素完全相同 A B,B A A=B
空集 不含任何元素的集合. 空集是任何集合A的子集,是任何非空集合B的真子集 x,x , A, B(B≠ )
任何集合都是其自身的子集
易错提示:若未指明集合非空,则要考虑空集的可能性。
核心考点
集
合
的
基
本
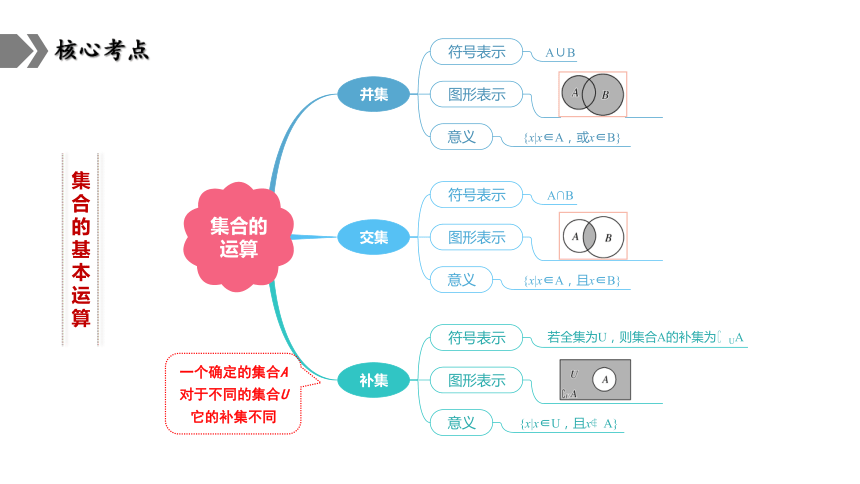
运算
并集
交集
补集
符号表示
A∪B
图形表示
意义
{x|x∈A,或x∈B}
符号表示
A∩B
意义
{x|x∈A,且x∈B}
符号表示
若全集为U,则集合A的补集为 UA
意义
{x|x∈U,且x A}
图形表示
图形表示
集合的
运算
一个确定的集合A
对于不同的集合U
它的补集不同
核心考点
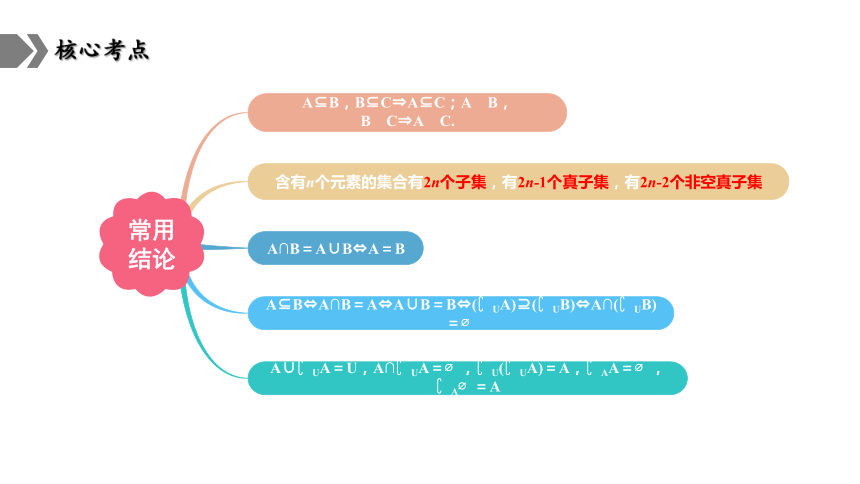
常用
结论
A B,B C A C;A B,B C A C.
含有n个元素的集合有2n个子集,有2n-1个真子集,有2n-2个非空真子集
A∩B=A∪B A=B
A B A∩B=A A∪B=B ( UA) ( UB) A∩( UB)=
A∪ UA=U,A∩ UA= , U( UA)=A, AA= , A =A
核心考点
1.已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是 ( )
A.-3∈A B.3 B
C.A∩B=B D.A∪B=B
C
A={y|y≥-1},
B={x|x≥2}
故A∩B={x|x≥2}=B.
过关检测
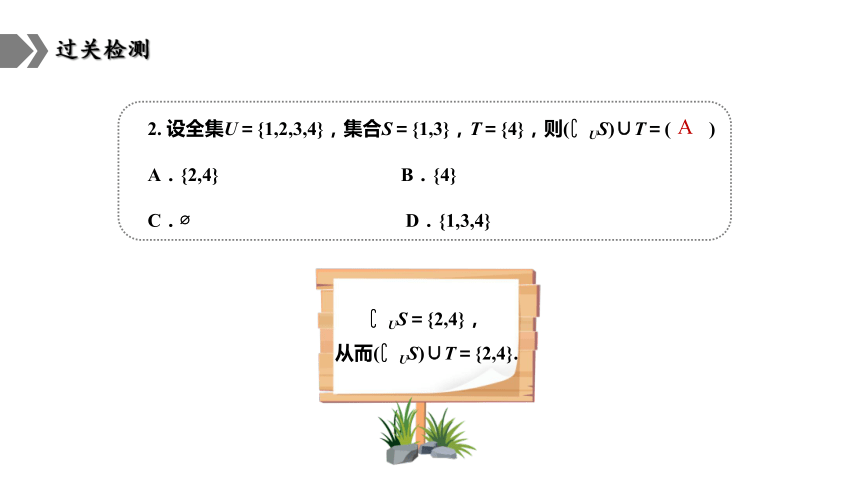
2. 设全集U={1,2,3,4},集合S={1,3},T={4},则( US)∪T=( )
A.{2,4} B.{4}
C. D.{1,3,4}
A
US={2,4},
从而( US)∪T={2,4}.
过关检测
3. 集合{-1,0,1}共有________个子集.
8
因为集合有3个元素,
所以集合共有23=8个子集.
过关检测
题型一
集合的含义及表示
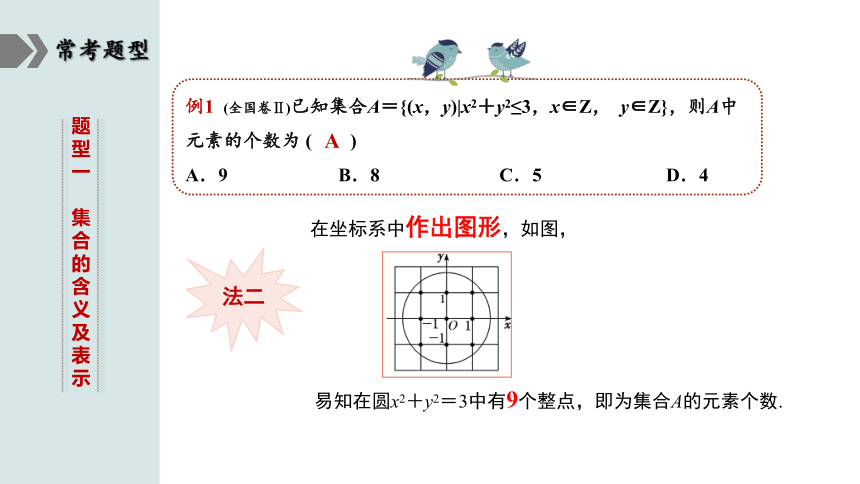
例1 (全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z, y∈Z},则A中元素的个数为 ( )
A.9 B.8 C.5 D.4
常考题型
将满足x2+y2≤3的整数x,y全部列举出来,即
(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共9个.
法一
A
题型一
集合的含义及表示
例1 (全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z, y∈Z},则A中元素的个数为 ( )
A.9 B.8 C.5 D.4
常考题型
法二
A
在坐标系中作出图形,如图,
易知在圆x2+y2=3中有9个整点,即为集合A的元素个数.
1.设a,b∈R,集合{1,a+b,a}=,则b-a=( )
A.1 B.-1 C.2 D.-2
a≠0
a≠0
a+b=0
=-1
a=-1,b=1
b-a=2
C
过关检测
2.已知集合A={x∈N|1<x<log2k},若集合A中至少有3个元素,则k的取值范围为 ( )
A.(8,+∞) B.[8,+∞) C.(16,+∞) D.[16,+∞)
集合A中至少有3个元素
log2k>4
k>24=16
C
过关检测
描述法的运用
互异性的运用
搞清楚集合中代表元素的含义
看元素的限制条件
明白集合类型(数集、点集还是其他)
含有字母的集合,在求出字母值后,
要检验元素是否满足互异性
特别注意
与元素有关问题的求解策略
技巧点拨
题型二
集合的基本关系
例2 设P={y|y=-x2+1,x∈R},Q={y|y=2x,x∈R},则( )
A.P Q B.Q P C. RP Q D.Q RP
注意集合的
代表元素
常考题型
P={y|y=-x2+1,x∈R}={y|y≤1}
Q={y|y=2x,x∈R}={y|y>0}
RP={y|y>1}
RP Q
C
例3 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为__________.
题型二
集合的基本关系
常考题型
B=
B≠
2m-1<m+1
m<2
2m-1≥m+1
m+1≥-2
2m-1≤5
2≤m≤3
m的取值范围为(-∞,3]
(-∞,3]
B A
变式发散
常考题型
变式1 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为__________.
(-∞,3]
B=
B≠
2m-1<m+1
m<2
2m-1≥m+1
m+1≥-2
2m-1<5
2≤m≤3
m的取值范围为(-∞,3]
BA
2m-1≥m+1
m+1>-2
2m-1 ≤ 5
或
变式发散
常考题型
变式2 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若A B,则实数m的取值范围为__________.
m+1≤-2
2m-1≥5
m≤ -3
m为
A B
m≥3
2种方法
1个关键
化简集合,从表达式中寻找关系
用列举法(或图示法等)表示集合,从元素(或图形)中寻找关系
看它们是否具有包含关系
判定集合间
基本关系
技巧点拨
元素是一一列举的
转化为解方程(组)求解
集合表示的是不等式的解集时
转化为不等式(组)求解
注意集合中元素的互异性
需注意端点值能否取到
根据集合间的
关系求参数的
方法
技巧点拨
1.设M为非空的数集,M {1,2,3},且M中至少含有一个奇数元素,则这样的集合M共有 ( )
A.6个 B.5个 C.4个 D.3个
M={1},{3},{1,2},{1,3},{2,3},{1,2,3}
A
过关检测
2.已知集合A={1,2},B={x|x2+mx+1=0,x∈R},若B A,则实数 m 的取值范围为________.
Δ=m2-4<0
-2<m<2
12+m+1=0
m=-2
B={1}
B A
B=
1∈B
2∈B
22+2m+1=0
m=
B=
m的取值范围为[-2,2)
不符合题意
[-2,2)
过关检测
题型三
集合的基本运算
例4 (天津高考)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C= ( )
A.{-1,1} B.{0,1}
C.{-1,0,1} D.{2,3,4}
常考题型
A={1,2,3,4}
B={-1,0,2,3}
A∪B={-1,0,1,2,3,4}
C={x∈R|-1≤x<2}
(A∪B)∩C={-1,0,1}
C
例5 已知集合A={x|x2-x-12>0},B={x|x≥m}.若A∩B={x|x>4},则实数 m 的取值范围是( )
A.(-4,3) B.[-3,4]
C.(-3,4) D.(-∞,4]
题型三
集合的基本运算
常考题型
A={x|x<-3或x>4}
A∩B={x|x>4}
-3≤m≤4
-3
4
A={x|x2-x-12>0}
B
用列举法表示的集合
用不等式表示的集合
用数轴求解
通过列举元素来计算
借助Venn图来计算
集合的运算技巧
技巧点拨
交集元素仔细找,属于A且属于B;
并集元素勿遗漏,切记重复仅取一;
全集U是大范围,去掉U中a元素,剩余元素成补集.
集合的交、并、补运算口诀
技巧点拨
1.集合M={y|y=-x2,x∈R},N={x|x2+y2=2,x∈R},则M∩N= ( )
A.{(-1,-1),(1,-1)} B.{-1}
C.[-1,0] D.[-,0]
M=(-∞,0]
N=[- , ]
M∩N=[- ,0]
D
过关检测
2.若集合A={x|-1<x<1,x∈R},B={x|y=,x∈R},则A∪B= ( )
A.[0,1) B.(-1,+∞)
C.(-1,1)∪[2,+∞) D.
A∪B={x|-1<x<1或x≥2}
B={x|y=
B={x|x≥2}
C
过关检测
3.已知集合A={x|x2-x-2>0},则 RA=( )
A.{x|-1<x<2} B.{x|-1≤x≤2}
C.{x|x<-1}∪{x|x>2} D.{x|x≤-1}∪{x|x≥2}
B
RA={x|-1≤x≤2}
x2-x-2>0
x>2或x<-1
A={x|x>2或x<-1}
过关检测
题型四
集合的新定义问题
例6 如图所示的Venn图中,A,B是两个非空集合,定义集合A B为阴影部分表示的集合.若x,y∈R,A={x|y=},B={y|y=3x,x>0},则A B为( )
A.{x|0<x<2} B.{x|1<x≤2}
C.{x|0≤x≤1或x≥2} D.{x|0≤x≤1或x>2}
常考题型
A={x|0≤x≤2}
B={y|y>1}
A∪B={x|x≥0}
A∩B={x|1<x≤2}
A B= A∪B(A∩B)={x|0≤x≤1或x>2}.
D
例7 给定集合A,若对于任意a,b∈A,有a+b∈A,且a-b∈A,则称集合A为闭集合,给出如下三个结论:
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合.
其中正确结论的序号是________.
题型四
集合的新定义问题
常考题型
①中,-4+(-2)=-6 A,所以①不正确;
②中,设n1,n2∈A,n1=3k1,n2=3k2,k1,k2∈Z,则n1+n2∈A,n1-n2∈A,所以②正确;
③中,令A1={n|n=3k,k∈Z},A2={n|n=k,k∈Z},则A1,A2为闭集合,但3k+k (A1∪A2),故A1∪A2不是闭集合,所以③不正确.
②
紧扣新定义
弄清新定义问题的本质
灵活应用到解题过程中
用好集合的性质
集合元素的性质
集合计算的性质
关键
突破口
解决新定义问题
的两个策略
技巧点拨
1.设P和Q是两个集合,定义集合P-Q={x|x∈P,且x Q},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q=( )
A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
B
P-Q={x|0<x≤1}
log2x<1
0<x<2
P={x|0<x<2}
|x-2|<1
1<x<3
Q={x|1<x<3}
过关检测
再见
集合重难点剖析
期 末
复 习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
元素的三个特性
元素与集合的关系
集合的表示方法
确定性
无序性
互异性
属于,记为∈
不属于,记为
列举法
描述法
图示法
集合的
相关概念
此性质常用于题目中
对参数的取舍
核心考点
集合 自然数集 正整数集 整数集 有理数集 实数集
符号 N N*或N+ Z Q R
五
个
特
定
的
集
合
核心考点
集
合
间
的
基
本
关
系
表示 关系 文字语言 符号语言 记法
基本关系 子集 集合A的元素都是集合B的元素 x∈A x∈B 或
真子集 集合A是集合B的子集,且集合B中 至少有一个元素不属于A A B,且 x0∈B,x0 A A B或B A
相等 集合A,B的元素完全相同 A B,B A A=B
空集 不含任何元素的集合. 空集是任何集合A的子集,是任何非空集合B的真子集 x,x , A, B(B≠ )
任何集合都是其自身的子集
易错提示:若未指明集合非空,则要考虑空集的可能性。
核心考点
集
合
的
基
本
运算
并集
交集
补集
符号表示
A∪B
图形表示
意义
{x|x∈A,或x∈B}
符号表示
A∩B
意义
{x|x∈A,且x∈B}
符号表示
若全集为U,则集合A的补集为 UA
意义
{x|x∈U,且x A}
图形表示
图形表示
集合的
运算
一个确定的集合A
对于不同的集合U
它的补集不同
核心考点
常用
结论
A B,B C A C;A B,B C A C.
含有n个元素的集合有2n个子集,有2n-1个真子集,有2n-2个非空真子集
A∩B=A∪B A=B
A B A∩B=A A∪B=B ( UA) ( UB) A∩( UB)=
A∪ UA=U,A∩ UA= , U( UA)=A, AA= , A =A
核心考点
1.已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是 ( )
A.-3∈A B.3 B
C.A∩B=B D.A∪B=B
C
A={y|y≥-1},
B={x|x≥2}
故A∩B={x|x≥2}=B.
过关检测
2. 设全集U={1,2,3,4},集合S={1,3},T={4},则( US)∪T=( )
A.{2,4} B.{4}
C. D.{1,3,4}
A
US={2,4},
从而( US)∪T={2,4}.
过关检测
3. 集合{-1,0,1}共有________个子集.
8
因为集合有3个元素,
所以集合共有23=8个子集.
过关检测
题型一
集合的含义及表示
例1 (全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z, y∈Z},则A中元素的个数为 ( )
A.9 B.8 C.5 D.4
常考题型
将满足x2+y2≤3的整数x,y全部列举出来,即
(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共9个.
法一
A
题型一
集合的含义及表示
例1 (全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z, y∈Z},则A中元素的个数为 ( )
A.9 B.8 C.5 D.4
常考题型
法二
A
在坐标系中作出图形,如图,
易知在圆x2+y2=3中有9个整点,即为集合A的元素个数.
1.设a,b∈R,集合{1,a+b,a}=,则b-a=( )
A.1 B.-1 C.2 D.-2
a≠0
a≠0
a+b=0
=-1
a=-1,b=1
b-a=2
C
过关检测
2.已知集合A={x∈N|1<x<log2k},若集合A中至少有3个元素,则k的取值范围为 ( )
A.(8,+∞) B.[8,+∞) C.(16,+∞) D.[16,+∞)
集合A中至少有3个元素
log2k>4
k>24=16
C
过关检测
描述法的运用
互异性的运用
搞清楚集合中代表元素的含义
看元素的限制条件
明白集合类型(数集、点集还是其他)
含有字母的集合,在求出字母值后,
要检验元素是否满足互异性
特别注意
与元素有关问题的求解策略
技巧点拨
题型二
集合的基本关系
例2 设P={y|y=-x2+1,x∈R},Q={y|y=2x,x∈R},则( )
A.P Q B.Q P C. RP Q D.Q RP
注意集合的
代表元素
常考题型
P={y|y=-x2+1,x∈R}={y|y≤1}
Q={y|y=2x,x∈R}={y|y>0}
RP={y|y>1}
RP Q
C
例3 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为__________.
题型二
集合的基本关系
常考题型
B=
B≠
2m-1<m+1
m<2
2m-1≥m+1
m+1≥-2
2m-1≤5
2≤m≤3
m的取值范围为(-∞,3]
(-∞,3]
B A
变式发散
常考题型
变式1 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若B A,则实数m的取值范围为__________.
(-∞,3]
B=
B≠
2m-1<m+1
m<2
2m-1≥m+1
m+1≥-2
2m-1<5
2≤m≤3
m的取值范围为(-∞,3]
BA
2m-1≥m+1
m+1>-2
2m-1 ≤ 5
或
变式发散
常考题型
变式2 已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},若A B,则实数m的取值范围为__________.
m+1≤-2
2m-1≥5
m≤ -3
m为
A B
m≥3
2种方法
1个关键
化简集合,从表达式中寻找关系
用列举法(或图示法等)表示集合,从元素(或图形)中寻找关系
看它们是否具有包含关系
判定集合间
基本关系
技巧点拨
元素是一一列举的
转化为解方程(组)求解
集合表示的是不等式的解集时
转化为不等式(组)求解
注意集合中元素的互异性
需注意端点值能否取到
根据集合间的
关系求参数的
方法
技巧点拨
1.设M为非空的数集,M {1,2,3},且M中至少含有一个奇数元素,则这样的集合M共有 ( )
A.6个 B.5个 C.4个 D.3个
M={1},{3},{1,2},{1,3},{2,3},{1,2,3}
A
过关检测
2.已知集合A={1,2},B={x|x2+mx+1=0,x∈R},若B A,则实数 m 的取值范围为________.
Δ=m2-4<0
-2<m<2
12+m+1=0
m=-2
B={1}
B A
B=
1∈B
2∈B
22+2m+1=0
m=
B=
m的取值范围为[-2,2)
不符合题意
[-2,2)
过关检测
题型三
集合的基本运算
例4 (天津高考)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C= ( )
A.{-1,1} B.{0,1}
C.{-1,0,1} D.{2,3,4}
常考题型
A={1,2,3,4}
B={-1,0,2,3}
A∪B={-1,0,1,2,3,4}
C={x∈R|-1≤x<2}
(A∪B)∩C={-1,0,1}
C
例5 已知集合A={x|x2-x-12>0},B={x|x≥m}.若A∩B={x|x>4},则实数 m 的取值范围是( )
A.(-4,3) B.[-3,4]
C.(-3,4) D.(-∞,4]
题型三
集合的基本运算
常考题型
A={x|x<-3或x>4}
A∩B={x|x>4}
-3≤m≤4
-3
4
A={x|x2-x-12>0}
B
用列举法表示的集合
用不等式表示的集合
用数轴求解
通过列举元素来计算
借助Venn图来计算
集合的运算技巧
技巧点拨
交集元素仔细找,属于A且属于B;
并集元素勿遗漏,切记重复仅取一;
全集U是大范围,去掉U中a元素,剩余元素成补集.
集合的交、并、补运算口诀
技巧点拨
1.集合M={y|y=-x2,x∈R},N={x|x2+y2=2,x∈R},则M∩N= ( )
A.{(-1,-1),(1,-1)} B.{-1}
C.[-1,0] D.[-,0]
M=(-∞,0]
N=[- , ]
M∩N=[- ,0]
D
过关检测
2.若集合A={x|-1<x<1,x∈R},B={x|y=,x∈R},则A∪B= ( )
A.[0,1) B.(-1,+∞)
C.(-1,1)∪[2,+∞) D.
A∪B={x|-1<x<1或x≥2}
B={x|y=
B={x|x≥2}
C
过关检测
3.已知集合A={x|x2-x-2>0},则 RA=( )
A.{x|-1<x<2} B.{x|-1≤x≤2}
C.{x|x<-1}∪{x|x>2} D.{x|x≤-1}∪{x|x≥2}
B
RA={x|-1≤x≤2}
x2-x-2>0
x>2或x<-1
A={x|x>2或x<-1}
过关检测
题型四
集合的新定义问题
例6 如图所示的Venn图中,A,B是两个非空集合,定义集合A B为阴影部分表示的集合.若x,y∈R,A={x|y=},B={y|y=3x,x>0},则A B为( )
A.{x|0<x<2} B.{x|1<x≤2}
C.{x|0≤x≤1或x≥2} D.{x|0≤x≤1或x>2}
常考题型
A={x|0≤x≤2}
B={y|y>1}
A∪B={x|x≥0}
A∩B={x|1<x≤2}
A B= A∪B(A∩B)={x|0≤x≤1或x>2}.
D
例7 给定集合A,若对于任意a,b∈A,有a+b∈A,且a-b∈A,则称集合A为闭集合,给出如下三个结论:
①集合A={-4,-2,0,2,4}为闭集合;
②集合A={n|n=3k,k∈Z}为闭集合;
③若集合A1,A2为闭集合,则A1∪A2为闭集合.
其中正确结论的序号是________.
题型四
集合的新定义问题
常考题型
①中,-4+(-2)=-6 A,所以①不正确;
②中,设n1,n2∈A,n1=3k1,n2=3k2,k1,k2∈Z,则n1+n2∈A,n1-n2∈A,所以②正确;
③中,令A1={n|n=3k,k∈Z},A2={n|n=k,k∈Z},则A1,A2为闭集合,但3k+k (A1∪A2),故A1∪A2不是闭集合,所以③不正确.
②
紧扣新定义
弄清新定义问题的本质
灵活应用到解题过程中
用好集合的性质
集合元素的性质
集合计算的性质
关键
突破口
解决新定义问题
的两个策略
技巧点拨
1.设P和Q是两个集合,定义集合P-Q={x|x∈P,且x Q},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q=( )
A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
B
P-Q={x|0<x≤1}
log2x<1
0<x<2
P={x|0<x<2}
|x-2|<1
1<x<3
Q={x|1<x<3}
过关检测
再见
同课章节目录
