人教A版(2019)数学必修第一册期末复习:同角三角函数的基本关系与诱导公式 课件(共35张PPT)
文档属性
| 名称 | 人教A版(2019)数学必修第一册期末复习:同角三角函数的基本关系与诱导公式 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览




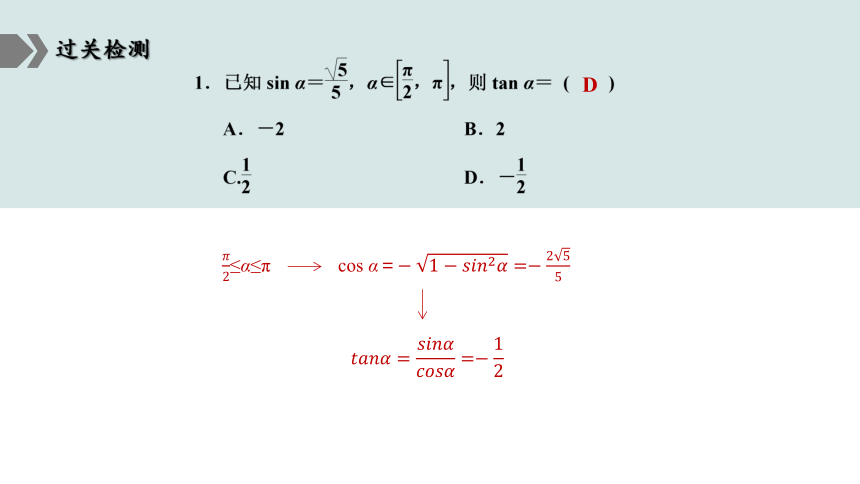
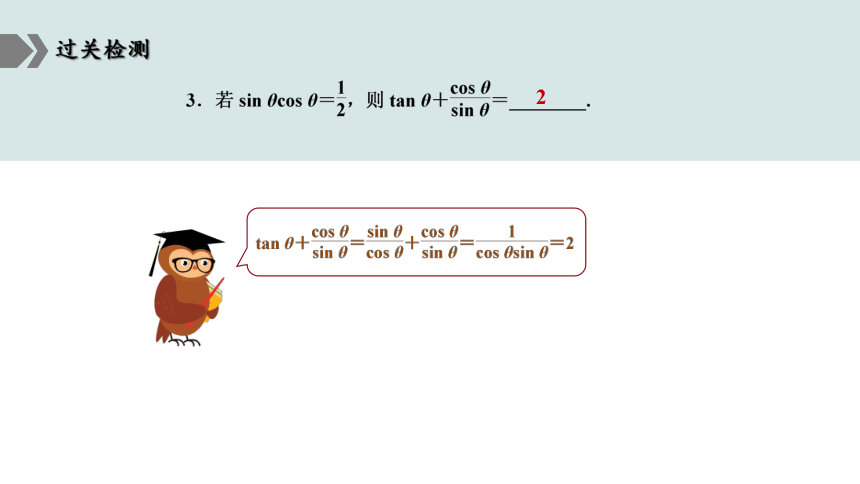

文档简介
(共35张PPT)
同角三角函数的基本关系与诱导公式
期末
复习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
1
同角三角函数的基本关系
(1)
平方关系
sin2α+cos2α=1
(2)
商数关系
作用:实现同角的正弦值与余弦值之间的转化,利用该公式求值,要注意确定角的终边所在的象限,从而判断三角函数值的符号.
作用:切化弦,弦切互化.
核心考点
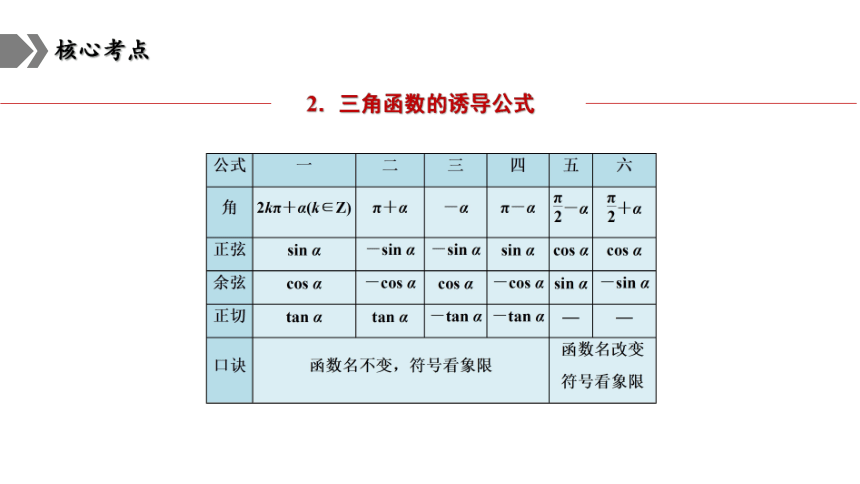
2.三角函数的诱导公式
核心考点
同角三角函数的基本关系式的几种变形
核心考点
常用结论
诱导公式可记为:奇变偶不变,符号看象限.
“奇”“偶”指的是“k·+α(k∈Z)”中的k是奇数还是偶数.
“变”与“不变”是指函数名称的变化,若k是奇数,则正、余弦互变;若k为偶数,则函数名称不变.
“符号看象限”指的是在“k·+α(k∈Z)”中,将α看成锐角时,“k·+α(k∈Z)”的终边所在的象限.
核心考点
常用结论
≤α≤π
cos α=
D
过关检测
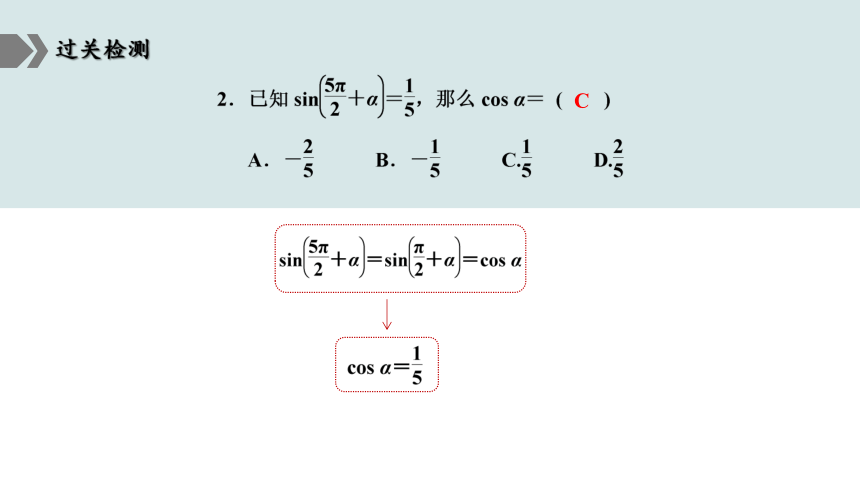
C
过关检测
2
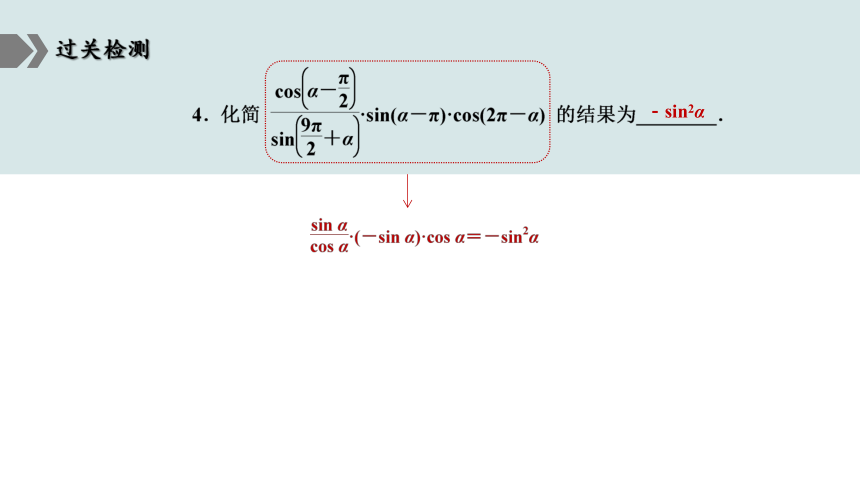
过关检测
-sin2α
过关检测
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
考法(一) 公式的直接应用
设角α终边上一点P(k,y)(k<0,y>0)
|OP|=1
sin α=
B
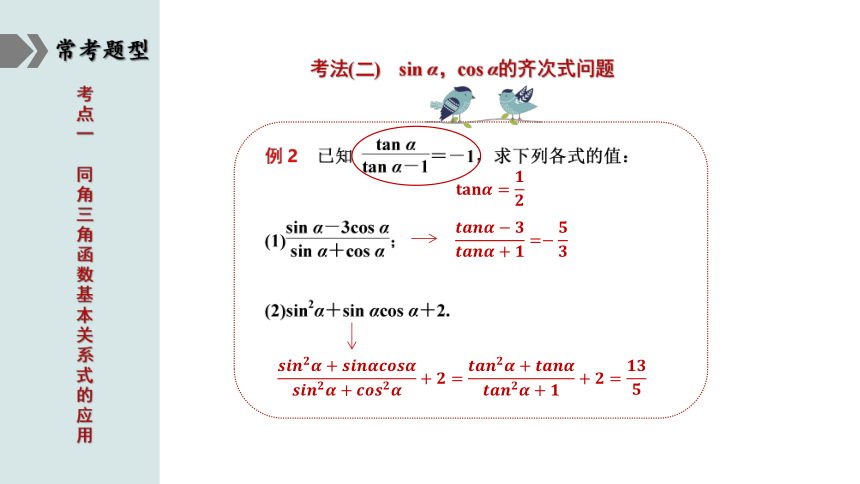
常考题型
考法(二) sin α,cos α的齐次式问题
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
常考题型
考法(三) “sin α±cos α,sin αcos α”之间的关系的应用
例3 已知x∈(-π,0),sin x+cos x=.
(1)求sin x-cos x的值;
(2)求的值.
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
常考题型
例3 已知x∈(-π,0),sin x+cos x=.
(1)求sin x-cos x的值;
sin x+cos x=
sin2x+2sin xcos x+cos2x=
2sin xcos x=-
(sin x-cos x)2=1-2sin xcos x=
x∈(-π,0)知sin x<0
cos x>0
sin x-cos x<0
sin x-cos x=
sin x+cos x>0
常考题型
例3 已知x∈(-π,0),sin x+cos x=.
(2)求的值.
常考题型
考法(一)是公式的直接应用,即已知sin α,cos α,tan α中的一个求另外两个
解决此类问题时,直接套用公式sin2α+cos2α=1及tan α=即可,但要注意α的范围,即三角函数值的符号.
考法(二)的分式中分子与分母是关于sin α,cos α的齐次式
往往转化为关于tan α的式子求解.
考法(三)是考查sin α±cos α与sin αcos α的关系
对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二
技巧点拨
利用sin2α+cos2α=1可实现正、余弦的互化,开方时要根据角α所在象限确定符号;
利用=tan α可以实现角α的弦切互化;
利用(sin α±cos α)2=1±2sin αcos α的关系可实现和积转化.
技巧点拨
sin α<0,cos α<0
过关检测
B
1+2sin xcos x=1-
2sin xcos x=- <0
x为钝角
sin x-cos x=
sin x= ,cos x=
tan x=
sin x+cos x=
D
过关检测
过关检测
考
点
二
诱
导
公
式
的
应
用
常考题型
0
考
点
二
诱
导
公
式
的
应
用
常考题型
1.利用诱导公式解题的一般思路
(1)化绝对值大的角为锐角.
(2)角中含有加减的整数倍时,用公式去掉的整数倍.
技巧点拨
解题技法
2.常见的互余和互补的角
解题技法
技巧点拨
2
过关检测
5x2-7x-6=0的根为x1=2,x2=
sin α=
cos α=
tan α=
α是第三象限角
过关检测
B
过关检测
考
点
三
诱
导
公
式
与
同
角
关
系
的
综
合
应
用
常考题型
综上f(x)=sin2x
常考题型
常考题型
求解诱导公式与同角关系综合问题的基本思路和化简要求
化简要求
基本思路
①化简过程是恒等变换;
②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值
①分析结构特点,选择恰当公式;
②利用公式化成单角三角函数;
③整理得最简形式
技巧点拨
-2tan α+3sin β+5=0
tan α-6sin β-1=0
tan α=3
α为锐角
sin α=
C
过关检测
tan(π-α)=-
tan α=
过关检测
过关检测
再见
同角三角函数的基本关系与诱导公式
期末
复习
核心
考点
常考
题型
跟踪
检测
>>
>>
目
录
1
同角三角函数的基本关系
(1)
平方关系
sin2α+cos2α=1
(2)
商数关系
作用:实现同角的正弦值与余弦值之间的转化,利用该公式求值,要注意确定角的终边所在的象限,从而判断三角函数值的符号.
作用:切化弦,弦切互化.
核心考点
2.三角函数的诱导公式
核心考点
同角三角函数的基本关系式的几种变形
核心考点
常用结论
诱导公式可记为:奇变偶不变,符号看象限.
“奇”“偶”指的是“k·+α(k∈Z)”中的k是奇数还是偶数.
“变”与“不变”是指函数名称的变化,若k是奇数,则正、余弦互变;若k为偶数,则函数名称不变.
“符号看象限”指的是在“k·+α(k∈Z)”中,将α看成锐角时,“k·+α(k∈Z)”的终边所在的象限.
核心考点
常用结论
≤α≤π
cos α=
D
过关检测
C
过关检测
2
过关检测
-sin2α
过关检测
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
考法(一) 公式的直接应用
设角α终边上一点P(k,y)(k<0,y>0)
|OP|=1
sin α=
B
常考题型
考法(二) sin α,cos α的齐次式问题
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
常考题型
考法(三) “sin α±cos α,sin αcos α”之间的关系的应用
例3 已知x∈(-π,0),sin x+cos x=.
(1)求sin x-cos x的值;
(2)求的值.
考
点
一
同
角
三
角
函
数
基
本
关
系
式
的
应
用
常考题型
例3 已知x∈(-π,0),sin x+cos x=.
(1)求sin x-cos x的值;
sin x+cos x=
sin2x+2sin xcos x+cos2x=
2sin xcos x=-
(sin x-cos x)2=1-2sin xcos x=
x∈(-π,0)知sin x<0
cos x>0
sin x-cos x<0
sin x-cos x=
sin x+cos x>0
常考题型
例3 已知x∈(-π,0),sin x+cos x=.
(2)求的值.
常考题型
考法(一)是公式的直接应用,即已知sin α,cos α,tan α中的一个求另外两个
解决此类问题时,直接套用公式sin2α+cos2α=1及tan α=即可,但要注意α的范围,即三角函数值的符号.
考法(二)的分式中分子与分母是关于sin α,cos α的齐次式
往往转化为关于tan α的式子求解.
考法(三)是考查sin α±cos α与sin αcos α的关系
对于sin α+cos α,sin α-cos α,sin αcos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二
技巧点拨
利用sin2α+cos2α=1可实现正、余弦的互化,开方时要根据角α所在象限确定符号;
利用=tan α可以实现角α的弦切互化;
利用(sin α±cos α)2=1±2sin αcos α的关系可实现和积转化.
技巧点拨
sin α<0,cos α<0
过关检测
B
1+2sin xcos x=1-
2sin xcos x=- <0
x为钝角
sin x-cos x=
sin x= ,cos x=
tan x=
sin x+cos x=
D
过关检测
过关检测
考
点
二
诱
导
公
式
的
应
用
常考题型
0
考
点
二
诱
导
公
式
的
应
用
常考题型
1.利用诱导公式解题的一般思路
(1)化绝对值大的角为锐角.
(2)角中含有加减的整数倍时,用公式去掉的整数倍.
技巧点拨
解题技法
2.常见的互余和互补的角
解题技法
技巧点拨
2
过关检测
5x2-7x-6=0的根为x1=2,x2=
sin α=
cos α=
tan α=
α是第三象限角
过关检测
B
过关检测
考
点
三
诱
导
公
式
与
同
角
关
系
的
综
合
应
用
常考题型
综上f(x)=sin2x
常考题型
常考题型
求解诱导公式与同角关系综合问题的基本思路和化简要求
化简要求
基本思路
①化简过程是恒等变换;
②结果要求项数尽可能少,次数尽可能低,结构尽可能简单,能求值的要求出值
①分析结构特点,选择恰当公式;
②利用公式化成单角三角函数;
③整理得最简形式
技巧点拨
-2tan α+3sin β+5=0
tan α-6sin β-1=0
tan α=3
α为锐角
sin α=
C
过关检测
tan(π-α)=-
tan α=
过关检测
过关检测
再见
同课章节目录
