人教A版(2019)数学选择性必修一册1.1.2空间向量的数量积运算 课时精练(含解析)
文档属性
| 名称 | 人教A版(2019)数学选择性必修一册1.1.2空间向量的数量积运算 课时精练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 117.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览


文档简介
1.1.2空间向量的数量积运算
一、常考题型
1.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b=-,则两直线的夹角为( )
A.30° B.60°
C.120° D.150°
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2
C.a2 D.a2
3.如图所示,已知空间四边形每条边和对角线长都为a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是( )
A.2· B.2·
C.2· D.2·
4.已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是( )
A.60° B.120°
C.30° D.90°
5.在正方体ABCD A1B1C1D1中,有下列命题:
①(++)2=32;
②·(-)=0;
③与的夹角为60°;
④正方体的体积为|··|.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
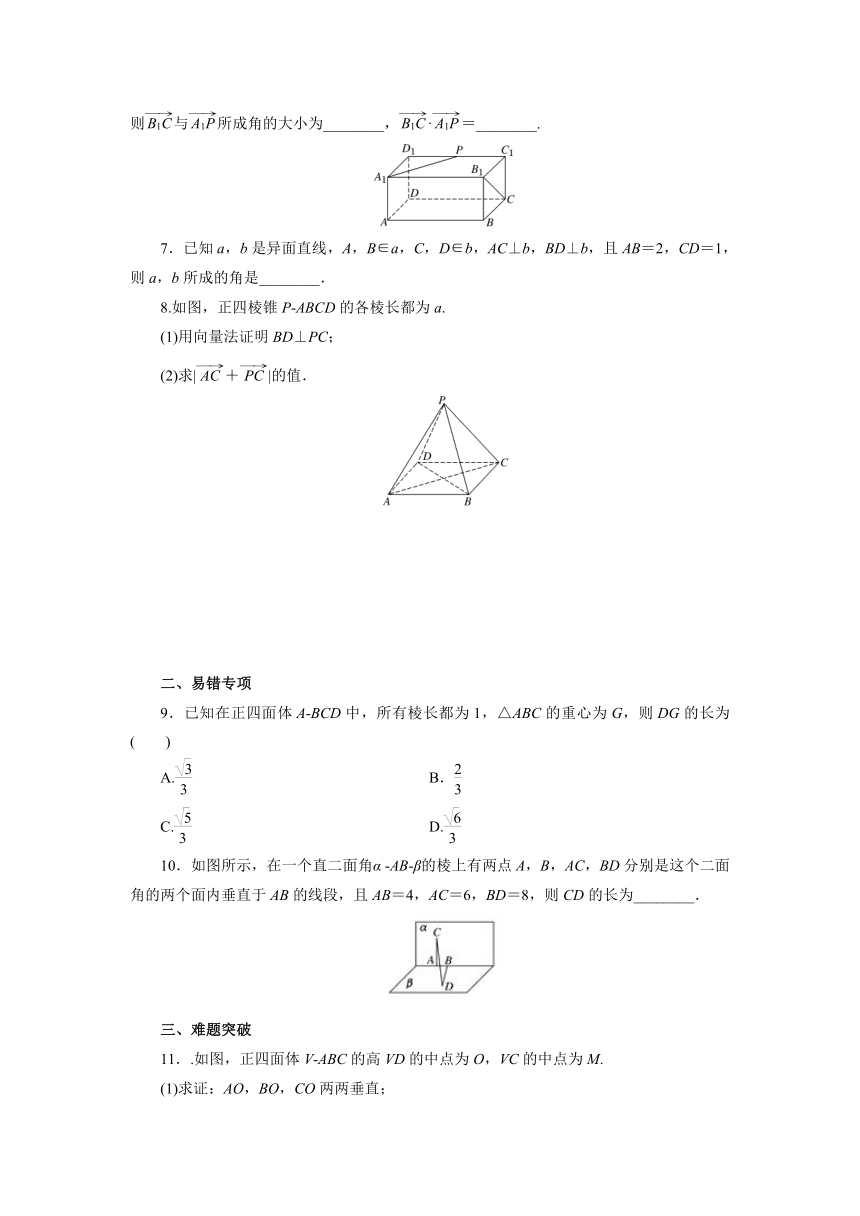
6.如图,在长方体ABCD A1B1C1D1中,设AD=AA1=1,AB=2,P是C1D1的中点,则与所成角的大小为________,·=________.
7.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
8.如图,正四棱锥P ABCD的各棱长都为a.
(1)用向量法证明BD⊥PC;
(2)求|+|的值.
二、易错专项
9.已知在正四面体A BCD中,所有棱长都为1,△ABC的重心为G,则DG的长为( )
A. B.
C. D.
10.如图所示,在一个直二面角α AB β的棱上有两点A,B,AC,BD分别是这个二面角的两个面内垂直于AB的线段,且AB=4,AC=6,BD=8,则CD的长为________.
三、难题突破
11..如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
参考答案
1.解析:选B 设向量a,b的夹角为θ,
则cos θ==-,所以θ=120°,
则两个方向向量对应的直线的夹角为180°-120°=60°.
2.解析:选C ·=(+)·
=(·+·)==a2.
3.解析:选B 2·=-2a2cos 60°=-a2,
2·=2·=2a2cos 60°=a2,
2·=·=-a2,
2·=·=-·=-a2,故选B.
4.解析:选B a·b=(e1+e2)·(e1-2e2)=e-e1·e2-2e=1-1×1×-2=-,
|a|=====,
|b|=====.
∴cos〈a,b〉===-.
∴〈a,b〉=120°.
5.解析:选B 如图所示,
(++)2=(++)2=2=32;
·(-)=·=0;
与的夹角是与夹角的补角,而与的夹角为60°,故与的夹角为120°;
正方体的体积为||||||.
综上可知,①②正确.
6.解析:法一:连接A1D,
则∠PA1D就是与所成角.连接PD,
在△PA1D中,易得PA1=DA1=PD=,
即△PA1D为等边三角形,从而∠PA1D=60°,
即与所成角的大小为60°.
因此·=××cos 60°=1.
法二:根据向量的线性运算可得·=(+)·=2=1.
由题意可得PA1=B1C=,则××cos〈,〉=1,
从而〈,〉=60°.
答案:60° 1
7.解析:=++,
∴·=·(++)=||2=1,
∴cos〈,〉==,
∴异面直线a,b所成角是60°.
答案:60°
8. 解:(1)证明:∵=+,
∴·=(+)·=·+·
=||||·cos 60°+||||cos 120°=a2-a2=0.
∴BD⊥PC.
(2)∵+=++,
∴|+|2=||2+||2+||2+2·+2·+2·
=a2+a2+a2+0+2a2cos 60°+2a2cos 60°=5a2,
∴|+|=a.
9.解析:选D 如图,连接AG并延长交BC于点M,连接DM,
∵G是△ABC的重心,∴AG=AM,
∴=,
=+=+=+(-)
=+
=(++),
而(++)2=+++2·+2·+2·
=1+1+1+2(cos 60°+cos 60°+cos 60°)=6,
∴||=.
10.解析:∵=++=-+,
∴=(-+)2
=++-2·+2·-2·
=16+36+64=116,
∴||=2.
答案:2
11.解:设=a, =b, =c,正四面体的棱长为1,
(1)证明:因为=(a+b+c),=(b+c-5a), =(a+c-5b), =(a+b-5c),
所以·=(b+c-5a)·(a+c-5b)
=(18a·b-9|a|2)
==0,
所以⊥,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
(2) 因为=+=-(a+b+c)+c=(-2a-2b+c),
所以||= =.
又||= =,
·=(-2a-2b+c)·(b+c-5a)=,
所以cos〈,〉==.
又〈,〉∈[0,π],所以〈,〉=.
一、常考题型
1.已知两异面直线的方向向量分别为a,b,且|a|=|b|=1,a·b=-,则两直线的夹角为( )
A.30° B.60°
C.120° D.150°
2.已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则·的值为( )
A.a2 B.a2
C.a2 D.a2
3.如图所示,已知空间四边形每条边和对角线长都为a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是( )
A.2· B.2·
C.2· D.2·
4.已知e1,e2是夹角为60°的两个单位向量,则a=e1+e2与b=e1-2e2的夹角是( )
A.60° B.120°
C.30° D.90°
5.在正方体ABCD A1B1C1D1中,有下列命题:
①(++)2=32;
②·(-)=0;
③与的夹角为60°;
④正方体的体积为|··|.
其中正确命题的个数是( )
A.1 B.2
C.3 D.4
6.如图,在长方体ABCD A1B1C1D1中,设AD=AA1=1,AB=2,P是C1D1的中点,则与所成角的大小为________,·=________.
7.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
8.如图,正四棱锥P ABCD的各棱长都为a.
(1)用向量法证明BD⊥PC;
(2)求|+|的值.
二、易错专项
9.已知在正四面体A BCD中,所有棱长都为1,△ABC的重心为G,则DG的长为( )
A. B.
C. D.
10.如图所示,在一个直二面角α AB β的棱上有两点A,B,AC,BD分别是这个二面角的两个面内垂直于AB的线段,且AB=4,AC=6,BD=8,则CD的长为________.
三、难题突破
11..如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
参考答案
1.解析:选B 设向量a,b的夹角为θ,
则cos θ==-,所以θ=120°,
则两个方向向量对应的直线的夹角为180°-120°=60°.
2.解析:选C ·=(+)·
=(·+·)==a2.
3.解析:选B 2·=-2a2cos 60°=-a2,
2·=2·=2a2cos 60°=a2,
2·=·=-a2,
2·=·=-·=-a2,故选B.
4.解析:选B a·b=(e1+e2)·(e1-2e2)=e-e1·e2-2e=1-1×1×-2=-,
|a|=====,
|b|=====.
∴cos〈a,b〉===-.
∴〈a,b〉=120°.
5.解析:选B 如图所示,
(++)2=(++)2=2=32;
·(-)=·=0;
与的夹角是与夹角的补角,而与的夹角为60°,故与的夹角为120°;
正方体的体积为||||||.
综上可知,①②正确.
6.解析:法一:连接A1D,
则∠PA1D就是与所成角.连接PD,
在△PA1D中,易得PA1=DA1=PD=,
即△PA1D为等边三角形,从而∠PA1D=60°,
即与所成角的大小为60°.
因此·=××cos 60°=1.
法二:根据向量的线性运算可得·=(+)·=2=1.
由题意可得PA1=B1C=,则××cos〈,〉=1,
从而〈,〉=60°.
答案:60° 1
7.解析:=++,
∴·=·(++)=||2=1,
∴cos〈,〉==,
∴异面直线a,b所成角是60°.
答案:60°
8. 解:(1)证明:∵=+,
∴·=(+)·=·+·
=||||·cos 60°+||||cos 120°=a2-a2=0.
∴BD⊥PC.
(2)∵+=++,
∴|+|2=||2+||2+||2+2·+2·+2·
=a2+a2+a2+0+2a2cos 60°+2a2cos 60°=5a2,
∴|+|=a.
9.解析:选D 如图,连接AG并延长交BC于点M,连接DM,
∵G是△ABC的重心,∴AG=AM,
∴=,
=+=+=+(-)
=+
=(++),
而(++)2=+++2·+2·+2·
=1+1+1+2(cos 60°+cos 60°+cos 60°)=6,
∴||=.
10.解析:∵=++=-+,
∴=(-+)2
=++-2·+2·-2·
=16+36+64=116,
∴||=2.
答案:2
11.解:设=a, =b, =c,正四面体的棱长为1,
(1)证明:因为=(a+b+c),=(b+c-5a), =(a+c-5b), =(a+b-5c),
所以·=(b+c-5a)·(a+c-5b)
=(18a·b-9|a|2)
==0,
所以⊥,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
(2) 因为=+=-(a+b+c)+c=(-2a-2b+c),
所以||= =.
又||= =,
·=(-2a-2b+c)·(b+c-5a)=,
所以cos〈,〉==.
又〈,〉∈[0,π],所以〈,〉=.
