人教A版(2019)高中数学选择性必修第二册 4.4* 《数学归纳法》名师课件(共33张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 4.4* 《数学归纳法》名师课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
法国数学家费马观察到:
于是他用归纳推理提出猜想:
任何形如的数都是质数(费马猜想)
半个世纪之后,善于计算的欧拉发现,第个费马数不是质数,从而推翻了费马的猜想
复习引入
都是质数,
有时候,方向比方法重要!
(1) 求出数列前项,你能得到什么猜想?
(2)你认为你的结论一定正确吗?如何证明猜想是正确的?
对于数列
(2)从开始逐个往下验证的想法价值不大,
我们需要寻求一种方法:通过有限个步骤的推理,证明取所有正整数都成立.
复习引入
(1)由
人教A版同步教材名师课件
数学归纳法
学习目标
学 习 目 标 核心素养
理解数学归纳法的相关概念和解题的基本思想 数学抽象
掌握数学归纳法的证明步骤 逻辑推理
学会数学归纳法在证明中的应用 数学运算
学习目标
学习目标:
1.了解数学归纳法的原理.
2.能用数学归纳法证明一些简单的数学命题.
学科核心素养:
1.通过数学归纳法定义的学习,体现了数学抽象的核心素养.
2.通过数学归纳法的应用,培养学生逻辑推理的核心素养.
我们先从多米诺骨牌游戏说起.骨牌全倒下,需要哪些条件呢?
探究新知
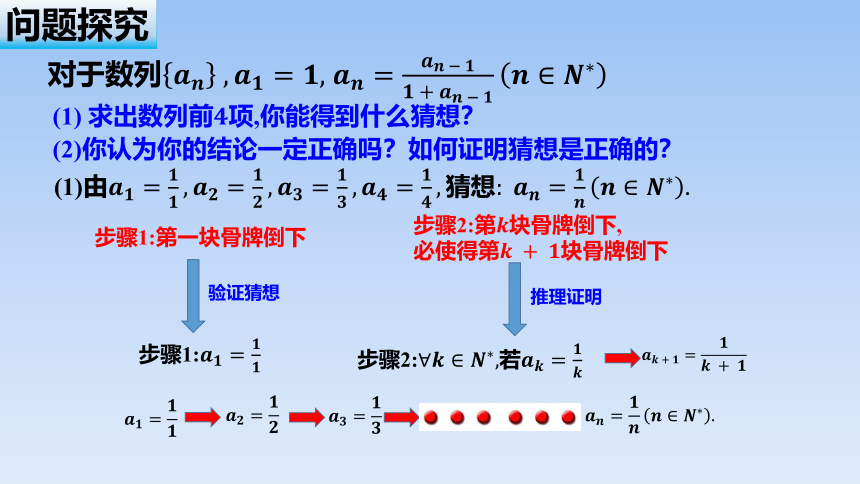
步骤1:
步骤2:若
步骤1:第一块骨牌倒下
验证猜想
步骤2:第块骨牌倒下,
必使得第块骨牌倒下
推理证明
问题探究
(1) 求出数列前项,你能得到什么猜想?
(2)你认为你的结论一定正确吗?如何证明猜想是正确的?
对于数列
(1)由
探究新知
对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:
(1)证明当取第一个值(例如)时命题成立,
(2)假设当时命题成立,证明当时命题也成立这种证明方法叫做数学归纳法.
数学归纳法
例1、用数学归纳法证明:,
其中.
典例讲解
(1)当时,左边,右边,
,所以等式成立.
(2)假设当时等式成立,
即成立.
证明
那么当时
这就是说,当时,等式也成立
由(1)和(2),可知的等式对任何都成立
用上假设
递推才真
写完结论才算完整
怎样用假设
典例讲解
左边
用数学归纳法证明与正整数有关的命题时,关键在于先“看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与的取值是否有关,由到时,等式两边会增加多少项;再“两凑”,将时的式子转化成与归纳假设的结构相同的形式——凑假设,然后利用归纳假设,经过恒等变形,得到结论所需的形式——凑结论.
方法归纳
用数学归纳法证明等式的方法
1.用数学归纳法证明: + + … + = + + … + .
(1)当时,左边==,右边=,等式成立.
(2)假设当时,等式成立,
即 + + … + = + + … + .
则当时,
+ … + +
= …
变式训练
证明
= + + … +
= + + … +
= + + …
即当时,等式成立.
故左边=右边,等式成立.
由(1)和(2)知,等式对任何正整数都成立.
变式训练
1、用数学归纳法证明: + + … + = + + … + .
证明
例2、用数学归纳法证明: + + + … + <1(.
(1)当时,左式==,右式=1 =.
因为<,所以不等式成立.
(2)假设时,不等式成立,
即 … <1
则当时, … <1
=1 =1 <1 =1
所以当时,不等式也成立.
综上所述,对任意的正整数,不等式都成立.
典例讲解
证明
典例讲解
综合法证明如下:
+ + + … + < + + + … +
= + + + … + =1 .
所以 + + + … + <1 .
例2、用数学归纳法证明: + + + … + <1(.
证明
方法归纳
利用数学归纳法证明与有关的不等式是数学归纳法的主要应用之一,应用过程中注意:
(1)证明不等式时,从到的推导过程中要应用归纳假设,有时需要对目标式进行适当的放缩来实现.
(2)与有关的不等式的证明有时并不一定非用数学归纳法不可,还经常用到不等式证明中的比较法、分析法、配方法、放缩法等,本例利用了放缩法.
变式训练
①当时,左边;
右边,因为左边>右边,所以不等式成立.
②假设当时不等式成立,
即
则当时,
2、用数学归纳法证明:对一切大于的自然数,不等式
()()·…·()>成立.
证明
变式训练
2、用数学归纳法证明:对一切大于的自然数,不等式
()()·…·()>成立.
证明
所以当时,不等式也成立.
由①②知,对于一切大于的正整数,不等式都成立.
例3、求证:当时,能被整除.
(1)当时,,命题显然成立.
(2)假设当时,能被整除,
则当时,
.
典例讲解
证明
由归纳假设,上式中的两项均能被整除,
故当时命题成立.
由(1)(2)知,对任意,命题成立.
典例讲解
例3、求证:当时,能被整除.
证明
(1)用数学归纳法证明整除问题时,首先从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除,这是用数学归纳法证明整除问题的一大技巧.
(2)在推证时,为了凑出归纳假设,采用了“增减项”技巧,所以证明整除性问题的关键是“凑项”,采用增项、减项、拆项和因式分解等手段,凑出时的情形,从而利用归纳假设使问题得证.
方法归纳
3、用数学归纳法证明能被整除.
(1)当时,,
所以能被整除.
则当时,
(2)假设当时,命题成立,
即能被整除,
由假设知,能被整除,且显然可被整除,
故能被整除.
由(1)(2)可知,对任意正整数,能被整除.
变式训练
证明
例4、数列满足,前项和.
(1)写出;
(2)猜出的表达式,并用数学归纳法证明.
(1)令,因为,所以,即.所以.
令,得,即,所以.
令,得,即,所以.
(2)猜想,下面用数学归纳法给出证明.
①当时,,结论成立.
②假设当时,结论成立,
即·=,
典例讲解
证明
则当时,
,即.
所以.
所以
由①②可知,对一切都有.
当时结论也成立.
典例讲解
例4、数列满足,前项和.
(1)写出;
(2)猜出的表达式,并用数学归纳法证明.
证明
方法归纳
“归纳—猜想—证明”的一般环节
4、将正整数作如下分组:
分别计算各组包含的正整数的和如下,
…
试猜想的结果,并用数学归纳法证明.
变式训练
变式训练
由题意知,当时,;
当时,;
当时,;
当时,.
猜想:.
下面用数学归纳法证明:
(1)当时,,等式成立.
证明
变式训练
(2)假设当时等式成立,
即,
那么,当时,
,
这就是说,当时,等式也成立.
根据(1)和(2),可知对于任意的
都成立.
(1)验证是基础
数学归纳法的原理表明,第一个步骤是要找一个数,因此“找准起点,奠基要稳”是我们正确运用数学归纳法第一个要注意的问题.
(2)递推是关键
①在证明第二步“当时命题也成立”时,一定要用上归纳假设“当时命题成立”.
②在证明第二步时,首先要明确目标式,即确定证明方向,并且要搞清从到时项的变化.
素养提炼
应用数学归纳法证明的三个注意点
素养提炼
(3)正确寻求递推关系
①在第一步验证时,不妨多计算几项,并争取正确写出来,这样对发现递推关系是有帮助的.
②探索数列通项公式要善于观察式子或命题的变化规律,观察处在哪个位置.
③在书写时,一定要把包含的式子写出来,尤其是中的最后一项.除此之外,多了哪些项,少了哪些项都要分析清楚.
归纳小结
(1)证明当取第一个值时结论正确;(归纳奠基)
(2)假设当时结论正确,证明当时结论也正确.(归纳递推)
完成这两个步骤后,就可以断定命题对从开始的所有正整数都正确.
(3)在证明递推步骤时,必须使用归纳假设,进行恒等变换.
(4)完成第(1)、(2)步骤的证明后,要对命题成立进行总结.
用数学归纳法来证明问题需要几个步骤?书写上要注意什么?
1.与正整数有关的数学命题可以考虑用数学归纳法证明,要掌握数学归纳法的书写格式,即两个步骤,一个结论.
2.数学归纳法是一种方法,更是一种思想,是一种用“有限”的手段解决“无限”的问题.
3.不完全归纳法与数学归纳法是两个貌合神离的概念:不完全归纳法是根据事物的部分特征得出整体特征的推理方法,结论未必正确;而数学归纳法的结论是绝对正确的.
归纳小结
作 业
课本P51 习题4.4:1、2
法国数学家费马观察到:
于是他用归纳推理提出猜想:
任何形如的数都是质数(费马猜想)
半个世纪之后,善于计算的欧拉发现,第个费马数不是质数,从而推翻了费马的猜想
复习引入
都是质数,
有时候,方向比方法重要!
(1) 求出数列前项,你能得到什么猜想?
(2)你认为你的结论一定正确吗?如何证明猜想是正确的?
对于数列
(2)从开始逐个往下验证的想法价值不大,
我们需要寻求一种方法:通过有限个步骤的推理,证明取所有正整数都成立.
复习引入
(1)由
人教A版同步教材名师课件
数学归纳法
学习目标
学 习 目 标 核心素养
理解数学归纳法的相关概念和解题的基本思想 数学抽象
掌握数学归纳法的证明步骤 逻辑推理
学会数学归纳法在证明中的应用 数学运算
学习目标
学习目标:
1.了解数学归纳法的原理.
2.能用数学归纳法证明一些简单的数学命题.
学科核心素养:
1.通过数学归纳法定义的学习,体现了数学抽象的核心素养.
2.通过数学归纳法的应用,培养学生逻辑推理的核心素养.
我们先从多米诺骨牌游戏说起.骨牌全倒下,需要哪些条件呢?
探究新知
步骤1:
步骤2:若
步骤1:第一块骨牌倒下
验证猜想
步骤2:第块骨牌倒下,
必使得第块骨牌倒下
推理证明
问题探究
(1) 求出数列前项,你能得到什么猜想?
(2)你认为你的结论一定正确吗?如何证明猜想是正确的?
对于数列
(1)由
探究新知
对于由不完全归纳法得到的某些与自然数有关自然数的数学命题我们常采用下面的方法来证明它们的正确性:
(1)证明当取第一个值(例如)时命题成立,
(2)假设当时命题成立,证明当时命题也成立这种证明方法叫做数学归纳法.
数学归纳法
例1、用数学归纳法证明:,
其中.
典例讲解
(1)当时,左边,右边,
,所以等式成立.
(2)假设当时等式成立,
即成立.
证明
那么当时
这就是说,当时,等式也成立
由(1)和(2),可知的等式对任何都成立
用上假设
递推才真
写完结论才算完整
怎样用假设
典例讲解
左边
用数学归纳法证明与正整数有关的命题时,关键在于先“看项”,弄清等式两边的构成规律,等式的两边各有多少项,项的多少与的取值是否有关,由到时,等式两边会增加多少项;再“两凑”,将时的式子转化成与归纳假设的结构相同的形式——凑假设,然后利用归纳假设,经过恒等变形,得到结论所需的形式——凑结论.
方法归纳
用数学归纳法证明等式的方法
1.用数学归纳法证明: + + … + = + + … + .
(1)当时,左边==,右边=,等式成立.
(2)假设当时,等式成立,
即 + + … + = + + … + .
则当时,
+ … + +
= …
变式训练
证明
= + + … +
= + + … +
= + + …
即当时,等式成立.
故左边=右边,等式成立.
由(1)和(2)知,等式对任何正整数都成立.
变式训练
1、用数学归纳法证明: + + … + = + + … + .
证明
例2、用数学归纳法证明: + + + … + <1(.
(1)当时,左式==,右式=1 =.
因为<,所以不等式成立.
(2)假设时,不等式成立,
即 … <1
则当时, … <1
=1 =1 <1 =1
所以当时,不等式也成立.
综上所述,对任意的正整数,不等式都成立.
典例讲解
证明
典例讲解
综合法证明如下:
+ + + … + < + + + … +
= + + + … + =1 .
所以 + + + … + <1 .
例2、用数学归纳法证明: + + + … + <1(.
证明
方法归纳
利用数学归纳法证明与有关的不等式是数学归纳法的主要应用之一,应用过程中注意:
(1)证明不等式时,从到的推导过程中要应用归纳假设,有时需要对目标式进行适当的放缩来实现.
(2)与有关的不等式的证明有时并不一定非用数学归纳法不可,还经常用到不等式证明中的比较法、分析法、配方法、放缩法等,本例利用了放缩法.
变式训练
①当时,左边;
右边,因为左边>右边,所以不等式成立.
②假设当时不等式成立,
即
则当时,
2、用数学归纳法证明:对一切大于的自然数,不等式
()()·…·()>成立.
证明
变式训练
2、用数学归纳法证明:对一切大于的自然数,不等式
()()·…·()>成立.
证明
所以当时,不等式也成立.
由①②知,对于一切大于的正整数,不等式都成立.
例3、求证:当时,能被整除.
(1)当时,,命题显然成立.
(2)假设当时,能被整除,
则当时,
.
典例讲解
证明
由归纳假设,上式中的两项均能被整除,
故当时命题成立.
由(1)(2)知,对任意,命题成立.
典例讲解
例3、求证:当时,能被整除.
证明
(1)用数学归纳法证明整除问题时,首先从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除,这是用数学归纳法证明整除问题的一大技巧.
(2)在推证时,为了凑出归纳假设,采用了“增减项”技巧,所以证明整除性问题的关键是“凑项”,采用增项、减项、拆项和因式分解等手段,凑出时的情形,从而利用归纳假设使问题得证.
方法归纳
3、用数学归纳法证明能被整除.
(1)当时,,
所以能被整除.
则当时,
(2)假设当时,命题成立,
即能被整除,
由假设知,能被整除,且显然可被整除,
故能被整除.
由(1)(2)可知,对任意正整数,能被整除.
变式训练
证明
例4、数列满足,前项和.
(1)写出;
(2)猜出的表达式,并用数学归纳法证明.
(1)令,因为,所以,即.所以.
令,得,即,所以.
令,得,即,所以.
(2)猜想,下面用数学归纳法给出证明.
①当时,,结论成立.
②假设当时,结论成立,
即·=,
典例讲解
证明
则当时,
,即.
所以.
所以
由①②可知,对一切都有.
当时结论也成立.
典例讲解
例4、数列满足,前项和.
(1)写出;
(2)猜出的表达式,并用数学归纳法证明.
证明
方法归纳
“归纳—猜想—证明”的一般环节
4、将正整数作如下分组:
分别计算各组包含的正整数的和如下,
…
试猜想的结果,并用数学归纳法证明.
变式训练
变式训练
由题意知,当时,;
当时,;
当时,;
当时,.
猜想:.
下面用数学归纳法证明:
(1)当时,,等式成立.
证明
变式训练
(2)假设当时等式成立,
即,
那么,当时,
,
这就是说,当时,等式也成立.
根据(1)和(2),可知对于任意的
都成立.
(1)验证是基础
数学归纳法的原理表明,第一个步骤是要找一个数,因此“找准起点,奠基要稳”是我们正确运用数学归纳法第一个要注意的问题.
(2)递推是关键
①在证明第二步“当时命题也成立”时,一定要用上归纳假设“当时命题成立”.
②在证明第二步时,首先要明确目标式,即确定证明方向,并且要搞清从到时项的变化.
素养提炼
应用数学归纳法证明的三个注意点
素养提炼
(3)正确寻求递推关系
①在第一步验证时,不妨多计算几项,并争取正确写出来,这样对发现递推关系是有帮助的.
②探索数列通项公式要善于观察式子或命题的变化规律,观察处在哪个位置.
③在书写时,一定要把包含的式子写出来,尤其是中的最后一项.除此之外,多了哪些项,少了哪些项都要分析清楚.
归纳小结
(1)证明当取第一个值时结论正确;(归纳奠基)
(2)假设当时结论正确,证明当时结论也正确.(归纳递推)
完成这两个步骤后,就可以断定命题对从开始的所有正整数都正确.
(3)在证明递推步骤时,必须使用归纳假设,进行恒等变换.
(4)完成第(1)、(2)步骤的证明后,要对命题成立进行总结.
用数学归纳法来证明问题需要几个步骤?书写上要注意什么?
1.与正整数有关的数学命题可以考虑用数学归纳法证明,要掌握数学归纳法的书写格式,即两个步骤,一个结论.
2.数学归纳法是一种方法,更是一种思想,是一种用“有限”的手段解决“无限”的问题.
3.不完全归纳法与数学归纳法是两个貌合神离的概念:不完全归纳法是根据事物的部分特征得出整体特征的推理方法,结论未必正确;而数学归纳法的结论是绝对正确的.
归纳小结
作 业
课本P51 习题4.4:1、2
