11.2.1三角形的内角(2) 课件(20张PPT)
文档属性
| 名称 | 11.2.1三角形的内角(2) 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-02 22:41:36 | ||
图片预览






文档简介
(共20张PPT)
11.2.1三角形的内角(2)
人教版八年级上册
教学目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
新知导入
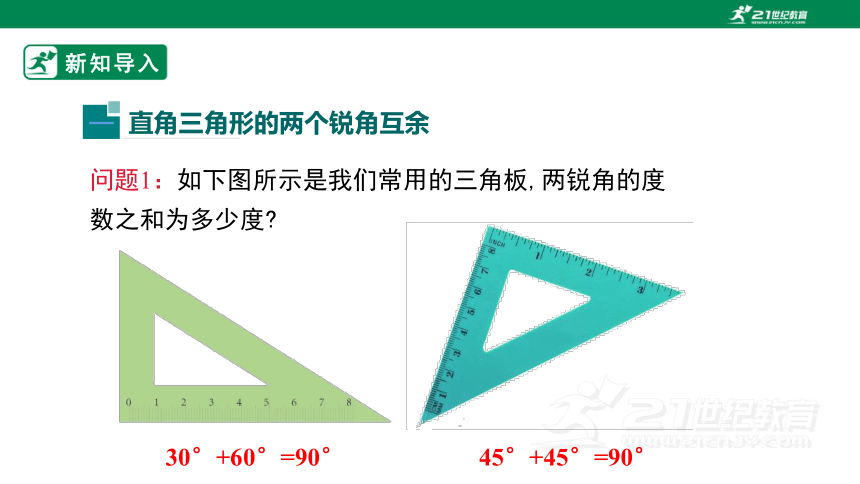
问题1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
直角三角形的两个锐角互余
一
新知导入
问题2:如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
新知讲解
A
B
C
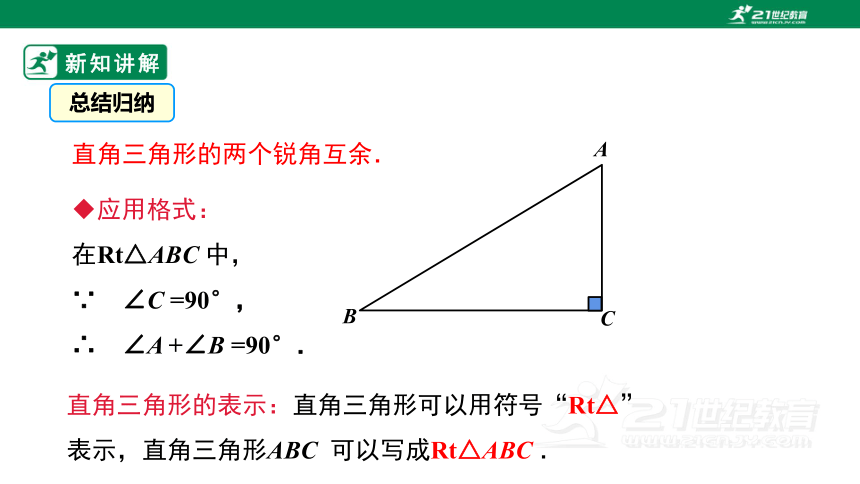
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
总结归纳
典例讲解
例1(1)如图 ,∠B=∠C=90°,AD交BC于点O,∠A
与∠D有什么关系?
图
典例讲解
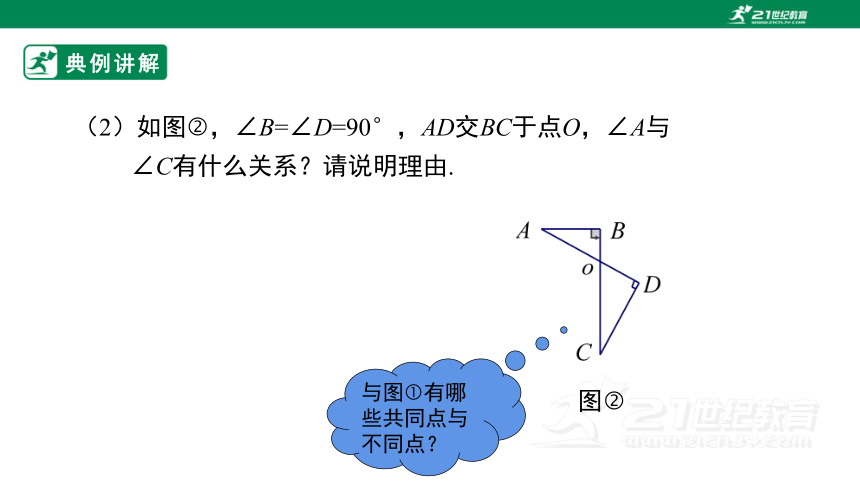
(2)如图 ,∠B=∠D=90°,AD交BC于点O,∠A与
∠C有什么关系?请说明理由.
图
与图 有哪些共同点与不同点?
典例讲解
例2 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°,
解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等).
典例讲解
【变式题】如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
新知讲解
思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
∠A=∠D
总结归纳
新知讲解
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
二
新知讲解
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
典例讲解
例3 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?
A
C
B
D
E
(
(
1
2
解: △ADE是直角三角形. 理由如下:
∵∠C=90°,∴∠A+∠2=90°.
又∠1=∠2,∴∠A+∠1=90°.
∴∠ADE=90°,即△ADE是直角三角形.
典例讲解
例4 如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?
解答:证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴∠ABD=90°,
∴AB⊥CD.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
随堂练习
1.△ABC中,∠A : ∠B : ∠C = 1 : 2 : 3,则∠A=______,∠B = ______,∠C = ______.
90°
30°
60°
2.如图,∠ACB=90°,CD⊥AB于D,则图中除直角外相等的角有__________________
______________,互余的角有:____________
________________________________________.
∠A =∠BCD,
∠A与∠B,∠A与∠ACD,∠B与∠BCD,∠ACD与∠BCD
∠B =∠ACD
随堂练习
3.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°. 求∠C的度数.
2
3
1
4
解:∵∠1+∠2+∠B= 180°,∠3+∠4+∠D=180°,
∴∠l+∠2+∠B+∠3+∠4+∠D=180°+180°.
∴(∠1+∠4)+(∠2+∠3)+∠B+∠D= 360°.
即∠BCD+∠BAD+40°+40°= 360°.
则∠BCD= 360°- 150°-80°= 130°.
【课本P13 练习 第2题】
随堂练习
4.如图,在△ABC 中,∠ABC= 70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数.
解:∵∠ABC = 70°,∠C = 65°,
∴∠A = 180°–∠ABC –∠C = 45°.
∵BD⊥AC,
∴∠ADB =∠CDB = 90°,
∴∠ABD = 90°–∠A = ∠45°,
∠CBD = 90° – ∠C = 25°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.1三角形的内角(2)
人教版八年级上册
教学目标
1.了解直角三角形两个锐角的关系.(重点)
2.掌握直角三角形的判定.(难点)
3.会运用直角三角形的性质和判定进行相关计算.(难点)
新知导入
问题1:如下图所示是我们常用的三角板,两锐角的度数之和为多少度
30°+60°=90°
45°+45°=90°
直角三角形的两个锐角互余
一
新知导入
问题2:如图,在Rt△ABC中, ∠C=90°,两锐角的和等于多少呢?
在Rt△ABC中,因为 ∠C=90°,由三角形内角和定理,得∠A +∠B+∠C=90°,即
∠A +∠B=90°.
思考:由此,你可以得到直角三角形有什么性质呢?
新知讲解
A
B
C
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
总结归纳
典例讲解
例1(1)如图 ,∠B=∠C=90°,AD交BC于点O,∠A
与∠D有什么关系?
图
典例讲解
(2)如图 ,∠B=∠D=90°,AD交BC于点O,∠A与
∠C有什么关系?请说明理由.
图
与图 有哪些共同点与不同点?
典例讲解
例2 如图, ∠C=∠D=90 °,AD,BC相交于点E. ∠CAE与∠DBE有什么关系?为什么?
A
B
C
D
E
解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°,
解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等).
典例讲解
【变式题】如图,△ABC中,CD⊥AB于D,BE⊥AC于E,CD,BE相交于点F,∠A与∠BFC又有什么关系?为什么?
新知讲解
思考:通过前面的例题,你能画出这些题型的基本
图形吗?
基本图形
∠A=∠C
∠A=∠D
总结归纳
新知讲解
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC
是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形
二
新知讲解
A
B
C
应用格式:
在△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
总结归纳
典例讲解
例3 如图,∠C=90 °, ∠1= ∠2,△ADE是直角三
角形吗?为什么?
A
C
B
D
E
(
(
1
2
解: △ADE是直角三角形. 理由如下:
∵∠C=90°,∴∠A+∠2=90°.
又∠1=∠2,∴∠A+∠1=90°.
∴∠ADE=90°,即△ADE是直角三角形.
典例讲解
例4 如图,CE⊥AD,垂足为E,∠A=∠C,△ABD是
直角三角形吗?为什么?
解答:证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°,
∵∠A=∠C,
∴∠A+∠D=90°,
∴∠ABD=90°,
∴AB⊥CD.
课堂小结
直角三角形的性质与判定
性质
直角三角形的两个锐角互余
判定
有两个角互余的三角形是直角三角形
随堂练习
1.△ABC中,∠A : ∠B : ∠C = 1 : 2 : 3,则∠A=______,∠B = ______,∠C = ______.
90°
30°
60°
2.如图,∠ACB=90°,CD⊥AB于D,则图中除直角外相等的角有__________________
______________,互余的角有:____________
________________________________________.
∠A =∠BCD,
∠A与∠B,∠A与∠ACD,∠B与∠BCD,∠ACD与∠BCD
∠B =∠ACD
随堂练习
3.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°. 求∠C的度数.
2
3
1
4
解:∵∠1+∠2+∠B= 180°,∠3+∠4+∠D=180°,
∴∠l+∠2+∠B+∠3+∠4+∠D=180°+180°.
∴(∠1+∠4)+(∠2+∠3)+∠B+∠D= 360°.
即∠BCD+∠BAD+40°+40°= 360°.
则∠BCD= 360°- 150°-80°= 130°.
【课本P13 练习 第2题】
随堂练习
4.如图,在△ABC 中,∠ABC= 70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数.
解:∵∠ABC = 70°,∠C = 65°,
∴∠A = 180°–∠ABC –∠C = 45°.
∵BD⊥AC,
∴∠ADB =∠CDB = 90°,
∴∠ABD = 90°–∠A = ∠45°,
∠CBD = 90° – ∠C = 25°.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
