人教A版(2019)高中数学选择性必修第二册 【整合课件】5.1.1-5.1.2_变化率问题-导数的概念 课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.1.1-5.1.2_变化率问题-导数的概念 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 09:26:41 | ||
图片预览











文档简介
(共37张PPT)
第五章 §5.1 变化率与导数
5.1.1 变化率问题 5.1.2 导数的概念
学习目标
1.了解导数概念的实际背景.
2.会求函数在某一点附近的平均变化率.
3.会利用导数的定义求函数在某点处的导数.
问题导学
知识点一 函数的平均变化率
假设如图是一座山的剖面示意图,并建立如图
所示平面直角坐标系.A是出发点,H是山顶.爬山
路线用函数y=f(x)表示.
自变量x表示某旅游者的水平位置,函数值y=
f(x)表示此时旅游者所在的高度.设点A的坐标为(x1,y1),点B的坐标为(x2,y2).
思考1 若旅游者从点A爬到点B,自变量x和函数值y的改变量分别是多少?
答案 自变量x的改变量为x2-x1,记作Δx,函数值的改变量为y2-y1,记作Δy.
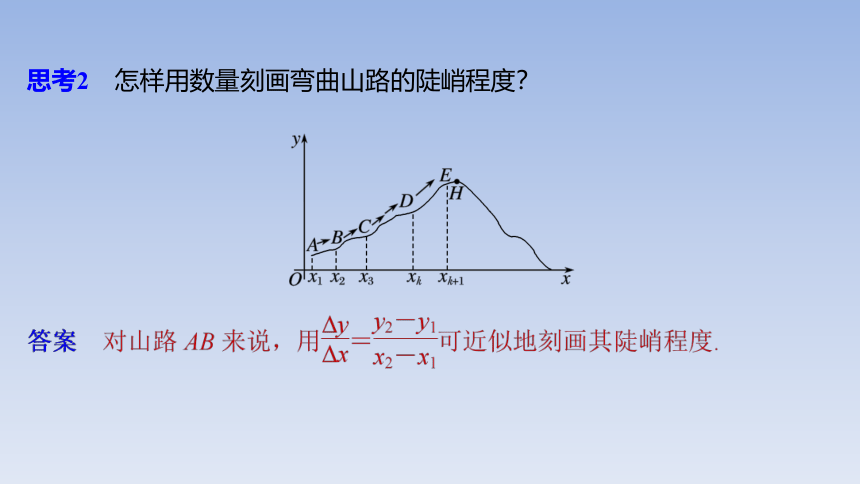
思考2 怎样用数量刻画弯曲山路的陡峭程度?
梳理 函数y=f(x)从x1到x2的平均变化率
(2)实质: 的增量与 的增量之比.
(3)作用:刻画函数值在区间[x1,x2]上变化的快慢.
(4)几何意义:已知P1(x1,f(x1)),P2(x2,f(x2))是函数y=f(x)的图象上两
点,则平均变化率 表示割线P1P2的 .
函数值
自变量
斜率
思考2 当Δt趋近于0时,思考1中的平均速度趋近于多少?怎样理解这一速度?
知识点二 瞬时速度
思考1 物体的路程s与时间t的关系是s(t)=5t2.试求物体在[1,1+Δt]这段时间内的平均速度.
梳理 瞬时速度
(1)物体在 的速度称为瞬时速度.
(2)一般地,设物体的运动规律是s=s(t),则物体在t0到t0+Δt这段时间内
某一时刻
极限
知识点三 函数在某点处的导数
f′(x0)或
1.在平均变化率中,函数值的增量为正值.( )
2.瞬时变化率是刻画某函数值在区间[x1,x2]上变化快慢的物理量.( )
3.函数y=f(x)在x=x0处的导数值与Δx的正、负无关.( )
[思考辨析 判断正误]
×
√
×
题型探究
类型一 函数的平均变化率
解 在x=1附近的平均变化率为
在x=2附近的平均变化率为
在x=3附近的平均变化率为
由于k1反思与感悟 求平均变化率的主要步骤
(1)先计算函数值的改变量Δy=f(x2)-f(x1).
(2)再计算自变量的改变量Δx=x2-x1.
跟踪训练1 (1)已知函数y=f(x)=x2+2x-5的图象上的一点A(-1,-6)及邻近一点B(-1+Δx,-6+Δy),则 =____.
Δx
(2)如图所示是函数y=f(x)的图象,则函数f(x)在区间[-1,1]上的平均变化率为___;函数f(x)在区间[0,2]上的平均变化率为___.
∵Δy=f(1+Δx)-f(1)
=(1+Δx)2-(1+Δx)-(12-1)=Δx+(Δx)2,
命题角度2 平均变化率的几何意义
例2 过曲线y=f(x)=x2-x上的两点P(1,0)和Q(1+Δx,Δy)作曲线的割线,已知割线PQ的斜率为2,求Δx的值.
又∵割线PQ的斜率为2,∴1+Δx=2,∴Δx=1.
跟踪训练2 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图所示,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲,v乙的关系是
A.v甲>v乙 B.v甲C.v甲=v乙 D.大小关系不确定
解析 设直线AC,BC的斜率分别为kAC,kBC,由平均变化率的几何意义知,s1(t)在[0,t0]上的平均变化率v甲=kAC,s2(t)在[0,t0]上的平均变化率v乙=kBC.因为kAC√
类型二 求瞬时速度
∴物体在t=1处的瞬时变化率为3.
即物体在t=1 s时的瞬时速度为3 m/s.
例3 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
引申探究
1.若例3中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度.
∴物体在t=0时的瞬时变化率为1,
即物体的初速度为1 m/s.
2.若例3中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
反思与感悟 (1)不能将物体的瞬时速度转化为函数的瞬时变化率是导致无从下手解答本类题的常见错误.
(2)求运动物体瞬时速度的三个步骤
①求时间改变量Δt和位移改变量Δs=s(t0+Δt)-s(t0);
跟踪训练3 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2时的瞬时速度即为函数在t=2处的瞬时变化率.
∵质点M在t=2附近的平均变化率为
类型三 导数定义的应用
√
反思与感悟 (1)用导数定义求函数在某一点处的导数的步骤
①求函数的增量Δy=f(x0+Δx)-f(x0);
(2)瞬时变化率的变形形式
跟踪训练4 已知f(x)=3x2,f′(x0)=6,求x0.
又f′(x0)=6,∴6x0=6,即x0=1.
1.设函数y=f(x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为
A.2.1 B.1.1
C.2 D.0
1
2
3
4
5
√
达标检测
A.18 m/s是物体从开始到3 s这段时间内的平均速度
B.18 m/s是物体从3 s到(3+Δt)s这段时间内的速度
C.18 m/s是物体在3 s这一时刻的瞬时速度
D.18 m/s是物体从3 s到(3+Δt)s这段时间内的平均速度
1
2
3
4
5
√
达标检测
3.设函数f(x)=ax+3,若f′(1)=3,则a等于
A.2 B.-2
C.-3 D.3
1
2
3
4
5
√
因为f′(1)=3,所以a=3.
达标检测
4.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间上,平均变化率最大的一个区间是________.
解析 由平均变化率的定义可知,函数y=f(x)在区间[x1,x2],[x2,x3],[x3,x4]上平均变化率分别为 结合图
象可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].
1
2
3
4
5
[x3,x4]
1
2
3
4
5
5.一物体的运动方程为s(t)=7t2-13t+8,则t0=__时该物体的瞬时速度为1.
1
=14t0-13=1,得t0=1.
理解平均变化率要注意以下几点:
规律与方法
(3)函数的平均变化率可以表现出函数的变化趋势.自变量的改变量Δx取值越小,越能准确体现函数的变化情况.
利用导数定义求导数:
(2)函数在x0处的导数f′(x0)只与x0有关,与Δx无关.
(3)导数可以描述事物的瞬时变化率,应用非常广泛.
第五章 §5.1 变化率与导数
5.1.1 变化率问题 5.1.2 导数的概念
学习目标
1.了解导数概念的实际背景.
2.会求函数在某一点附近的平均变化率.
3.会利用导数的定义求函数在某点处的导数.
问题导学
知识点一 函数的平均变化率
假设如图是一座山的剖面示意图,并建立如图
所示平面直角坐标系.A是出发点,H是山顶.爬山
路线用函数y=f(x)表示.
自变量x表示某旅游者的水平位置,函数值y=
f(x)表示此时旅游者所在的高度.设点A的坐标为(x1,y1),点B的坐标为(x2,y2).
思考1 若旅游者从点A爬到点B,自变量x和函数值y的改变量分别是多少?
答案 自变量x的改变量为x2-x1,记作Δx,函数值的改变量为y2-y1,记作Δy.
思考2 怎样用数量刻画弯曲山路的陡峭程度?
梳理 函数y=f(x)从x1到x2的平均变化率
(2)实质: 的增量与 的增量之比.
(3)作用:刻画函数值在区间[x1,x2]上变化的快慢.
(4)几何意义:已知P1(x1,f(x1)),P2(x2,f(x2))是函数y=f(x)的图象上两
点,则平均变化率 表示割线P1P2的 .
函数值
自变量
斜率
思考2 当Δt趋近于0时,思考1中的平均速度趋近于多少?怎样理解这一速度?
知识点二 瞬时速度
思考1 物体的路程s与时间t的关系是s(t)=5t2.试求物体在[1,1+Δt]这段时间内的平均速度.
梳理 瞬时速度
(1)物体在 的速度称为瞬时速度.
(2)一般地,设物体的运动规律是s=s(t),则物体在t0到t0+Δt这段时间内
某一时刻
极限
知识点三 函数在某点处的导数
f′(x0)或
1.在平均变化率中,函数值的增量为正值.( )
2.瞬时变化率是刻画某函数值在区间[x1,x2]上变化快慢的物理量.( )
3.函数y=f(x)在x=x0处的导数值与Δx的正、负无关.( )
[思考辨析 判断正误]
×
√
×
题型探究
类型一 函数的平均变化率
解 在x=1附近的平均变化率为
在x=2附近的平均变化率为
在x=3附近的平均变化率为
由于k1
(1)先计算函数值的改变量Δy=f(x2)-f(x1).
(2)再计算自变量的改变量Δx=x2-x1.
跟踪训练1 (1)已知函数y=f(x)=x2+2x-5的图象上的一点A(-1,-6)及邻近一点B(-1+Δx,-6+Δy),则 =____.
Δx
(2)如图所示是函数y=f(x)的图象,则函数f(x)在区间[-1,1]上的平均变化率为___;函数f(x)在区间[0,2]上的平均变化率为___.
∵Δy=f(1+Δx)-f(1)
=(1+Δx)2-(1+Δx)-(12-1)=Δx+(Δx)2,
命题角度2 平均变化率的几何意义
例2 过曲线y=f(x)=x2-x上的两点P(1,0)和Q(1+Δx,Δy)作曲线的割线,已知割线PQ的斜率为2,求Δx的值.
又∵割线PQ的斜率为2,∴1+Δx=2,∴Δx=1.
跟踪训练2 甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图所示,则在[0,t0]这个时间段内,甲、乙两人的平均速度v甲,v乙的关系是
A.v甲>v乙 B.v甲
解析 设直线AC,BC的斜率分别为kAC,kBC,由平均变化率的几何意义知,s1(t)在[0,t0]上的平均变化率v甲=kAC,s2(t)在[0,t0]上的平均变化率v乙=kBC.因为kAC
类型二 求瞬时速度
∴物体在t=1处的瞬时变化率为3.
即物体在t=1 s时的瞬时速度为3 m/s.
例3 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,求物体在t=1 s时的瞬时速度.
引申探究
1.若例3中的条件不变,试求物体的初速度.
解 求物体的初速度,即求物体在t=0时的瞬时速度.
∴物体在t=0时的瞬时变化率为1,
即物体的初速度为1 m/s.
2.若例3中的条件不变,试问物体在哪一时刻的瞬时速度为9 m/s.
解 设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
反思与感悟 (1)不能将物体的瞬时速度转化为函数的瞬时变化率是导致无从下手解答本类题的常见错误.
(2)求运动物体瞬时速度的三个步骤
①求时间改变量Δt和位移改变量Δs=s(t0+Δt)-s(t0);
跟踪训练3 一质点M按运动方程s(t)=at2+1做直线运动(位移单位:m,时间单位:s),若质点M在t=2 s时的瞬时速度为8 m/s,求常数a的值.
解 质点M在t=2时的瞬时速度即为函数在t=2处的瞬时变化率.
∵质点M在t=2附近的平均变化率为
类型三 导数定义的应用
√
反思与感悟 (1)用导数定义求函数在某一点处的导数的步骤
①求函数的增量Δy=f(x0+Δx)-f(x0);
(2)瞬时变化率的变形形式
跟踪训练4 已知f(x)=3x2,f′(x0)=6,求x0.
又f′(x0)=6,∴6x0=6,即x0=1.
1.设函数y=f(x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为
A.2.1 B.1.1
C.2 D.0
1
2
3
4
5
√
达标检测
A.18 m/s是物体从开始到3 s这段时间内的平均速度
B.18 m/s是物体从3 s到(3+Δt)s这段时间内的速度
C.18 m/s是物体在3 s这一时刻的瞬时速度
D.18 m/s是物体从3 s到(3+Δt)s这段时间内的平均速度
1
2
3
4
5
√
达标检测
3.设函数f(x)=ax+3,若f′(1)=3,则a等于
A.2 B.-2
C.-3 D.3
1
2
3
4
5
√
因为f′(1)=3,所以a=3.
达标检测
4.如图,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间上,平均变化率最大的一个区间是________.
解析 由平均变化率的定义可知,函数y=f(x)在区间[x1,x2],[x2,x3],[x3,x4]上平均变化率分别为 结合图
象可以发现函数y=f(x)的平均变化率最大的一个区间是[x3,x4].
1
2
3
4
5
[x3,x4]
1
2
3
4
5
5.一物体的运动方程为s(t)=7t2-13t+8,则t0=__时该物体的瞬时速度为1.
1
=14t0-13=1,得t0=1.
理解平均变化率要注意以下几点:
规律与方法
(3)函数的平均变化率可以表现出函数的变化趋势.自变量的改变量Δx取值越小,越能准确体现函数的变化情况.
利用导数定义求导数:
(2)函数在x0处的导数f′(x0)只与x0有关,与Δx无关.
(3)导数可以描述事物的瞬时变化率,应用非常广泛.
