人教A版(2019)高中数学选择性必修第二册 【整合课件】5.1.3导数的几何意义 课件(共40张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.1.3导数的几何意义 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
5.1.3 导数的几何意义
学习目标
1.了解导函数的概念,理解导数的几何意义.
2.会求简单函数的导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
问题导学
知识点一 导数的几何意义
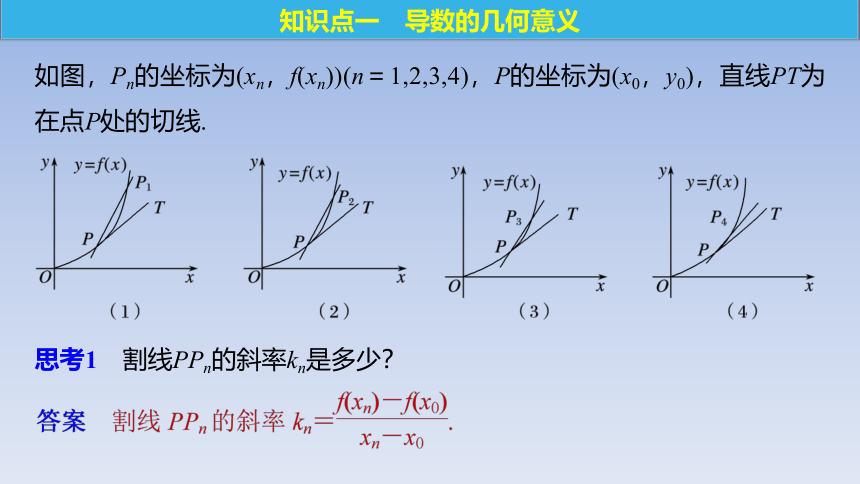
如图,Pn的坐标为(xn,f(xn))(n=1,2,3,4),P的坐标为(x0,y0),直线PT为在点P处的切线.
思考1 割线PPn的斜率kn是多少?
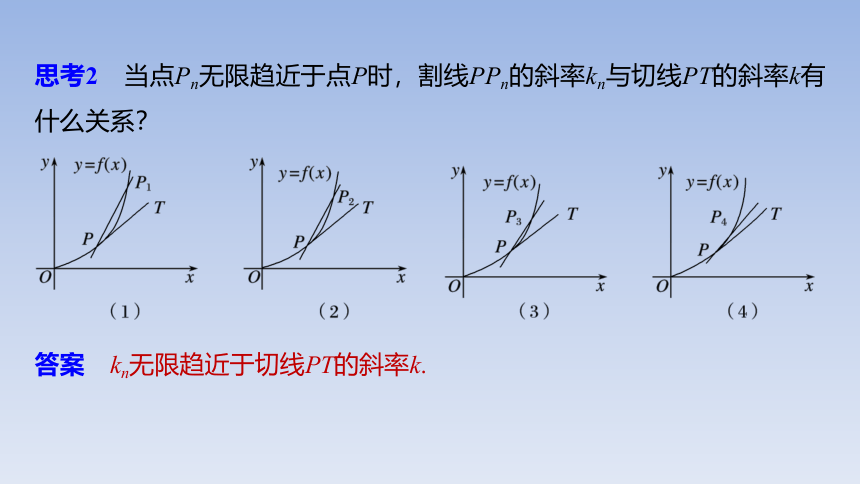
思考2 当点Pn无限趋近于点P时,割线PPn的斜率kn与切线PT的斜率k有什么关系?
答案 kn无限趋近于切线PT的斜率k.
梳理 (1)切线的定义:设PPn是曲线y=f(x)的割线,当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为曲线y=f(x) 的切线.
(2)导数f′(x0)的几何意义:导数f′(x0)表示曲线y=f(x)在点 处
的切线的斜率k,即k= = .
(3)切线方程:曲线y=f(x)在点(x0,f(x0))处的切线方程为_____________ ______________.
在点P处
(x0,f(x0))
f′(x0)
y-f(x0)=
f′(x0)(x-x0)
思考 已知函数f(x)=x2,分别计算f′(1)与f′(x),它们有什么不同.
知识点二 导函数
f′(1)是一个值,而f′(x)是一个函数.
梳理 对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,则当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称
导数), 即f′(x)=y′= .
特别提醒:
区别 联系
f′(x0) f′(x0)是具体的值,是数值 在x=x0处的导数f′(x0)是导函数f′(x)在x=x0处的函数值,因此求函数在某一点处的导数,一般先求导函数,再计算导函数在这一点的函数值
f′(x) f′(x)是函数f(x)在某区间I上每一点都存在导数而定义的一个新函数,是函数
1.函数在一点处的导数f′(x0)是一个常数.( )
2.函数y=f(x)在点x0处的导数f′(x0)就是导函数f′(x)在点x=x0处的函数值.
( )
3.直线与曲线相切,则直线与已知曲线只有一个公共点.( )
[思考辨析 判断正误]
√
√
×
题型探究
类型一 求切线方程
解 将x=2代入曲线C的方程得y=4,
∴切点P(2,4).
∴k= =4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.
反思与感悟 求曲线在某点处的切线方程的步骤
跟踪训练1 曲线y=x2+1在点P(2,5)处的切线与y轴交点的纵坐标是_____.
-3
∴k= =4.
∴曲线y=x2+1在点(2,5)处的切线方程为y-5=4(x-2),即y=4x-3.
∴切线与y轴交点的纵坐标是-3.
命题角度2 曲线过某点的切线方程
例2 求过点(-1,0)与曲线y=x2+x+1相切的直线方程.
解 设切点为(x0, +x0+1),
解得x0=0或x0=-2.
当x0=0时,切线斜率k=1,过(-1,0)的切线方程为y-0=x+1,
即x-y+1=0.
当x0=-2时,切线斜率k=-3,过(-1,0)的切线方程为y-0=-3(x+1),即3x+y+3=0.
故所求切线方程为x-y+1=0或3x+y+3=0.
反思与感悟 过点(x1,y1)的曲线y=f(x)的切线方程的求法步骤
(1)设切点(x0,f(x0)).
(3)解方程得k=f′(x0),x0,y0,从而写出切线方程.
跟踪训练2 求函数y=f(x)=x3-3x2+x的图象上过原点的切线方程.
∵Δy=f(x0+Δx)-f(x0)
故所求切线方程为x-y=0或5x+4y=0.
类型二 利用图象理解导数的几何意义
例3 已知函数f(x)的图象如图所示,则下列不等关系中正确的是
A.0B.0C.0D.0√
f′(2)为函数f(x)的图象在点B(2,f(2))处的切线的斜率,
f′(3)为函数f(x)的图象在点A(3,f(3))处的切线的斜率,
根据图象可知0反思与感悟 导数的几何意义就是切线的斜率,所以比较导数大小的问题可以用数形结合思想来解决.
跟踪训练3 若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是
√
解析 依题意,y=f′(x)在[a,b]上是增函数,则在函数f(x)的图象上,各点的切线的斜率随着x的增大而增大,观察四个选项的图象,只有A满足.
例4 已知曲线f(x)=x2-1在x=x0处的切线与曲线g(x)=1-x3在x=x0处的切线互相平行,求x0的值.
类型三 求切点坐标
解 对于曲线f(x)=x2-1,
对于曲线g(x)=1-x3,
引申探究
若将本例条件中的“平行”改为“垂直”,求x0的值.
反思与感悟 求切点坐标的一般步骤
(1)设出切点坐标.
(2)利用导数或斜率公式求出斜率.
(3)利用斜率关系列方程,求出切点的横坐标.
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
跟踪训练4 直线l:y=x+a(a≠0)和曲线C:f(x)=x3-x2+1相切,则a的
值为____,切点坐标为__________.
解析 设直线l与曲线C的切点为(x0,y0),
又点(x0,f(x0))在直线y=x+a上,将x0=1,y0=1.
代入得a=0,与已知条件矛盾,舍去.
达标检测
1.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么
A.f′(x0)>0 B.f′(x0)<0
C.f′(x0)=0 D.f′(x0)不存在
1
2
3
4
5
√
1
2
3
4
5
2.设曲线f(x)=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于
√
所以2a=2,所以a=1.
3.已知函数y=f(x)的图象如图所示,则f′(xA)与
f′(xB)的大小关系是
A.f′(xA)>f′(xB)
B.f′(xA)C.f′(xA)=f′(xB)
D.不能确定
解析 由导数的几何意义,知f′(xA),f′(xB)分别是切线在点A,B处切线的斜率,由图象可知f′(xA)1
2
3
4
5
√
4.已知曲线y=f(x)=2x2+a在点P处的切线方程为8x-y-15=0,则实数a的值为_____.
1
2
3
4
5
-7
由导数的几何意义可得,
∴x0=2,∴P(2,8+a).
将x=2,y=8+a,代入8x-y-15=0,
得a=-7.
5.已知曲线f(x)=x3在点(a,a3)(a≠0)处的切线与x轴,直线x=a围成的三角形的面积为 ,则a=_____.
±1
∴曲线f(x)=x3在点(a,a3)处的切线斜率为f′(a)=3a2,
∴切线方程为y-a3=3a2(x-a),即y=3a2x-2a3.
1
2
3
4
5
1.导数f′(x0)的几何意义是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,即k=
物理意义是运动物体在某一时刻的瞬时速度.
2.“函数f(x)在点x0处的导数”是一个数值,不是变数,“导函数”是一个函数,二者有本质的区别,但又有密切关系,f′(x0)是其导数y=f′(x)在x=x0处的一个函数值.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则设出切点坐标(x0,f(x0)),表示出切线方程,然后求出切点.
5.1.3 导数的几何意义
学习目标
1.了解导函数的概念,理解导数的几何意义.
2.会求简单函数的导函数.
3.根据导数的几何意义,会求曲线上某点处的切线方程.
问题导学
知识点一 导数的几何意义
如图,Pn的坐标为(xn,f(xn))(n=1,2,3,4),P的坐标为(x0,y0),直线PT为在点P处的切线.
思考1 割线PPn的斜率kn是多少?
思考2 当点Pn无限趋近于点P时,割线PPn的斜率kn与切线PT的斜率k有什么关系?
答案 kn无限趋近于切线PT的斜率k.
梳理 (1)切线的定义:设PPn是曲线y=f(x)的割线,当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确定位置的直线PT称为曲线y=f(x) 的切线.
(2)导数f′(x0)的几何意义:导数f′(x0)表示曲线y=f(x)在点 处
的切线的斜率k,即k= = .
(3)切线方程:曲线y=f(x)在点(x0,f(x0))处的切线方程为_____________ ______________.
在点P处
(x0,f(x0))
f′(x0)
y-f(x0)=
f′(x0)(x-x0)
思考 已知函数f(x)=x2,分别计算f′(1)与f′(x),它们有什么不同.
知识点二 导函数
f′(1)是一个值,而f′(x)是一个函数.
梳理 对于函数y=f(x),当x=x0时,f′(x0)是一个确定的数,则当x变化时,f′(x)便是一个关于x的函数,我们称它为函数y=f(x)的导函数(简称
导数), 即f′(x)=y′= .
特别提醒:
区别 联系
f′(x0) f′(x0)是具体的值,是数值 在x=x0处的导数f′(x0)是导函数f′(x)在x=x0处的函数值,因此求函数在某一点处的导数,一般先求导函数,再计算导函数在这一点的函数值
f′(x) f′(x)是函数f(x)在某区间I上每一点都存在导数而定义的一个新函数,是函数
1.函数在一点处的导数f′(x0)是一个常数.( )
2.函数y=f(x)在点x0处的导数f′(x0)就是导函数f′(x)在点x=x0处的函数值.
( )
3.直线与曲线相切,则直线与已知曲线只有一个公共点.( )
[思考辨析 判断正误]
√
√
×
题型探究
类型一 求切线方程
解 将x=2代入曲线C的方程得y=4,
∴切点P(2,4).
∴k= =4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.
反思与感悟 求曲线在某点处的切线方程的步骤
跟踪训练1 曲线y=x2+1在点P(2,5)处的切线与y轴交点的纵坐标是_____.
-3
∴k= =4.
∴曲线y=x2+1在点(2,5)处的切线方程为y-5=4(x-2),即y=4x-3.
∴切线与y轴交点的纵坐标是-3.
命题角度2 曲线过某点的切线方程
例2 求过点(-1,0)与曲线y=x2+x+1相切的直线方程.
解 设切点为(x0, +x0+1),
解得x0=0或x0=-2.
当x0=0时,切线斜率k=1,过(-1,0)的切线方程为y-0=x+1,
即x-y+1=0.
当x0=-2时,切线斜率k=-3,过(-1,0)的切线方程为y-0=-3(x+1),即3x+y+3=0.
故所求切线方程为x-y+1=0或3x+y+3=0.
反思与感悟 过点(x1,y1)的曲线y=f(x)的切线方程的求法步骤
(1)设切点(x0,f(x0)).
(3)解方程得k=f′(x0),x0,y0,从而写出切线方程.
跟踪训练2 求函数y=f(x)=x3-3x2+x的图象上过原点的切线方程.
∵Δy=f(x0+Δx)-f(x0)
故所求切线方程为x-y=0或5x+4y=0.
类型二 利用图象理解导数的几何意义
例3 已知函数f(x)的图象如图所示,则下列不等关系中正确的是
A.0
f′(2)为函数f(x)的图象在点B(2,f(2))处的切线的斜率,
f′(3)为函数f(x)的图象在点A(3,f(3))处的切线的斜率,
根据图象可知0
跟踪训练3 若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x)在区间[a,b]上的图象可能是
√
解析 依题意,y=f′(x)在[a,b]上是增函数,则在函数f(x)的图象上,各点的切线的斜率随着x的增大而增大,观察四个选项的图象,只有A满足.
例4 已知曲线f(x)=x2-1在x=x0处的切线与曲线g(x)=1-x3在x=x0处的切线互相平行,求x0的值.
类型三 求切点坐标
解 对于曲线f(x)=x2-1,
对于曲线g(x)=1-x3,
引申探究
若将本例条件中的“平行”改为“垂直”,求x0的值.
反思与感悟 求切点坐标的一般步骤
(1)设出切点坐标.
(2)利用导数或斜率公式求出斜率.
(3)利用斜率关系列方程,求出切点的横坐标.
(4)把横坐标代入曲线或切线方程,求出切点纵坐标.
跟踪训练4 直线l:y=x+a(a≠0)和曲线C:f(x)=x3-x2+1相切,则a的
值为____,切点坐标为__________.
解析 设直线l与曲线C的切点为(x0,y0),
又点(x0,f(x0))在直线y=x+a上,将x0=1,y0=1.
代入得a=0,与已知条件矛盾,舍去.
达标检测
1.如果曲线y=f(x)在点(x0,f(x0))处的切线方程为x+2y-3=0,那么
A.f′(x0)>0 B.f′(x0)<0
C.f′(x0)=0 D.f′(x0)不存在
1
2
3
4
5
√
1
2
3
4
5
2.设曲线f(x)=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a等于
√
所以2a=2,所以a=1.
3.已知函数y=f(x)的图象如图所示,则f′(xA)与
f′(xB)的大小关系是
A.f′(xA)>f′(xB)
B.f′(xA)
D.不能确定
解析 由导数的几何意义,知f′(xA),f′(xB)分别是切线在点A,B处切线的斜率,由图象可知f′(xA)
2
3
4
5
√
4.已知曲线y=f(x)=2x2+a在点P处的切线方程为8x-y-15=0,则实数a的值为_____.
1
2
3
4
5
-7
由导数的几何意义可得,
∴x0=2,∴P(2,8+a).
将x=2,y=8+a,代入8x-y-15=0,
得a=-7.
5.已知曲线f(x)=x3在点(a,a3)(a≠0)处的切线与x轴,直线x=a围成的三角形的面积为 ,则a=_____.
±1
∴曲线f(x)=x3在点(a,a3)处的切线斜率为f′(a)=3a2,
∴切线方程为y-a3=3a2(x-a),即y=3a2x-2a3.
1
2
3
4
5
1.导数f′(x0)的几何意义是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,即k=
物理意义是运动物体在某一时刻的瞬时速度.
2.“函数f(x)在点x0处的导数”是一个数值,不是变数,“导函数”是一个函数,二者有本质的区别,但又有密切关系,f′(x0)是其导数y=f′(x)在x=x0处的一个函数值.
3.利用导数求曲线的切线方程,要注意已知点是否在曲线上.如果已知点在曲线上,则以该点为切点的切线方程为y-f(x0)=f′(x0)(x-x0);若已知点不在切线上,则设出切点坐标(x0,f(x0)),表示出切线方程,然后求出切点.
