人教A版(2019)高中数学选择性必修第二册 【整合课件】5.2第1课时 基本初等函数导数 课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.2第1课时 基本初等函数导数 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 09:31:59 | ||
图片预览






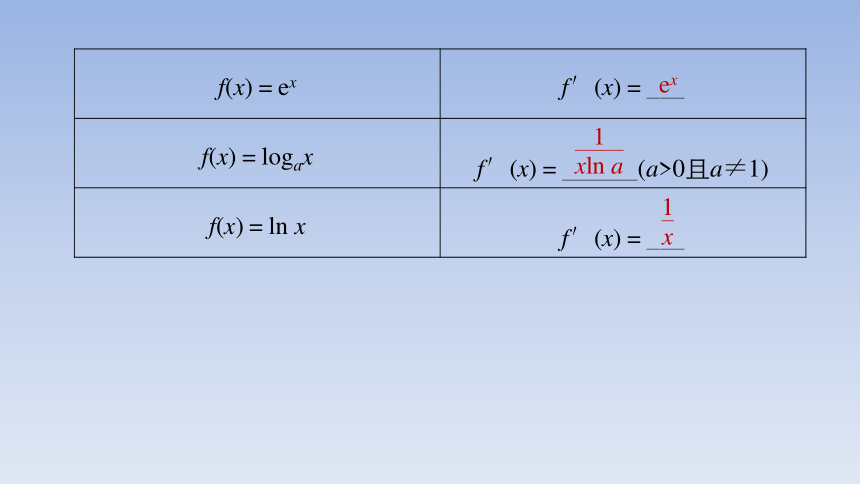


文档简介
(共29张PPT)
第五章 §5.2 导数的计算
第1课时 几个常用函数的导数与基本初等函数的导数公式
学习目标
2.能利用给出的基本初等函数的导数公式求简单函数的导数.
问题导学
达标检测
题型探究
内容索引
问题导学
知识点一 几个常用函数的导数
原函数 导函数
f(x)=c f′(x)=___
f(x)=x f′(x)=___
f(x)=x2 f′(x)=____
f(x)= f′(x)=_____
f(x)= f′(x)=_____
0
1
2x
原函数 导函数
f(x)=c(c为常数) f′(x)=___
f(x)=xα(α∈Q*) f′(x)=______
f(x)=sin x f′(x)=______
f(x)=cos x f′(x)=________
f(x)=ax f′(x)= (a>0)
知识点二 基本初等函数的导数公式
0
αxα-1
cos x
-sin x
axln a
f(x)=ex f′(x)=___
f(x)=logax f′(x)= (a>0且a≠1)
f(x)=ln x f′(x)=___
ex
2.若f′(x)=sin x,则f(x)=cos x.( )
[思考辨析 判断正误]
√
×
×
题型探究
类型一 利用导数公式求函数的导数
例1 求下列函数的导数.
解 y′=0.
(3)y=lg x;
∴y′=(cos x)′=-sin x.
反思与感悟 (1)若所求函数符合导数公式,则直接利用公式求解.
(2)若给出的函数解析式不符合基本初等函数的导数公式,则通过恒等变换对解析式进行化简或变形后求导,如根式要化成指数幂的形式求导.
如y= 可以写成y=x-4,y= 可以写成y= 等,这样就可以直接使用幂函数的求导公式求导,以免在求导过程中出现指数或系数的运算失误.
跟踪训练1 (1)已知函数f(x)= ,则f′(-3)等于
A.81 B.243
C.-243 D.
√
解析 因为f(x)=x-3,
1
解析 因为f(x)=ln x(x>0),
类型二 利用导数公式研究切线问题
命题角度1 求切线方程或切线斜率
y-1=-(x-1),
其与x轴的交点坐标分别为(-1,0),(2,0),
反思与感悟 解决切线问题,关键是确定切点,要充分利用切点处的导数是切线的斜率、切点在切线上及切点在曲线上这三个条件联立方程解决.
跟踪训练2 已知y=kx是曲线y=ln x的一条切线,则k= .
解析 设切点坐标为(x0,y0),
①
又y0=kx0, ②
而且y0=ln x0, ③
命题角度2 求切点坐标问题
例3 求抛物线y=x2上的点到直线x-y-2=0的最短距离.
反思与感悟 利用基本初等函数的求导公式,可求其图象在某一点P(x0,y0)处的切线方程,可以解决一些与距离、面积相关的几何的最值问题,一般都与函数图象的切线有关.解题时可先利用图象分析取最值时的位置情况,再利用导数的几何意义准确计算.
跟踪训练3 已知直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,O是坐标原点,试求与直线l平行的抛物线的切线方程,并在弧 上求一点P,使△ABP的面积最大.
解 由于直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,
∴|AB|为定值,要使△ABP的面积最大,只要点P到AB的距离最大,
设P(x0,y0)为切点,过点P与AB平行的直线斜率k=y′=2x0,
∴k=2x0=2,∴x0=1,y0 =1.
故可得P(1,1),∴切线方程为2x-y-1=0.
故P(1,1)点即为所求弧 上的点,使△ABP的面积最大.
达标检测
1.下列函数求导运算正确的个数为
1
2
3
4
5
A.1 B.2 C.3 D.4
√
解析 ①中(3x)′=3xln 3,②③④均正确.
1
2
3
4
5
2.函数f(x)=x3的斜率等于1的切线有
A.1条 B.2条
C.3条 D.不确定
√
3.已知f(x)=x2,g(x)=ln x,若f′(x)-g′(x)=1,则x= .
1
2
3
4
5
1
4.过原点作曲线y=ex的切线,则切点的坐标为 ,切线的斜率为 .
1
2
3
4
5
(1,e)
解析 设切点坐标为(x0,y0),
切线的斜率为 = ,
e
又y0= , ②
由①②可得x0=1,
∴切点坐标为(1,e),切线的斜率为e.
5.求过曲线y=sin x上一点P 且与在该点处的切线垂直的直线方程.
1
2
3
4
5
1.利用常见函数的导数公式可以比较简捷地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
2.有些函数可先化简再应用公式求导.
-sin x.
3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
第五章 §5.2 导数的计算
第1课时 几个常用函数的导数与基本初等函数的导数公式
学习目标
2.能利用给出的基本初等函数的导数公式求简单函数的导数.
问题导学
达标检测
题型探究
内容索引
问题导学
知识点一 几个常用函数的导数
原函数 导函数
f(x)=c f′(x)=___
f(x)=x f′(x)=___
f(x)=x2 f′(x)=____
f(x)= f′(x)=_____
f(x)= f′(x)=_____
0
1
2x
原函数 导函数
f(x)=c(c为常数) f′(x)=___
f(x)=xα(α∈Q*) f′(x)=______
f(x)=sin x f′(x)=______
f(x)=cos x f′(x)=________
f(x)=ax f′(x)= (a>0)
知识点二 基本初等函数的导数公式
0
αxα-1
cos x
-sin x
axln a
f(x)=ex f′(x)=___
f(x)=logax f′(x)= (a>0且a≠1)
f(x)=ln x f′(x)=___
ex
2.若f′(x)=sin x,则f(x)=cos x.( )
[思考辨析 判断正误]
√
×
×
题型探究
类型一 利用导数公式求函数的导数
例1 求下列函数的导数.
解 y′=0.
(3)y=lg x;
∴y′=(cos x)′=-sin x.
反思与感悟 (1)若所求函数符合导数公式,则直接利用公式求解.
(2)若给出的函数解析式不符合基本初等函数的导数公式,则通过恒等变换对解析式进行化简或变形后求导,如根式要化成指数幂的形式求导.
如y= 可以写成y=x-4,y= 可以写成y= 等,这样就可以直接使用幂函数的求导公式求导,以免在求导过程中出现指数或系数的运算失误.
跟踪训练1 (1)已知函数f(x)= ,则f′(-3)等于
A.81 B.243
C.-243 D.
√
解析 因为f(x)=x-3,
1
解析 因为f(x)=ln x(x>0),
类型二 利用导数公式研究切线问题
命题角度1 求切线方程或切线斜率
y-1=-(x-1),
其与x轴的交点坐标分别为(-1,0),(2,0),
反思与感悟 解决切线问题,关键是确定切点,要充分利用切点处的导数是切线的斜率、切点在切线上及切点在曲线上这三个条件联立方程解决.
跟踪训练2 已知y=kx是曲线y=ln x的一条切线,则k= .
解析 设切点坐标为(x0,y0),
①
又y0=kx0, ②
而且y0=ln x0, ③
命题角度2 求切点坐标问题
例3 求抛物线y=x2上的点到直线x-y-2=0的最短距离.
反思与感悟 利用基本初等函数的求导公式,可求其图象在某一点P(x0,y0)处的切线方程,可以解决一些与距离、面积相关的几何的最值问题,一般都与函数图象的切线有关.解题时可先利用图象分析取最值时的位置情况,再利用导数的几何意义准确计算.
跟踪训练3 已知直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,O是坐标原点,试求与直线l平行的抛物线的切线方程,并在弧 上求一点P,使△ABP的面积最大.
解 由于直线l: 2x-y+4=0与抛物线y=x2相交于A,B两点,
∴|AB|为定值,要使△ABP的面积最大,只要点P到AB的距离最大,
设P(x0,y0)为切点,过点P与AB平行的直线斜率k=y′=2x0,
∴k=2x0=2,∴x0=1,y0 =1.
故可得P(1,1),∴切线方程为2x-y-1=0.
故P(1,1)点即为所求弧 上的点,使△ABP的面积最大.
达标检测
1.下列函数求导运算正确的个数为
1
2
3
4
5
A.1 B.2 C.3 D.4
√
解析 ①中(3x)′=3xln 3,②③④均正确.
1
2
3
4
5
2.函数f(x)=x3的斜率等于1的切线有
A.1条 B.2条
C.3条 D.不确定
√
3.已知f(x)=x2,g(x)=ln x,若f′(x)-g′(x)=1,则x= .
1
2
3
4
5
1
4.过原点作曲线y=ex的切线,则切点的坐标为 ,切线的斜率为 .
1
2
3
4
5
(1,e)
解析 设切点坐标为(x0,y0),
切线的斜率为 = ,
e
又y0= , ②
由①②可得x0=1,
∴切点坐标为(1,e),切线的斜率为e.
5.求过曲线y=sin x上一点P 且与在该点处的切线垂直的直线方程.
1
2
3
4
5
1.利用常见函数的导数公式可以比较简捷地求出函数的导数,其关键是牢记和运用好导数公式.解题时,能认真观察函数的结构特征,积极地进行联想化归.
2.有些函数可先化简再应用公式求导.
-sin x.
3.对于正弦、余弦函数的导数,一是注意函数名称的变化,二是注意函数符号的变化.
