人教A版(2019)高中数学选择性必修第二册 【整合课件】5.2第3课时 复合函数求导数 课件(共32张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 【整合课件】5.2第3课时 复合函数求导数 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 09:32:55 | ||
图片预览








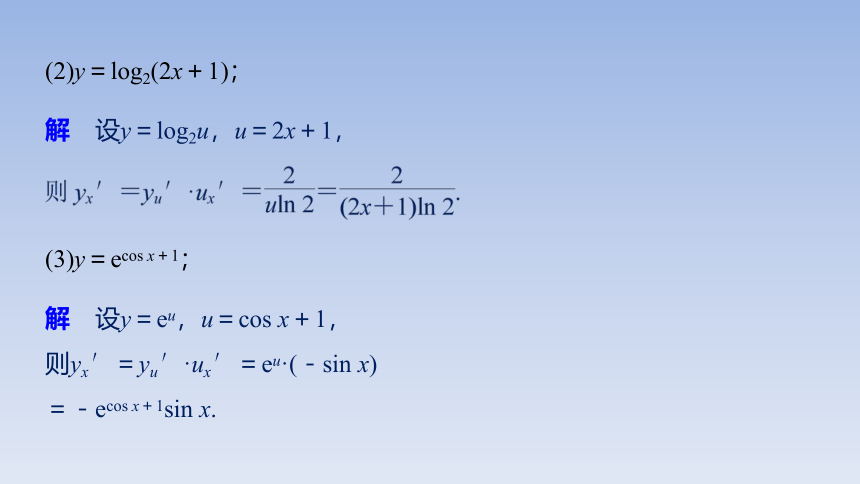
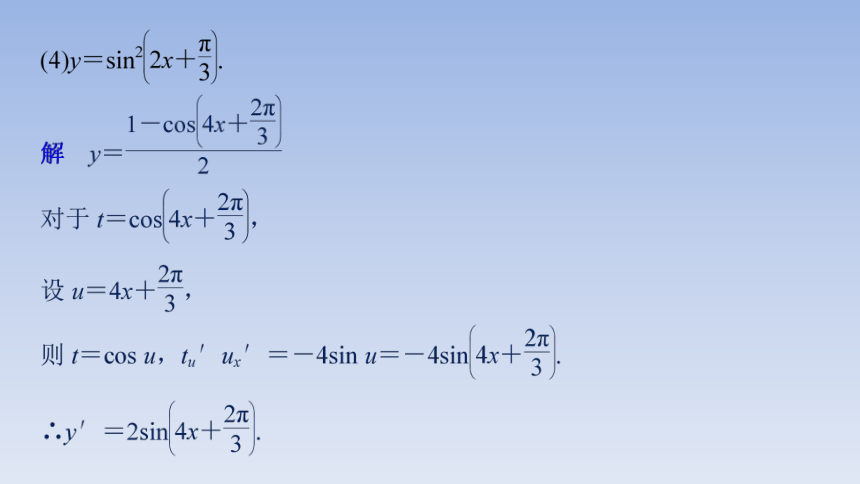

文档简介
(共32张PPT)
第3课时 简单复合函数的导数
学习目标
1.了解复合函数的概念,掌握复合函数的求导法则.
2.能够利用复合函数的求导法则,并结合已经学过的公式、法则进行一些复合函数的求导(仅限于形如f(ax+b)的导数).
问题导学
知识点 复合函数的概念及求导法则
已知函数y=ln(2x+5),y=sin(x+2).
思考 这两个函数有什么共同特征?
答案 函数y=ln(2x+5),y=sin(x+2)都是由两个基本函数复合而成的.
梳理
复合函数的概念 一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成 ,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y= .
复合函数的求导法则 复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为yx′= ,即y对x的导数等于___________
.
x的函数
f(g(x))
yu′·ux′
y对u的导数
与u对x的导数的乘积
1.函数y=e-x的导数为y′=e-x.( )
2.函数f(x)=sin(-x)的导数为f′(x)=cos x.( )
3.函数y=cos(3x+1)由函数y=cos u,u=3x+1复合而成.( )
[思考辨析 判断正误]
√
×
×
题型探究
类型一 求复合函数的导数
命题角度1 单纯的复合函数求导
例1 求下列函数的导数.
解 y=
设y= ,u=1-2x2,
(2)y=log2(2x+1);
解 设y=log2u,u=2x+1,
(3)y=ecos x+1;
解 设y=eu,u=cos x+1,
则yx′=yu′·ux′=eu·(-sin x)
=-ecos x+1sin x.
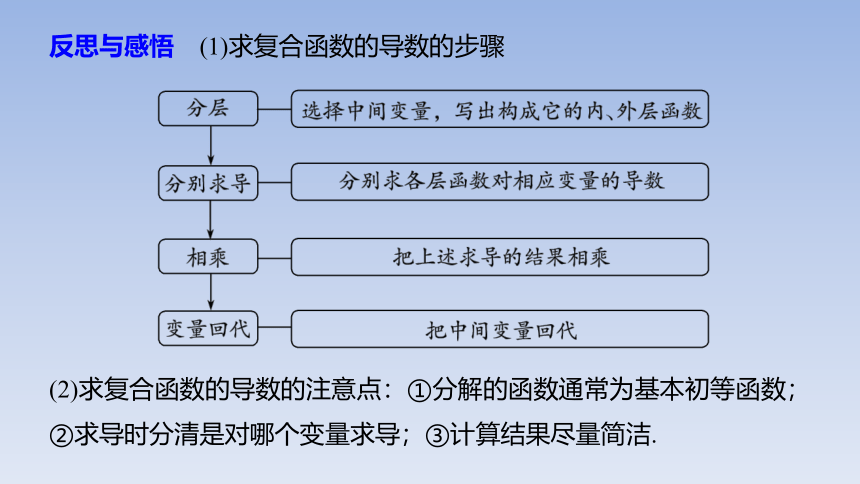
反思与感悟 (1)求复合函数的导数的步骤
(2)求复合函数的导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁.
跟踪训练1 求下列函数的导数.
(1)y=(x2-4)2;
(2)y=ln(6x+4);
解 y′=2(x2-4)(x2-4)′=2(x2-4)·2x
=4x3-16x.
(3)y=103x-2;
解 y′=(103x-2ln 10)·(3x-2)′=3×103x-2ln 10.
(6)y=cos2x.
解 y′=2cos x·(cos x)′=-2cos x·sin x=-sin 2x.
命题角度2 复合函数与导数运算法则结合求导
例2 求下列函数的导数.
反思与感悟 (1)在对函数求导时,应仔细观察及分析函数的结构特征,紧扣求导法则,联系学过的求导公式,对不易用求导法则求导的函数,可适当地进行等价变形,以达到化异求同、化繁为简的目的.
(2)复合函数的求导熟练后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,由外及内逐层求导.
跟踪训练2 求下列函数的导数.
(1)y=sin3x+sin x3;
解 y′=(sin3x+sin x3)′=(sin3x)′+(sin x3)′
=3sin2xcos x+cos x3·3x2
=3sin2xcos x+3x2cos x3.
(2)y=xln(1+2x).
解 y′=x′ln(1+2x)+x[ln(1+2x)]′
类型二 复合函数导数的应用
解 由曲线y=f(x)过(0,0)点,
可得ln 1+1+b=0,故b=-1.
即为曲线y=f(x)在点(0,0)处的切线的斜率.
反思与感悟 复合函数导数的应用问题,正确的求出此函数的导数是前提,审题时注意所给点是不是切点,挖掘题目隐含条件,求出参数,解决已知经过一定点的切线问题,寻求切点是解决问题的关键.
解 由y=esin x,
得y′=(esin x)′=cos xesin x,
即 =1,
则切线方程为y-1=x-0,即x-y+1=0.
若直线l与切线平行,可设直线l的方程为x-y+c=0.
故直线l的方程为x-y+3=0或x-y-1=0.
达标检测
1
2
3
4
5
C.ex-e-x D.ex+e-x
√
√
1
2
3
4
5
1
2
3
4
5
3.已知函数f(x)=ln(3x-1),则f′(1)=_____.
1
2
3
4
5
1
2
3
4
5
-1
解析 由函数y=2cos2x=1+cos 2x,
得y′=(1+cos 2x)′=-2sin 2x,
5.曲线 y= 在点(4,e2)处的切线与坐标轴所围三角形的面积为____.
e2
令x=0,得y=-e2,
令y=0,得x=2,
1
2
3
4
5
解析
求简单复合函数f(ax+b)的导数
实质是运用整体思想,先把简单复合函数转化为常见函数y=f(u),u=ax+b的形式,然后再对y=f(u)与u=ax+b分别求导,并把所得结果相乘.灵活应用整体思想把函数化为y=f(u),u=ax+b的形式是关键.
规律与方法
第3课时 简单复合函数的导数
学习目标
1.了解复合函数的概念,掌握复合函数的求导法则.
2.能够利用复合函数的求导法则,并结合已经学过的公式、法则进行一些复合函数的求导(仅限于形如f(ax+b)的导数).
问题导学
知识点 复合函数的概念及求导法则
已知函数y=ln(2x+5),y=sin(x+2).
思考 这两个函数有什么共同特征?
答案 函数y=ln(2x+5),y=sin(x+2)都是由两个基本函数复合而成的.
梳理
复合函数的概念 一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成 ,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y= .
复合函数的求导法则 复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为yx′= ,即y对x的导数等于___________
.
x的函数
f(g(x))
yu′·ux′
y对u的导数
与u对x的导数的乘积
1.函数y=e-x的导数为y′=e-x.( )
2.函数f(x)=sin(-x)的导数为f′(x)=cos x.( )
3.函数y=cos(3x+1)由函数y=cos u,u=3x+1复合而成.( )
[思考辨析 判断正误]
√
×
×
题型探究
类型一 求复合函数的导数
命题角度1 单纯的复合函数求导
例1 求下列函数的导数.
解 y=
设y= ,u=1-2x2,
(2)y=log2(2x+1);
解 设y=log2u,u=2x+1,
(3)y=ecos x+1;
解 设y=eu,u=cos x+1,
则yx′=yu′·ux′=eu·(-sin x)
=-ecos x+1sin x.
反思与感悟 (1)求复合函数的导数的步骤
(2)求复合函数的导数的注意点:①分解的函数通常为基本初等函数;②求导时分清是对哪个变量求导;③计算结果尽量简洁.
跟踪训练1 求下列函数的导数.
(1)y=(x2-4)2;
(2)y=ln(6x+4);
解 y′=2(x2-4)(x2-4)′=2(x2-4)·2x
=4x3-16x.
(3)y=103x-2;
解 y′=(103x-2ln 10)·(3x-2)′=3×103x-2ln 10.
(6)y=cos2x.
解 y′=2cos x·(cos x)′=-2cos x·sin x=-sin 2x.
命题角度2 复合函数与导数运算法则结合求导
例2 求下列函数的导数.
反思与感悟 (1)在对函数求导时,应仔细观察及分析函数的结构特征,紧扣求导法则,联系学过的求导公式,对不易用求导法则求导的函数,可适当地进行等价变形,以达到化异求同、化繁为简的目的.
(2)复合函数的求导熟练后,中间步骤可以省略,即不必再写出函数的复合过程,直接运用公式,由外及内逐层求导.
跟踪训练2 求下列函数的导数.
(1)y=sin3x+sin x3;
解 y′=(sin3x+sin x3)′=(sin3x)′+(sin x3)′
=3sin2xcos x+cos x3·3x2
=3sin2xcos x+3x2cos x3.
(2)y=xln(1+2x).
解 y′=x′ln(1+2x)+x[ln(1+2x)]′
类型二 复合函数导数的应用
解 由曲线y=f(x)过(0,0)点,
可得ln 1+1+b=0,故b=-1.
即为曲线y=f(x)在点(0,0)处的切线的斜率.
反思与感悟 复合函数导数的应用问题,正确的求出此函数的导数是前提,审题时注意所给点是不是切点,挖掘题目隐含条件,求出参数,解决已知经过一定点的切线问题,寻求切点是解决问题的关键.
解 由y=esin x,
得y′=(esin x)′=cos xesin x,
即 =1,
则切线方程为y-1=x-0,即x-y+1=0.
若直线l与切线平行,可设直线l的方程为x-y+c=0.
故直线l的方程为x-y+3=0或x-y-1=0.
达标检测
1
2
3
4
5
C.ex-e-x D.ex+e-x
√
√
1
2
3
4
5
1
2
3
4
5
3.已知函数f(x)=ln(3x-1),则f′(1)=_____.
1
2
3
4
5
1
2
3
4
5
-1
解析 由函数y=2cos2x=1+cos 2x,
得y′=(1+cos 2x)′=-2sin 2x,
5.曲线 y= 在点(4,e2)处的切线与坐标轴所围三角形的面积为____.
e2
令x=0,得y=-e2,
令y=0,得x=2,
1
2
3
4
5
解析
求简单复合函数f(ax+b)的导数
实质是运用整体思想,先把简单复合函数转化为常见函数y=f(u),u=ax+b的形式,然后再对y=f(u)与u=ax+b分别求导,并把所得结果相乘.灵活应用整体思想把函数化为y=f(u),u=ax+b的形式是关键.
规律与方法
