人教A版(2019)高中数学选择性必修第二册 5.3 《导数在研究函数中的应用---函数的单调性》名师课件(共31张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 5.3 《导数在研究函数中的应用---函数的单调性》名师课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:03:55 | ||
图片预览







文档简介
(共31张PPT)
人教A版同步教材名师课件
---函数的单调性
导数在研究函数中的应用
学习目标
学 习 目 标 核心素养
理解函数的单调性与导数之间的关系 数学抽象
掌握利用导数判断函数的单调性或求函数的单调区间 数学运算
学会利用函数的单调性来求参数或证明不等式等问题 逻辑推理
学习目标
学习目标:
1.理解导数与函数的单调性的关系.
2.掌握利用导数判断函数单调性的方法.
3.会用导数求函数的单调区间.
学科核心素养:
1.通过函数的单调性与其导数正负关系的学习,培养逻辑推理、直观想象的核心素养.
2.借助利用导数研究函数的单调性问题,提升数学运算及逻辑推理的核心素养.
探究新知
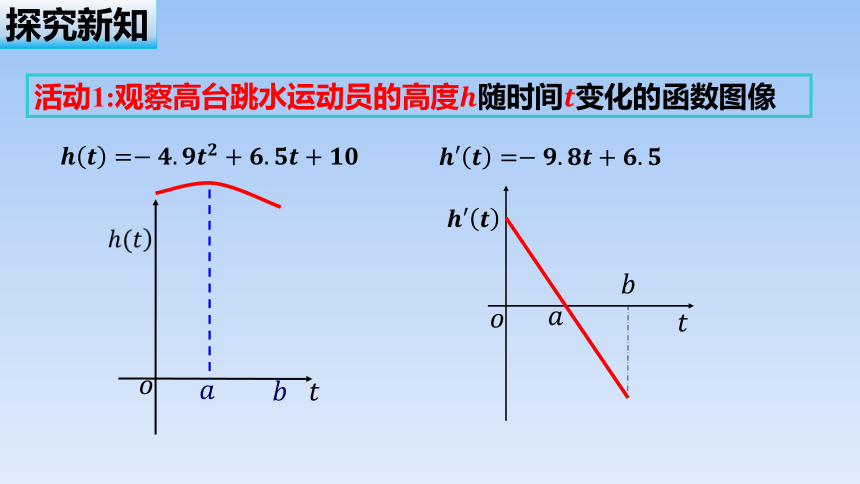
活动1:观察高台跳水运动员的高度随时间变化的函数图像
活动:合作探究
(1)画出函数图象并指出单调性;
(3)观察上述函数的单调性与导函数正负的关系.
(2)求导函数并指出其正负;
(1)
(2)
(3)
(4)
探究新知
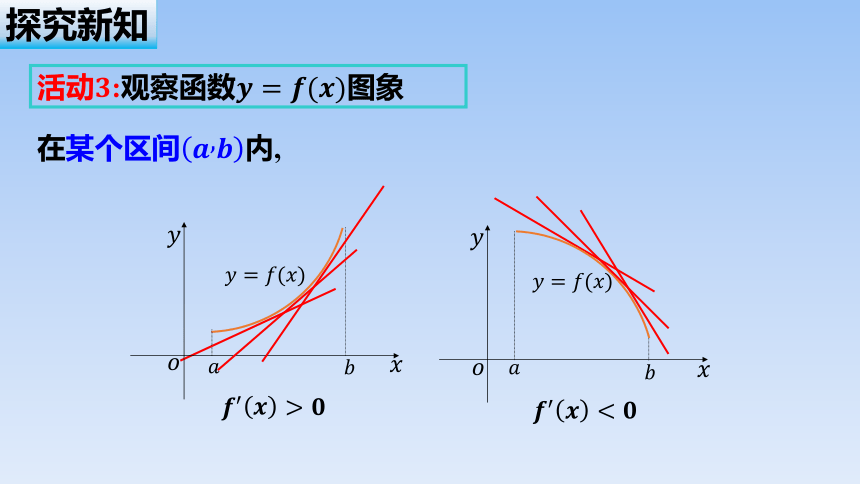
活动:观察函数图象
在某个区间内,
探究新知
函数的单调性与其导函数正负的关系
注意:区间必须是在定义域内的某个区间.
导函数的符号
函数的单调性
探究新知
如果,那么函数在内单调递增;
如果,那么函数在内单调递减.
在某个区间内,
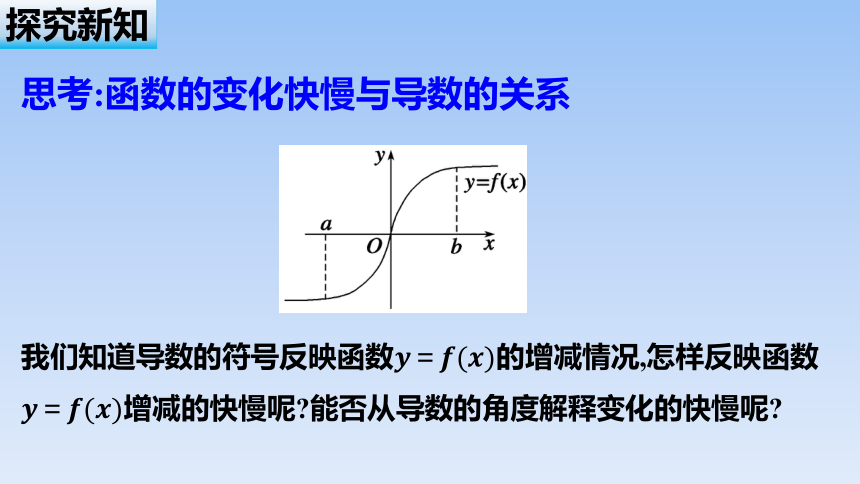
我们知道导数的符号反映函数的增减情况,怎样反映函数增减的快慢呢 能否从导数的角度解释变化的快慢呢
思考:函数的变化快慢与导数的关系
探究新知
探究新知
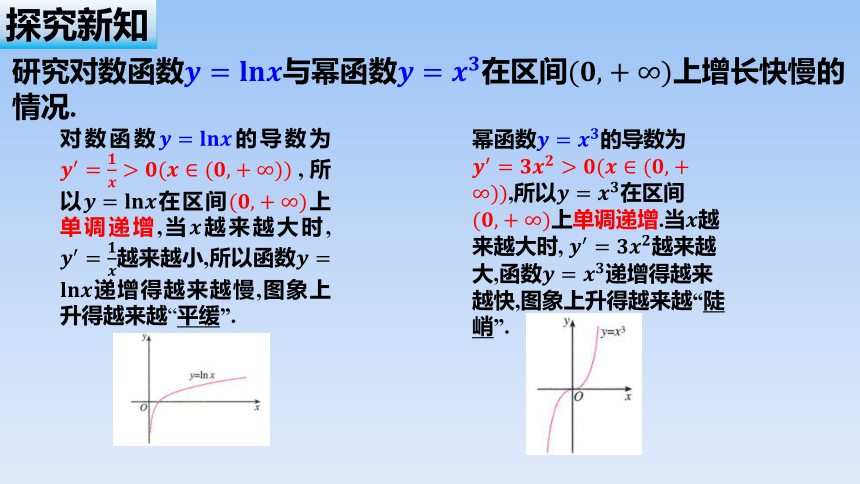
研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为,所以在区间上单调递增,当越来越大时, 越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”.
幂函数的导数为,所以在区间上单调递增.当越来越大时, 越来越大,函数递增得越来越快,图象上升得越来越“陡峭”.
探究新知
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭” (向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
典例讲解
例1、证明:函数在区间上单调递减.
,又,
则,,
所以,
所以,所以在上是减函数.
证明
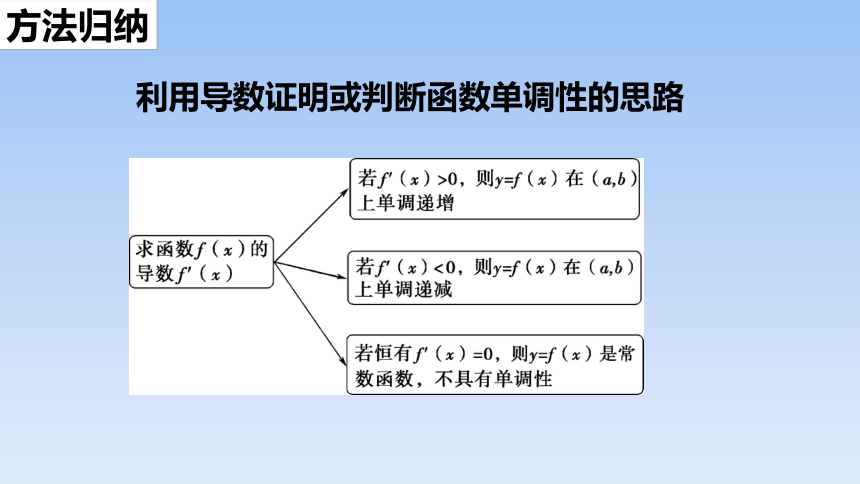
方法归纳
利用导数证明或判断函数单调性的思路
变式训练
1、证明:在上是增函数.
因为,
所以,
当时,
由指数函数的性质知,,
所以,
因此函数在上是增函数.
证明
典例讲解
例2、求下列函数的单调区间.
(1); (2).
(1)函数的定义域为,
因为,所以.
令,解得或.
因此的单调递增区间是,.
令,解得.
因此的单调递减区间是.
解析
典例讲解
例2、求下列函数的单调区间.
(1); (2).
(2)函数的定义域为,其导数为,令,解得;
令,解得,
因此为该函数的单调递增区间,
为该函数的单调递减区间.
解析
(1)确定函数的定义域.
(2)求导数.
(3)在函数的定义域内解不等式和.
(4)根据(3)的结果确定函数的单调区间.
方法归纳
求函数的单调区间的一般步骤
变式训练
2、(1)函数在上的单调递增区间为_____________.
(2)求函数的单调区间.
(1),得,
又,所以.故填.
(2)①当时,,其减区间为,增区间为.②当时,,
或;
.
故的单调递增区间为和,单调递减区间为.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(1)因为,
且在区间上为增函数,
所以在上恒成立,
即在上恒成立,
所以在上恒成立,即.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(2).
①当时,,无减区间,不满足条件.
②当时,令,得;
当时,.
因此在上为减函数.所以,即.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(3)因为,所以,
因为在区间上不单调,
由,得.
所以,
即的取值范围为.
解析
(1)将问题转化为不等式在某区间上的恒成立问题,即(或恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“”时是否满足题意.
(2)先令(或),求出参数的取值范围后,再验证参数取“”时是否满足题意.
方法归纳
利用导数法解决参数取值范围问题的两个基本思路
变式训练
3、已知函数.若在上是增函数,求的取值范围.
由已知条件得.
因为在上是增函数,
所以,即在上恒成立.
而 在上是增函数.
所以所以.
解析
变式训练
3、已知函数.若在上是增函数,求的取值范围.
当时,对有,且仅在时,.
所以时,在上是增函数.
所以的取值范围是.
解析
(1)若在某区间上有有限个点使,其余的点恒有,则仍为增函数(减函数的情形完全类似).
(2)为增函数的充要条件是对任意的都有且在内的任一非空子区间上不恒为.
(3)特别地,在某个区间内如果,那么函数在这个区间内是常数函数.
函数在区间上的导数与单调性的关系
素养提炼
(1)定义域优先的原则:解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)注意“临界点”和“间断点”:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)单调区间的表示:如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
利用导数解决单调性问题需要注意的问题
素养提炼
当堂练习
1.设函数的图象如图所示,则导函数的图象可能为( )
在上是减函数,在上为增函数,
当或时,;
当时,.故选.
解析
当堂练习
2.函数的单调递增区间是( )
A. B. C. D.
,由得,
的单调递增区间为.
3.若函数在区间内单调递减,则实数的取值范围是( )
A. B. C. D.
函数在内单调递减,在内恒成立,即在内恒成立., .
解析
D
解析
C
当堂练习
4.函数的单调递减区间为________.
函数的定义域为,且: ,
求解不等式: ,
结合函数的定义域可得:,
则函数的单调递减区间为.
解析
当堂练习
5.已知函数,讨论的单调性.
的定义域为,
.
①若,则,
所以在上单调递减.
②若,则由,得.
当时,;
当时,.
所以在上单调递减,在上单调递增.
综上,当时,在上单调递减;
当时,在上单调递减,在上单调递增.
解析
1.知识点:函数的单调性与导函数正负的关系.
2.题型与方法:利用导数求函数的单调区间的一般步骤为:
(1)确定函数的定义域;
(2)求导数;
(3)在函数的定义域内解不等式和;
(4)根据(3)的结果确定函数的单调区间.
归纳小结
作 业
P89: 练习:1、2
人教A版同步教材名师课件
---函数的单调性
导数在研究函数中的应用
学习目标
学 习 目 标 核心素养
理解函数的单调性与导数之间的关系 数学抽象
掌握利用导数判断函数的单调性或求函数的单调区间 数学运算
学会利用函数的单调性来求参数或证明不等式等问题 逻辑推理
学习目标
学习目标:
1.理解导数与函数的单调性的关系.
2.掌握利用导数判断函数单调性的方法.
3.会用导数求函数的单调区间.
学科核心素养:
1.通过函数的单调性与其导数正负关系的学习,培养逻辑推理、直观想象的核心素养.
2.借助利用导数研究函数的单调性问题,提升数学运算及逻辑推理的核心素养.
探究新知
活动1:观察高台跳水运动员的高度随时间变化的函数图像
活动:合作探究
(1)画出函数图象并指出单调性;
(3)观察上述函数的单调性与导函数正负的关系.
(2)求导函数并指出其正负;
(1)
(2)
(3)
(4)
探究新知
活动:观察函数图象
在某个区间内,
探究新知
函数的单调性与其导函数正负的关系
注意:区间必须是在定义域内的某个区间.
导函数的符号
函数的单调性
探究新知
如果,那么函数在内单调递增;
如果,那么函数在内单调递减.
在某个区间内,
我们知道导数的符号反映函数的增减情况,怎样反映函数增减的快慢呢 能否从导数的角度解释变化的快慢呢
思考:函数的变化快慢与导数的关系
探究新知
探究新知
研究对数函数与幂函数在区间上增长快慢的情况.
对数函数的导数为,所以在区间上单调递增,当越来越大时, 越来越小,所以函数递增得越来越慢,图象上升得越来越“平缓”.
幂函数的导数为,所以在区间上单调递增.当越来越大时, 越来越大,函数递增得越来越快,图象上升得越来越“陡峭”.
探究新知
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭” (向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
典例讲解
例1、证明:函数在区间上单调递减.
,又,
则,,
所以,
所以,所以在上是减函数.
证明
方法归纳
利用导数证明或判断函数单调性的思路
变式训练
1、证明:在上是增函数.
因为,
所以,
当时,
由指数函数的性质知,,
所以,
因此函数在上是增函数.
证明
典例讲解
例2、求下列函数的单调区间.
(1); (2).
(1)函数的定义域为,
因为,所以.
令,解得或.
因此的单调递增区间是,.
令,解得.
因此的单调递减区间是.
解析
典例讲解
例2、求下列函数的单调区间.
(1); (2).
(2)函数的定义域为,其导数为,令,解得;
令,解得,
因此为该函数的单调递增区间,
为该函数的单调递减区间.
解析
(1)确定函数的定义域.
(2)求导数.
(3)在函数的定义域内解不等式和.
(4)根据(3)的结果确定函数的单调区间.
方法归纳
求函数的单调区间的一般步骤
变式训练
2、(1)函数在上的单调递增区间为_____________.
(2)求函数的单调区间.
(1),得,
又,所以.故填.
(2)①当时,,其减区间为,增区间为.②当时,,
或;
.
故的单调递增区间为和,单调递减区间为.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(1)因为,
且在区间上为增函数,
所以在上恒成立,
即在上恒成立,
所以在上恒成立,即.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(2).
①当时,,无减区间,不满足条件.
②当时,令,得;
当时,.
因此在上为减函数.所以,即.
解析
典例讲解
例3、已知函数.
(1)若在区间内为增函数,求的取值范围.
(2)若的单调递减区间为,求的取值.
(3)若在区间上不单调,求的取值范围.
(3)因为,所以,
因为在区间上不单调,
由,得.
所以,
即的取值范围为.
解析
(1)将问题转化为不等式在某区间上的恒成立问题,即(或恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“”时是否满足题意.
(2)先令(或),求出参数的取值范围后,再验证参数取“”时是否满足题意.
方法归纳
利用导数法解决参数取值范围问题的两个基本思路
变式训练
3、已知函数.若在上是增函数,求的取值范围.
由已知条件得.
因为在上是增函数,
所以,即在上恒成立.
而 在上是增函数.
所以所以.
解析
变式训练
3、已知函数.若在上是增函数,求的取值范围.
当时,对有,且仅在时,.
所以时,在上是增函数.
所以的取值范围是.
解析
(1)若在某区间上有有限个点使,其余的点恒有,则仍为增函数(减函数的情形完全类似).
(2)为增函数的充要条件是对任意的都有且在内的任一非空子区间上不恒为.
(3)特别地,在某个区间内如果,那么函数在这个区间内是常数函数.
函数在区间上的导数与单调性的关系
素养提炼
(1)定义域优先的原则:解决问题的过程只能在定义域内,通过讨论导数的符号来判断函数的单调区间.
(2)注意“临界点”和“间断点”:在对函数划分单调区间时,除了必须确定使导数等于零的点外,还要注意在定义域内的间断点.
(3)单调区间的表示:如果一个函数的单调区间不止一个,这些单调区间之间不能用“∪”连接,而只能用“逗号”或“和”字等隔开.
利用导数解决单调性问题需要注意的问题
素养提炼
当堂练习
1.设函数的图象如图所示,则导函数的图象可能为( )
在上是减函数,在上为增函数,
当或时,;
当时,.故选.
解析
当堂练习
2.函数的单调递增区间是( )
A. B. C. D.
,由得,
的单调递增区间为.
3.若函数在区间内单调递减,则实数的取值范围是( )
A. B. C. D.
函数在内单调递减,在内恒成立,即在内恒成立., .
解析
D
解析
C
当堂练习
4.函数的单调递减区间为________.
函数的定义域为,且: ,
求解不等式: ,
结合函数的定义域可得:,
则函数的单调递减区间为.
解析
当堂练习
5.已知函数,讨论的单调性.
的定义域为,
.
①若,则,
所以在上单调递减.
②若,则由,得.
当时,;
当时,.
所以在上单调递减,在上单调递增.
综上,当时,在上单调递减;
当时,在上单调递减,在上单调递增.
解析
1.知识点:函数的单调性与导函数正负的关系.
2.题型与方法:利用导数求函数的单调区间的一般步骤为:
(1)确定函数的定义域;
(2)求导数;
(3)在函数的定义域内解不等式和;
(4)根据(3)的结果确定函数的单调区间.
归纳小结
作 业
P89: 练习:1、2
