人教A版(2019)高中数学选择性必修第二册 5.3 《导数在研究函数中的应用---函数的极值》名师课件(共25张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 5.3 《导数在研究函数中的应用---函数的极值》名师课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:04:36 | ||
图片预览





文档简介
(共25张PPT)
(1)若在某区间上有有限个点使,其余的点恒有,则仍为增函数(减函数的情形完全类似).
(2)为增函数的充要条件是对任意的都有,且在内的任一非空子区间上不恒为.
(3)特别地,在某个区间内如果,那么函数在这个区间内是常数函数.
函数在区间上的导数与单调性的关系
复习引入
人教A版同步教材名师课件
---函数的极值
导数在研究函数中的应用
学习目标
学 习 目 标 核心素养
理解函数的极值的概念及它与导数的关系 逻辑推理
掌握利用导数求函数的极值 数学运算
学会利用极值来研究函数的其他性质 数学建模
学习目标
学习目标:
1.了解极大值、极小值的概念.
2.了解函数在某点取得极值的必要条件和充分条件.
3.会用导数求函数的极大值、极小值.
学科核心素养:
1.通过极值点与极值概念的学习,体现了数学抽象的核心素养.
2.借助函数极值的求法,提升学生的逻辑推理、数学运算的核心素养.
探究新知
探究新知
o
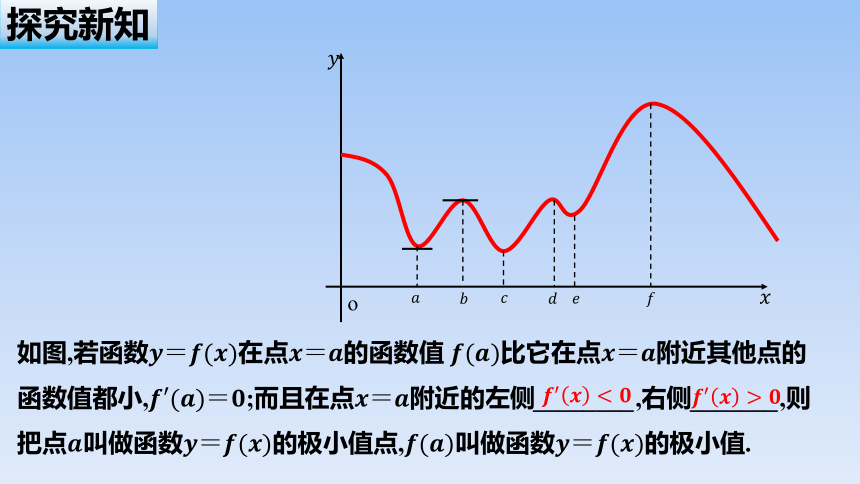
如图,若函数在点的函数值 比它在点附近其他点的函数值都小,;而且在点附近的左侧________,右侧_______,则把点叫做函数的极小值点,叫做函数的极小值.
探究新知
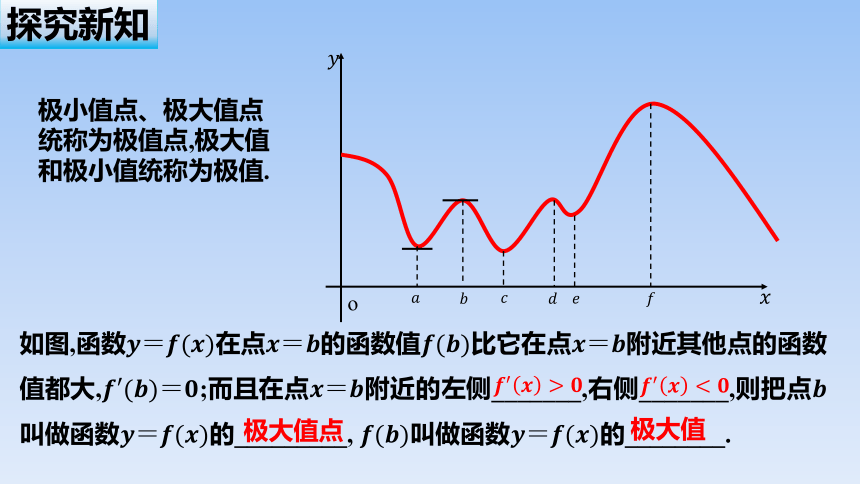
如图,函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧_______,右侧_______,则把点叫做函数的_________, 叫做函数的________.
极大值点
极大值
极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
o
探究新知
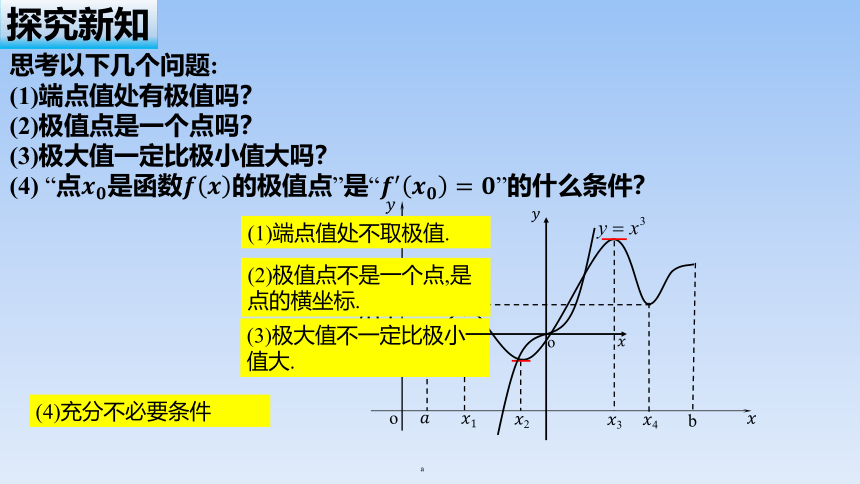
思考以下几个问题:
(1)端点值处有极值吗?
(2)极值点是一个点吗?
(3)极大值一定比极小值大吗?
(4) “点是函数的极值点”是“”的什么条件?
o
2
3
4
b
a
(1)端点值处不取极值.
(3)极大值不一定比极小值大.
(2)极值点不是一个点,是点的横坐标.
(4)充分不必要条件
o
探究新知
下图是导函数的图象,试根据导函数图象找出函数的极值点,并指出哪些是极大值点,哪些是极小值点.
O
探究新知
是函数的极小值点.
和是函数的极值点,
是函数的极大值点,
列表如下:
例1、求函数的极值.
典例讲解
当时,有极大值 ;
当时,有极小值.
由, .则或.
令则或;
令则.
解析
单调递增
单调递减
单调递增
(1)求导数;
(2)求方程的全部实根;
(3)列表,检查在方程的根左、右两侧的值的符号;
(4)判断单调性,确定极值.
求函数极值的步骤
方法归纳
1、求函数的极值点和极值
单调递减 极小值 单调递增
变式训练
.
令可得即.
令可得即.
令可得即.
故该函数有极小值,极小值点为,无极大值.
解析
典例讲解
例2、已知函数,在点处的极小值为.
(1)确定,的值,并求的单调区间.
(1)导函数为,
由已知可得,即
解得,故,
令,则或,令,则或,
令,则,
的单增区间是和,单减区间为.
解析
0 0
单增 极大值 单减 极小值 单增
典例讲解
故可得.
(3)的取值范围是.
例2、已知函数,在点处的极小值为.
(2)若函数的图象与函数的图象恰好有三个不同的交点,求实数的取值范围.
(3)若(2)中的“恰好三个交点”改为“恰好一个交点”求实数的取值范围.
(2)由(1)可得下表
解析
根据极值点处导数为和极值这两个条件列方程组,利用待定系数法求解.
因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
方法归纳
已知函数极值点或极值求参数的策略
变式训练
2、已知函数,当时函数取得极值,若函数只有三个零点,求实数的取值范围.
由已知, 可得.
故, .
令得或.
令得或.
在和上单增,在上单减.
可得函数的极大值为,极小值为
即.
解析
(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧区域而言的.极值点是区间内部的点而不会是端点.
(2)若在某区间内有极值,那么在该区间内一定不是单调函数,即在区间上单调的函数没有极值.
(3)在定义域的某个区间内极大值或极小值并不唯一,也可能不存在极值.
(4)函数的极值点是指函数取得极值时对应点的横坐标,而不是点;极值是函数在极值点处取得的函数值,即函数取得极值时对应点的纵坐标.
对极值的再认识
素养提炼
(1)可导函数的极值点是导数为零的点,但是导数为零的点不一定是极值点,即“点是可导函数的极值点”是“”的充分不必要条件.
(2)可导函数在点处取得极值的充要条件是,且在左侧和右侧的符号不同.
(3)如果在的两侧的符号相同,则不是的极值点.
素养提炼
极值点与导数为零的关系
当堂练习
1.函数的定义域为,它的导函数的部分图象如图所示,则下面结论错误的是( )
由题图可知,当时,,
当时,,当时,,
是函数的极大值点,
是函数的极小值点,故A,B,C正确,D错误.
A.在上函数为增函数
B.在上函数为减函数
C.在上函数有极大值
D.是函数在区间上的极小值点
解析
D
当堂练习
2.设函数,则( )
A.为的极大值点
B.为的极小值点
C.为的极大值点
D.为的极小值点
令,得.
当时,;当时,.
故当时,取得极小值.
解析
D
当堂练习
3.已知函数既有极大值又有极小值,则实数的取值范围是____________.
,
函数既有极大值又有极小值,
方程有两个不相等的实根,
,
即,解得或.
解析
当堂练习
4.已知函数,则函数的极大值为______.
,故,
解得,
所以, .
由得,得.
所以函数在单调递增,在单调递减,
故的极大值为.
解析
归纳小结
1.若函数在区间内有极值,那么在内绝不是单调函数,即在某区间上单调函数没有极值.
2.已知函数的极值情况,逆向应用确定函数的解析式,研究函数性质时,需注意两点:
(1)常根据极值点处导数为和极值两个条件列方程组,利用待定系数法求解.
(2)因为函数在一点的导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证极值点的合理性.
作 业
P92 练习:1、2
(1)若在某区间上有有限个点使,其余的点恒有,则仍为增函数(减函数的情形完全类似).
(2)为增函数的充要条件是对任意的都有,且在内的任一非空子区间上不恒为.
(3)特别地,在某个区间内如果,那么函数在这个区间内是常数函数.
函数在区间上的导数与单调性的关系
复习引入
人教A版同步教材名师课件
---函数的极值
导数在研究函数中的应用
学习目标
学 习 目 标 核心素养
理解函数的极值的概念及它与导数的关系 逻辑推理
掌握利用导数求函数的极值 数学运算
学会利用极值来研究函数的其他性质 数学建模
学习目标
学习目标:
1.了解极大值、极小值的概念.
2.了解函数在某点取得极值的必要条件和充分条件.
3.会用导数求函数的极大值、极小值.
学科核心素养:
1.通过极值点与极值概念的学习,体现了数学抽象的核心素养.
2.借助函数极值的求法,提升学生的逻辑推理、数学运算的核心素养.
探究新知
探究新知
o
如图,若函数在点的函数值 比它在点附近其他点的函数值都小,;而且在点附近的左侧________,右侧_______,则把点叫做函数的极小值点,叫做函数的极小值.
探究新知
如图,函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧_______,右侧_______,则把点叫做函数的_________, 叫做函数的________.
极大值点
极大值
极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
o
探究新知
思考以下几个问题:
(1)端点值处有极值吗?
(2)极值点是一个点吗?
(3)极大值一定比极小值大吗?
(4) “点是函数的极值点”是“”的什么条件?
o
2
3
4
b
a
(1)端点值处不取极值.
(3)极大值不一定比极小值大.
(2)极值点不是一个点,是点的横坐标.
(4)充分不必要条件
o
探究新知
下图是导函数的图象,试根据导函数图象找出函数的极值点,并指出哪些是极大值点,哪些是极小值点.
O
探究新知
是函数的极小值点.
和是函数的极值点,
是函数的极大值点,
列表如下:
例1、求函数的极值.
典例讲解
当时,有极大值 ;
当时,有极小值.
由, .则或.
令则或;
令则.
解析
单调递增
单调递减
单调递增
(1)求导数;
(2)求方程的全部实根;
(3)列表,检查在方程的根左、右两侧的值的符号;
(4)判断单调性,确定极值.
求函数极值的步骤
方法归纳
1、求函数的极值点和极值
单调递减 极小值 单调递增
变式训练
.
令可得即.
令可得即.
令可得即.
故该函数有极小值,极小值点为,无极大值.
解析
典例讲解
例2、已知函数,在点处的极小值为.
(1)确定,的值,并求的单调区间.
(1)导函数为,
由已知可得,即
解得,故,
令,则或,令,则或,
令,则,
的单增区间是和,单减区间为.
解析
0 0
单增 极大值 单减 极小值 单增
典例讲解
故可得.
(3)的取值范围是.
例2、已知函数,在点处的极小值为.
(2)若函数的图象与函数的图象恰好有三个不同的交点,求实数的取值范围.
(3)若(2)中的“恰好三个交点”改为“恰好一个交点”求实数的取值范围.
(2)由(1)可得下表
解析
根据极值点处导数为和极值这两个条件列方程组,利用待定系数法求解.
因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.
方法归纳
已知函数极值点或极值求参数的策略
变式训练
2、已知函数,当时函数取得极值,若函数只有三个零点,求实数的取值范围.
由已知, 可得.
故, .
令得或.
令得或.
在和上单增,在上单减.
可得函数的极大值为,极小值为
即.
解析
(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧区域而言的.极值点是区间内部的点而不会是端点.
(2)若在某区间内有极值,那么在该区间内一定不是单调函数,即在区间上单调的函数没有极值.
(3)在定义域的某个区间内极大值或极小值并不唯一,也可能不存在极值.
(4)函数的极值点是指函数取得极值时对应点的横坐标,而不是点;极值是函数在极值点处取得的函数值,即函数取得极值时对应点的纵坐标.
对极值的再认识
素养提炼
(1)可导函数的极值点是导数为零的点,但是导数为零的点不一定是极值点,即“点是可导函数的极值点”是“”的充分不必要条件.
(2)可导函数在点处取得极值的充要条件是,且在左侧和右侧的符号不同.
(3)如果在的两侧的符号相同,则不是的极值点.
素养提炼
极值点与导数为零的关系
当堂练习
1.函数的定义域为,它的导函数的部分图象如图所示,则下面结论错误的是( )
由题图可知,当时,,
当时,,当时,,
是函数的极大值点,
是函数的极小值点,故A,B,C正确,D错误.
A.在上函数为增函数
B.在上函数为减函数
C.在上函数有极大值
D.是函数在区间上的极小值点
解析
D
当堂练习
2.设函数,则( )
A.为的极大值点
B.为的极小值点
C.为的极大值点
D.为的极小值点
令,得.
当时,;当时,.
故当时,取得极小值.
解析
D
当堂练习
3.已知函数既有极大值又有极小值,则实数的取值范围是____________.
,
函数既有极大值又有极小值,
方程有两个不相等的实根,
,
即,解得或.
解析
当堂练习
4.已知函数,则函数的极大值为______.
,故,
解得,
所以, .
由得,得.
所以函数在单调递增,在单调递减,
故的极大值为.
解析
归纳小结
1.若函数在区间内有极值,那么在内绝不是单调函数,即在某区间上单调函数没有极值.
2.已知函数的极值情况,逆向应用确定函数的解析式,研究函数性质时,需注意两点:
(1)常根据极值点处导数为和极值两个条件列方程组,利用待定系数法求解.
(2)因为函数在一点的导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证极值点的合理性.
作 业
P92 练习:1、2
