人教A版(2019)高中数学选择性必修第二册 5.3.2《函数的极值与导数》链接高考课件(共17张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第二册 5.3.2《函数的极值与导数》链接高考课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-03 14:05:26 | ||
图片预览






文档简介
(共17张PPT)
人教A版同步教材名师课件
函数的极值与导数
从高考考查情况来看,利用导数研究函数的极值:①直接考查确定函数的极值;②利用极值求参数.主要以解答题的形式考查,也可能以客观题的形式出现,难度中高档.
考情分析
考点
利用极值确定函数图象
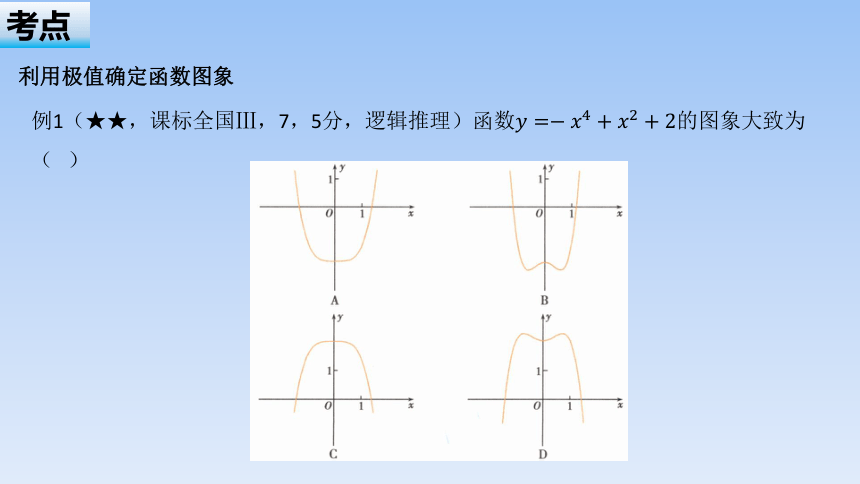
例1(★★,课标全国Ⅲ,7,5分,逻辑推理)函数的图象大致为( )
解法一: 令 ,则 ,当或 时,递增;当 或时,递减.由此可得的图象大致为D中的图象.故选D.
解法二:令 ,则 ,易知 有3个极值点,排除A,C.由=2 ,排除B.故选D.
答案 D
解析
主编点评
本题主要考查函数图象的识辨,解决函数图象的识辨问题,通常利用排除法.根据函数的定义域、值域、单调性、周期性、奇偶性、对称性、特殊值等来识辨.
例2(★★,课标全国Ⅱ,21节选,4分,数学运算)已知函数 .证明:存在唯一的极值点.
证明 的定义域为 .
因为单调递增,
单调递减,所以单调递增.
又 ,
故存在唯一,使得 .
又当时,单调递减;当时,单调递增.
因此,存在唯一的极值点.
例3(★★,天津,20节选,8分,逻辑推理)设函数,其中 ,且 , 是公差为d的等差数列.
(1)若 ,求曲线在点处的切线方程;
(2)若,求的极值.
思路分析 (1)先求得 ,再用点斜式求切线方程;(2) 有两零点 ,大小确定可直接列表求极值.
(1)由已知,可得 ,故 .因此,又因为曲线在点处的切线方程为,故所求切线方程为 .
解析
(2)由已知可得
.
令 ,解得 ,或.
当变化时,的变化情况如下表:
x
+ 0 - 0 +
极大值 极小值
所以函数的极大值为 ;
函数的极小值为 .
主编点评
本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法.考查函数思想,考查综合分析问题和解决问题的能力.
例4(★★,北京,18,13分,逻辑推理)设函数 .
(1)若曲线在点 处的切线与轴平行,求;
(2)若在2处取得极小值,求的取值范围.
思路分析 (1)切线与轴平行,故 ,即=0 ,从而列方程求 .
(2) 中所含参数对函数的单调性有影响,因此需按的取值分类讨论,再确定的极值.
解析
(1)函数的定义域为,+ =
若函数在处的切线与轴平行,则,即 .
(2)由(1)可知 .
(i)当时,令0 ,得 ,
的变化情况如下表:
x 2
+ 0 -
极大值
不满足题意;
(ii)当时,令=0 ,得 或 ,
①当 ,即 时,的变化情况如下表:
x 2
- 0 + 0 -
极小值 极大值
不满足题意;
②当 时,
当 ,即 时, ,函数无极值点;
当 ,即 时,的变化情况如下表:
x 2
+ 0 - 0 +
极大值 极小值
满足题意;
当2 ,即 时,的变化情况如下表:
x
+ 0 - 0 +
极大值 极小值
不满足题意.综上所述,的取值范围是 .
主编点评
本题主要考查导数的运算、导数的几何意义,运用导数研究函数的极值.注意分类讨论思想及逻辑推理素养的应用.
自主招生
例5(★★,清华大学能力测试题,直观想象)已知函数则( )
A.若有两个极值点,则 或
B.若有极小值点,则
C.若有极大值点,则
D.使连续的有3个取值
作出函数和的图象,如图所示.对于选项A ,若有两个极值点,则或 ,选项A错误;对于选项B ,当时,是函数的极小值点,所以选项B错误;选项C正确;对于选项D ,使连续的有3个取值: ,所以选项D正确.
答案 CD、
主编点评
本题主要考查导数的运算及利用导数研究函数的性质,注意直观想象素养的应用.
解析
例6(★★,华约联盟自主招生节选,逻辑推理)已知函数 .求证:函数的区间上存在唯一的极值点,并用二分法求函数取得极值时相应的近似值.(误差不超过0.2 ,参考数据: )
思路分析 先求导得 ,将 存在唯一极值点.转化为有唯一零点,进而借助二分法求值.
解析
ee,所以 ,
设 ,
故在区间 上单调递增,在区间上有唯一的零点.
所以在区间上有唯一的极小值点.
①,而 ,所以极值点在区间 上;
②,所以极值点在区间 上;
③ ,所以区间 上任意一点即为所求.
故可选取作为函数取得极值时相应x的近似值.
主编点评
本题主要考查导数的运算及利用导数研究函数的性质,函数的零点及二分法的应用,注意逻辑推理素养的应用.
人教A版同步教材名师课件
函数的极值与导数
从高考考查情况来看,利用导数研究函数的极值:①直接考查确定函数的极值;②利用极值求参数.主要以解答题的形式考查,也可能以客观题的形式出现,难度中高档.
考情分析
考点
利用极值确定函数图象
例1(★★,课标全国Ⅲ,7,5分,逻辑推理)函数的图象大致为( )
解法一: 令 ,则 ,当或 时,递增;当 或时,递减.由此可得的图象大致为D中的图象.故选D.
解法二:令 ,则 ,易知 有3个极值点,排除A,C.由=2 ,排除B.故选D.
答案 D
解析
主编点评
本题主要考查函数图象的识辨,解决函数图象的识辨问题,通常利用排除法.根据函数的定义域、值域、单调性、周期性、奇偶性、对称性、特殊值等来识辨.
例2(★★,课标全国Ⅱ,21节选,4分,数学运算)已知函数 .证明:存在唯一的极值点.
证明 的定义域为 .
因为单调递增,
单调递减,所以单调递增.
又 ,
故存在唯一,使得 .
又当时,单调递减;当时,单调递增.
因此,存在唯一的极值点.
例3(★★,天津,20节选,8分,逻辑推理)设函数,其中 ,且 , 是公差为d的等差数列.
(1)若 ,求曲线在点处的切线方程;
(2)若,求的极值.
思路分析 (1)先求得 ,再用点斜式求切线方程;(2) 有两零点 ,大小确定可直接列表求极值.
(1)由已知,可得 ,故 .因此,又因为曲线在点处的切线方程为,故所求切线方程为 .
解析
(2)由已知可得
.
令 ,解得 ,或.
当变化时,的变化情况如下表:
x
+ 0 - 0 +
极大值 极小值
所以函数的极大值为 ;
函数的极小值为 .
主编点评
本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法.考查函数思想,考查综合分析问题和解决问题的能力.
例4(★★,北京,18,13分,逻辑推理)设函数 .
(1)若曲线在点 处的切线与轴平行,求;
(2)若在2处取得极小值,求的取值范围.
思路分析 (1)切线与轴平行,故 ,即=0 ,从而列方程求 .
(2) 中所含参数对函数的单调性有影响,因此需按的取值分类讨论,再确定的极值.
解析
(1)函数的定义域为,+ =
若函数在处的切线与轴平行,则,即 .
(2)由(1)可知 .
(i)当时,令0 ,得 ,
的变化情况如下表:
x 2
+ 0 -
极大值
不满足题意;
(ii)当时,令=0 ,得 或 ,
①当 ,即 时,的变化情况如下表:
x 2
- 0 + 0 -
极小值 极大值
不满足题意;
②当 时,
当 ,即 时, ,函数无极值点;
当 ,即 时,的变化情况如下表:
x 2
+ 0 - 0 +
极大值 极小值
满足题意;
当2 ,即 时,的变化情况如下表:
x
+ 0 - 0 +
极大值 极小值
不满足题意.综上所述,的取值范围是 .
主编点评
本题主要考查导数的运算、导数的几何意义,运用导数研究函数的极值.注意分类讨论思想及逻辑推理素养的应用.
自主招生
例5(★★,清华大学能力测试题,直观想象)已知函数则( )
A.若有两个极值点,则 或
B.若有极小值点,则
C.若有极大值点,则
D.使连续的有3个取值
作出函数和的图象,如图所示.对于选项A ,若有两个极值点,则或 ,选项A错误;对于选项B ,当时,是函数的极小值点,所以选项B错误;选项C正确;对于选项D ,使连续的有3个取值: ,所以选项D正确.
答案 CD、
主编点评
本题主要考查导数的运算及利用导数研究函数的性质,注意直观想象素养的应用.
解析
例6(★★,华约联盟自主招生节选,逻辑推理)已知函数 .求证:函数的区间上存在唯一的极值点,并用二分法求函数取得极值时相应的近似值.(误差不超过0.2 ,参考数据: )
思路分析 先求导得 ,将 存在唯一极值点.转化为有唯一零点,进而借助二分法求值.
解析
ee,所以 ,
设 ,
故在区间 上单调递增,在区间上有唯一的零点.
所以在区间上有唯一的极小值点.
①,而 ,所以极值点在区间 上;
②,所以极值点在区间 上;
③ ,所以区间 上任意一点即为所求.
故可选取作为函数取得极值时相应x的近似值.
主编点评
本题主要考查导数的运算及利用导数研究函数的性质,函数的零点及二分法的应用,注意逻辑推理素养的应用.
